
A Genetic Algorithm for Training Recognizers of Latent Abnormal
Behavior of Dynamic Systems
Victor Shcherbinin and Valery Kostenko
Department of Computational Mathematics and Cybernetics, Moscow State University, Moscow, Russia
Keywords:
Genetic Algorithm, Clustering, Machine Learning, Supervised Learning, Unsupervised Learning, Dynamic
System, Abnormal Behavior, Training Set, Algebraic Approach, Axiomatic Approach.
Abstract:
We consider the problem of automatic construction of algorithms for recognition of abnormal behavior seg-
ments in phase trajectories of dynamic systems. The recognition algorithm is trained on a set of trajectories
containing normal and abnormal behavior of the system. The exact position of segments corresponding to ab-
normal behavior in the trajectories of the training set is unknown. To construct recognition algorithm, we use
axiomatic approach to abnormal behavior recognition. In this paper we propose a novel two-stage training al-
gorithm which uses ideas of unsupervised learning and evolutonary computation. The results of experimental
evaluation of the proposed algorithm and its variations on synthetic data show statistically significant increase
in recognition quality for the recognizers constructed by the proposed algorithm compared to the existing
training algorithm.
1 INTRODUCTION
Consider a dynamic system information about which
can be accessed by reading data from sensors sur-
rounding the system. The sensor readings are ob-
tained from the sensors with a fixed frequency 1/τ.
A multidimensional phase trajectory in the space
of sensor readings is an ordered set of vectors X =
(x
1
, x
2
, ..., x
k
), where x
i
∈ R
s
is a vector of sensor
readings at t = t
0
+ i · τ.
We assume that at any given moment of time the
system can be in one of three states:
• Normal state. In this state, the system is fully
functional.
• Abnormal state. In this state, the system is not
fully functional or is going to lose some of its
functions soon.
• Emergency state. In this state, the system is not
functional.
The behavior that the system exhibits when it is in
an abnormal state is called abnormal behavior. We
assume that there are L classes of abnormal behavior,
each of these classes is characterized by a phase tra-
jectory X
l
Anom
called a reference trajectory.
We assume that some period of time after exhibit-
ing abnormal behavior of class l, the system enters
an emergency state of class l. Our goal is to predict
the emergency state of the system by recognizing the
abnormal behavior that precedes it.
The observed phase trajectory X of the system can
contain segments of abnormal behavior which are dis-
torted compared to the reference trajectories. The dis-
tortions can be classified as amplitude distortions and
time distortions. We say that a segment of abnormal
behavior is distorted by amplitude compared to a ref-
erence trajectory if values in some points of the seg-
ment differ from those in the corresponding points of
the reference trajectory. We say that a segment of ab-
normal behavior is distorted by time compared to a
reference trajectory if there are missing or extra points
in the segment compared to the reference trajectory.
An example of an amplitude distortion is a stationary
noise.
We need to recognize abnormal behavior of the
system by finding abnormal behavior segments in the
observed trajectory of the system and abnormal be-
havior class number for each segment found.
There are various problem settings that deal with
recognition of abnormal behavior of dynamic sys-
tems. For example, (Yairi et al., 2001) considers
recognition of anomalies in time series of house-
keeping data of spacecraft systems. The problem set-
ting in this paper differs from our paper: the authors
build a model (a set of rules) for normal behavior of
the system and consider any behavior deviating from
358
Shcherbinin, V. and Kostenko, V..
A Genetic Algorithm for Training Recognizers of Latent Abnor mal Behavior of Dynamic Systems.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 358-365
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
this model abnormal. In our paper, we look for spe-
cific patterns of abnormal behavior in the observed
trajectory of the dynamic system.
A variety of methods are used in the pattern recog-
nition field, including the methods based on artificial
neural networks (Haykin, 1998), k-nearest neighbor
algorithm (Cover and Hart, 1967), algorithms based
on Singular Spectrum Analysis (Hassani, 2007) and
others. However, application of these methods and
algorithms to this particular problem is complicated
because of the presence of non-linear amplitude and
time distortions of abnormal behavior segments in the
observed phase trajectory X. To overcome these dif-
ficulties (emerging from the properties of dynamic
systems in question) a parametric family of recogni-
tion algorithms based on axiomatic approach to ab-
normal behavior recognition was introduced in (Ko-
valenko et al., 2005). The idea of this parametric fam-
ily is based on the idea of using algebraic approach
to label planar configurations described in (Rudakov
and Chekhovich, 2003). A genetic training algo-
rithm for the parametric family was suggested in (Ko-
valenko et al., 2010) and improved in (Shcherbinin
and Kostenko, 2013). Results from (Kostenko and
Shcherbinin, 2013) show that this parametric fam-
ily of recognition algorithms demonstrates high tol-
erance to non-linear amplitude and time distortions of
abnormal behavior segments compared to other ap-
proaches.
The methods described above are developed for
the case when the reference abnormal behavior trajec-
tory is known and we need to find it in the observed
trajectory, taking into account possible amplitude and
time distortions. In this paper we consider a more
difficult problem, when the exact position of the ab-
normal behavior trajectories in the training set is not
known. We only know the points of time when the
system exhibited emergency state. We assume that the
training set consists of trajectories of normal behavior
and trajectories which contain segments of abnormal
behavior, while the exact position of these segments is
not known. We call the problem of recognizing such
abnormal behavior latent abnormal behavior recog-
nition problem.
For this problem a directed search algorithm for
training recognizers based on axiomatic approach was
proposed in (Kostenko and Shcherbinin, 2013). This
paper introduces a new algorithm for training recog-
nizers based on axiomatic approach. The proposed
algorithm uses ideas of unsupervised learning and ge-
netic algorithms.
2 LATENT ABNORMAL
BEHAVIOR RECOGNITION
We assume that we always know if the system is in
an emergency state, but it is not immediately obvious
(without analyzing the trajectory of the system) if the
system is in normal or abnormal state. That means
that when the training dataset containing examples of
the trajectories is formed, we can’t label the positions
of the segments of abnormal behavior. We can only
label the points where the system is in an emergency
state, i. e. the points of emergency.
We assume that our dataset T S has the following
structure.
• For each class l of abnormal behavior, T S includes
trajectories which contain exactly one segment of
abnormal behavior of class l and no segments of
abnormal behavior of other classes. Such trajecto-
ries are called emergency trajectories, since they
can be acquired by taking a segment of a system’s
trajectory that lies directly before the emergency
point.
• T S also includes trajectories which contain no
segments of abnormal behavior, i.e. where the
system exhibits only normal behavior. We call
these trajectories normal trajectories.
The problem of constructing a dataset with such
structure (i. e. ensuring that the emergency trajecto-
ries contain exactly one segment of abnormal behav-
ior and the normal trajectories contain no segments of
abnormal behavior) is a separate problem which we
don’t consider in this paper.
The dataset T S is divided into two non-
overlapping parts: the training set
f
T S and the vali-
dation set
c
T S. The training set
f
T S and the validation
set
c
T S have the same size and contain emergency tra-
jectories for each class of abnormal behavior as well
as normal trajectories.
Suppose we are given an objective function
ϕ(e
1
, e
2
) : Z
+
× Z
+
→ R
+
which is non-decreasing
w.r.t. both its arguments. The problem of auto-
matic construction of latent abnormal behavior recog-
nition algorithm is formulated as follows (Kostenko
and Shcherbinin, 2013). Given a training set
f
T S, a
validation set
c
T S and an objective function ϕ(e
1
, e
2
),
produce a recognition algorithm Al that satisfies the
following conditions:
1. Al should show limited number of type I and type
II errors on the training set
f
T S:
e
1
(Al,
f
T S) ≤ const
1
, e
2
(Al,
f
T S) ≤ const
2
(1)
Here e
i
(Al, T S) is the number of type i errors that
Al makes on the trajectories from T S.
A Genetic Algorithm for Training Recognizers of Latent Abnormal Behavior of Dynamic Systems
359
2. Al should minimize the objective function
ϕ(e
1
, e
2
) on the validation set
c
T S:
Al = arg min
Al
(ϕ(e
1
(Al,
c
T S), e
2
(Al,
c
T S))) (2)
The problem definition described here corre-
sponds to the classic definition of the problem of su-
pervised learning described in (Vorontsov, 2004) and
(Vapnik, 1998).
In this paper, our objective function is a linear
combination of the numbers of type I and type II er-
rors: ϕ(e
1
, e
2
) = a · e
1
+ b · e
2
, a, b > 0.
3 AXIOMATIC APPROACH TO
ABNORMAL BEHAVIOR
RECOGNITION
In this section we describe the parametric family of al-
gorithms for recognition of abnormal behavior of dy-
namic systems introduced in (Kovalenko et al., 2005).
3.1 Basic Notions
Let X = (x
1
, x
2
, ..., x
k
), be a one-dimensional trajec-
tory, x
t
∈ R.
An elementary condition ec = ec(t, X , p) is a
function defined on a point t and its neighborhood on
a trajectory X. It depends on a set of parameters p and
takes either true value or false value.
An example of an elementary condition is
ec(t, X , p) =
true, if ∀i ∈ [t − l, t + r]
a ≤ x
i
≤ b,
f alse, otherwise.
(3)
Here p = {a, b, l, r} is the set of parameters of
this elementary condition, a, b ∈ R, a < b, l, r ∈ N
+
.
This elementary condition is true whenever all
values of the trajectory X in a specific neighborhood
of point t lie between a and b.
Let X = (x
1
, x
2
, ..., x
k
) be a multidimensional tra-
jectory, x
i
∈ R
s
.
An axiom a = a(t, X) is a function defined as a
Boolean formula over a set of elementary conditions
defined on a point t and its neighborhood on a multi-
dimensional trajectory X:
a(t, X ) =
p
_
i=1
q
^
j=1
ec
i j
(t, X , p
i j
) (4)
We call a finite collection of axioms As =
{a
1
, a
2
, ..., a
m
} an axiom system if it meets the con-
dition:
∀X ∀x
t
∈ X ∃!a
i
∈ As : a(t,X) = true (5)
I. e. for any point t in any trajectory X there exists
one and only one axiom a
i
in axiom system As that is
true on point t.
Any finite collection of axioms as can be trans-
formed into an axiom system by:
1. Introducing an order in the collection by number-
ing axioms with consecutive integers:
as = {a
1
, a
2
, ..., a
M
}. (6)
We define that if an axiom with number i is true
on a point t of a phase trajectory, then no other
axiom of number j : j > i is true on t.
2. Adding to the set an axiom a
∞
that has the low-
est priority and is true at any point of any phase
trajectory:
As = {a
1
, a
2
, ..., a
M
, a
∞
}. (7)
A marking of a trajectory X = (x
1
, x
2
, ..., x
k
) by
an axiom system As = {a
1
, a
2
, ..., a
m
} is a finite se-
quence
J = ( j
1
, j
2
, . . . , j
k
) (8)
of numbers of axioms from as, such that a
j
t
is true on
the point t of trajectory X.
A marking of a reference abnormal behavior tra-
jectory of class l is called a model of abnormal be-
havior of class l. We denote the model of abnormal
behavior of class l as J
l
Anom
.
3.2 The Recognition Algorithm
In accordance with (Kostenko and Shcherbinin,
2013), we define our parametric family of recognition
algorithms S based on axiomatic approach as a family
of algorithms, each of which is defined by a tuple
Al = (As, {J
l
Anom
}
L
l=1
, A
search
), (9)
where As is an axiom system, {J
l
Anom
} is a set of ab-
normal behavior models – one for each class of ab-
normal behavior, A
search
is a fuzzy string search algo-
rithm.
Al recognizes abnormal behavior segments in tra-
jectory X by performing the following steps:
1. Perform marking of trajectory X by an axiom sys-
tem As. We denote the marking of trajectory X as
J.
2. Perform fuzzy search for abnormal behavior mod-
els {J
l
Anom
} in marking J using A
search
.
The use of fuzzy search algorithms for searching
for abnormal behavior models allows us to tackle time
distortions. Algorithms based on DTW (Keogh and
Pazzani, 2001) are used for marking search.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
360

To specify a recognition algorithm from paramet-
ric family S we need to construct an axiom system,
construct an abnormal behavior model for each class
of abnormal behavior and choose a fuzzy search al-
gorithm and its parameters. Local optimization algo-
rithms are used to adjust the parameters of marking
search algorithm. The greatest difficulty is posed by
construction of an axiom system and abnormal behav-
ior models.
3.3 Existing Algorithm for Constructing
Recognizers of Latent Abnormal
Behavior
Here we give a brief description of the algorithm from
(Kostenko and Shcherbinin, 2013) for construction
of an axiom system and abnormal behavior models
within the problem setting described in section 2.
The input of this algorithm includes a training
set
f
T S, a validation set
c
T S, an objective function
ϕ(e
1
, e
2
), the set of types of elementary conditions
to use.
We define intermediate objective function ψ(a) as
follows:
ψ(a) =
f req
f
T S
Anom
(a)
( f req
f
T S
Norm
(a) + δ)
, (10)
where f req
f
T S
Anom
(a) is the frequency of fulfillment of
an axiom a on the points of emergency trajectories of
f
T S, f req
f
T S
Norm
(a) is the frequency of fulfillment of an
axiom a on the points of normal trajectories of
f
T S, δ
is a predefined small positive value.
The algorithm consists of the following two
stages:
1. Selection of axioms. We form a set of axioms AX,
axioms from which are more frequently fulfilled
on emergency trajectories and less frequently ful-
filled on normal trajectories of the training set. To
do this, we perform the following steps:
(a) Selection of elementary conditions. This step
involves grid search for parameter values of
each type of elementary condition. We select
a predefined number of elementary conditions
which have the highest value of intermediate
objective function ψ.
(b) Construction of axioms from elementary con-
ditions. At this step the elementary conditions
selected at the previous step are iteratively com-
bined into axioms using OR and AND opera-
tions. Then a specified number of axioms with
the highest value of ψ is selected.
2. Construction of an axiom system and models of
abnormal behavior. Here we form a single-axiom
axiom system from each axiom in AX and itera-
tively add to each of the axiom systems an axiom
from AX while it decreases the objective function
ϕ on the validation set
c
T S. To calculate ϕ for an
axiom system As, we do the following:
(a) Construct the model of abnormal behavior for
each abnormal behavior class l as the longest
common subsequence (LCS) (Cormen et al.,
2001) of the markings by As of the emergency
trajectories of class l from the training set
f
T S.
(b) Use As and constructed models of abnormal be-
havior to recognize abnormal behavior in the
validation set
c
T S.
(c) Calculate the number of errors and the objective
function ϕ(e
1
, e
2
).
We stop when we can’t decrease ϕ anymore, or
when we exceed the predefined number of itera-
tions. The axiom system with the lowest ϕ is the
result of the algorithm.
The described algorithm has two distinctive fea-
tures. Firstly, the algorithm relies on the frequency
of fulfillment of axioms on training set trajectories to
select axioms for recognition of abnormal behavior.
This approach may not always produce axioms that
constitute good models of abnormal behavior. Sec-
ondly, the algorithm uses LCS to construct models
of abnormal behavior for a given axiom system. But
there may be abnormal behavior models other than the
LCS of the markings of emergency trajectories that
produce better recognition quality.
4 GENETIC TRAINING
ALGORITHM FOR LATENT
ABNORMAL BEHAVIOR
RECOGNIZERS
In this paper we propose a new algorithm for con-
struction of an axiom system and a set of abnormal
behavior models for recognition of latent abnormal
behavior. The new algorithm, similarly to the existing
one described in 3.3, has two stages: on the first stage
we construct a set of axioms AX , on the second stage
we select axioms from AX to form an axiom system
and models of abnormal behavior. On the first stage
we form AX in an unsupervised manner using clus-
tering of the trajectories of the training set. On the
second stage we employ a genetic algorithm to con-
struct the models of abnormal behavior and the axiom
system using axioms from AX.
A Genetic Algorithm for Training Recognizers of Latent Abnormal Behavior of Dynamic Systems
361

4.1 Construction of the Set of Axioms
For this stage we use the idea of time series clustering
from (Yairi et al., 2001). The purpose of this stage
is to construct axioms that meaningfully represent the
states of our dynamic system. This approach is dif-
ferent from the existing algorithm where we use fre-
quency of fulfillment of axioms to construct the set
AX.
We define a feature as a function that maps a
one-dimensional segment of a trajectory to a real
value. Examples of a feature are maximum, mini-
mum, mean, standard deviation.
To form the set of axioms AX, for each dimension
s of the trajectories we perform the following steps:
1. Randomly select a specified number of one-
dimensional segments with a specified length N
from the dimension s of trajectories of
f
T S.
2. Transform each selected segment into a vector of
feature values calculated for this segment. The set
of used features is a parameter of the algorithm.
3. Perform clustering of feature vectors using k-
means clustering (Hastie et al., 2001). After clus-
tering we get K centroid vectors.
4. Add to AX K axioms, where i-th axiom is of the
form:
a
i
(t, X ) =
true, if F(X
s
[t−d
N
2
e:t+b
N
2
c]
)
belongs to
i-th cluster,
f alse, otherwise.
(11)
Here F is a function that maps a one-dimensional
trajectory segment to a feature vector, X
s
[t
1
:t
2
]
is the
one-dimensional segment of dimension s of tra-
jectory X from point t
1
to point t
2
.
Thus each axiom corresponds to a cluster in the
feature space.
We define that a feature vector v belongs to the i-
th cluster if the centroid of i-th cluster is closer to v in
Euclidean metric than centroids of other clusters.
In this paper, the following features were used:
1. Minimum value.
2. Maximum value.
3. Standard deviation.
4. Linear regression coefficient (Hastie et al., 2001)
calculated using the following formula:
f (x
1
, x
2
, ..., x
N
) =
N
∑
i=1
(x
i
− x)(i −
1+N
2
)
N
∑
i=1
(i −
1+N
2
)
, (12)
where x
1
, x
2
, ..., x
N
are the values in the points of
the segment, x =
1
N
N
∑
i=1
x
i
4.2 Construction of an Axiom System
and the Models of Abnormal
Behavior
We construct the models of abnormal behavior and
the axiom system by means of a genetic algorithm.
The individual of the algorithm is a pair
(As, {J
l
Anom
}
L
l=1
), where As is an axiom system and
{J
l
Anom
}
L
l=1
is the set of abnormal behavior models
which use axioms from As. These can be viewed as
strings in the alphabet As.
The fitness function of the algorithm is the objec-
tive function ϕ(e
1
, e
2
) calculated on the validation set
c
T S. The goal of the algorithm is minimization of the
fitness function.
This stage consists of the following steps:
1. Generate initial population of size PSize.
2. Mutate each individual in the population, while
retaining the original individual, an add the mu-
tated individual to the population. Now the popu-
lation has size 2 · PSize.
3. Select 2·PSize pairs of individuals randomly from
the current population, perform crossover on them
(which yields 2 more individuals) and add the re-
sulting individuals to the population. Now the
population has size 4 · PSize.
4. Calculate the fitness function by running recogni-
tion on validation set
c
T S for each member of the
population.
5. Perform roulette wheel selection with elitism.
Form a new population of size PSize by select-
ing a specified fraction of the individuals of the
current population with the lowest fitness value
and selecting the rest of the new population using
roulette wheel selection.
6. Check the stopping criteria. If the speci-
fied number of iterations IMax is exceeded or
the best fitness function did not decrease for
IMaxNonDecrease iterations, stop. Otherwise,
return to step 2.
The result of the algorithm is the individual with the
lowest fitness value among the population after stop-
ping.
In this algorithm we evolve an axiom system and
the models of abnormal behavior. This is differ-
ent from the existing algorithm where axiom systems
are constructed separately and for each axiom system
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
362

only models of abnormal behavior based on the LCS
of the markings of emergency trajectories are consid-
ered.
In the rest of this section we describe the opera-
tions of the proposed genetic algorithm.
4.3 Generation of the Initial Population
Each individual (As, {J
l
Anom
}
L
l=1
) in the initial popu-
lation is generated in the following way:
1. As consists of a specified number of axioms ran-
domly chosen from AX.
2. Each model of abnormal behavior J
l
Anom
is formed
as the marking of a randomly chosen emergency
trajectory of class l from the training set
f
T S.
4.4 Mutation
To mutate an individual (As, {J
l
Anom
}
L
l=1
), we first
randomly select a class of abnormal behavior l, 1 ≤
l ≤ L. Mutation is performed on the model of abnor-
mal behavior of class l J
l
Anom
. We randomly select and
perform one of the following actions:
1. Insert a randomly chosen axiom a from As at a
random position into J
l
Anom
.
2. Insert a randomly chosen axiom a from AX \ As at
a random position into J
l
Anom
and add a to As with
a random priority.
3. Replace an element of J
l
Anom
at a randomly se-
lected position with a randomly chosen axiom a
from As.
4. Replace an element of J
l
Anom
at a randomly se-
lected position with a randomly chosen axiom a
from AX \ As. The axiom a is also added to As
with a random priority.
5. Remove an axiom at a random position of J
l
Anom
.
If the axiom does not occur in any of the models of
abnormal behavior anymore, remove it from As.
4.5 Crossover
To cross two individuals (As
1
, {J
l
1
}
L
l=1
) and
(As
2
, {J
l
2
}
L
l=1
), we first randomly select a class
of abnormal behavior l, 1 ≤ l ≤ L. The result
of the crossover operation is two new individu-
als: (As
0
1
, {J
1
1
, J
2
1
, ..., J
l−1
1
, J
0 l
1
, J
l+1
1
, ..., J
L
1
}) and
(As
0
2
, {J
1
2
, J
2
2
, ..., J
l−1
2
, J
0 l
2
J
l+1
2
, ..., J
L
2
}). The first
individual inherits all models of abnormal behavior
except the model of abnormal behavior of class
l from the first parent, similarly with the second
individual. For parents’ models of abnormal behavior
of class l we perform one-point crossover. Denoting
J
l
1
= ( j
l
1,1
, j
l
1,2
, ..., j
l
1, p
),
J
l
2
= ( j
l
2,1
, j
l
2,2
, ..., j
l
2,q
),
(13)
we select two random integers: r, 1 ≤ r ≤ p and s,
1 ≤ s ≤ q. New abnormal behavior models J
0 l
1
and J
0 l
2
are formed as follows:
J
0 l
1
= ( j
l
1,1
, j
l
1,2
, ..., j
l
1,r
, j
l
2,s+1
, ..., j
l
2,q
),
J
0 l
2
= ( j
l
2,1
, j
l
2,2
, ..., j
l
2,s
, j
l
1,r+1
, ..., j
l
1, p
).
(14)
The axiom system As
0
i
, i ∈ {1, 2} of the offspring
individual is inherited from the ith parent and then ad-
justed so that if an axiom is not present in any models
of abnormal behavior anymore, it is removed from the
axiom system, an if a new axiom that is not present in
As
i
is added to J
0 l
i
, it is added to the axiom system
with a random priority.
5 EXPERIMENTAL EVALUATION
During experimental evaluation we compared the ex-
isting algorithm described in section 3.3 (denoted as
A
orig
) with the proposed algorithm described in sec-
tion 4 (denoted as A
clust genetic
). We also experimented
with the following two algorithms:
• An algorithm where the first stage is from the ex-
isting algorithm (i. e. we construct the set of ax-
ioms AX using the frequency of fulfillment of ax-
ioms on the trajectories of the training set), and
the second stage is from the proposed algorithm
(i. e. the genetic algorithm described in section
4.2). We denote this algorithm as A
genetic
.
• An algorithm where the first stage is from the pro-
posed algorithm (i. e. we construct the set of
axioms AX using clustering of the trajectories of
the training set, as described in section 4.1) and
the second stage is from the existing algorithm
(i. e. the axiom system and the models of ab-
normal behavior are constructed using simple di-
rected search). We denote this algorithm as A
clust
.
The objective function used during the experi-
ments was ϕ(e
1
, e
2
) = e
1
+ 20 · e
2
. The coefficient
for type II errors is greater because type II errors are
usually more costly than type I errors.
The experiments were conducted using synthetic
data.
5.1 Synthetic Data
Consider a finite alphabet Σ where each symbol x ∈ Σ
corresponds to a segment of a one-dimensional trajec-
tory. Then a string s in this alphabet corresponds to a
A Genetic Algorithm for Training Recognizers of Latent Abnormal Behavior of Dynamic Systems
363
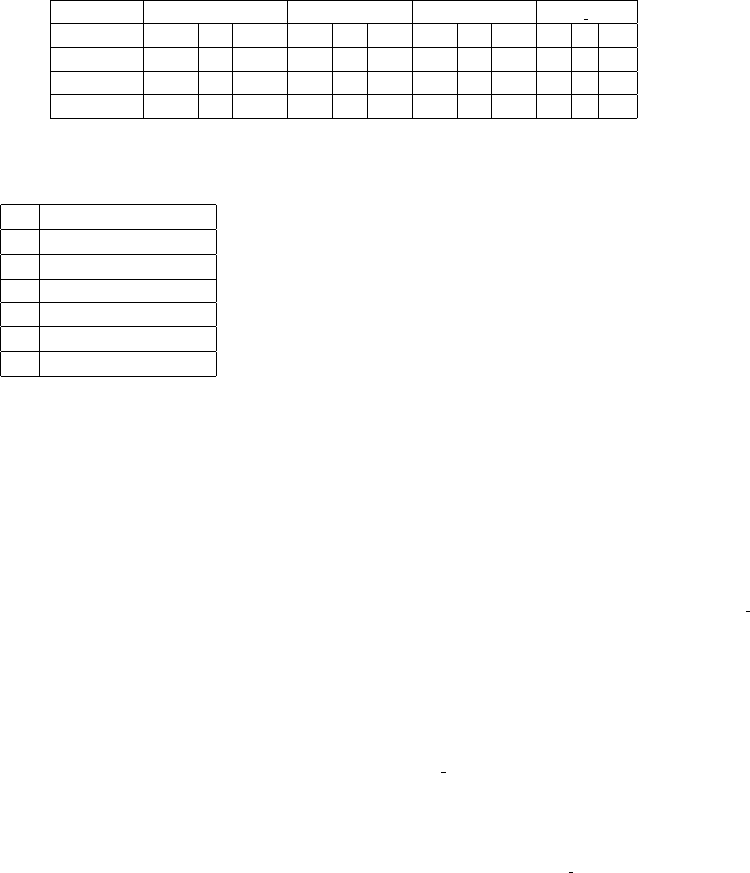
Table 2: Summary of the results. For each of the considered algorithms the table shows maximum, minimum and average
numbers of type I and type II errors and the value of the objective function ϕ for the recognizer trained with the corresponding
algorithm.
A
orig
A
clust
A
genetic
A
clust genetic
e
1
e
2
ϕ e
1
e
2
ϕ e
1
e
2
ϕ e
1
e
2
ϕ
Maximum 1872 8 1872 70 6 174 82 3 104 77 1 97
Minimum 2 0 10 1 0 1 2 0 2 0 0 0
Average 111.7 1.1 133.8 10.3 0.1 11.8 15.4 0.1 17.1 5.4 0 5.7
Table 1: The functions used to generate segments of exper-
imental data alphabet.
A y = x
3
B y = −x
3
C y = −(x − 5)
2
+ 25
D y = −x
E y = x
F y = (x − 5)
2
− 25
G y = x
2
trajectory X which is a result of concatenation of the
segments corresponding to the symbols of the string.
We call such a string s a signature of the trajectory X .
For generation of the data for the experiments, we
consider an alphabet of segments which correspond
to values of functions shown in table 1 in the points
x = 0, 1, ..., 9. Each segment therefore has length 10.
Each dataset generated for the experiments had 1
dimension, 1 class of abnormal behavior, 20 emer-
gency trajectories and 20 normal trajectories. Emer-
gency trajectories were generated in the following
way:
1. A signature s for the abnormal behavior segment
was generated. The signature contained from 3 to
6 symbols.
2. Signatures containing 10 symbols were generated
randomly for each emergency trajectory, then the
signature of abnormal behavior segment was in-
serted at a random position in each signature of
emergency trajectory. We also ensured that each
signature of emergency trajectory had only one
substring corresponding to the signature of abnor-
mal behavior segment.
3. Signatures containing 10 symbols were generated
randomly for each normal trajectory. We took
care to generate normal trajectory signatures that
don’t contain abnormal behavior segment signa-
ture as a substring.
4. Each signature of emergency and normal trajec-
tory was converted to the trajectory itself, during
this process distortions were added:
• Non-linear time distortion was added by ran-
domly and independently shrinking each seg-
ment up to 50% or growing it up to 200% of
the original size.
• Amplitude distortion was added by applying
Gaussian noise with σ = 3 to the resulting tra-
jectory.
Note that because of the time distortion the length
of each resulting trajectory could vary from 50 to 200
points.
5.2 Results
A total number of 132 experiments were conducted.
The results of the experiments are summarized in ta-
ble 2.
Using the binomial test (Conover, 1971), we were
able to prove the following hypotheses with signifi-
cance level α = 0.05:
• Each of the algorithms A
clust
, A
genetic
, A
clust genetic
with probability at least 0.9 trains a recognizer
that delivers a lower value of the objective func-
tion ϕ on validation set than the best recog-
nizer constructed by A
orig
. We considered the
alternative hypothesis that the probability of the
event that each of the algorithms A
clust
, A
genetic
,
A
clust genetic
trains a recognizer whose objective
function value is less than the objective function
value of the recognizer trained by A
orig
is less than
0.9. The p-value for the binomial test was 0.007.
• The algorithm A
clust genetic
with probability 0.8
trains a recognizer that has 50% less type I er-
rors and no more type II errors than the recognizer
trained by A
orig
. The p-value for the binomial test
was 0.022.
• The algorithm A
clust
with probability 0.8 trains a
recognizer that has 10% less type I errors and no
more type II errors than the recognizer trained by
A
orig
. The p-value for the binomial test was also
0.022.
Running times for each algorithm on a machine
with processor Intel(R) Core(TM) i5-2520M CPU
2.50 GHz, 64 L1-cache and 4GB RAM is shown in
Table 3.
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
364
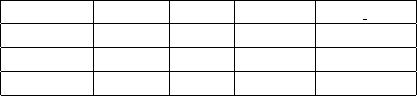
Table 3: Average, maximum and minimum running times
for each algorithm.
A
orig
A
clust
A
genetic
A
clust genetic
Maximum 195 min 61 sec 80 min 26 min
Minimum 1.6 min 2 sec 6 min 2 min
Average 7.8 min 9.8 sec 19.7 min 8.7 min
6 CONCLUSION
This paper considers the problem of automatic con-
struction of algorithms that recognize segments of ab-
normal behavior in multidimensional phase trajecto-
ries of dynamic systems. The recognizers are con-
structed using a training set of example trajectories of
normal and abnormal behavior of the system. The no-
table feature of the problem setting considered by this
paper is that the exact position of the segments corre-
sponding to abnormal behavior in the trajectories of
the training set is unknown.
This paper proposes a two-step algorithm for
training recognizers of abnormal behavior of dynamic
systems. On the first step, axioms corresponding to
typical patterns of the trajectories are constructed by
clustering the trajectories of the training set. On the
second step, genetic algorithm is used to construct the
models of abnormal behavior of the dynamic system
from the axioms obtained on the first step.
The proposed algorithm and its variations were
empirically evaluated on synthetic data. The results of
conducted experiments show that the proposed algo-
rithm is able to improve recognition quality of trained
recognizers compared to the existing training algo-
rithm. On synthetic data, we were able to prove with
significance level 0.05 a statistical hypothesis that the
recognizer trained by the proposed algorithm with
probability 0.8 makes 50% less type I errors and no
more type II errors than the one trained by the exist-
ing algorithm.
For the variation of the proposed algorithm based
on clustering and directed search, we were able
to prove a statistical hypothesis that the recognizer
trained by this algorithm with probability 0.8 makes
10% less type I errors and no more type II errors than
the one trained by the existing algorithm. The advan-
tage of this variation of the algorithm is that it runs
considerably faster than the existing algorithm or the
algorithm based on clustering and genetics (for syn-
thetic data, average time was 9.8 seconds vs 7.8 min-
utes for the existing algorithm and 8.7 minutes for the
algorithm based on clustering and genetics).
REFERENCES
Conover, W. J. (1971). Practical nonparametric statistics.
John Wiley & Sons, New York.
Cormen, T. H., Stein, C., Rivest, R. L., and Leiserson, C. E.
(2001). Introduction to Algorithms. McGraw-Hill
Higher Education, 2nd edition.
Cover, T. and Hart, P. (1967). Nearest neighbor pattern clas-
sification. Information Theory, IEEE Transactions on,
13(1):21–27.
Hassani, H. (2007). Singular spectrum analysis: Method-
ology and comparison. Journal of Data Science,
5(2):239–257.
Hastie, T., Tibshirani, R., and Friedman, J. (2001). The
Elements of Statistical Learning. Springer Series in
Statistics. Springer New York Inc., New York, NY,
USA.
Haykin, S. (1998). Neural Networks: A Comprehensive
Foundation. Prentice Hall PTR, Upper Saddle River,
NJ, USA, 2nd edition.
Keogh, E. J. and Pazzani, M. J. (2001). Derivative dynamic
time warping. In First SIAM International Conference
on Data Mining (SDM2001).
Kostenko, V. A. and Shcherbinin, V. V. (2013). Training
methods and algorithms for recognition of nonlinearly
distorted phase trajectories of dynamic systems. Opti-
cal Memory and Neural Networks, 22:8–20.
Kovalenko, D. S., Kostenko, V. A., and Vasin, E. A. (2005).
Investigation of applicability of algebraic approach to
analysis of time series. In Proceedings of II Interna-
tional Conference on Methods and Tools for Informa-
tion Processing, pages 553–559. (in Russian).
Kovalenko, D. S., Kostenko, V. A., and Vasin, E. A. (2010).
A genetic algorithm for construction of recognizers
of anomalies in behaviour of dynamical systems. In
Proceedings of 5th IEEE Int. Conf. on Bio Inspired
Computing: Theories and Applications, pages 258–
263. IEEEPress.
Rudakov, K. V. and Chekhovich, Y. V. (2003). Algebraic
approach to the problem of synthesis of trainable al-
gorithms for trend revealing. Doklady Mathematics,
67(1):127–130.
Shcherbinin, V. V. and Kostenko, V. A. (2013). A modifica-
tion of training and recognition algorithms for recog-
nition of abnormal behavior of dynamic systems. In
Proceedings of the 5th International Joint Conference
on Computational Intelligence, pages 103–110.
Vapnik, V. (1998). Statistical Learning Theory. Wiley-
Interscience.
Vorontsov, K. V. (2004). Combinatorial substantiation of
learning algorithms. Journal of Comp. Maths Math.
Phys, 44(11):1997–2009.
Yairi, T., Kato, Y., and Hori, K. (2001). Fault detection by
mining association rules from house-keeping data. In
Proc. of International Symposium on Artificial Intelli-
gence, Robotics and Automation in Space.
A Genetic Algorithm for Training Recognizers of Latent Abnormal Behavior of Dynamic Systems
365
