A Fuzzy Poisson Naive Bayes Classifier for Epidemiological Purposes
Ronei M. Moraes
1
and Liliane S. Machado
2
1
Department of Statistics, Federal University of Paraiba, Paraiba, Brazil
2
Department of Informatics, Federal University of Paraiba, Paraiba, Brazil
Keywords:
Classification, Fuzzy Poisson Naive Bayes, Epidemiology.
Abstract:
Statistical methods have been used to classify data in different areas. In epidemiological studies, some mea-
sures follow specific statistical distribution and compatible classifiers can be designed for those cases. Clas-
sifiers based on measures that follow Poisson distributions can be found in the scientific literature. Due to
uncertainty on epidemiological measures, a fuzzy approach may be interesting and the present work proposes
a new classifier named Fuzzy Poisson Naive Bayes (FPNB). The theoretical development is presented as well
as results of its application on simulated multidimensional data. A brief comparison with a classical Poisson
Naive Bayes classifier and with a Naive Bayes classifier is performed too.
1 INTRODUCTION
Several kind of classifiers can be found in the sci-
entific literature and applied in different areas, as
pattern recognition (Kim et al., 2003), image pro-
cessing (Richards, 2013) and psychomotor skills as-
sessment of training based on virtual reality (Moraes
and Machado, 2014). There are classifiers designed
for Multinomial (Duda et al., 2000), Beta (Moraes
et al., 2012) (Moraes et al., 2014), Binomial (Bielza
and Larranaga, 2014), Gaussian (Johnson and Wich-
ern, 2007), Fuzzy Gaussian (Moraes and Machado,
2012) and mixture of distributions (Melo et al., 2003)
(Ogura et al., 2014). Some of them can be applied
without taking into account the statistical distribution
followed by the data, as neural networks (Bishop,
2007), genetic algorithms and decision trees (Cong-
don, 2000), K-NN (Vadrevu and Murty, 2010) and
Fuzzy K-NN (Keller et al., 1985). For this last case, it
can be observed a generalized use of classifiers, even-
tually with acceptable results. However, it is also pos-
sible to find cases of use of non suitable classifiers for
that distribution of statistical data, resulting in per-
formances lower than expected or even poor perfor-
mances.
Some measures follow specific statistical distri-
bution and classifiers compatible with each case can
be designed. For example, the number of registered
cases of a particular disease in a period of time fol-
lows Poisson distribution (Feller, 1971). This dis-
tribution can also be used for other epidemiological
measures and it has been applied in other areas. For
instance, when the probability of a disease is small
and the total number of the population is large, Pois-
son distribution provides a good approximation for
Binomial distribution, with an important advantage:
it is easier to be computed than the last one. Classi-
fiers based on Poisson distribution are interesting for
applications in other areas too. In fact, Poisson Naive
Bayes Classifier (PNB) has been applied to text clas-
sification (Altheneyan and Menai, 2014) (Kim et al.,
2003) and neurosciences (Ma et al., 2006), among
others.
However, the uncertainty on epidemiological
measures, which may be underestimated due to fail-
ure in data collection, or overestimated due to sup-
posed unconfirmed diagnoses (Rothman et al., 2012),
suggests that a fuzzy approach may be more appropri-
ate. So, a new approach based on Poisson distribution
and fuzzy data can be interesting to generate classifi-
cations from epidemiological measures.
This paper is organized as following: the Section
2 presents some theoretical aspects of probability of
fuzzy events and introduces a new classifier based on
Poisson distribution and fuzzy data. The Section 3
brings results from the application of the new method
in simulated Poisson distributed data. Comparisons
with two classifiers are performed in the Section 4:
classical Poisson Naive Bayes and Naive Bayes. Fi-
nally, the conclusions are provided in the last section.
Moraes, R. and Machado, L..
A Fuzzy Poisson Naive Bayes Classifier for Epidemiological Purposes.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 2: FCTA, pages 193-198
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
193

2 METHODOLOGY
For better understanding of the classifier proposed,
some theoretical considerations need to be provided.
Firstly, it is defined the concept of Naive Bayes classi-
fier, followed by the concept of Poisson Naive Bayes
classifier and by the new Fuzzy Poisson Naive Bayes
classifier proposition. After those ones, details about
the epidemiological simulation are provided. Finally,
is introduced the Kappa Coefficient, which is used to
perform statistical analysis of results.
2.1 Naive Bayes Classifier
Formally, let be the classes of performance in space
of decision Ω = {1, ...,M} where M is the total num-
ber of classes. Let be a vector of training data X, ac-
cording to sample data D, where X is a vector with n
distinct features, i.e. X = {X
1
,X
2
,, X
n
} and w
i
, i ∈ Ω
is the class in space of decision for the vector X. So,
the probability of the class w
i
, given the vector X, can
be estimated using the Bayes Theorem:
P(w
i
|X) =
P(X|w
i
)P(w
i
)
P(X)
=
=
P(X
1
,X
2
,. .., X
n
|w
i
)P(w
i
)
P(X)
(1)
The computation of equation (1) has complexity
directly proportional to the increase of the number k
of variables. An alternative is assuming the naive hy-
pothesis (Duda et al., 2000), in which each feature X
k
is conditionally independent of every other feature X
l
,
for all k 6= l ≤ n. This hypothesis, though sometimes
it is not exactly realistic, enables an easier calculation
of equation (1). As advantage of that assumption is
the strength of the Naive Bayes (NB) classifier and
the fact that it can classify data for which it was not
trained for (Ramoni and Sebastiani, 2001). So, unless
a scale factor S, which depends on X
1
,X
2
,. .., X
n
, the
equation (1) can be expressed by:
P(w
i
|X
1
,X
2
,. .., X
n
) =
1
S
P(w
i
)
n
∏
k=1
P(X
k
|w
i
) (2)
The classification rule for NB is:
X ∈ w
i
if P(w
i
|X
1
,X
2
,. .., X
n
) > P(w
j
|X
1
,X
2
,. .., X
n
)
(3)
for all i 6= j and the probability P is given by (2).
2.2 Poisson Naive Bayes Classifier
A possible approach for Naive Bayes classifier is to
assume Poisson distribution for each X
i
, where:
P(X
k
= v|w
i
) =
λ
v
ki
e
−λ
ki
v!
(4)
where v = 0,1,2, ..., v! is the factorial of v, and com-
pute its parameter from D, i.e., the mean λ
ki
(for vari-
able X
k
and the class i) (Feller, 1971). From equa-
tion (2) it is possible to use the logarithm function to
simplify the exponential function in the Poisson dis-
tribution formula (equation 4) and, consequently, to
reduce computational complexity by replacing multi-
plications by additions. So, the Poisson Naive Bayes
(PNB) classifier is given by:
g (w
i
,X
1
,X
2
,. .., X
n
) = log[P(w
i
|X
1
,X
2
,. .., X
n
)]
= log(1/S) + logP(w
i
) +
n
∑
k=1
log[P(X
k
|w
i
)] (5)
where g is the classification function and P(X
k
|w
i
) is
given by (4). The log[P(X
k
|w
i
)] in the equation (5)
can be rewritten as:
log [P(X
k
= v|w
i
)] = log
"
λ
v
ki
e
−λ
ki
v!
#
=
= v × log(λ
ki
) − λ
ki
− log(v!). (6)
The classification rule for PNB is:
X ∈ w
i
if g(w
i
,X
1
,X
2
,. .., X
n
) > g(w
j
,X
1
,X
2
,. .., X
n
)
(7)
for all i 6= j and the function g is given by (5).
2.3 Fuzzy Poisson Naive Bayes
Classifier
Zadeh introduced a probability measure for fuzzy
events (Zadeh, 1968). Let B be a σ-field of Borel sub-
sets in R
n
and P be a probability measure over Ω. Let
A be a fuzzy event in B. Thus, the probability of A
can be expressed as a Lebesgue-Sieltjes integral:
P(A) =
Z
A⊆R
n
dP =
Z
A⊆R
n
µ
A
(x) dP = E(µ
a
) (8)
So, the probability of a fuzzy event A is the
mathematical expectation of its membership function,
which can be written as:
P(A) =
Z
A⊆R
n
µ
A
(x) P(x) dx (9)
At this point, it is assumed that X
1
,X
2
,. .., X
n
are
also fuzzy variables (Klir and Yuan, 1995), and for
each one a membership function µ
w
i
(X
k
) is available
for all k 6 n. Then, based on probability of a fuzzy
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
194

event (Zadeh, 1968) given by the equation (9), the
Fuzzy Poisson Naive Bayes (FPNB) classifier is done
by:
g
f
(w
i
,X
1
,X
2
,. .., X
n
) = log[P(w
i
|X
1
,X
2
,. .., X
n
)] =
= log(1/S
f
) + logP(w
i
) +
+
n
∑
k=1
log[µ
wi
(X
k
)] + log[P(X
k
|w
i
)] (10)
where g
f
is the new classification function, S
f
is a new
scale factor and log[P(X
k
|w
i
)] is given by (6).
The necessary parameters for computing of
P(X
k
|w
i
) and µ
wi
(X
k
) should be learned from sample
data D. The better estimation for class of the vector X
can be obtained from the highest values of the classi-
fication function g
f
. However, as S
f
is a scale factor,
it is not necessary to computed it in this maximization
process. Then, from the equations (10) and (6):
g
f
(w
i
,X
1
,X
2
,. .., X
n
) = logP(w
i
) +
+
n
∑
k=1
log[µ
wi
(X
k
)] + v × log(λ
ki
) − λ
ki
− log(v!)
(11)
Finally, the classification rule for FPNB is:
X ∈ w
i
if g
f
(w
i
,X
1
,X
2
,. .., X
n
) >
> g
f
(w
j
,X
1
,X
2
,. .., X
n
) (12)
for all i 6= j and the functions g
f
are given by (11).
2.3.1 Parameters Estimation
In this paper, two estimators for λ using sample data
D are presented. The first one is the maximum likeli-
hood estimator, which is given by (Feller, 1971):
ˆ
λ
ki
=
1
dim(D)
×
dim(D)
∑
k=1
(X
k
,w
i
) (13)
where dim(D) is the length of sample data D for
which the class is w
i
and
∑
dim(D)
k=1
(X
k
,w
i
) is the count-
ing of events in D, in which the value of X
k
is associ-
ated to the class w
i
.
The second estimator is given by (Ogura et al.,
2014):
ˆ
λ
ki
=
c
1
+
∑
dim(D)
k=1
(X
k
,w
i
)
c
2
+ dim(D)
(14)
where c
1
and c
2
are smoothing parameters (constants)
used to prevent estimations with value zero for
ˆ
λ
ki
.
Thus, using the estimators provided by equation
(13) or (14) is possible to compute g
f
from the equa-
tion (11) for each class w
i
. In this paper, the estimator
provided by equation (14) is used and the parameters
c
1
= 0.1 and c
2
= 1 are set.
The membership functions µ
wi
(X
k
) should be
learned from sample data D. A possible ap-
proach is obtain them from normalized relative fre-
quency histograms of X
k
variables (Dubois and Prade,
1983)(Kaufmann et al., 2015).
2.4 Simulations
In order to assess the new classifier, a Monte Carlo
simulation was used for the counting of new regis-
tered cases of three diseases. In practical situation,
they could be three communicable diseases. The first
one is a vector-born disease: dengue fever, whose
vector in Brazil is the Aedes aegypti mosquito. The
second disease is HIV-AIDS and the third one is tu-
berculosis, which are spread person-to-person.
According to that situation, the goal is to predict
the class of epidemiological priority of municipali-
ties to support actions against those diseases. Thus,
databases with 200 observations (municipalities) for
each disease were generated to contain the three dif-
ferent diseases with three Poisson distributions using
different parameters. Each line of database simulates
the number of morbidities registered for each disease
for the municipalities. Three levels of priority were
defined for all cases, according to the statistical ter-
ciles calculated in the training database for each dis-
ease. After that, a logical combination of those ter-
ciles defines the priority level of a municipality in:
low level, medium level and high level.
In total, 40 double databases were created, where
the first one is for training and the second one is for
testing. The same Poisson parameters were used to
create both of them. However, those parameters were
changed for each double in order to know the variabil-
ity of the classification results.
2.5 Coefficient of Agreement
Assessment
A statistical comparison between two different classi-
fiers using several statistical coefficients (Duda et al.,
2000) was performed. In the literature of Pattern
Recognition, a robust pondered measure which takes
into account agreements and disagreements between
two sources of information (Viera and Garrett, 2005)
is the Kappa Coefficient, proposed by Cohen (Cohen,
1960) and given by:
A Fuzzy Poisson Naive Bayes Classifier for Epidemiological Purposes
195
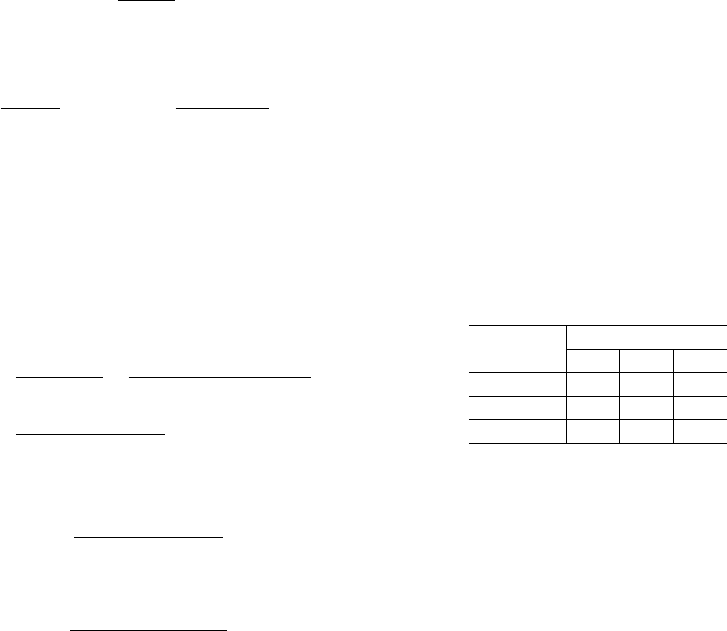
K =
P
0
− P
c
1 − P
c
, (15)
where:
P
0
=
∑
M
i=1
n
ii
N
and P
c
=
∑
M
i=1
n
i+
n
+i
N
2
(16)
with n
ii
as elements of the main diagonal of classifi-
cation matrix; n
i+
as the total of line i in the classifi-
cation matrix, n
+i
as the total of column in the same
matrix, M as the number of possible classes and N as
the total number of possible decision presented in the
matrix.
The variance of Kappa Coefficient, denoted by
σ
2
K
is given by:
σ
2
K
=
P
0
(1 − P
0
)
N(1 − P
c
)
2
+
2(1 − P
0
) + 2P
0
P
c
− θ
1
N(1 − P
c
)
3
+
+
(1 − P
0
)
2
θ
2
− 4P
c
2
N(1 − P
c
)
4
, (17)
where θ
1
is given by:
θ
1
=
∑
M
i=1
n
ii
(n
i+
+ n
+i
)
N
2
, (18)
and θ
2
is given by:
θ
2
=
∑
M
i=1
n
ii
(n
i+
+ n
+i
)
2
N
3
, (19)
respectively.
3 RESULTS
Using the 40 databases created from the simulations
described in the Section 2.4, the FPNB classifier was
used to assing one of three levels of epidemiological
priority for each municipality simulated in databases.
Firstly, a file with training samples was used to esti-
mate the parameters of FPNB classifier. After that,
the second file with testing samples was used to eval-
uate the performance of FPNB classifier.
In order to provide closer to reality simulations,
the λ parameters used were obtained from Epidemi-
ological Bulletins from Brazilian Ministry of Health
and are reproduced below:
• Dengue fever: 282.2 cases by 100,000 inhabitants
(Surveillance, 2014);
• HIV-AIDS: 20.2 cases by 100,000 inhabitants
(Surveillance, 2013);
• Tuberculosis: 33.5 cases by 100,000 inhabitants
(Surveillance, 2015).
The best result obtained, according to Kappa Co-
efficient, can be observed in the classification matrix
presented in Table 1. In that table, the main diagonal
of the matrix brings the correct classification. Outside
of the main diagonal are presented all errors of classi-
fication. The Kappa Coefficient was used to perform
the comparison of the classification agreement. From
the classification matrix obtained, the Kappa coeffi-
cient for all samples was K = 62.0% with variance
7.091×10
−4
. The FPNB made mistakes in 152 cases.
That performance is very acceptable and it shows the
good adaptation of FPNB in the solution of this kind
of problem.
Table 1: Classification matrix for the FPNB classifier.
Database
FPNB
1 2 3
1 148 50 2
2 36 128 36
3 1 27 172
Another important result is the computational per-
formance of the FPNB classifier: with a Core 2 Duo
PC compatible with 2GB of RAM, the average time
of CPU consumed by the assessment was 0.3590 sec-
onds. Then, it is possible to affirm that the FPNB has
low computational complexity.
4 COMPARISON WITH OTHER
CLASSIFIERS
A comparison was performed between the FPNB with
other two classifiers described in this paper: the PNB
and the NB classifiers. All of them were configured
using the same methodology mentioned before. Thus,
the same samples of training were used to obtain the
parameters for both classifiers, and the same sam-
ples of testing were used for a controlled and impar-
tial comparison among the classifiers. The CPU time
used by both classifiers in the classifications tasks
were measured.
The classification matrix obtained for the PNB
classifier is presented in the Table 2. The Kappa coef-
ficient was K = 58.25% with variance 7.4987 × 10
−4
,
and there were 167 misclassifications. The classifica-
tion task demanded 0.1400 seconds of CPU.
The NB classifier provided the classification ma-
trix presented in the Table 3. For this classifier, the
Kappa coefficient was K = 41.5000% with variance
9.0710 × 10
−4
, demanding 0.5140 seconds of CPU.
In this case, there were 234 misclassifications.
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
196
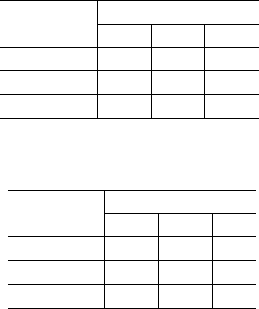
Table 2: Classification matrix for the PNB classifier.
Database
PNB
1 2 3
1 156 43 1
2 50 113 37
3 2 34 164
Table 3: Classification matrix for the NB classifier.
Database
NB
1 2 3
1 173 27 0
2 87 106 7
3 25 88 87
It is possible to see by Tables 1, 2, 3 and by Kappa
coefficients that the performance of the FPNB clas-
sifier is better than both other classifiers. In statis-
tical terms, the difference of performance between
those assessment methods can be considered signif-
icant. Observing the computational performance, the
FPNB was faster than the one based on NB, but PNB
is the fastest.
5 CONCLUSIONS
In this paper was presented a new classifier based on
Fuzzy Poisson Naive Bayes. Classifiers based on this
approach can be applied to epidemiological studies as
well as to other areas of human knowledge, as text
classification and neurosciences.
The Fuzzy Poisson Naive Bayes performance was
compared with other classifiers performance based on
Poisson Naive Bayes and Naive Bayes. The results
obtained showed that the first one presents signifi-
cant better classifications than the others. The Pois-
son Naive Bayes classifier provided competitive re-
sults and the Naive Bayes classifier provided the worst
results.
In terms of CPU time, the Fuzzy Poisson Naive
Bayes was faster than the Naive Bayes, but Poisson
Naive Bayes is the fastest. The new classifier pointed
out a competitive approach to solve problems in Epi-
demiology.
ACKNOWLEDGEMENTS
This project is partially supported by grants
310561/2012-4 and 310470/2012-9 of the National
Council for Scientific and Technological Develop-
ment (CNPq) and is related to the National Insti-
tute of Science and Technology “Medicine Assisted
by Scientific Computing”(181813/2010-6) also sup-
ported by CNPq.
REFERENCES
Altheneyan, A. S. and Menai, M. E. B. (2014). Naive bayes
classifiers for authorship attribution of arabic texts.
Journal of King Saud University Computer and In-
formation Sciences, 26(4):473–484.
Bielza, C. and Larranaga, P. (2014). Discrete bayesian net-
work classifiers: A survey. ACM Computing Surveys,
47(1):Article 5.
Bishop, C. (2007). Pattern Recognition and Machine
Learning. Springer, Berlin, 1st edition.
Cohen, J. (1960). A coefficient of agreement for nominal
scales. Educat. Psyc. Measurement, 20(1):37–46.
Congdon, C. B. (2000). Classification of epidemiological
data: a comparison of genetic algorithm and decision
tree approaches. In Proceedings of the 2000 Congress
on Evolutionary Computation, pages 442–449.
Dubois, D. and Prade, H. (1983). Unfair coins and neces-
sity measures: Towards a possibilistic interpretation
of histograms. Fuzzy Sets and Systems, 10(1-3):1520.
Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pat-
tern Classification. Wiley Interscience, New York,
2nd edition.
Feller, W. (1971). An Introduction to Probability Theory
and its Applications. Wiley, 2nd edition.
Johnson, R. A. and Wichern, D. W. (2007). Applied Multi-
variate Statistical Analysis. Pearson, 6th edition.
Kaufmann, M., Meier, A., and Stoffel, K. (2015). Ifc-
filter: Membership function generation for inductive
fuzzy classification. Expert Systems with Applica-
tions, 42:83698379.
Keller, J. M., Gray, M. R., and Givens, J. A. (1985). A
fuzzy k-nearest neighbor algoritm. IEEE Trans. Syst.
Man and Cybernetics, 15(4):580–585.
Kim, S.-B., Seo, H.-C., and Rim, H.-C. (2003). Poisson
naive bayes for text classification with feature weight-
ing. In Proceedings of the Sixth International Work-
shop on Information Retrieval with Asian Languages,
pages 33–40.
Klir, G. J. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic:
Theory and Applications. Prentice Hall, 1st edition.
Ma, W. J., Beck, J. M., Latham, P. E., and Pouget, A.
(2006). Bayesian inference with probabilistic popu-
lation codes. Nature Neuroscience, 9(11):1432–1438.
Melo, A. C. O., Moraes, R. M., and Machado, L. S. (2003).
Gaussian mixture models for supervised classifica-
tion of remote sensing muliespectral images. Lecture
Notes in Computer Science, 2905:440–447.
Moraes, R. M. and Machado, L. S. (2012). Online assess-
ment in medical simulators based on virtual reality us-
ing fuzzy gaussian naive bayes. Journal of Multiple-
Valued Logic and Soft Computing, 18(5-6):479–492.
A Fuzzy Poisson Naive Bayes Classifier for Epidemiological Purposes
197
Moraes, R. M. and Machado, L. S. (2014). Psychomo-
tor skills assessment in medical training based on vir-
tual reality using a weighted possibilistic approach.
Knowledge Based Systems, 70:97–102.
Moraes, R. M., Rocha, A. V., and Machado, L. S. (2012).
Intelligent assessment based on beta regression for re-
alistic training on medical simulators. Knowledge-
Based Systems, 32:3–8.
Moraes, R. M., Simas, A. B., Rocha, A. V., and Machado,
L. S. (2014). New parameters estimators using em-
like algorithm for naive bayes classifier based on
beta distributions. In 11th International FLINS Con-
ference on Decision Making and Soft Computing
(FLINS2014), pages 155–160, Brazil. World Scien-
tific.
Ogura, H., Amano, H., and Kondo, M. (2014). Classi-
fying documents with poisson mixtures. Transac-
tions on Machine Learning and Artificial Intelligence,
2(4):48–76.
Ramoni, M. and Sebastiani, P. (2001). Robust bayes classi-
fiers. Artificial Intelligence, 125(1-2):209–226.
Richards, J. A. (2013). Remote Sensing Digital Image Anal-
ysis: An Introduction. Springer, 5th edition.
Rothman, K. J., Lash, T. L., and Greenland, S. (2012). Mod-
ern Epidemiology. Wolters Kluwer, 3rd edition.
Surveillance, H. (2013). Aids e dst. Epidemiological Bul-
letin: HIV-AIDS - Secretariat of Health Surveillance -
Brazilian Ministry of Health, 2(1):1–16.
Surveillance, H. (2014). Monitoramento dos casos de
dengue e febre de chikungunya ate a semana epidemi-
ologica 47 de 2014. Epidemiological Bulletin - Sec-
retariat of Health Surveillance - Brazilian Ministry of
Health, 45(31):1–7.
Surveillance, H. (2015). Detectar, tratar e curar: desafios
e estratgias brasileiras frente tuberculose. Epidemio-
logical Bulletin - Secretariat of Health Surveillance -
Brazilian Ministry of Health, 46(9):1–19.
Vadrevu, S. H. R. and Murty, S. U. (2010). A novel tool for
classification of epidemiological data of vector-borne
diseases. J. Glob Infect Dis., 2(1):35–38.
Viera, A. J. and Garrett, J. M. (2005). Understanding in-
terobserver agreement: The kappa statistic. Family
Medicine, 37(5):360–363.
Zadeh, L. A. (1968). Probability measures of fuzzy events.
J. Math. Anal. Applic., 10:421–427.
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
198
