Fast Automated Interictal Spike Detection in iEEG/ECoG Recordings
Using Optimized Memory Access
Filip Kesner
1,2
, Jan Cimbalnik
2
, Irena Dolezalova
3
, Milan Brazdil
3
and Lukas Sekanina
1
1
Faculty of Information Technology, Brno University of Technology,
Brno, Czech Republic
2
International Clinical Research Center, Center of Biomedical Engineering,
St. Annes University Hospital, Brno, Czech Republic
3
1st Department of Neurology, St. Annes University Hospital and Medical Faculty,
Masaryk University, Brno, Czech Republic
1 MOTIVATION
Interictal spikes have been established as an impor-
tant biomarker in surface EEG and intracranial iEEG
recordings for some time (Staley et al., 2011). Spikes
are used for clinical practice and research of epilepsy,
ADHD and also in other areas (Barkmeier et al.,
2012a). Although the gold standard for interictal
spike detection has been and still mainly is a man-
ual evaluation, it has been shown that higher consis-
tency of results can be achieved by automated detec-
tion algorithm (Barkmeier et al., 2012b). Detection
algorithms can save enormous amount of work for re-
viewers and provide a faster data analysis for research
or even clinical practice.
2 OBJECTIVES
Computational efficiency is not so important when
recordings are processed from only a few channels
and a real-time detection is not necessary. Example of
those would be recordings from rodents (Ovchinnikov
et al., 2010). However, when processing intracranial
recordings from humans, in as much as 150 channels
with 5 kHz sampling rate, which are in average 30
minutes long, computational time requirements gain a
great deal of importance. While several terabytes (just
our institution) of such recordings are available for
processing, a detection algorithm has to be designed
to allow fast offline processing of intracranial record-
ings or even a real-time detection over at least hun-
dreds of channels simultaneously. In order to process
large signal data, the memory access is often a cru-
cial bottleneck for CPU processing, which puts high
requirements on effective cache utilization, to reduce
the access frequency to a slow main memory. The
goal of this paper is to propose an efficient spike de-
tection algorithm, particularly, the first level detector.
3 METHODS
3.1 Data Acquisition
Signal data which have been used for evaluation of
this detection algorithm were recorded from patients
suffering from pharmaco-resistant form of epilepsy.
The areas of brain where stereo electrodes have been
positioned vary through patients. This variability of
signal source is useful for algorithm testing, providing
a complex good-quality dataset. Signals have been
recorded approximately for 30 minutes each in 129 -
150 channels. Recordings also contain 6 non-iEEG
channels such as ECG, EOG, and calibration signals,
which can be omitted from processing. The recording
device records the data with 25 kHz sampling rate,
subsequently down-sampling them into 5 kHz range,
which is still relatively high, but it is necessary for
detection of other possible biomarkers, such as HFOs.
To illustrate the enormous size of such data
recordings, the channel size is expressed as:
channel size = 5000Hz*(30min * 60sec)* 4bytes
where the average recording file contains 150 such
channels, resulting into the file size of 5.4 GB, which
can be estimated by the following formula:
file size = 36MB * 150channels
Recordings of intracranial EEG are huge files and ter-
abytes of such data are available for processing (just
at our institution), which should be done by the pro-
posed algorithm for one 5 GB file in tens of seconds
instead of tens of minutes, as it has been done before.
3.2 Detection Algorithm
The detection algorithm has been designed to be mod-
ular, thus allowing the choice of how many modules
will be employed in detection. This approach en-
ables a direct implementation using the principles of
Kesner, F., Cimbalnik, J., Dolezalova, I., Brazdil, M. and Sekanina, L..
Fast Automated Interictal Spike Detection in iEEG/ECoG Recordings - {{\}it Using Optimized Memory Access}.
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

pipeline processing. It also offers a possibility to reg-
ulate the computational time needed for processing.
The following description will be devoted to a key
component of the algorithm - first level detector. The
algorithm has been designed to be cache-effective in
order to achieve a high processing speed, which is
relatively rare in these types of algorithms (Ovchin-
nikov et al., 2010). Since an amount of data to be
processed is enormous, re-iterating through large data
arrays in memory, in which signals are stored, would
lead to a high cache miss ratio. In order to develop
a cache-effective algorithm, the algorithm is never re-
iterating through the signal array. All operations are
performed on signal data, when they come, sample
by sample. This approach was also used in order to
provide the real-time processing capability, which is
discussed later in this paper.
When the first signal sample comes in, it is fil-
tered by a ’spike band’ filter group (band pass 20-50
Hz) providing one spike band sample. This filtered
sample may then be stored in a rotational buffer of
specified size (by parameter) or just used for com-
putation of adaptive min-max difference and then
dropped. Then the same signal sample (already stored
in cache/register) is filtered again, this time by the sec-
ond filter group (band pass 1-35 Hz) providing one
’enhanced band’ signal sample. This filtered sample
has to be stored in the rotational buffer of specified
size (by parameter) if the second level detection is ac-
tivated. Rotational buffers are computationally much
more effective than array shifting. They also increase
the cache-hit ratio and decrease memory requirements
compared to the block-processing oriented approach.
Compared to Barkmeier’s algorithm (Barkmeier
et al., 2012b), which uses the same frequency fil-
tration bands, in this case, only one-directional fil-
ters have been used instead of Matlab filtfilt()
function, which filters the signal from the left to the
right and subsequently from the right to the left in or-
der to eliminate phase delay, caused by filtration.
In our algorithm, phase delay caused by filters is
eliminated after the final detection step by subtracting
an empirical constant from the final top and border
indexes of detected spike.
After each filtered sample is obtained by ’spike
band’ filters, recent minimum and recent maximum
are estimated. Recent, or in other words, ’adaptive’
in this case means, that it represents the maximum or
minimum value in recently processed signal samples
(not associated with the rotational buffer size in any
way). This ’recentness’ is acquired by decay of these
values. The intensity of decay is one of the parameters
for first level detection and it should be chosen based
on the sampling rate and amplitude scale of the signal.
After every sample is processed, these ’recent’ values
are diminished by decay parameter, either by subtrac-
tion or multiplication by parameter ≤ 1.0. Then the
recent minimum-maximum difference is computed.
When this min-max difference rises over a specified
threshold, then it is recognized as a rising edge event
and detected by the first level method. Falling edge is
ignored. The illustration can be seen in Figure 1.
In order to avoid overlapping detections, possibly
of the same spike, the parameter of minimal distance
between rising edges is used.
Figure 1: Illustration of first level detection method: B2 is a
regular signal channel with two detected spikes; ’enhanced
band’ is filtered by bandpass 1-35 Hz; ’spike band’ is fil-
tered by bandpass 20-50 Hz; min-max rising edge illustrates
threshold crossing points.
4 RESULTS
Papers dealing with spike detection methods don’t
often mention real computational time requirements
for signal processing (Lodder et al., 2013)(Barkmeier
et al., 2012b). However, it is one of the most essen-
tial parameters for spike detection algorithm evalua-
tion, when huge recording files are being processed.
Computational time results of our first level detection
algorithm can be seen in Table 1. Measurements have
been done on HP Z420 workstation equipped with In-
tel(R) Xeon(R) CPU E5-1620.
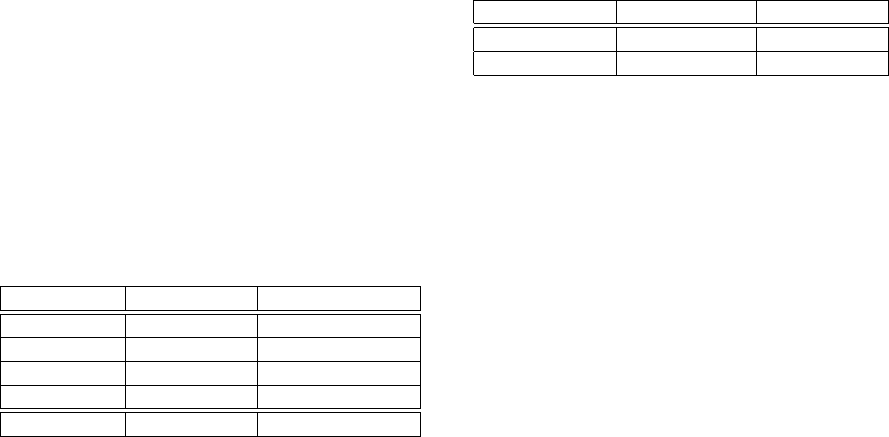
Table 1: Algorithm speed / computational time measured on
35 minute file recorded with 5 kHz sampling rate consisting
of 150 channels. Data loading time from harddrive is not
included in the computing time, as these operations can be
overlapped.
CPU threads proc. time [s] sig./comp. t.
1 50.722 37.426
2 55.757 34.046
4 50.019 37.952
8 28.798 65.918
data loading 25.239 ← for illustration
4.1 Detection Sensitivity and Precision
A golden standard for spike detection practically does
not exist. As has been shown (Barkmeier et al.,
2012b), the inter-reviewer variability is huge. In or-
der to at least partially suppress this inter-reviewer
variability and also overlooking spikes, signals were
reviewed by a two member group of biomedical en-
gineers and only detections where full agreement was
achieved have been considered. Detections made by
this algorithm have been visualized into the signal
window by half-transparent marks. The group of re-
viewers has been counting missed spikes into one cat-
egory (false negatives), spike-free detections into an-
other (false positives) and correct detections (true pos-
itives) separately. The number of true negatives would
be hard to estimate because it is the rest of the signal
without marks. Computed precision and sensitivity
based on the preliminary evaluation are presented in
Table 2. According to these results, the algorithm per-
forms quite well, reaching sensitivity 86 - 97 % and
precision 95-99 %.
5 DISCUSSION
Original Barkmeier’s algorithm (Barkmeier et al.,
2012b) running in Matlab, takes on average 32 min-
Table 2: First level detector sensitivity and precision based
on preliminary testing over 3 different patients, where fre-
quently spiking channels consisting of 4x 35 minutes have
been in or adjacent to seizure onset zone, and rarely spiking
channels consisting of 15 x 35 minutes have been outside of
this area.
signal sensitivity [%] precision [%]
rare. spik. chs. 86.463 95.652
freq. spik. chs. 97.831 99.628
utes to process the 35 minutes long file. Our highly
optimized re-implementation of Barkmeier’s algo-
rithm in C, which has been created for fairness of
comparison, is approximately 8 times faster. Com-
pared to these implementations, this new first level
detection algorithm implemented in C requires on av-
erage only 50 seconds running on the same hardware.
5.1 Real-time Detection
The algorithm has been designed with capability of
running the real-time detection. Hence this first level
detector does not see practically any ’future’ signal
samples to perform a successful detection. The pos-
sible second level detection, that will be developed,
in order to compute spike features may need about
40-80 ms of ’future’ signal after the first level detec-
tion. The algorithm has also been designed to keep the
computational time requirements minimal. In order
to illustrate how much computational time is needed
for a piece of signal, the signal-time / computational-
time ratio is presented in Table 1. It can be seen that
even without employing parallel computing for a 150
channel file with 5 kHz sampling rate, about 37-times
more channels can be processed while still perform-
ing in real-time. In theory it resulted in real-time pro-
cessing at 5550 channels.
ACKNOWLEDGEMENTS
This work was supported by Brno University of Tech-
nology grant under number FIT-S-14-2297 and by the
European Regional Development Fund the FNUSA-
ICRC project (No. CZ.1.05/1.1.00/02.0123).
REFERENCES
Barkmeier, D., Senador, D., Leclercq, K., and et al. (2012a).
Electrical, molecular and behavioral effects of inter-
ictal spiking in the rat. Neurobiology of Disease,
47(1):92–101.
Barkmeier, D., Shah, A., Flanagan, D., and et al.
(2012b). High inter-reviewer variability of spike de-
tection on intracranial eeg addressed by an automated
multi-channel algorithm. Clinical Neurophysiology,
123(6):1088–1095.
Lodder, S., Askamp, J., and van Putten, J. (2013). Inter-ictal
spike detection using a database of smart templates.
Clinical Neurophysiology, 124(12):2328–2335.
Ovchinnikov, A., Luttjohann, A., Hramov, A., and van Lui-
jtelaar, G. (2010). An algorithm for real-time detec-
tion of spike-wave discharges in rodents. Journal of
Neuroscience Methods, 194(1):172–178.
Staley, K., White, A., and Dudek, F. (2011). Interictal
spikes: harbingers or causes of epilepsy? Neuro-
science letters, 497(3):247–250.
