The Flows of Concepts
Marcin Skulimowski
Faculty of Physics and Applied Informatics, University of Lodz, Pomorska 149/153, 90-236 Lodz, Poland
Keywords:
Citation Relation, Semantic Publishing, Digital Libraries.
Abstract:
A scientific citation is usually presented as a relation between two publications without any precise meaning
and inner structure. In fact, the structure of a citation, which is usually not represented explicitly, can be
quite complex. Expanded citations, which link scientific papers and concepts from them, allow to represent
the structure in a machine-readable way. In this paper, we use expanded citations to introduce the notion of
concept flow. We briefly explore the notion and show that it opens interesting possibilities as far as concepts
and their importance in scientific domains are considered.
1 INTRODUCTION
A scientific citation is a relation between two scien-
tific publications (Egghe and Rousseau, 1990).
1
It
can be represented by an arrow from a node repre-
senting citing publication to a node representing cited
publication. The picture may suggest that a citation
is merely a relationship without any precise meaning
and inner structure. This is true, but only when we
”look” at a citation from a distance, so that the de-
tails disappear. However, if we read a paper we can
look at citations from the paper more closely. Then
we are able to add meaning to arrows representing
citations. Moreover, it is also possible to represent
the meaning in a machine-readable way (J¨org, 2008;
Teufel et al., 2006). An example worth mentioning is
CiTO, the Citation Typing Ontology which enables to
describe in RDF (Resource Description Framework)
the nature of bibliographic citations (Peroni and Shot-
ton, 2012). According to the best knowledge of the
author, previous works have only focused on the pre-
cise description of relations between scientific papers.
In our opinion, the structure of a citation can be de-
scribed more accurately. After reading two papers we
know which entities from a cited publication are used
in a citing publication and how they are used. Con-
sequently, we are able to name relations between en-
tities and publications. In this way we get to know
the structure of a citation which usually is not rep-
1
Our considerations apply to any type of scientic pub-
lication. The publications will also be referred to (inter-
changeably) as papers or articles. We do not distinguish
between them.
resented in an explicit form and, moreover, it can-
not be processed by machines. Indeed, until recently,
such a representation has not been possible. Nowa-
days, using the technologies of Semantic Web we
are able to represent the structure of a citation in a
machine-readable way. This can be done, for exam-
ple, by the creation of the so-called expanded cita-
tions which link not only publications but also enti-
ties from them (Skulimowski, 2014b). As a result, the
structure of a citation becomes represented explicitly
in machine-readable way. This leads to new oppor-
tunities as far as the processing of citations is con-
cerned. In particular, a new approach to processing
relationships between scientific publications and con-
cepts will become available. For example, the RDF
data obtained from expanded citations will enable us
to obtain answers to specific questions (represented
as SPARQL queries) concerning publications and en-
tities contained therein (Skulimowski, 2014a).
In this paper, we are looking ahead and assume
that expanded citations are commonly used among
scientific community. Consequently, we have ac-
cess to a huge concept network i.e. a graph struc-
ture containing publications and entities (concepts)
linked by relations represented by object properties
(Skulimowski, 2013). The properties can be seen as
supports of this structure. The aim of this paper is to
propose and consider a new approach to properties.
Our idea is the following: a scientific citation A → B
(A cites B) suggests that some entity from B (e.g. a
concept, formula, definition or some piece of data) is
somehow ”used” in A. We can say that the entity flows
from B to A. Consequently, we propose to treat prop-
292
Skulimowski, M..
The Flows of Concepts.
In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 3: KMIS, pages 292-298
ISBN: 978-989-758-158-8
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

erties as pipes or tubes through which concepts can
flow. These pipes we will call concept pipes. What is
important the flow through a concept pipe related to
an object property p depends on the meaning (seman-
tics) of p. We show in this paper that the approach
outlined above opens interesting possibilities as far as
concepts and their importance in scientific domains
are considered. The paper is organized as follows. In
Section 2 we have compiled some basic facts about
expanded citations and links between concepts. Sec-
tion 3 explains the idea of concept flows and intro-
duces the notion of a concept pipe. In Section 4 we
introduce and explain the notion of the projection of
a concept. The notion is then used in the proposed
definition of the concept flow. The paper ends with
discussion and the outline of future work.
2 EXPANDED CITATIONS
We say that a citation can be expanded(is expandable)
when its structure can be represented in a machine-
readable way. In order to present the definition of
expanded citation in details we need the notion of a
concept (Skulimowski, 2014b).
Definition 1. A concept is any entity (part) of a sci-
entific article named with a URI (Uniform Resource
Identifier).
A URI for an entity from a publication can be
obtained very easily by the concatenation of a URL
of the publication (
URL ), sharp ( # ) and a local name
of this entity (
LocalName ) i.e. URL#LocalName .
Example 1.
URIs of two different concepts:
http://onlinelibrary.wiley.com/doi/10.
1111/j.1365-2699.2008.02023.x#
microrefugium
http://www.cambridge.org/9780521701655#
Figure_1_1
In the rest of this paper, we treat a scientific pub-
lication (with some obvious simplification) as a set
of concepts contained in it. The set of all concepts
we denote by Conc. Moreover, we assume that in
some cases it is possible to link two concepts by an
object property defined in some vocabulary (ontol-
ogy). The set of all such properties we denote by
Prop. Note that, both sets Conc and Prop are ob-
viously finite. However, the set Conc is much more
numerous than Prop. A scientific publication may
contain multiple concepts. In turn, the set Prop can-
not be too broad because too large number of prop-
erties (representing relations) may hamper their use.
Now, we can give the definition of expanded citation
(Skulimowski, 2014b).
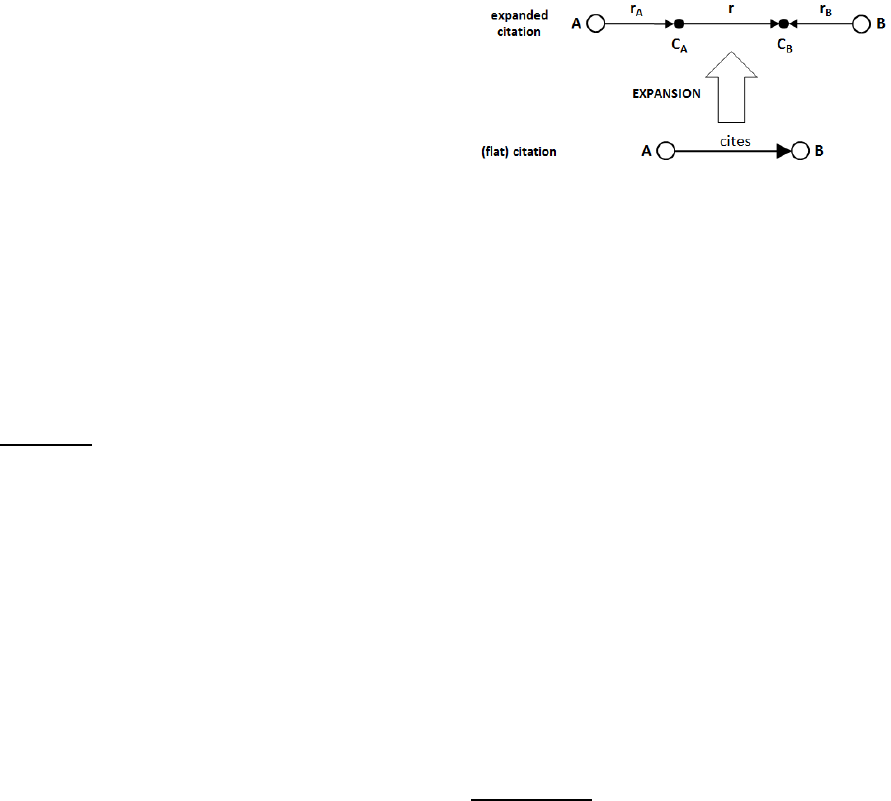
Definition 2. Let A and B be two publications. We
say that a citation A → B (A cites B) is expandable
if there exist concepts C
A
(from A) and C
B
(from B),
relations r, r
A
, r
B
∈ Prop represented by object prop-
erties from some ontology (ontologies) and the follow-
ing RDF statements
2
:
C
A
r C
B
. (1)
A r
A
C
A
. (2)
B r
B
C
B
. (3)
The set of triples (1-3) we will call an expanded cita-
tion (see Fig. 1).
Figure 1: The expansion of a flat citation ( - publications,
• - concepts) (Skulimowski, 2014b).
We allow that A refers directly to C
B
or to C
A
which
is identical to C
B
(we can use
owl:sameAs
3
). For
clarity reasons, in the rest of this paper standard cita-
tions will be called flat citations. In the cases when a
flat citation has a few reasons, we may create a few
expanded citations for it. They all form the struc-
ture of a citation which describes precisely a relation
between two publications. This (local) structure is
a part of a global structure called concept network
(Skulimowski, 2013). Figure 2 presents a concept
network created for 4 publications A, B,C and D. The
network consists of 8 expanded citations (the names
of relations are omitted for simplicity reasons). As
shown in the figure the network contains linked con-
cepts and publications. What is very important, is
that each link has a precise meaning. Thanks to that,
concepts are no longer locked in ”publication silos”.
They can be linked to other concepts and publications.
In the remainder of this paper we omit nodes corre-
sponding to publications and restrict our attention to
relations (links) between concepts.
Let C ∈ Conc. Other concepts can be directly linked
to C.
2
Throughout this paper, we use simplified Notion 3 syn-
tax for RDF (see http://en.wikipedia.org/wiki/Notation3).
For simplicity reasons, we use letters for resources.
3
http://www.w3.org/TR/owl-ref/#sameAs-def
The Flows of Concepts
293

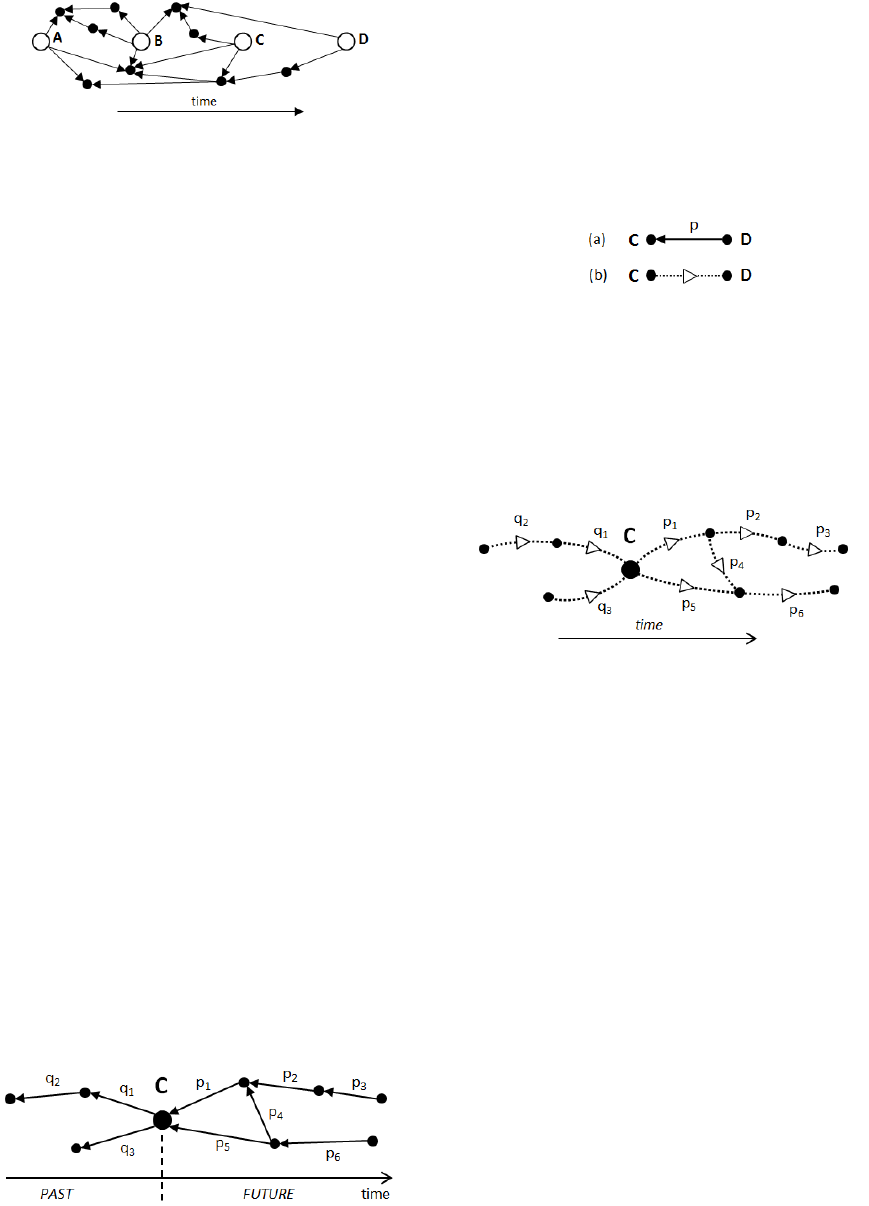
Figure 2: Concept network for 4 publications ( - publica-
tions, • - concepts; the names of relations are omitted).
Definition 3. We say that a concept D ∈ Conc is di-
rectly linked to C ∈ Conc if there exists p ∈ Prop such
that:
D p C.
We denote this relation by D ⇒ C.
Concepts do not need to be connected directly.
Definition 4. We say that a concept D ∈ Conc is
linked to C if D ⇒ C or if there existC
1
, ..., C
n
∈ Conc,
where n ≥ 1 such that:
D ⇒ C
1
⇒ C
2
... ⇒ C
n
⇒ C
We denote this relation by D → C.
By the reflexivity of the property p =
owl:sameAs
(McCusker and McGuinness, 2010), we have
C owl:sameAs C for C ∈ Conc. Thus the relation →
is reflexive. Moreover, it is easy to see that it is also
transitive. Thus, the following lemma is true.
Lemma 1. The relation → in Conc is reflexive and
transitive i.e. it is a preorder.
3 CONCEPT PIPES
Let us now consider a ”neighborhood” of a concept
C ∈ Conc i.e. (1) concepts to which C is linked,
(2) concepts linked to C and (3) object properties
related to these links. Such a ”neighborhood” of C
we will call shortly a C-network (see Fig. 3). It can
be easily seen, that a C-network can be divided into
two parts: past and future. Concepts from the future
are linked to C and C is linked to concepts from the
past (see Fig. 3). A C-network is not static, it evolves
and changes. It grows over time with new concepts
which are successively linked to old concepts as new
publications appear. One can say that properties
Figure 3: C-network is a network of linked concepts cen-
tered around C.
representing these links support the structure of a
C-network (and, in general, a concept network). In-
deed, the properties can be treated as supports of this
structure. In this article, we want to propose a slightly
different approach. Namely, we propose to treat
properties linking concepts as pipes or tubes through
which concepts can flow. The direction of this flow
is opposite to the directions of arrow representing
these properties in RDF. Consequently, an object
Figure 4: (a) RDF link between D and C (b) The flow from
C to D.
property represented by an arrow from the right to
the left we treat as a one-way concept pipe allowing
the flow of a concept in the opposite direction (see
Fig. 4). Thus, C ∈ Conc may flow only to concepts
from its future because they are connected to C (see
Fig. 5). In general, a concept may remain in place or
Figure 5: C-network and related flows of concepts.
flow. A concept of little importance or interest in a
scientific domain remains in place. Such a concept is
not connected to any concept pipe and therefore it has
nowhere to flow. On the other hand some concepts
are of great interest and importance in a domain.
They are ”used” in other concepts and publications.
In other words they flow to other concepts through
concept pipes created by properties. Now, the point
is that the flow of a concept depends on concept
pipes (object properties) connecting concepts. We
can say that C ∈ Conc flows to a publication A when
the concept is somehow ”used” in A. On the other
hand the flow of C is limited or even stopped when a
publication A contains any objections to this concept.
Consequently, some concept pipes favour the flow
(e.g. uses) other restrict the flow (e.g. contradicts).
In general, we assume that from the point of view of
the author of some concept a concept pipe may have
neutral, positive or negative influence on the concept
flow. This is very important assumption. Although,
at this time we do not know the whole set Prop, we
assume that properties from Prop can be reasonably
divided into the above three categories.
KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing
294

Example 2. Let us now consider the following set of
properties: {sameAs, use, generalizes, contradicts,
disputes, confirms}⊆Prop. We are going to determine
what is the influence of concept pipes corresponding
to these terms on a concept flow. To this end, let us
assume that at the beginning of a concept pipe there
is some C ∈ Conc and at the end there is some other
D ∈ Conc. What can we say about the flow of C
through the above pipes? In order to answer the ques-
tion we have to consider the nature of relationship be-
tween C and D. It obviously depends on the meaning
of an object property linking C and D. Recall that, we
consider the issue from the point of view of an author
of C.
• sameAs – in this case at the beginning and at the
end of the pipe is the same concept. Consequently,
we can say that C flows through this pipe un-
changed. So it is reasonable to assume that this
concept pipe is neutral to the flow of a concept.
• uses - the relation uses we understand as follows:
we say that D uses C when C is a part of D. This
definition can be adopted to many cases e.g.: a
mathematical formula D uses a concept C, a plot
D uses data from a tableC, a method D uses an al-
gorithm C. In all these cases, at the beginning and
at the end of this concept pipe there are two differ-
ent concepts. However, D in some sense contains
C. In other words, C flows to D. Consequently, we
assume that the influence of this property is posi-
tive. In fact, the influence is more positive than in
the case of sameAs property - C not only appears
in another article but is also used to obtain some
new concept D.
• generalizes – the meaning of this term is the fol-
lowing: D generalizes C when D is broader or
more general than C. We assume that the influ-
ence of this pipe is positive.
• contradicts - D contradicts or denies C. In other
words there is a direct opposition between D and
C. Thus in this case at the beginning and at the
end of the pipe there are two contrary concepts.
We can say that this pipe stops the flow of C. We
therefore assume that the influence of this concept
pipe is negative.
• disputes - in this case a concept D calls into ques-
tion C. We therefore assume that the influence of
this tube is also negative. However, we may as-
sume that it is less negative than in the case of
contradicts property.
• confirms - in this case a concept D confirms
(agrees with) C. We assume that the influence of
this pipe is positive.
In the above example we have divided the properties
into three categories (negative, neutral, positive) ac-
cording to their ”influence” on the concept flow. The
division into these categories seems to be sufficient in
the case of a simple set of properties. A more numer-
ous set Prop may require more precise description of
the influence of concept pipes. It can be done, for
example, by assigning a numerical value to each con-
cept pipe. This numerical value we will call a con-
cept flow index (in short CF). To obtain a value of
CF for each property we have to define a function
CF : Prop → R . We do not require that CF has to
be a one-to-one function (injection). It is important
for us that the values ofCF for various properties can
be compared. At present, we do not know the whole
set Prop. However, we assume that it is possible to
define a function CF satisfying:
CF|
negative
≤ CF|
neutral
≤ CF|
positive
Moreover, we also assume that CF is constant for
neutral properties. We denote this value of CF by
α
neut
.
Example 3.
Let us define CF for properties
from Example 2. In the case of neutral influ-
ence a concept pipe does not change the flow.
We put CF(sameAs) = 1.0. To the pipes with
positive influence we assign values greater than
1: CF(generalizes) = 1.8, CF(uses) = 1.5,
CF(confirms) = 1.2. Finally, to the pipes with
negative influence we assign values lower than 1:
CF(disputes) = 0.5, CF(contradicts) = 0.
In Example 3 a value of CF depends only on
the concept pipe. However, the value may also
depend on the type of a flowing concept. Moreover,
it is worth noting that assigning the value of CF to
each p ∈ Prop seems quite easy when we consider
rhetorical properties (e.g. confirms, corrects). How-
ever, in the case of more technical properties (e.g.
isRegulationOf, measures) this assignment is not so
obvious. A solution is to assume that the properties
of this kind are neutral to the flow. Finally, note also
that thanks to a function CF the set Prop becomes
preordered.
Example 4.
Let us consider the following links
between concepts.
<http://link.springer.com/article/
10.1007%2Fs10814-010-9045-7#Fig_3>
:uses
<http://www.lcoastpress.com/book.php?
id=253#Fig_2_17> .
<http://link.springer.com/article/
The Flows of Concepts
295

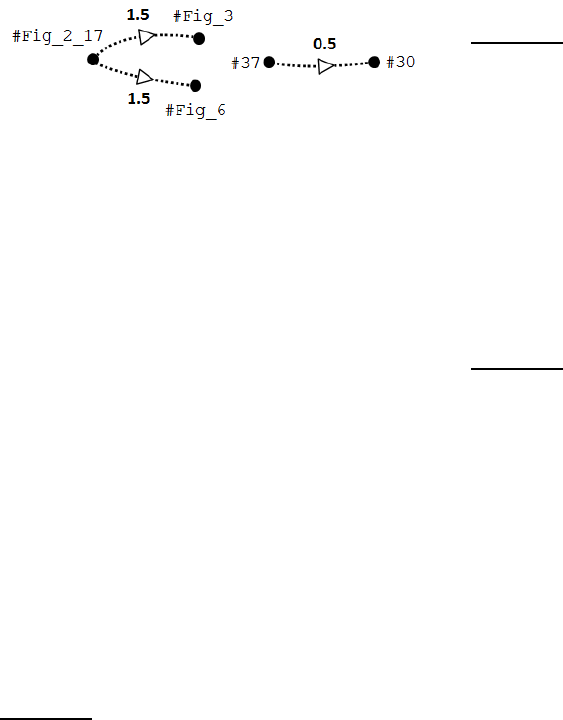
10.1007%2Fs10814-010-9045-7#Fig_6>
:uses
<http://www.lcoastpress.com/book.php?
id=253#Fig_2_17> .
<http://link.aps.org/doi/10.1103/
PhysRev.122.1649#30>
:disputes
<http://link.aps.org/doi/10.1103/
PhysRevA.54.4676#37>.
The flows corresponding to these links are presented
in Figure 6.
Figure 6: The flows of concepts (URI identifiers are short-
ened for clarity reasons).
Concept pipes enable flows of concepts between two
directly linked concepts. If we want to analyse flows
of concepts for longer distances we have to con-
sider connections of concept pipes. Let us now con-
sider two concept pipes corresponding to properties
p
1
, p
2
∈ Prop. These two pipes can be connected to
obtain a concept pipeline. However, the connection
is not always possible. Concept pipes corresponding
to object properties p
1
and p
2
cannot be connected
if the domain of p
1
is disjoint with the range of p
2
i.e.: Ran(p
2
) ∩ Dom(p
1
) = ∅. The pipes p
1
and
p
2
can be connected only for concepts from the set
Ran(p
2
)∩Dom(p
1
) 6= ∅. In the case of p
1
, p
2
∈ Prop
for which domains and ranges are not specified the
connection is always possible (then we may assume
that Ran(p
2
) = Conc and Dom(p
1
) = Conc). Sum-
ming up the above considerations, we introduce the
following definition.
Definition 5. An n-tuple (p
1
, ..., p
n
) ∈ Prop
n
is
called a concept pipeline of length n if Ran(p
i+1
) ∩
Dom(p
i
) 6= ∅ for i = 1, ..., n− 1.
Example 5.
The domains and ranges of the properties
from Example 2 are not specified. Consequently, we
may assume that they are equal to Conc. Thus, any
tuple of these properties is a concept pipeline e.g.:
(uses, generalizes), (contradicts, uses), (sameAs,
generalizes, uses).
We already know that concept pipes have vari-
ous influences on the concept flow. The influence
of a concept pipeline will obviously depend on its
component concept pipes. We propose the following
definition:
Definition 6. The concept flow index (CF) for a con-
cept pipeline (p
1
, ..., p
n
) ∈ Prop
n
is defined as fol-
lows:
CF(p
1
, ..., p
n
) :=
n
∏
i=1
CF(p
i
)
The definition has very important consequences.
First of all, CF(p
1
, ..., p
n
) = 0 iff ∃p
k
CF(p
k
) = 0.
In other words the flow through a concept pipeline
is not possible if it contains a concept pipe stoping
the flow. Furthermore, the definition suggests that
α
neut
= 1 because a concept pipe p
i
with a neutral
influence does not change the value of CF(p
1
, ..., p
n
).
Example 6.
Let us compute the values of CF
for pipelines from Example 5.
• CF(uses, generalizes) = 1.5× 1.8 = 2.70
• CF(contradicts, uses) = 0 × 1.5 = 0
• CF(sameAs, generalizes, uses) = 1.0 × 1.8 ×
1.5 = 2, 70
It is worth noting that the ability to connect two
concept pipes does not mean that such pipes really
appear in practice. The widespread use of expanded
citations will give us knowledge about kinds of con-
cept pipes (and their lengths) appearing in different
areas of science.
Example 7.
Two RDF links between three con-
cepts in quantum mechanics:
<http://link.aps.org/doi/10.1103/
PhysRev.122.1649#30>
:disputes
<http://link.aps.org/doi/10.1103/
PhysRevA.54.4676#37>.
<http://link.aps.org/doi/10.1103/
PhysRevA.54.4676#37>
:isRegulationOf
<http://link.aps.org/doi/10.1103/
PhysRevA.54.4676#22>
Note the concept pipe (isRegulationOf, disputes).
4 CONCEPTS AND THEIR
FLOWS
In our previous paper we have proposed the notion
of a projection of a concept C ∈ Conc on an ob-
ject property p ∈ Prop (Skulimowski, 2014a). It is
a set denoted by p-C containing all publications P for
which RDF statement P p C exists. In this paper we
limit ourselves to RDF statements D pC whereC, D ∈
Conc and p ∈ Prop (see RDF statement (1) from Def-
inition 2). In particular, we are interested in flows of
KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing
296

C ∈ Conc to other concepts C
1
, C
2
, ..., C
n
∈ Conc (see
Fig. 7). Therefore, we introduce the following defini-
tion:
Definition 7. A projection of a concept C ∈ Conc on
a pipeline (p
1
, ..., p
n
) ∈ Prop
n
is a set denoted by
(p
1
, ..., p
n
)-C and defined as follows:
(p
1
, ..., p
n
)-C = {(C
1
, ..., C
n
) ∈ Conc
n
:
C
n
p
n
C
n−1
. C
n−1
p
n−1
C
n−2
. ... C
1
p
1
C.}
Figure 7: A concept C may flow through a pipeline
(p
1
, ..., p
n
) ∈ Prop
n
. An n-tuple (C
1
, ..., C
n
) ∈ Conc
n
be-
longs to the projection of C on this pipeline.
For a given C ∈ Conc and a pipeline (p
1
, ..., p
n
) ∈
Prop
n
the projection (p
1
, ..., p
n
)-C contains n-tuples
(C
1
, ..., C
n
) ∈ Conc
n
of concepts through whichC may
flow (see Fig. 7). It is easy to prove the following
lemma.
Lemma 2. If (p
1
, ..., p
n
)-C = ∅ then ∀(q
1
, ..., q
m
) ∈
Prop
m
(p
1
, ..., p
n
, q
1
, ..., q
m
)-C = ∅.
We already know that C ∈ Conc may remain in place
or flow. If C is not connected to any concept pipe then
it has nowhere to flow. We introduce the following
definition.
Definition 8. A concept C is called isolated if ∀p ∈
Prop p-C = ∅.
An isolated concept C has not been linked to any con-
cept yet. This can change in time because in the fu-
ture links from other concepts may appear (as new
publications appear). At first some p-C set will be-
come nonempty. After some time (p, q)-C 6= ∅ be-
comes true and so on. Let us assume then that for
C ∈ Conc and a pipeline (p
1
, ..., p
n
) ∈ Prop
n
we have
(p
1
, ..., p
n
)-C 6= ∅. ThenC is not isolated, it may flow.
The existence of a concept pipe starting at C is the
necessary condition of this flow. Is this a sufficient
condition? In Section 3 we have divided concepts into
three categories. In the case of concept pipes hav-
ing positive influence a conceptC is somehow used in
other articles. We can say that C flows into new ”ar-
eas” of a domain, it flows to other concepts. In the
case of concept pipes having negative influence it is
difficult to say something about such a flow. Indeed,
C does not flow to other concepts. On the contrary,
there appear objections to C or even a concept which
is in a contradiction with C. In order to formalise the
notion of the concept flow we propose the following
definition:
Definition 9. Let C, D ∈ Conc. We say that a concept
C flows to D if:
1. There exists a concept pipeline (p
1
, ..., p
n
) ∈
Prop
n
, where n ≥ 1 and (C
1
, C
2
, ..., C
n−1
) ∈
Conc
n−1
such that (C
1
, C
2
, ..., C
n−1
, D) ∈
(p
1
, p
2
, ..., p
n
)-C.
2. ∀p
i
from (p
1
, ..., p
n
) we have CF(p
i
) ≥ α
neut
.
Thus, C flows to D if all concept pipes included in
a pipeline connecting C and D have at least neutral
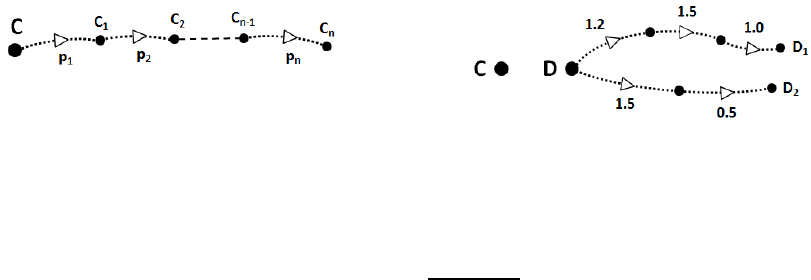
influence on the flow (see Fig. 8). A concept C which
Figure 8: An isolated concept C and not isolated concept D.
D flows to D
1
and does not flow to D
2
.
flows to some other concept we will call a flowing
concept.
Example 8.
In Example 7 we have the follow-
ing concept pipe: (isRegulationOf, disputes).
Assuming that CF(isRegulationOf) ≥ 1 and
CF(disputes) = 0.5 it follows that the concept
#22
flows to #37 and does not flow to #30 .
From the above considerations it follows that
concepts from Conc can be divided into two disjoint
categories: isolated (I) and not-isolated (NI). The
latter category can be further divided into two disjoint
subcategories: flowing (F) and not-flowing (NF).
Thus we obtain the following partition of Conc:
Conc = I ∪ NF ∪ F. The contents of these three sets
change over time. At first, a concept C belongs to I.
After some time there may appear a concept pipeline
starting at C. If it allows the flow (CF ≥ 1) then
C ∈ F if not then C ∈ NF. For many reasons the
category F is the most interesting. These concepts
are particularly important in a scientific domain. In
order to describe the importance of C ∈ Conc more
precisely we propose the following definition.
Definition 10. A range of C ∈ Conc denoted by R(C)
is the number of different concepts to which C flows.
The notion of range is related to the existence of a
function R : Conc → N which allows us to classify
concepts. The most important (influential) in a do-
main are flowing concepts with the highest values of
R. The least important are concepts with R(C) ≡ 0
(note that I ⊆ {C ∈ Conc : R(C) = 0}).
The Flows of Concepts
297

5 DISCUSSION AND FUTURE
WORK
Expanded citations allow us to represent in a
machine-readable way relations between concepts
and publications. The application of expanded ci-
tations leads to new opportunities as far as the pro-
cessing of the relations is considered (Skulimowski,
2014b; Skulimowski, 2014a). In this paper, we have
used expanded citations to consider the notion of the
concept flow.
Let us now shortly discuss the benefits of the pro-
posed approach. Suppose that we are interested in
some C ∈ Conc. Then, we can analyze flows of C.
In particular, we can find all concepts (and publica-
tions containing them) to which C flows. In this way
we obtain a knowledge about the importance of C in
a domain. Moreover, the knowledge of R allows us to
find concepts which are the most important in a given
scientific domain (these concepts flow to many other
concepts). It is worth noting that flows of C can be
visualized by graphs (see Fig. 9). This is very conve-
nient for scientists interested in a domain. The knowl-
edge about the influence of a concept and its flows to
other concepts could be used in the evaluation of sci-
entist’s work. Nowadays, in the evaluation the pres-
ence of a flat citation is taken into account (Egghe and
Rousseau, 1990). The structure of a citation and con-
cepts contained in it are not taken into account. How-
ever, a machine-readable representation of expanded
citations can make a difference. These issues require
further research.
The applications of expanded citations mentioned
in this and our previous papers (Skulimowski, 2014b;
Skulimowski, 2014a) become available provided that
expanded citations become popular among the sci-
entific community. Is it possible? Let us consider
the issue. The creation of expanded citations is ob-
viously more complicated and time-consuming pro-
cess than the creation of flat citations. While flat ci-
tations are very often created untidily, expanded ci-
tations requires more precision and additional knowl-
edge of relevant ontologies. It is not enough to create
a list of cited publications, the author has to link con-
cepts from his publication with previously published
concepts. We are of the opinion that expanded cita-
tion cannot be created in an automatic way. However,
the creation could be supported by some online tool.
But even then it will be a more demanding process
than the creation of flat citations. However, the ben-
efits arising from the use of expanded citations may
encourage the authors of publications to expand their
flat citations. It remains to be seen whether and how
the expanded citations will be used among the scien-
tific community. Maybe, in the near future expanded
citations might become a part of semantic publishing
(Shotton, 2009).
The results presented in this paper are encourag-
ing and suggest the following directions for future re-
search. First, we need to determine the set of proper-
ties Prop. To this end we are currently in the process
of developing SACO ontology containing terms used
in expanded citations
4
. The knowledge of Prop al-
lows us to define the function CF which is crucial for
the notion of concept flow. Second, in order to facil-
itate the creation of expanded citations we are going
to define precise and clear guidelines of how to create
expanded citations. Third, further work should target
the developing of a Web tool supporting the creation
of expanded citations. Finally, further work is also
needed to define measures of scientist’s work based
on expanded citations and the flows of concepts.
REFERENCES
Egghe, L. and Rousseau, R. (1990). Introduction to Infor-
metrics: quantitative methods in library, documenta-
tion and information science. Elsevier Science Pub-
lishers.
J¨org, B. (2008). Towards the nature of citations. In Pro-
ceedings of the 5th International Conference on For-
mal Ontology in Information Systems.
McCusker, J. P. and McGuinness, D. L. (2010). Towards
identity in linked data. In Proceedings of the 7th In-
ternational Workshop on OWL: Experiences and Di-
rections (OWLED 2010), San Francisco, California,
USA, June 21-22, 2010.
Peroni, S. and Shotton, D. (2012). FaBiO and CiTO: On-
tologies for describing bibliographic resources and ci-
tations. Web Semantics, 17:33–43.
Shotton, D. (2009). Semantic publishing: the coming rev-
olution in scientific journal publishing. Learned Pub-
lishing, 22(2):85–94.
Skulimowski, M. (2013). From linked data to concept net-
works. In Theory and Practice of Digital Libraries
2013, Communications in Computer and Information
Science, Vol. 416, pages 77–88.
Skulimowski, M. (2014a). Expanded citations and projec-
tions of concepts. In Proceedings of the 10th Interna-
tional Conference on Semantic Systems, SEMANTICS
2014, Leipzig, Germany, September 4-5, 2014, pages
73–76.
Skulimowski, M. (2014b). On expanded citations. In 14th
International Conference on Knowledge Management
and Data-driven Business, I-KNOW ’14, Graz, Aus-
tria, September 16-19, 2014, pages 38:1–38:4.
Teufel, S., Siddarthan, A., and Tidhar, D. (2006). An an-
notation scheme for citation function. In Proceedings
of 7th SIGdial Workshop on Discourse and Dialogue,
pages 80–87.
4
http://purl.org/lyr/saco
KMIS 2015 - 7th International Conference on Knowledge Management and Information Sharing
298