
Comparison of Data Selection Strategies for Online Support Vector
Machine Classification
Mario Michael Krell
1
, Nils Wilshusen
1
, Andrei Cristian Ignat
2,3
and Su Kyoung Kim
2
1
Robotics Research Group, University of Bremen, Robert-Hooke-Str. 1, Bremen, Germany
2
Robotics Innovation Center, German Research Center for Artificial Intelligence GmbH, Bremen, Germany
3
Jack Baskin School of Engineering, UC Santa Cruz, Santa Cruz, U.S.A.
Keywords:
Support Vector Machine, Online Learning, Brain Computer Interface, Electroencephalogram, Incremen-
tal/Decremental Learning.
Abstract:
It is often the case that practical applications of support vector machines (SVMs) require the capability to
perform online learning under limited availability of computational resources. Enabling SVMs for online
learning can be done through several strategies. One group thereof manipulates the training data and limits
its size. We aim to summarize these existing approaches and compare them, firstly, on several synthetic
datasets with different shifts and, secondly, on electroencephalographic (EEG) data. During the manipulation,
class imbalance can occur across the training data and it might even happen that all samples of one class are
removed. In order to deal with this potential issue, we suggest and compare three balancing criteria. Results
show, that there is a complex interaction between the different groups of selection criteria, which can be
combined arbitrarily. For different data shifts, different criteria are appropriate. Adding all samples to the pool
of considered samples performs usually significantly worse than other criteria. Balancing the data is helpful
for EEG data. For the synthetic data, balancing criteria were mostly relevant when the other criteria were not
well chosen.
1 INTRODUCTION
The support vector machine (SVM) has become a
well known classification algorithm due to its good
performance (Cristianini and Shawe-Taylor, 2000;
M
¨
uller et al., 2001; Sch
¨
olkopf and Smola, 2002; Vap-
nik, 2000). SVM is a static batch learning algorithm,
i.e., it uses all training data to build a model and does
not change when new data is processed. Despite hav-
ing the advantage of being a powerful and reliable
classification algorithm, SVM can run into problems
when dataset shifts (Quionero-Candela et al., 2009)
occur due to its static nature. The issues that arise
from dataset shifts are amplified when the algorithm
is run using limited resources, e.g., on a mobile de-
vice, because a complete retraining is not possible
anymore.
In the context of SVM learning applied to
encephalographic data (EEG), as used for brain-
computer interfaces (BCIs)(Blankertz et al., 2011;
Zander and Kothe, 2011; Kirchner et al., 2013;
W
¨
ohrle et al., 2015), dataset shifts are a major is-
sue. The source of the problem lies in the fact that
the observed EEG pattern changes over time, e.g., due
to inherent conductivity fluctuations, sensor displace-
ment, or subject tiredness. The issue of dataset shifts
also occurs in other applications like robotics. A clas-
sic example of a dataset shift would be that of a ma-
chine vision classifier being trained during daylight
and then used to classify image data taken during the
night. Temperature fluctuations, wear and debris in-
side the robotic frame can lead to a different behav-
ior in certain robotic systems. The behavioral change
then impacts measurement results, which is further re-
flected in the occurrence of a dataset shift.
In any case, it is often possible to adapt the clas-
sifier for new incoming data to handle continuous
dataset shifts. A straightforward approach would be
to integrate a mechanism that labels
1
the incoming
data, and afterwards retrain the SVM. Such a re-
1
When predicting movements with the help of EEG or
the electromyogram (EMG) in rehabilitation the labeling is
straightforward. For example, by means of a tracking de-
vice, or an orthosis, it can be checked whether there is a
“true” movement. After a short period of time, the data can
be labelled and used for updating the classifier.
Krell, M., Wilshusen, N., Ignat, A. and Kim, S..
Comparison of Data Selection Strategies for Online Support Vector Machine Classification.
In Proceedings of the 3rd International Congress on Neurotechnology, Electronics and Informatics (NEUROTECHNIX 2015), pages 59-67
ISBN: 978-989-758-161-8
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
59
training approach is used by (Steinwart et al., 2009),
whereby the optimization problem is given a warm
start. Note that there is a large corpus of other algo-
rithms to implement these strategies more efficiently
but they are not subject of this paper (Laskov et al.,
2006; Liang and Li, 2009). Nevertheless, there are
however computational drawbacks that come with
this approach, since the SVM update leads to an in-
crease in both processing time (especially when ker-
nels are used), as well as in memory consumption
which is the larger problem. Taking into account that
for applications like for example BCIs and robotics,
mobile devices are often used for processing (W
¨
ohrle
et al., 2013; W
¨
ohrle et al., 2014), the scarcity of
computing resources conflicts with a high computa-
tional cost. Additionally, the online classifier adap-
tation scheme should be faster than the time interval
between two incoming samples.
In the following, we focus on a small subgroup of
online learning algorithms which limit the size of the
training dataset, such that powerful generalization ca-
pabilities of SVM are not lost. In Section 2, we pro-
vide a systematic overview over the different strate-
gies for restricting the size of the training set. In the
context of data shifts, class imbalance is a major issue
which has not yet been sufficiently addressed for on-
line learning paradigms (Hoens et al., 2012). Hence,
we additionally suggest approaches which tackle this
specific problem, namely the case in which:
1. The class ratio is ignored.
2. After the initialization, the class ratio is kept fixed.
3. A balanced ratio is sought throughout the learning
process.
In Section 3, we provide a comparison of the numer-
ous strategies by testing them, firstly, on synthetic
datasets with different shifts and, secondly, on a more
complex classification task with EEG data. Finally,
we conclude in Section 4.
2 REVIEW OF TRAINING DATA
SELECTION STRATEGIES
This section introduces SVM and the different meth-
ods for manipulating its training data for online learn-
ing. The data handling methods for SVM can be di-
vided into criteria for adding samples, criteria for re-
moving samples, and further variants which influence
both.
2.1 Support Vector Machine
The main part of the SVM concept is the maxi-
mum margin which results in the regularization term
1
2
h
w, w
i
. Given the training data
D =
(x
j
,y
j
) ∈
{
−1,+1
}
× R
m
j ∈
{
1,...,n
}
,
(1)
the objective is to maximize the distance between two
parallel hyperplanes which separate samples x
i
with
positive labels y
i
= +1 from samples with negative
labels. The second part is the soft margin which al-
lows for some misclassification by means of the loss
term,
∑
t
j
. Both parts are weighted with a cost hy-
perparameter C. Since the data is usually normalized,
the separating hyperplane can be expected to be close
to the origin with only a small offset, b. Hence, the
solution is often simplified by minimizing b (Hsieh
et al., 2008; Mangasarian and Musicant, 1998; Stein-
wart et al., 2009). The resulting model reads:
min
w,b,t
1
2
k
w
k
2
2
+
1
2
b
2
+C
∑
t
j
s.t. y
j
(
w, x
j
+ b) ≥ 1 −t
j
,∀ j : 1 ≤ j ≤ n,
t
j
≥ 0 ,∀ j : 1 ≤ j ≤ n.
(2)
Here, w ∈ R
m
is the classification vector which, to-
gether with the offset b, defines the classification
function f (x) =
h
w, x
i
+ b. The final label is as-
signed by using the signum function on f . The de-
cision hyperplane is f ≡ 0, and the aforementioned
hyperplanes (with maximum distance) correspond to
f ≡ +1 and f ≡ −1. In order to simplify the con-
straints, and to ease the implementation of SVM, the
dual optimization is often used:
min
C≥α
j
≥0
1
2
∑
i, j
α
i
α
j
y
i
y
j
(k(x
i
,x
j
) + 1) −
∑
j
α
j
!
. (3)
The scalar product is replaced by a symmetric, posi-
tive, semi-definite kernel function k, which is the third
part of the SVM concept and allows for nonlinear sep-
aration with the decision function
f (x) =
n
∑
i=1
α
i
y
i
(k(x, x
i
) + 1) . (4)
A special property of SVM is its sparsity in the sam-
ple domain. In other words, there is usually a low
number of samples which lie exactly on the two sep-
arating hyperplanes (with C ≥ α
i
> 0), or on the
wrong side of their corresponding hyperplane (α
i
=
C). These samples are the only factors influencing the
definition of f . All samples with α > 0 are called
support vectors.
For the mathematical program of SVM, it can be
seen from its definition that all training data is re-
quired. When a new sample is added to the train-
ing set, the old sample weights can be reused and
NEUROTECHNIX 2015 - International Congress on Neurotechnology, Electronics and Informatics
60
updated; the fact that all the data is relevant is not
changed by a new incoming sample. In the case of
a linear kernel, one approach for online learning is
to calculate only the optimal α
n+1
if a new sample
x
n+1
comes in and leave the other weights fixed. This
update is directly integrated into the calculation of w
and b, and then the information can be removed from
memory, since it is not required anymore. The result-
ing algorithm is also called online passive-aggressive
algorithm (PA) (Crammer et al., 2006; Krell, 2015).
Another possibility is to add the sample, remove an-
other sample and then retrain the classifier with a lim-
ited number of iterations. The numerous existing cri-
teria for this manipulation strategies are introduced in
the following sections.
2.2 Inclusion Criteria (ADD)
The most common approach is to add all samples to
the training data set (Bordes et al., 2005; Funaya et al.,
2009; Gretton and Desobry, 2003; Oskoei et al., 2009;
Tang et al., 2006; Van Vaerenbergh et al., 2010; Van
Vaerenbergh et al., 2006; Yi et al., 2011). If the new
sample is already on the correct side of its correspond-
ing hyperplane (y
n+1
f (x
n+1
) > 1), the classification
function will not change with the update. When a
sample is on the wrong side of the hyperplane, the
classification function will change and samples which
previously did not have any influence might become
important. To reduce the number of updates, there are
approaches which only add the samples with impor-
tance to the training data. One of these approaches is
to add only misclassified samples (Bordes et al., 2005;
Dekel et al., 2008; Oskoei et al., 2009).
If the true label is unknown, the unsupervised ap-
proach by (Sp
¨
uler et al., 2012) suggests to use the im-
proved Platt’s probability fit (Lin et al., 2007) to ob-
tain a probability score from SVM. If the probability
exceeds a certain predefined threshold (0.8 in (Sp
¨
uler
et al., 2012)) the label is assumed to be true and the
label, together with the sample, are added to the train-
ing set. This approach is computationally expensive,
since the probability fit has to be calculated anew af-
ter each classifier update. Furthermore, it its quite in-
accurate, because it is calculated on the training data
(Lin et al., 2007). Note that, in this approach, sam-
ples within the margin are excluded from the update,
and that this approach does not consider the maxi-
mum margin concept of SVM.
In contrast to the previous approach, if the true
label is known, samples within the margin are espe-
cially relevant for an update of SVM (Bordes et al.,
2005; Oskoei et al., 2009); PA does the same intrinsi-
cally. Data outside the margin gets assigned a weight
of zero (α
n+1
= 0), and so the sample will not be in-
tegrated into the classification vector w. This method
is also closely connected to a variant where all data,
which is not a support vector, is removed.
In (Nguyen-Tuong and Peters, 2011) a sample is
added to the dataset if it is sufficiently linearly in-
dependent. This concept is generalized to classifiers
with kernels. In case of low dimensional data, this
approach is not appropriate, while for higher dimen-
sional data, it is computationally expensive. Fur-
thermore, it does not account for the SVM modeling
perspective where it is more appropriate to consider
the support vectors. For example, in the case of n-
dimensional data, n + 1 support vectors could be suf-
ficient for defining the separating hyperplane.
To save resources, a variant for adding samples
would be to add a change detection test (CDT), as an
additional higher-level layer (Alippi et al., 2014). The
CDT detects if there is a change in the data, and then
activates the update procedure. When working with
datasets with permanent/continuous shifts over time,
this approach is not appropriate, since the CDT would
always activate the update.
2.3 Exclusion Criteria (REM)
To keep the size of the training set bounded, in the
context of a fixed batch size, samples have to be re-
moved. One extreme case is the PA which removes
the sample directly after adding its influence to the
classifier. In other words, the sample itself is dis-
carded, but the classifier remembers its influence. If
no additional damping factor in the update formula is
used, the influence of the new sample is permanent.
In (Funaya et al., 2009), older samples get a lower
weight in the SVM model (exponential decay with a
fixed factor). This puts a very large emphasis on new
training samples and, at some stage, the weight for
the oldest samples is so low, that these samples can
be removed. In (Gretton and Desobry, 2003), the old-
est sample is removed for one-class SVM (Sch
¨
olkopf
et al., 2001). Removing the oldest sample is also
closely related to batch updates (Hoens et al., 2012).
Here, the classification model remains fixed, while
new incoming samples are added to a new training
set with a maximum batch size. If this basket is full,
all the old data is removed and the model is replaced
with a new one, trained on the new training data.
The farther away a sample is from the decision
boundary, the lower will the respective dual variable
be. Consequently, it is reasonable, to remove the far-
thest sample (Bordes et al., 2005), because it has the
lowest impact on the decision function f . If the sam-
ple x has the function value | f (x)| > 1, the respective
Comparison of Data Selection Strategies for Online Support Vector Machine Classification
61
weight is zero.
In the case of a linear SVM with two strictly sep-
arable datasets corresponding to the two classes, the
SVM can be also seen as the construction of a sepa-
rating hyperplane between the convex hulls of the two
datasets. So, the border points are most relevant for
the model, and might become support vectors in fu-
ture updates. Hence, another criterion for removing
data points is to determine the centers of the data and
remove all data outside of the two annuli around the
centers (Yi et al., 2011). If the number of samples
is to high, the weighted distance from the algorithm
could be used as a further criterion for removal. Al-
ternatively, we suggest to construct a ring instead of
an annulus, samples could be weighted by their dis-
tance to the ring and thus, be removed if they are not
close enough to the respective ring. Drawbacks of this
method are the restriction to linear kernels, the (often
wrong) assumption of circular shapes of the datasets,
and the additional parameters which are difficult to
determine.
Similar to the inclusion criterion, linear indepen-
dence could also be used for removing the “least lin-
early independent” samples (Nguyen-Tuong and Pe-
ters, 2011). This approach suffers from the drawbacks
of computational cost and additional hyperparame-
ters, too.
2.4 Further Criteria (KSV, REL, BAL)
As already mentioned, support vectors are crucial for
the decision function. A commonly used selection
criterion is that of keeping only support vectors (KSV)
(Bordes et al., 2005; Yi et al., 2011) and removing all
the other data from the training set.
While in the supervised setting, there might be
some label noise from the data sources, in the un-
supervised case labels might be assigned completely
wrong. For compensation, (Sp
¨
uler et al., 2012) sug-
gests to relabel (REL) every sample with the pre-
dicted label from the updated classifier. This ap-
proach is also repeatedly used by (Li et al., 2008) for
the semi-supervised training of an SVM.
Insofar, the presented methods did not consider
the class distribution. The number of samples of one
class could be drastically reduced, when the inclu-
sion criteria mostly add data from one class and/or the
exclusion criteria mostly remove data from the other
class. Furthermore, when removing samples, it might
occur that older data ensured a balance in the class
distribution while the incoming data belongs to only
one class. Hence, we suggest three different mantras
for data balancing (BAL). Don’t handle the classes
differently. Keep the ratio as it was when first filling
the training data basket, i.e., after the initialization al-
ways remove a sample from the same class type as
it was added in the current update step. For us, the
most promising approach is to strive for a balanced
ratio when removing data, by always removing sam-
ples from the overrepresented class.
Note that these three criteria can be combined with
each other, as well as with all inclusion and exclusion
criteria.
3 EVALUATION
This section describes an empirical comparison of a
selection of the aforementioned methods on synthetic
and EEG data. We start by describing the data gen-
eration (for synthetic data), or acquisition (for EEG
data). Afterwards, we present the processing methods
and describe the results of the analysis.
3.1 Data
For the synthetic data, we focus on linearly separa-
ble data. The first case that we consider is that of a
data shift which is parallel to the separating hyper-
plane (“Parallel”). In all the other cases, the decision
function is time dependent. Five datasets with differ-
ent shifts are depicted in Figure 1. The data was ran-
domly generated with Gaussian distributed noise and
shifting means. Since class distributions are usually
unbalanced in reality, we used a ratio of 1:3 between
the two classes, with the underrepresented class la-
beled as C2.
For a three dimensional example, we followed the
approach by (Street and Kim, 2001) in order to cre-
ate a dataset with an abrupt concept change every 100
samples, in contrast to the continuous shifts. The
data was randomly sampled in a three-dimensional
cube. Given a three dimensional sample (p
1
, p
2
, p
3
),
a two step procedure is implemented to define the
class label. For samples of the first class, initially,
p
1
+ p
2
≤ θ has to hold. Next, 10% class noise is
added for both classes. p
3
only introduces noise and
has no influence on the class. Theta is randomly
changed every 100 samples in the interval (6,14).
The six datasets have a total of 10000 samples.
Of these, the first 1000 samples are taken for training
and hyperparameter optimization while the remaining
9000 samples are used for testing. The same synthetic
data was used for all evaluations.
For real world, experimental data, we used data
from a controlled P300 oddball paradigm (Courch-
esne et al., 1977), as described in (Kirchner et al.,
NEUROTECHNIX 2015 - International Congress on Neurotechnology, Electronics and Informatics
62

x
2
x
1
C1
C2
(a) Parallel
x
2
x
1
C1
C2
(b) LinearShift
x
2
x
1
C2
C1
(c) Opposite
x
2
x
1
C2
C1
(d) Cross
x
2
x
1
C1
C2
(e) Parabola
Figure 1: Synthetic two-dimensional datasets with the classes C1 and C2 (underrepresented target class) with shifting Gaussian
distribution depicted by arrows.
2013). In the experimental paradigm, which is in-
tended for use in a real BCI, the subject sees an unim-
portant piece of information every second, with some
jitter. With a probability of 1/6, an important piece of
information is displayed, information which requires
an action from the subject. This task-relevant event
leads to a specific pattern in the brain, called P300.
The goal of the classification task is to discriminate
the different patterns in the EEG. In this paradigm it
is possible to infer the (probably) true label, due to the
reaction of the subject.
For the data acquisition process, we had 5 sub-
jects, with 2 recording sessions per subject. The
recording sessions were divided into 5 parts, where
each part yielded 720 samples of unimportant infor-
mation and 120 samples of important information.
For the evaluation, we used 1 part for training, and
the 4 remaining parts for testing.
3.2 Processing Chain and
Implementation
The chosen classifier was a SVM implementation
with a linear kernel, as suggested by (Hsieh et al.,
2008). We limited the number of iterations to 100
times the number of samples. The regularization hy-
perparameter C of the SVM was optimized using 5
fold cross validation, with two repetitions, and the
values [10
0
,10
−0.5
,...,10
−4
].
For the synthetic data as well as for the EEG data,
a normalization based on the training data was per-
formed, such that the dataset would exhibit a mean
µ = 0 and standard deviation σ = 1 for every feature.
In the case of the EEG data, further preprocessing was
done by means of a standard processing chain, as de-
scribed in (Kirchner et al., 2013).
For the evaluation part, each sample was first clas-
sified, and then the result was forwarded to the per-
formance calculation routine. Afterwards, the correct
label was provided to the algorithm for manipulating
the training data of the classifier, and, if necessary,
the classifier was updated. In order to save time, the
SVM was only updated when the data led to a change
which required an update. If, for example, data out-
side of the margin is added and removed, no update is
required.
A preceding analysis was performed on the syn-
thetic data to analyze the unsupervised label assign-
ment parameter (Sp
¨
uler et al., 2012). The analysis
revealed that all data should be added for the clas-
sification. Hence, we did not consider unsupervised
integration of new data any further. For comparison,
we used batch sizes [50,100,...,1000] for the syn-
thetic data and [100,200, . . . , 800] for the EEG data.
We implemented and tested the criteria “all”, “mis-
classified”, “within margin” for adding samples, “old-
est”, “farthest”, “border points” with tour variant for
removing samples and the (optional) variants to “rela-
bel” the data, “keep only support vectors”, and “data
balancing”.
2
For the details to the methods refer to
Section 2.
To account for class imbalance, we used balanced
accuracy (BA) as a performance measure (Straube and
Krell, 2014), which is the arithmetic mean of true pos-
itive rate, and true negative rate. As baseline classi-
fiers, we used online PA and static SVM.
We did not test an unsupervised setting for the
update of the classifier. In this case either semi-
supervised classifiers could be used or the classi-
fied label could be assumed to be the true label. In
the latter case, all aforementioned strategies could
be applied and the relabeling is especially important
(Sp
¨
uler et al., 2012). For classical BCIs the true
label is often not available, especially when using
spellers for patients with locked-in syndrome (Mak
et al., 2011). In contrast, with embedded brain read-
ing (Kirchner et al., 2014) the true label can be often
inferred from the behavior of the subject. If the sub-
ject perceives and reacts to an important rare stimu-
lus, the respective data can be labeled as P300 data.
For simplicity, the reaction in our experiment was a
buzzer press. Another example is movement predic-
tion where the true label can be inferred by other sen-
sors like EMG or force sensors. Supervised settings
should be preferred if possible because they usually
2
The code is publicly available, including the complete
processing script and the generators for the datasets at the
repository of the software pySPACE (Krell et al., 2013).
Comparison of Data Selection Strategies for Online Support Vector Machine Classification
63
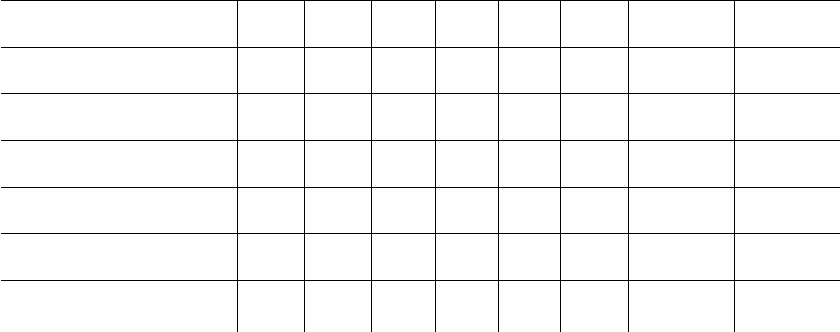
Table 1: Comparison of different data selection strategies for each dataset. For further details refer to the description in
Section 3.3.
DATASET ADD REM BAL KSV REL SIZE PERF SVM/PA
LinearShift m o n f f 1000 87.1 50.2
m o k - t 94.5
Parallel w n n f t 150 96.4 55.9
m f b f - 88.7
Opposite m f n - - 200 95.4 39.4
m o n f t 68.4
Cross m o n - - 150 95.2 55.7
m o b - - 67.6
Parabola a o k f t 50 96.8 66.2
m f, o b t t 61.3
3D (Street and Kim, 2001) a, w o n - - 50 87.7 81.1
w o n, b f - 51.0
EEG m f b f f 600 84.7 ± 0.3 83.7 ± 0.3
w o b f f
300,
400
84 ± 0.4
84.1 ± 0.3
83.0 ± 0.4
result in better performance.
3.3 Results and Discussion
For the synthetic data, the results were analyzed by
repeated measure ANOVA with 5 within-subjects fac-
tors (criteria): inclusion (ADD), exclusion (REM),
data balancing (BAL), support vector handling
(KSV), and relabeling (REL). For the EEG data, the
basket size was considered as an additional factor.
Here, we looked for more general good performing al-
gorithms independently from subject, session or repe-
tition. Where necessary, the Greenhouse-Geisser cor-
rection was applied. For multiple comparisons, the
Bonferroni correction was used.
In Table 1, the different strategies of how to
• ADD: all (a), within margin (w), misclassified (m)
and
• REMove: oldest (o), farthest (f), not a border
point (n) samples,
• for data BALancing: no handling (n), balancing
the ratio (b), or keep it fixed (k),
• Keeping only Support Vectors (KSV): active (t)
and not active (f), and
• RELabeling: active (t) and not active (f)
are compared. For each dataset, first the best combi-
nation of strategies with the respective batch size and
performance (balanced accuracy in percent) are given
based on the descriptive analysis. The performance
for SVM and PA are provided as baselines. In addi-
tion, the best strategy was selected separately for each
criterion which was statistically estimated irrespective
of the interaction between criteria (second row). In
case, that strategies of criteria did not differ from each
other, it is not reported (-).
Although the best approach is different depend-
ing on the dataset, some general findings could be ex-
tracted from descriptive and inference statistics.
First, for all datasets, the best combination of
strategies with a limited batch size outperformed the
static SVM and the PA except for the “LinearShift”
dataset (Table 1: first row). The SVM is static and
cannot adapt to the drift and the PA is adapting to
the drift but it does not forget its model modifications
from previous examples.
Second, specific approaches were superior com-
pared to other approaches (Table 1: second row). For
most cases, it was best to add only misclassified sam-
ples. A positive side effect of adding only misclas-
sified samples is the reduced processing time, due
to a lower number of required updates. Removing
the oldest samples often gave good results, because
a continuous shifts of a dataset leads to a shift of
the optimal linear separation function and older sam-
ples would violate the separability. Not removing the
border points showed bad performance in every case.
Mostly, balancing the data led to higher performance.
Often, the remaining two criteria had less influence
but there is a tendency for relabeling data and not
keeping only support vectors.
Third, the investigation of the interaction between
the criteria could help to understand why there is
some discrepancy between the best combination of
strategies (first row) and the best choice for each indi-
vidual criterion (second row). For example, if a good
joint selection of inclusion and exclusion criteria is
made, there are several cases where relabeling is no
longer necessary (possibly because the data is already
NEUROTECHNIX 2015 - International Congress on Neurotechnology, Electronics and Informatics
64

Figure 2: Comparison of all combinations of strategies from three different criteria (inclusion/exclusion/basket size) with
data balancing (BAL-b) but without relabeling (REL-f) or keeping more than just support vectors (KSV-f). The mean of
classification performance and standard error are depicted.
well separated), or the data should not have to be bal-
anced anymore (maybe because a good representative
choice is already made). Two more detailed examples
are given in the following.
For the “Opposite” dataset, the BAL criterion had
a clear effect. All combinations with not handling the
class ratios (BAL-n) were better than the other com-
binations with BAL-b and BAL-k. In contrast, the
KSV criterion had no strong effect. In combination
with KSV-t, removing no boarder points (REM-n)
improved the performance but the performance de-
creased for a few other combinations of in-/exclusion
criteria with KSV-t. On the other hand, the KSV cri-
terion had an interaction with the relabeling criterion
(REL). In combination with KSV-f, REL had no ef-
fect but REL-t improved performance for some com-
binations with KSV-t.
For the EEG data, the handling of support vec-
tor affected classification performance, i.e., the per-
formance was significantly worse when keeping only
support vectors (KSV-t) compared to keeping more
than just the support vectors (KSV-f). The effect of
the support vector handling dominated the other cri-
teria. The performance of combinations with KSV-f
was always higher than the combinations with KSV-t.
Thus, it makes less sense to choose the combina-
tions with KSV-t. The similar pattern was observed in
the handling of relabeling (REL) and data balancing
(BAL). When not relabeling the samples (REL-f) and
when keeping a balanced class ratio (BAL-b) the per-
formance was superior compared to other strategies
of REL and BAL. Hence, we chose a fixed strategy
of these three criteria (KSV-f, REL-f, BAL-b) for the
following visualization. Figure 2 illustrates the com-
parison of the respective combinations of criteria. The
best combination was obtained when combining the
inclusion of misclassified samples with the exclusion
of oldest or farthest samples for the basket size of 600.
This inclusion has a low number of updates. Imple-
menting the removal of oldest samples is straightfor-
ward whereas removing the farthest samples requires
some additional effort. Hence, these combinations are
beneficial in case of using a mobile device, which re-
quires a trade off between efficiency and performance.
4 CONCLUSION
In this paper, we reviewed numerous data selection
strategies and compared them on synthetic and EEG
data. As expected, we could verify that online learn-
ing can improve the performance. This even holds
when limiting the amount of used data. Depending
on the kind of data (shift), different methods are su-
perior. Considering that usually more data is expected
to improve performance or at least not to reduce it is
surprising that adding only misclassified data is often
a good approach and it is in most cases significantly
better than adding all incoming data. Furthermore,
this approach comes with the advantage of requiring
the lowest processing costs. Our suggested variant
of balancing the class ratios was beneficial in several
cases, but the benefit was dependent on the type of
the shift and the chosen inclusion/exclusion criterion,
Comparison of Data Selection Strategies for Online Support Vector Machine Classification
65
because some variants balance the data intrinsically,
or keep the current class ratio. Hence, it should al-
ways be considered, especially since it makes the al-
gorithms robust against long time occurrence of only
one class. Last but not least, we observed that it is al-
ways important to look at the interaction between the
selection strategies.
In future, we want to analyze different hybrid ap-
proaches between the selection strategies from SVM
and PA. Some inclusion strategies can be applied to
the PA and when removing samples from the training
set, their weights could be kept integrated into the lin-
ear classification vector. Additionally, we will com-
pare the most promising approaches on different data,
such as movement prediction with EEG or EMG,
and on different transfer setups which will come with
other kinds of data shifts. Last but not least, differ-
ent implementation strategies for efficient updates and
different strategies for unsupervised online learning
could be compared. In the latter, the relabeling cri-
terion is expected to be much more beneficial than in
our evaluation.
ACKNOWLEDGEMENTS
This work was supported by the Federal Min-
istry of Education and Research (BMBF, grant no.
01IM14006A).
We thank Marc Tabie and our anonymous review-
ers for giving useful hints to improve the paper.
REFERENCES
Alippi, C., Liu, D., Zhao, D., Member, S., and Bu, L.
(2014). Detecting and Reacting to Changes in Sensing
Units: The Active Classifier Case. IEEE Transactions
on Systems, Man, and Cybernetics: Systems, 44(3):1–
10.
Blankertz, B., Lemm, S., Treder, M., Haufe, S., and M
¨
uller,
K.-R. (2011). Single-Trial Analysis and Classifica-
tion of ERP Components–a Tutorial. NeuroImage,
56(2):814–825.
Bordes, A., Ertekin, S., Weston, J., and Bottou, L. (2005).
Fast Kernel Classifiers with Online and Active Learn-
ing. The Journal of Machine Learning Research,
6:1579–1619.
Courchesne, E., Hillyard, S. A., and Courchesne, R. Y.
(1977). P3 waves to the discrimination of targets in
homogeneous and heterogeneous stimulus sequences.
Psychophysiology, 14(6):590–597.
Crammer, K., Dekel, O., Keshet, J., Shalev-Shwartz, S., and
Singer, Y. (2006). Online Passive-Aggressive Algo-
rithms. Journal of Machine Learning Research, 7:551
– 585.
Cristianini, N. and Shawe-Taylor, J. (2000). An Introduction
to Support Vector Machines and other kernel-based
learning methods. Cambridge University Press.
Dekel, O., Shalev-Shwartz, S., and Singer, Y. (2008). The
Forgetron: A Kernel-Based Perceptron on a Budget.
SIAM Journal on Computing, 37(5):1342–1372.
Funaya, H., Nomura, Y., and Ikeda, K. (2009). A Support
Vector Machine with Forgetting Factor and Its Statis-
tical Properties. In K
¨
oppen, M., Kasabov, N., and
Coghill, G., editors, Advances in Neuro-Information
Processing, volume 5506 of Lecture Notes in Com-
puter Science, pages 929–936. Springer Berlin Hei-
delberg.
Gretton, A. and Desobry, F. (2003). On-line one-class sup-
port vector machines. An application to signal seg-
mentation. In 2003 IEEE International Conference
on Acoustics, Speech, and Signal Processing (ICASSP
’03), volume 2, pages 709–712. IEEE.
Hoens, T. R., Polikar, R., and Chawla, N. V. (2012). Learn-
ing from streaming data with concept drift and imbal-
ance: an overview. Progress in Artificial Intelligence,
1(1):89–101.
Hsieh, C.-J., Chang, K.-W., Lin, C.-J., Keerthi, S. S., and
Sundararajan, S. (2008). A dual coordinate descent
method for large-scale linear SVM. In Proceedings of
the 25th International Conference on Machine learn-
ing (ICML 2008), pages 408–415. ACM Press.
Kirchner, E. A., Kim, S. K., Straube, S., Seeland, A.,
W
¨
ohrle, H., Krell, M. M., Tabie, M., and Fahle, M.
(2013). On the applicability of brain reading for pre-
dictive human-machine interfaces in robotics. PloS
ONE, 8(12):e81732.
Kirchner, E. A., Tabie, M., and Seeland, A. (2014). Mul-
timodal movement prediction - towards an individual
assistance of patients. PloS ONE, 9(1):e85060.
Krell, M. M. (2015). Generalizing, Decoding, and Opti-
mizing Support Vector Machine Classification. Phd
thesis, University of Bremen, Bremen.
Krell, M. M., Straube, S., Seeland, A., W
¨
ohrle, H., Teiwes,
J., Metzen, J. H., Kirchner, E. A., and Kirchner, F.
(2013). pySPACE a signal processing and classifica-
tion environment in Python. Frontiers in Neuroinfor-
matics, 7(40):1–11.
Laskov, P., Gehl, C., Kr
¨
uger, S., and M
¨
uller, K.-R. (2006).
Incremental Support Vector Learning: Analysis, Im-
plementation and Applications. Journal of Machine
Learning Research, 7:1909–1936.
Li, Y., Guan, C., Li, H., and Chin, Z. (2008). A self-training
semi-supervised SVM algorithm and its application in
an EEG-based brain computer interface speller sys-
tem. Pattern Recognition Letters, 29(9):1285–1294.
Liang, Z. and Li, Y. (2009). Incremental support vector
machine learning in the primal and applications. Neu-
rocomputing, 72(10-12):2249–2258.
Lin, H.-T., Lin, C.-J., and Weng, R. C. (2007). A note
on Platts probabilistic outputs for support vector ma-
chines. Machine Learning, 68(3):267–276.
Mak, J., Arbel, Y., Minett, J., McCane, L., Yuksel, B., Ryan,
D., Thompson, D., Bianchi, L., and Erdogmus, D.
(2011). Optimizing the p300-based brain–computer
NEUROTECHNIX 2015 - International Congress on Neurotechnology, Electronics and Informatics
66
interface: current status, limitations and future direc-
tions. Journal of neural engineering, 8(2):025003.
Mangasarian, O. L. and Musicant, D. R. (1998). Successive
Overrelaxation for Support Vector Machines. IEEE
Transactions on Neural Networks, 10:1032 – 1037.
M
¨
uller, K.-R., Mika, S., R
¨
atsch, G., Tsuda, K., and
Sch
¨
olkopf, B. (2001). An introduction to kernel-based
learning algorithms. IEEE Transactions on Neural
Networks, 12(2):181–201.
Nguyen-Tuong, D. and Peters, J. (2011). Incremental online
sparsification for model learning in real-time robot
control. Neurocomputing, 74(11):1859–1867.
Oskoei, M. A., Gan, J. Q., and Hu, O. (2009). Adap-
tive schemes applied to online SVM for BCI data
classification. In Proceedings of the 31st Annual In-
ternational Conference of the IEEE Engineering in
Medicine and Biology Society: Engineering the Fu-
ture of Biomedicine, EMBC 2009, volume 2009, pages
2600–2603.
Quionero-Candela, J., Sugiyama, M., Schwaighofer, A.,
and Lawrence, N. D. (2009). Dataset Shift in Machine
Learning. MIT Press.
Sch
¨
olkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J.,
and Williamson, R. C. (2001). Estimating the support
of a high-dimensional distribution. Neural Computa-
tion, 13(7):1443–1471.
Sch
¨
olkopf, B. and Smola, A. J. (2002). Learning with Ker-
nels: Support Vector Machines, Regularization, Opti-
mization, and Beyond. MIT Press, Cambridge, MA,
USA.
Sp
¨
uler, M., Rosenstiel, W., and Bogdan, M. (2012). Adap-
tive SVM-Based Classification Increases Performance
of a MEG-Based Brain-Computer Interface (BCI).
In Villa, A., Duch, W.,
´
Erdi, P., Masulli, F., and
Palm, G., editors, Artificial Neural Networks and Ma-
chine Learning ICANN 2012, volume 7552 of Lecture
Notes in Computer Science, pages 669–676. Springer
Berlin Heidelberg.
Steinwart, I., Hush, D., and Scovel, C. (2009). Training
SVMs without offset. Journal of Machine Learning
Research, 12:141–202.
Straube, S. and Krell, M. M. (2014). How to evaluate
an agent’s behaviour to infrequent events? – Reli-
able performance estimation insensitive to class dis-
tribution. Frontiers in Computational Neuroscience,
8(43):1–6.
Street, W. N. and Kim, Y. (2001). A Streaming Ensemble
Algorithm (SEA) for Large-scale Classification. In
Proceedings of the Seventh ACM SIGKDD Interna-
tional Conference on Knowledge Discovery and Data
Mining, KDD ’01, pages 377–382, New York, NY,
USA. ACM.
Tang, H.-S., Xue, S.-T., Chen, R., and Sato, T.
(2006). Online weighted LS-SVM for hysteretic struc-
tural system identification. Engineering Structures,
28(12):1728–1735.
Van Vaerenbergh, S., Santamaria, I., Liu, W., and Principe,
J. C. (2010). Fixed-budget kernel recursive least-
squares. In 2010 IEEE International Conference
on Acoustics, Speech and Signal Processing, pages
1882–1885. IEEE.
Van Vaerenbergh, S., Via, J., and Santamaria, I. (2006). A
Sliding-Window Kernel RLS Algorithm and Its Ap-
plication to Nonlinear Channel Identification. In 2006
IEEE International Conference on Acoustics Speed
and Signal Processing Proceedings, volume 5, pages
789–792. IEEE.
Vapnik, V. (2000). The nature of statistical learning theory.
Springer.
W
¨
ohrle, H., Krell, M. M., Straube, S., Kim, S. K., Kirchner,
E. A., and Kirchner, F. (2015). An Adaptive Spatial
Filter for User-Independent Single Trial Detection of
Event-Related Potentials. IEEE transactions on bio-
medical engineering, PP(99):1.
W
¨
ohrle, H., Teiwes, J., Krell, M. M., Kirchner, E. A., and
Kirchner, F. (2013). A Dataflow-based Mobile Brain
Reading System on Chip with Supervised Online Cal-
ibration - For Usage without Acquisition of Training
Data. In Proceedings of the International Congress on
Neurotechnology, Electronics and Informatics, pages
46–53, Vilamoura, Portugal. SciTePress.
W
¨
ohrle, H., Teiwes, J., Krell, M. M., Seeland, A., Kirch-
ner, E. A., and Kirchner, F. (2014). Reconfigurable
Dataflow Hardware Accelerators for Machine Learn-
ing and Robotics. In ECML/PKDD-2014 PhD Session
Proceedings, Nancy.
Yi, Y., Wu, J., and Xu, W. (2011). Incremental SVM based
on reserved set for network intrusion detection. Expert
Systems with Applications, 38(6):7698–7707.
Zander, T. O. and Kothe, C. (2011). Towards passive brain-
computer interfaces: applying brain-computer inter-
face technology to human-machine systems in gen-
eral. Journal of Neural Engineering, 8(2):025005.
Comparison of Data Selection Strategies for Online Support Vector Machine Classification
67
