Measuring Temporal Parameters of Gait with Foot Mounted IMUs in

Steady State Running

G. P. Bailey and R. K. Harle

Computer Laboratory, University of Cambridge, William Gates Building, 15 JJ Thomson Avenue, Cambridge, U.K.

Keywords:

Running, Gait, Temporal Gait Parameters, Foot Kinematics, Continuous Sensing, Toe-off, Heel-strike,

Cadence, Contact-time.

Abstract:

The continuous sensing of running biomechanics provides an opportunity to monitor changes in sporting tech-

nique for performance or injury prevention. Inertial sensors are now small enough to integrate into footwear,

providing a potential platform for continuous monitoring that does not require additional components to be

worn by the athlete and that can be used to assess foot kinematics during running as well as temporal parame-

ters. While temporal parameters of gait are already widely used, they may be combined with the measurement

of foot kinematics assessed using a wearable — Inertial Measurement Unit (IMU) based — foot mounted Iner-

tial Navigation System (INS). Assessment of foot pose at times of foot-ground interaction (such as heel-strike

and toe-off) is likely to require excellent accuracy in the face of changing technique and speed. We present and

evaluate a threshold free algorithm for assessing temporal gait parameters using a foot mounted IMU. We also

investigate the impact of errors in temporal gait parameters on the measurement of foot kinematics at these

time points. We ﬁnd that our algorithm has good accuracy, for example we ﬁnd a mean error 0.47 ± 3.84ms

for toe-off estimation at a running velocity of 3.4ms

−1

. We also ﬁnd that the magnitude of this error has

little affect on some spatial parameter measurements, such as frontal plane foot angle (at a running speed

of 2.3ms

−1

, mean error at toe-off was 0.93 ± 2.07

◦

). However, for others the error in temporal parameters

produces larger changes, for example sagital plane foot angle (at a running speed of 2.3ms

−1

, mean error at

toe-off was 4.11

◦

± 3.70).

1 INTRODUCTION

Biomechanical assessment of movement is a compli-

cated but valuable component of todays elite sports

training. Assessment of running gait is particularly

important and is usually performed within a labo-

ratory setting. These assessments are often charac-

terised by expensive equipment, manual analysis and

subjective metrics. Furthermore the restricted space

of a laboratory necessitates evaluation either using a

small number of steps or, more often, a treadmill. In

neither case is the athlete free to move naturally and

there is little guarantee that the gait exhibited is that

found in the true sporting arena.

In order to address these issues and to bring

such biomechanical assessment to a wider audience,

low-cost inertial sensors are being embedded within

consumer products, allowing athletes to be assessed

in their natural setting and, additionally, more fre-

quently. Such in-ﬁeld constant-assessment brings

with it additional beneﬁts, including tracking the

progress of injury rehabilitation and enabling longi-

tudinal sports science and biomechanical studies

Foot-mounted sensors are popular since

lightweight sensors can be embedded within

shoes in a convenient, unobtrusive way. They may be

able to capture rich data, and have already attracted

commercial interest (e.g. the Nike+ shoe). In the

future, such sensors may be able to track relevant

performance metrics or detect poor or compensatory

patterns of gait.

Temporal parameters of gait are of particular inter-

est when measuring gait. These parameters include

the time of heel-strike and toe-off which in turn can

be used to assess other temporal parameters, such as

ﬂight time, contact time, and cadence, all of which are

of interest to athletic coaches and biomechanists.

Temporal parameters of gait give important in-

formation regarding the gait cycle, for example con-

tact time (derived from the difference in time be-

tween heel-strike and toe-off events) is of use to sprint

coaches, where there is a relationship between contact

time and speed. Contact time has also been identiﬁed

as a useful measure of technique during a survey of

Bailey, G. and Harle, R..

Measuring Temporal Parameters of Gait with Foot Mounted IMUs in Steady State Running.

In Proceedings of the 3rd International Congress on Sport Sciences Research and Technology Support (icSPORTS 2015), pages 24-33

ISBN: 978-989-758-159-5

athlete and coaches perceptions of technology needs

(Fleming et al., 2010) and has been suggested as a

method of assessing running skill level (Strohrmann

et al., 2012). Cadence may also be derived from tem-

poral parameters and is a useful clinical measurement

(Dugan and Bhat, 2005). It has been suggested that

reduction in stride length may reduce the probability

of stress fractures (Edwards et al., 2009), cadence is,

therefore, an important metric for coaches and ath-

letes since the only way to reduce stride length —

without a change in running velocity — is to increase

cadence. Cadence measurement may also be useful

for the coach or athlete trying to optimise cadence for

performance purposes.

Previous work has enabled the trajectory of the

foot to be assessed using foot worn sensors in both

running (Bailey and Harle, 2014) and walking (Mar-

iani et al., 2010). Foot trajectory may become even

more useful when combined with temporal parameter

measurement. The foot trajectory is a rich source of

information and it may be helpful to interpret it with

the help of temporal gait parameters. The foot makes

it’s contribution to locomotion while in contact with

the ﬂoor, this means it is important to know the cir-

cumstances in which the foot ﬁrst made contact with

the ground, and further, the circumstances with which

it terminated contact with the ﬂoor.

Providing both temporal parameters and spatial

parameters of gait from data obtained from a shoe

mounted Inertial Measurement Unit (IMU) is desir-

able and since spatial parameters have been previ-

ously investigated (Bailey and Harle, 2014), assess-

ment of temporal parameters using a foot mounted

IMU is an important next step. The purpose of this

study is to provide an algorithm to estimate tempo-

ral parameters of gait using a foot mounted IMU. The

affects of the accuracy of temporal parameters on the

estimation of spatial parameters at heel-strike and toe-

off will also be investigated.

We address the following research questions:

• Is it possible to use a foot mounted IMU to mea-

sure temporal parameters of running gait?

Previous studies have used thresholds with ac-

celerometer data to assess temporal parameters or

running gait using a foot mounted IMU. While at-

tempting to use these methods to estimate toe-off

we have found them to be inaccurate and unreli-

able in the face of differing pace. Is it possible to

come up with an algorithm that doesn’t use thresh-

olds to assess temporal parameters of gait and how

accurate is it?

• How does the accuracy of heel-strike and toe-off

estimation affect the measurement of spatial pa-

rameters at these time points?

Previous work has used the strapdown inertial

navigation algorithm together with IMUs to re-

cover the trajectory of the foot during each gait

cycle in steady state running. Heel-strike and toe-

off time could be used in combination with the

trajectory of the foot to assess the pose of the foot

at these time points. What affect does the error in

temporal parameter estimation have on the accu-

racy of spatial measurements of gait at points in

time where the foot interacts with the ground.

2 BACKGROUND

Measurement of temporal parameters of gait using

wearable sensors for in situ monitoring has been stud-

ied in the recent past, however many of the studies

available have concentrated on walking gait or inves-

tigate temporal parameters with sensors attached to

areas of the body that are not the foot and — as as

previously stated — we believe that placing sensors

within the shoe is beneﬁcial in terms of ease and fre-

quency of use. While there has been limited assess-

ment of temporal parameters in running using foot

mounted inertial sensors, many other studies have in-

vestigated temporal gait parameters either in walking

or in running using different sensor placements. Fur-

ther, different sensor systems have also been used,

such as pressure sensors. This section will describe

directly related previous work.

A previous work (Strohrmann et al., 2011) in-

vestigated the assessment of normalised foot contact

time using wearable sensors. To do so the time of

heel-strike and toe-off were estimated using a foot

mounted IMU. Placement of the sensor was on the in-

step of the shoe. Toe-off was detected when the accel-

eration magnitude exceeded a threshold of 2g follow-

ing a period where the magnitude of the acceleration

was below a particular threshold subsequent to the

detected foot strike. No formal evaluation was pre-

sented for the accuracy of the recovered toe-off and

foot-strike times, but in our experience this algorithm

is inaccurate and differing running pace produced sig-

niﬁcantly different results.

Shank mounted gyroscopes have also been used

to assess contact times in running and walking (Mc-

Grath et al., 2012) where a gyroscope based algorithm

(Greene et al., 2010) was used to to determine heel-

strike and toe-off times. This was evaluated using

optical motion capture data with two different algo-

rithms (Zeni et al., 2008; Hreljac and Marshall, 2000)

applied, these algorithms present a limitation to this

study as they have been found to be inaccurate in run-

ning (Maiwald et al., 2009). The results showed poor

Measuring Temporal Parameters of Gait with Foot Mounted IMUs in Steady State Running

to moderate agreement for stance and swing times but

performed better for stride times.

While not based on inertial sensors, a number of

studies have used pressure sensors embedded within

shoes to assess temporal gait parameters. For exam-

ple, pressure sensors embedded within sprinters shoes

have been used to provide contact times (Harle et al.,

2011). While the system achieved results with a sim-

ilar accuracy to force plate data, pressure sensors can

be prone to break due to the wiring required and the

forces placed upon those wires (and to the sensors

themselves) during vigorous motion. For that reason,

we have chosen to target the use of IMUs instead of

pressure sensors due to the aims of enabling in situ

monitoring, potentially over a long period of time.

By using an IMU based approach we avoid overcom-

ing the problems with reliability of pressure sensors

and make the system viable for lay users and poten-

tial manufacturers alike.

2.1 Current Methods of Assessing

Temporal Parameters

Current methods of assessing temporal parameters are

commonly lab based. The ‘gold standard’ method

of temporal parameter assessment is the use of force

plates. Force plates provide a force/time series, in or-

der to derive temporal parameters a threshold is ap-

plied to the vertical component of the measured force

— this is called the Ground Reaction Force (GRF)

— to detect the increase in force applied to the plate

that corresponds to the contact phase of gait. This

threshold is typically set so that it is large enough

to be above the noise ﬂoor of the sensor and small

enough that there is minimal error in the timing, in

particular 10N is the typical threshold value (Hreljac

and Marshall, 2000; O’Connor et al., 2007; Maiwald

et al., 2009). The use of force plates for temporal gait

analysis methods has limitations however, and these

depend on how the force-plate is used. There are two

different scenarios in which the force plate is used,

the ﬁrst is embedded into the ﬂoor of the laboratory

or running track and the second is embedded within a

treadmill.

When embedded into the ﬂoor or a running track

the area covered by a single force plate is limited to a

small area, typically only big enough to assess a sin-

gle step at a time. This means that the subject be-

ing assessed may modify their gait to hit the plate —

through adaptations of step length (Abendroth-Smith,

1996) and by extension either contact time or cadence

— or miss the area altogether. This means that col-

lecting data on a large number of steps is a laborious

task as many trials have to be discarded if the subject

modiﬁes their gait or misses the plate and the discard-

ing of steps is subject to human judgement and may

be prone to error or bias. Furthermore, there may be

some instances where the sequence of steps leading

up to a particular manoeuvre, such as cutting, is of

importance. This can be very difﬁcult to assess with

force plates and so video may be used introducing a

laborious and subjective digitisation task. Multiple

force plates may be embedded in the track/running

surface but the subject being assessed may not hit

each one, and the extra instrumentation is a large and

unwanted additional cost.

These limitations can to some extent be mitigated

by using a treadmill with an embedded force plate,

this is the other typical usage scenario. However, this

introduces new compromises. Firstly, gait exhibited

on a treadmill may be different to that of walking

or running over ground, particularly if the subject is

unfamiliar with using a treadmill. Secondly, the me-

chanical nature of the treadmill introduces noise to

the force-plate data meaning that the threshold used to

ﬁnd contact times must be increased accordingly, pre-

vious studies have used a threshold of 20N (for exam-

ple (Zeni et al., 2008)). This affects accuracy and con-

sistency with studies based on overground running,

the higher threshold may lead to later estimates of

heel-strike and earlier estimates of toe-off when com-

pared to overground force-plate data. Also, more am-

bitious studies looking at at a series of contact times

prior to a manoeuvre (such as cutting) are impossible

on a treadmill. Finally, they are expensive and rela-

tively uncommon.

The limitations of the above two scenarios suggest

a need to be able to assess temporal parameters in-situ

but with the ability to assess each step in sequence.

3 SENSOR PLATFORM AND

DATA CAPTURE

3.1 Inertial Sensors

Capture of inertial sensor data was facilitated using

the ION (Imperceptible On-body Node) sensor plat-

form (Harle et al., 2011) with the addition of an

IMU providing a three-axis ±16g accelerometer and

±2000

◦

−1

gyroscope (MPU-6000, InvenSense Inc.)

and containing an internal 16 bit Analog-Digital Con-

verter (ADC). The sensor platform is lightweight,

weighing approximately 15 grams in total, including

battery.

All IMU signals were sampled at 1kHz and logged

to on-board ﬂash memory. In all experiments the ION

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

sensor was placed on the lateral side of the shoe in

line with the ankle, as seen in Figure 1. The sensor

was ﬁrmly taped to the outside of the shoe to simu-

late the scenario where it was built into the shoe, per-

haps embedded in the sole in a similar manner to the

Nike+ shoe. Since the algorithm presented in this pa-

per is intended for use along side an Inertial Naviga-

tion System (INS) the placement on the side of the

ankle is informed from an investigation into the valid-

ity of the zero-velocity assumption (Foxlin, 2005). It

has been shown that the sensor position we have used

is among the best suited to using this assumption dur-

ing a study of foot mounted inertial navigation tech-

niques, including an investigation of different mount-

ing locations on the foot (Peruzzi et al., 2011).

3.2 Ground Truth

Ground truth is important for assessing the ability

of any system to assess temporal parameters of gait.

However, the gold standard ground truth of a force

plate was unavailable due to a lack of equipment. Ac-

cess to an optical motion capture system (Vicon) was

available however. Previous studies have attempted to

validate algorithms based on kinematic data from mo-

tion capture to facilitate temporal parameter estima-

tion, these studies have typically focused on walking

gait. In order to validate kinematic data based tempo-

ral parameter estimation in running a previous study

(Maiwald et al., 2009) selected several potential al-

gorithms to evaluate in a running context including

their own ‘Foot Contact Algorithm’ (FCA). The eval-

uation of kinematic data based algorithms for tempo-

ral parameters proceeded with comparison to ground

reaction force data. They found that previously used

algorithms had problems with accuracy but their FCA

algorithm was reported to be accurate in both mea-

surement of heel-strike and toe-off with a similar ac-

curacy and precision to the ground reaction force de-

rived measurement. Therefore, we implemented this

algorithm to use as ground truth for evaluating our

IMU algorithm.

Kinematic data was captured using an optical mo-

tion capture system (Vicon Motion Systems, UK)

sampling at 240Hz. A treadmill was used in order to

capture many steps in a limited motion capture area.

The treadmill was set up without any inclination as

measured with a spirit level. The ION sensor was

attached to a custom jig containing 3 retro-reﬂective

markers (Fig. 1) for the motion capture system, this

setup was previously used to evaluate trajectory re-

covery using a foot-mounted IMU (Bailey and Harle,

2014). The jig in this instance facilitates estimation

of the pose of the foot, and the data is used in order to

assess the affect of errors in temporal parameters on

the estimation of associated spatial parameters. We

use the motion capture data when measuring the af-

fect of temporal parameter error on spatial parameter

determination to isolate the error cause by the tempo-

ral parameters from the potential errors incurred using

an INS solution.

The jig adds an additional 30 grams of weight to

the system (45 grams total, including ION) but re-

mains comfortable for test runs. The jig was laser cut

and the MPU-6000 and retro-reﬂective markers were

aligned with laser-etched outlines to ensure alignment

between the jig and the inertial sensor axes. An addi-

tional marker was placed on the toe to facilitate using

the FCA algorithm. The posterior marker on the jig

was used as the heel marker for the FCA algorithm.

Figure 1: Shoe with IMU and Jig for facilitating ground

truth capture using the Vicon Motion capture system.

3.3 Data Collection

In order to evaluate the temporal parameter estima-

tion algorithm presented in this paper data were col-

lected from 5 participants. Each participant ran for

90 seconds at 4 different speeds. After detection of

the running period, 90 steps were extracted for each

participant at each speed to ensure the same number

of steps were used for each participant. After select-

ing these 90 steps the heel-strike and toe-off detection

was performed for each step. This produced a total of

1800 steps for analysis.

4 TEMPORAL PARAMETER

ALGORITHM

The algorithm proposed in this section takes a divide

and conquer approach to ﬁnding temporal parameters.

Data ﬁles are ﬁrst segmented to ﬁnd periods of run-

ning (run detection), followed by identifying regions

that contain a single step from heel-strike to toe-off

(step segmentation). Once regions containing heel-

strike and toe-off events from a single step are iden-

tiﬁed, consistent features of the step are used to seg-

ment the signal further to get more accurate temporal

parameter estimations.

Measuring Temporal Parameters of Gait with Foot Mounted IMUs in Steady State Running

4.1 Running Detection and Step

Segmentation

This section will describe the process of run detection

and step segmentation before returning to the tempo-

ral parameter estimation later.

4.1.1 Normalised Auto-correlation based Step

Counting

A modiﬁed version of the Normalised Auto-

correlation based Step Counting algorithm (NASC

(Rai et al., 2012)) is used to ﬁrst detect periods of

running and then to roughly segment the signal into

individual steps for further inspection to ﬁnd tempo-

ral parameters.

The NASC algorithm exploits the periodicity of

gait in order to detect periods of walking. The al-

gorithm uses auto-correlation of an inertial signal.

Given that inertial signals measured during gait are

periodic the auto-correlation value should be at it’s

largest at the correct periodicity of the gait cycle. The

NASC algorithm was developed to work with inertial

sensors placed in any location on the body to detect

walking via detecting periodic motion. In this case,

the location of the sensor is known and the mode of

gait is running rather than walking. This means that

the algorithm is modiﬁed accordingly to take advan-

tage of this knowledge.

The original algorithm uses the acceleration sig-

nal for walk detection. For this work, sagital plane

angular rate (g

) is used since there is lower noise and

higher step to step repeatability with this signal for

our particular application using a foot-mounted IMU.

This can be seen in Figure 2.

0 500 1000 1500 2000 2500 3000

Time (ms)

−15

−10

−5

ion

(rad/s)

Figure 2: Example showing ﬁve steps of sagital plane angu-

lar rate (g

ion

Given a signal — in this case g

ion

(n) — the NASC

algorithm computes the normalised auto-correlation χ

for lag τ at the m

sample as described by the follow-

ing two equations that have been split for readability.

χ(m, τ) =

∑

k=τ−1

k=0

[α(m,τ,k)α(m+τ,τ,k)]

τσ(m,τ)σ(m+τ,τ)

(1)

α(i, τ, k) = g

ion

(i + k) − µ(i, τ) (2)

In Equations 1 and 2, µ(k, τ) and σ(k, τ) are the

mean and standard deviation of the sequence of sam-

ples < g

ion

(k), g

ion

(k + 1), ..., g

ion

(k + τ − 1) >.

When the subject wearing the sensor is running

(or walking) and τ is exactly equal to the period of the

acceleration pattern, the normalised auto-correlation

will be close to one. However, τ is unknown and

so NASC tries values of τ between selected values of

min

and τ

max

to ﬁnd the value of τ for which χ(m, τ)

becomes maximum (τ

opt

). This is described by the

following equation.

ψ(m) = max

τ=τ

max

τ=τ

min

(χ(m, τ)) (3)

The implementation presented in (Rai et al., 2012)

used a search window (τ

min

,τ

max

) of (0.8s,2s) for

walking, this is based on the typical two step duration

of walking. However our scenario is treadmill run-

ning and so a search window of (0.6s, 0.9s) is used

based on the cadence of the runners tested during the

experiments in this paper.

The maximum normalised auto-correlation, ψ(m),

simultaneously provides two pieces of information

(Rai et al., 2012). Firstly, a high value (close to 1)

suggests that the person is running or walking since

it implies a high level of repeatability in the signal

in typical gait cadence ranges, this can be used for

run (or walk) detection,. Secondly, the corresponding

value of τ = τ

opt

gives the periodicity of the persons

gait. A moving average ﬁlter with a 5 second window

is used for both ψ(m) and τ

opt

signals and an example

of the resulting signals is given in Figure 3.

0 20000 40000 60000 80000 100000 120000

100

200

300

400

500

600

700

800

900

opt

(ms)

opt

0.0

0.2

0.4

0.6

0.8

1.0

ψ(m)

Figure 3: Graph showing τ

opt

and ψ(m) with 5s moving

average ﬁlter applied. Shaded area shows the period of de-

tected running.

4.1.2 Run Detection

Periods of running are detected in a similar manner

to (Rai et al., 2012). However, since the experi-

ments here are constrained to small data ﬁles where

we know that running forms the majority of the ﬁle, a

simpler algorithm is used that doesn’t take account of

previous states and only uses a threshold on the value

of ψ(m). A threshold value of 0.8 is used, any value

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

of ψ(m) above 0.8 is deemed to be a period of running

(Figure 3). This detection method would likely need

to take into account previous states as in (Rai et al.,

2012) were the ﬁle to consist of more free form mo-

tion with periods of running interspersed with other

activities. This was outside of the scope of the current

work.

4.1.3 Single Step Segmentation

The NASC algorithm was originally designed for step

counting (Rai et al., 2012), however, we are interested

in segmenting the steps rather than counting them and

therefore the algorithm was modiﬁed for this work in

order to segment steps. An additional requirement is

that it needs be robust to changes in speed and there-

fore should not rely on thresholds.

Setting thresholds is not desirable as they are not

robust to changes in running technique, running ve-

locity and other factors that affect the magnitude of

the peaks of the inertial measurements. This makes

robust algorithms that yield few false positives hard

to code. This also removes the need for constraints —

such as detection of improbable cadences — that are

required in order to detect missed peaks due to them

being lower than the threshold used.

The NASC algorithm not only enables robust de-

tection of running steps, but the value of t

opt

(m) gives

an estimate of the time between heel-strike events,

this could otherwise be described as the gait period

(or the inverse of cadence). This information can be

used in order to segment steps based on some repeat-

able and easily detectable signal feature.

The segmentation proceeds by ﬁrst looking for

one of the clear peaks in the g

ion

signal near to t

start

the start time of the detected period of running. In

order to avoid thresholds we look for the maximum

value of g

ion

in the ﬁrst two seconds.

ts(1) = time(max

t=t

start

+2τ

opt

start

))

t=t

start

ion

(t))) (4)

Here, ts(1) is the time of the ﬁrst step segment.

This may end up missing a single step at the start,

this is due to the size of the initial search window.

This window contains approximately two steps worth

of data either of which could contain the maximum

value so the ﬁrst is not necessarily selected. This gives

a clear and simple to implement method of gaining a

single peak to identify as a start point for further seg-

mentation. The peak detected represents the start of

the ﬁrst step segment. The time of subsequent seg-

ments are found using in a similar manner by looking

in a window deﬁned by the periodicity of the run at

the last peak τ

opt

(ts(n)), where n is the segment num-

ber.

ts(n + 1) = time(max

t=ts(n)+

6τ

opt

(ts(n))

t=ts(n)+

opt

(ts(n))

ion

(t))) (5)

This results in rough segmentation from which the

temporal parameters can be further reﬁned. Figure

4 shows an example of the results of segmentation.

Each segment (ts(n), ts(n + 1)) is guaranteed to con-

tain a heel-strike and toe-off event, this is because the

maximum sagital plane angular rate of the foot is dur-

ing the ﬂight phase of gait. This makes identifying

these events a much simpler task that attempting to

identify correctly all heel-strike events given a period

of data containing multiple steps.

0 500 1000 1500 2000 2500 3000 3500 4000

Time (ms)

−15

−10

−5

ion

(rad/s)

Figure 4: Segmentation of g

ion

using NASC algorithm to

ﬁnd successive peaks, vertical lines show start times of suc-

cessive segments (ts(n)).

4.2 Finding Heel-strike and Toe-off

Points

Now that the running ﬁle has been segmented into

sections each containing a single heel-strike and toe-

off event, the algorithm further splits the step into

easy to ﬁnd pieces before attempting to ﬁnd the more

subtle features associated with heel-strike and toe-off

events. The process for each event will be described

in the following sections.

4.2.1 Heel-strike

Heel-strike is found by looking for the large changes

in signal associated with heel-strike. We again use the

ion

signal for this task due to it having relatively little

noise compared with the accelerometer signal.

Large changes in a signal can be more easily de-

tected by assessing the ﬁrst differential. Heel-strike

is assessed by inspecting the signal in a region de-

ﬁned using the course segmentation deﬁned in Sec-

tion 4.1.3, sagital plane angular rate for a subset of

a region (ts(n), ts(n + 1)) is shown in Figure 5. For

each coarse segment, the differential of the g

ion

signal

is calculated. Then the minimum value of the result-

ing signal is found, this is shown as the marked circle

in Figure 5 and deﬁned in Equation 6.

(n) = time(min

t=ts(n)

t=ts(n+1)

0ion

(t))) (6)

Here t

(n) is the ﬁrst estimate of the time of heel

strike for step n, ts(n) is the time of the start of a

Measuring Temporal Parameters of Gait with Foot Mounted IMUs in Steady State Running

200 220 240 260 280 300 320

−20

−15

−10

−5

ion

(rad/s)

ion

−5

−4

−3

−2

−1

ion

(rad/s

)

ion

Figure 5: Heel-strike detection from sagital plane angular

rate.

coarse segment for step n and g0

ion

(t) is the differen-

tial of the g

ion

(t) signal. This detects a rough estimate

for the time of heel-strike which is then reﬁned in the

following way.

The peak in the differential represents the max-

imum rate of change, but this is logically after the

heel-strike due to the deformity of the mid-sole of the

shoe on impact meaning that the true time of heel-

strike should be at the base of this peak. Therefore

this estimate is reﬁned by seeking backwards in time

to ﬁnd the base of the local minima. Therefore the al-

gorithm seeks backwards from t

(n) up to the point

where g0

ion

(t) is greater than -0.5, this point is then

taken to be the detected heel-strike event t

(n). The

detected time of heel-strike is shown as the vertical

dashed line in Figure 5.

4.2.2 Toe-off

While heel-strike has associated large peaks in in-

ertial data that are easy to detect, the way the foot

peels away from the ﬂoor before toe-off means that

large signal changes don’t exist at toe-off using a heel

mounted IMU. The best algorithm found by us for

toe-off with a heel-mounted sensor depends on ﬁnd-

ing a small local maxima, in the a

ion

(t) signal. The

ion

(t) channel is aligned with the shank during static

standing. As this local maxima is relatively small it

is hard to ﬁnd a reliable algorithm to detect it without

further segmentation of the step. Further segmenta-

tion of the step allows easier detection of the relevant

local maxima.

The segmentation is done by ﬁnding the zero

crossing in the g

ion

(t) signal as shown by the verti-

cal lines in Figure 6a. Once the zero crossings are

found we look in a window deﬁned using the follow-

ing formulae.

start

= c

+ c

)

(7)

end

4(c

− w

start

)

+ w

start

(8)

Here, w

start

and w

end

are the times of the start

and end of the window respectively and c

and c

are

the ﬁrst and second zero crossings. This window is

marked by the vertical lines in Figure 6b. This nar-

rows down the signal enough that we can now re-

liably ﬁnd the minima in the a

ion

(t) signal between

start

and w

end

, this point corresponds to toe-off (Fig-

ure 6b).

0 100 200 300 400 500 600

Time (ms)

−20

−15

−10

−5

(rad/s)

(a) Further segmentation using zero crossings is demonstrated

by the vertical lines.

0 100 200 300 400 500 600

Time (ms)

−50

(ms

−2

)

(b) Toe-off detection. Solid vertical lines show w

start

and w

end

dashed vertical line shows detected toe-off.

Figure 6: Further segmentation in order to ﬁnd toe-off.

This point is less well deﬁned at slower speeds how-

ever and may impact upon the accuracy at slower

speeds, this is shown in the results of the evaluation.

4.3 Applicability

We have chosen the above algorithm after trying

many other potential algorithms. This algorithm has

the disadvantage that it is most likely dependant on

sensor position, particularly alignment, however the

alignment chosen for the the sensor and shoe should

be easy to replicate with the sensor built into the shoe

as it is positioned roughly perpendicular to the sur-

faces of the mid-sole. It should also be possible to

make small changes to the algorithm for differing

alignment such as swapped axes directions meaning

ﬁnding minimum points need to be substituted for

maximum points, for example. This should mean the

algorithm remains applicable to a sensor system built

into the shoe, but may not be sufﬁciently general for

an inertial system attached, for example, to the laces

of a standard shoe.

4.4 Evaluation

The errors in heel-strike and toe-off estimation us-

ing the inertial sensor based algorithm in this section

are presented in Table 1. The results show mixed ac-

curacy between different running speeds and are de-

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

pendant on the temporal parameter being assessed.

At lower speeds there is slightly lower accuracy and

higher variability in the toe-off metric, this is due to

the peak in a

ion

used to assess toe-off being wider and

not as sharp leading to less precise estimates at lower

speeds. The heel-strike assessment is not subject to

this problem due to the relatively large peaks associ-

ated with heel-strike.

Table 1: Mean and Standard Deviation of Errors estimating

temporal parameters in comparison to those derived from

the FCA algorithm. TO = Toe-Off, HS = Heel-Strike.

Speed Error TO (ms) Error HS (ms)

2.3ms

−1

12.63 ± 9.90 9.86 ± 6.99

2.7ms

−1

6.95 ± 7.74 9.91 ± 4.61

3.0ms

−1

2.48 ± 5.99 9.82 ± 3.98

3.4ms

−1

0.47 ± 3.84 9.89 ± 3.37

Contact times were derived from the results of

the inertial algorithm for comparison with previous

methods demonstrated earlier in this chapter. A small

bias of -4.37ms was found with limits of agreement

-23.50ms to 14.76ms. A Bland-Altman plot can be

seen in Figure 7. Cadence was also calculated and a

Bland-Altman plot of the results can be seen in Fig-

ure 8, there is a small bias of 0.002 steps per minute

and limits of agreement of 2.45 to -2.49 steps per

minute, however the ﬁgure demonstrates that occa-

sionally there are signiﬁcant outliers.

200 220 240 260 280 300 320 340 360 380

Mean Contact Time (ms)

−60

−40

−20

Contact Time Difference (ms)

Figure 7: Bland-Altman plot of contact times derived from

a heel mounted IMU.

130 140 150 160 170 180 190

Mean Cadence (steps per minute)

−10

−5

Cadence difference (steps per minute)

Figure 8: Bland-Altman plot of cadence derived from a heel

mounted IMU.

5 AFFECT OF TEMPORAL

PARAMETER ESTIMATION

ERRORS ON SPATIAL

PARAMETER MEASUREMENT

An algorithm for determining heel-strike and toe-off

times using a heel mounted IMU has been presented

and evaluated. One of the reasons for developing such

an algorithm is to be able to evaluate spatial parame-

ters of gait using foot mounted INS methods (Bailey

and Harle, 2014). The temporal parameter estimation

described in the previous section is not perfect and has

some associated error. This section investigates how

that error affects the estimation of spatial parameters

of gait at heel-strike and toe-off events.

5.1 Evaluation Method

The FCA algorithm provided heel-strike and toe-off

times and the jig data were used to derive the angle

of the foot at these time points. The angle of the foot

is used as a potentially interesting spatial parameter

that might be evaluated at toe-off and heel-strike but

any other metric could potentially be calculated. At

heel-strike the angles of the foot in the sagital plane

(θ

(t)) and frontal plane θ

(t) were evaluated for each

step i from the Vicon data. These angles were also

evaluated at toe-off.

Further, the angle of the foot was recorded for

each step at multiple time points, calculated as offsets

from the output of the FCA algorithm. For example,

for step i, θ

(t) would be calculated for a sequence

of times t =< t

(i)− 20, t

(i)− 10, t

(i)+ 0, t

(i)+

10,t

(i) + 20 > (times measured in milliseconds).

This series of measurements are designed to show the

progression of foot angle (an example of a spatial pa-

rameter) in the time period around the temporal event

of interest in order to assess accuracy requirements

for temporal parameters. Finally, foot orientation dif-

ferences are measured between time points measured

using the output of the ION based temporal parameter

estimation and FCA measured time points.

5.2 Results

The angles calculated from the Vicon data at various

time points are then turned into deltas from the angle

at t = t

(i), for example θ

(i) − 20) − θ

(i)).

The results are shown in Table 2. The results show

that the error depends on the measurement being

taken, for example the error in the frontal plane at toe

off is relatively unchanged 20ms prior to and 20ms

after toe-off but the sagital plane angle varies greatly.

Measuring Temporal Parameters of Gait with Foot Mounted IMUs in Steady State Running

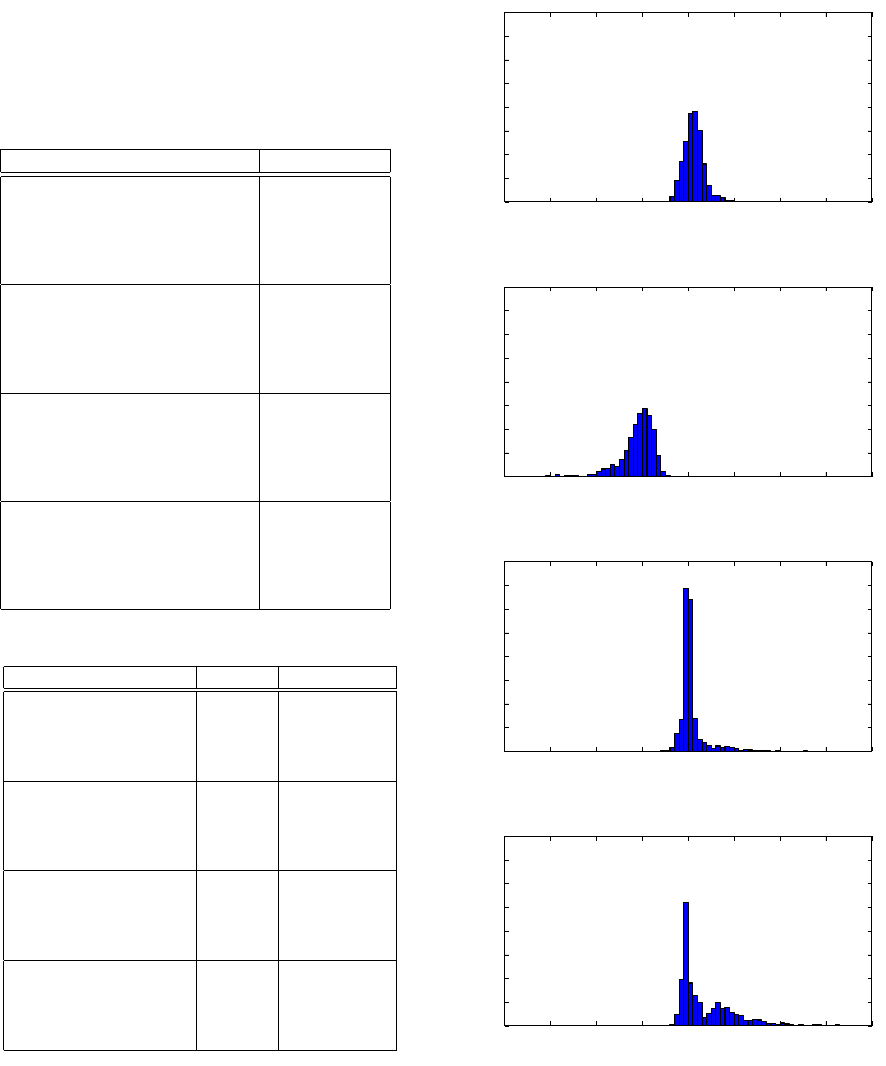
This indicates that the spatial parameter being mea-

sured may greatly affect the measurement accuracy

of temporal parameters required for accurate spatial

parameter measurement.

Table 2: Foot angle error at particular time offsets.

Measurement Error (ms)

f ca

(i) − 20) − θ

f ca

(i)) 0.87 ± 1.43

f ca

(i) − 10) − θ

f ca

(i)) 0.58 ± 1.07

f ca

(i) + 10) − θ

f ca

(i)) 2.96 ± 2.15

f ca

(i) + 20) − θ

f ca

(i)) 5.11 ± 2.95

f ca

(i) − 20) − θ

f ca

(i)) −6.25 ± 1.91

f ca

(i) − 10) − θ

f ca

(i)) −5.40 ± 1.38

f ca

(i) + 10) − θ

f ca

(i)) 6.77 ± 1.36

f ca

(i) + 20) − θ

f ca

(i)) 12.28 ± 2.22

f ca

(i) − 20) − θ

f ca

(i)) 1.72 ± 1.67

f ca

(i) − 10) − θ

f ca

(i)) 0.48 ± 1.06

f ca

(i) + 10) − θ

f ca

(i)) 0.02 ± 1.37

f ca

(i) + 20) − θ

f ca

(i)) 0.23 ± 2.93

f ca

(i) − 20) − θ

f ca

(i))

7.81 ± 1.77

f ca

(i) − 10) − θ

f ca

(i)) 3.72 ± 0.92

f ca

(i) + 10) − θ

f ca

(i)) −2.78 ± 0.71

f ca

(i) + 20) − θ

f ca

(i)) −5.04 ± 1.38

Table 3: Foot angle error between FCA and ION.

Measurement Speed Error (ms)

ion

(i)) − θ

f ca

(i)) 2.3ms

−1

−4.56 ± 2.02

2.7ms

−1

−5.18 ± 1.68

3.0ms

−1

−5.79 ± 1.60

3.4ms

−1

−6.60 ± 2.04

ion

(i)) − θ

f ca

(i)) 2.3ms

−1

0.33 ± 1.25

2.7ms

−1

0.46 ± 1.16

3.0ms

−1

0.71 ± 1.25

3.4ms

−1

0.71 ± 1.18

ion

(i)) − θ

f ca

(i)) 2.3ms

−1

4.11 ± 3.70

2.7ms

−1

2.51 ± 2.82

3.0ms

−1

1.06 ± 2.51

3.4ms

−1

0.22 ± 1.64

ion

(i)) − θ

f ca

(i)) 2.3ms

−1

0.93 ± 2.07

2.7ms

−1

0.08 ± 1.12

3.0ms

−1

0.14 ± 0.97

3.4ms

−1

0.14 ± 0.52

Figure 9 shows the distribution of errors for foot

angles at both toe-off and heel-strike and includes re-

sults for all speeds. Errors at heel-strike show similar

results to those at toe-off with the sagital plane be-

ing most affected. The mean error in frontal plane

angle at heel-strike between heel-strike measured by

FCA vs. ION was 0.56 ± 1.22 degrees. By contrast

the mean sagital plane error was −5.56 ± 2.01 de-

−20 −15 −10 −5 0 5 10 15 20

∆Angle(Degrees)

100

200

300

400

500

600

700

800

Frequency

(a) θ

ion

(i)) − θ

f ca

(i)).

−20 −15 −10 −5 0 5 10 15 20

∆Angle(Degrees)

100

200

300

400

500

600

700

800

Frequency

(b) θ

ion

(i)) − θ

f ca

(i)).

−20 −15 −10 −5 0 5 10 15 20

∆Angle(Degrees)

100

200

300

400

500

600

700

800

Frequency

ion

(i)) − θ

f ca

(i)).

−20 −15 −10 −5 0 5 10 15 20

∆Angle(Degrees)

100

200

300

400

500

600

700

800

Frequency

(d) θ

ion

(i)) − θ

f ca

(i)).

Figure 9: Difference in foot angle at temporal events mea-

sured by the ION and FCA algorithms.

grees. Again, this shows the magnitude of errors in

spatial parameters that are affected by a difference in

measured temporal parameters from reality is depen-

dant on the spatial parameter being measured. Re-

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

sults may also be dependant on individual technique,

Figure 9d shows a small secondary peak at 4 degrees

while the main peak is centred on 0 degrees. This may

mean that measurement error depends on an individ-

ual athletes technique as well as the measurement be-

ing evaluated.

Table 3 shows the angular errors obtained for the

time difference between the ION temporal parameters

algorithm and the FCA algorithm, broken down by

speed. The table shows that the slowest speeds have

the largest error for foot angle in the sagital plane but

the frontal plane is again relatively unaffected.

6 CONCLUSIONS

A method of reliably ﬁnding temporal parameters of

gait from a foot mounted IMU has been presented and

evaluated. The method presented is free of thresh-

olds that may be unreliable in the face of changing

technique and running pace. However, it is likely that

the algorithm will only work with the sensor position

used within this paper. The algorithm was designed

with a view to the sensors being built into the mid-sole

of the shoe so we view this as a minor limitation. The

algorithm has usable accuracy for temporal parameter

estimation but its accuracy for toe-off is somewhat de-

pendant on running velocity. The impact of the mag-

nitude of this error on the estimation of spatial metrics

was also investigated and shows that some metrics are

likely to be more affected than others. We ﬁnd that

for some metrics there are minimal errors in spatial

parameters measured at time points derived from the

foot IMU data. Further work should seek to evaluate

the temporal parameter algorithm to check for accu-

racy and robustness in outdoor over ground running

to enable practical training and biomechanical assess-

ment tools.

REFERENCES

Abendroth-Smith, J. (1996). Stride Adjustments during a

Running Approach toward a Force Plate. Research

Quarterly for Exercise and Sport, 67(1):97–101.

Bailey, G. and Harle, R. (2014). Assessment of Foot Kine-

matics During Steady State Running Using a Foot-

mounted IMU. Procedia Engineering, 72:32–37.

Dugan, S. A. and Bhat, K. P. (2005). Biomechanics and

analysis of running gait.

Edwards, W. B., Taylor, D., Rudolphi, T. J., Gillette, J. C.,

and Derrick, T. R. (2009). Effects of stride length

and running mileage on a probabilistic stress fracture

model. Medicine and Science in Sports and Exercise,

41:2177–2184.

Fleming, P., Young, C., Dixon, S., and Carr

e, M. (2010).

Athlete and coach perceptions of technology needs for

evaluating running performance. Sports Engineering,

13(1):1–18.

Foxlin, E. (2005). Pedestrian tracking with shoe-mounted

inertial sensors. IEEE Computer Graphics and Appli-

cations, 25(6):38–46.

Greene, B. R., McGrath, D., O’Neill, R., O’Donovan, K. J.,

Burns, A., and Caulﬁeld, B. (2010). An adaptive

gyroscope-based algorithm for temporal gait analysis.

Medical and Biological Engineering and Computing,

48:1251–1260.

Harle, R., Taherian, S., Pias, M., Coulouris, G., Hopper, A.,

Cameron, J., Lasenby, J., Kuntze, G., Bezodis, I., Ir-

win, G., and Kerwin, D. G. (2011). Towards real-time

proﬁling of sprints using wearable pressure sensors.

Computer Communications.

Hreljac, A. and Marshall, R. N. (2000). Algorithms to deter-

mine event timing during normal walking using kine-

matic data. Journal of Biomechanics, 33:783–786.

Maiwald, C., Sterzing, T., Mayer, T., and Milani, T. (2009).

Detecting foot-to-ground contact from kinematic data

in running. Footwear Science, 1(2):111–118.

Mariani, B., Hoskovec, C., Rochat, S., B

ula, C., Penders, J.,

and Aminian, K. (2010). 3D gait assessment in young

and elderly subjects using foot-worn inertial sensors.

Journal of Biomechanics, 43:2999–3006.

McGrath, D., Greene, B. R., ODonovan, K. J., and

Caulﬁeld, B. (2012). Gyroscope-based assessment of

temporal gait parameters during treadmill walking and

running. Sports Engineering, 15(4):207–213.

O’Connor, C. M., Thorpe, S. K., O’Malley, M. J., and

Vaughan, C. L. (2007). Automatic detection of

gait events using kinematic data. Gait and Posture,

25:469–474.

Peruzzi, A., Della Croce, U., and Cereatti, A. (2011). Es-

timation of stride length in level walking using an in-

ertial measurement unit attached to the foot: A vali-

dation of the zero velocity assumption during stance.

Journal of Biomechanics, 44:1991–1994.

Rai, A., Chintalapudi, K. K., Padmanabhan, V. N., and Sen,

R. (2012). Zee: Zero-Effort Crowdsourcing for Indoor

Localization. In Proceedings of the 18th annual in-

ternational conference on Mobile computing and net-

working - Mobicom ’12, page 293.

Strohrmann, C., Harms, H., Tr

oster, G., Hensler, S., and

uller, R. (2011). Out of the lab and into the woods:

kinematic analysis in running using wearable sensors.

In Proceedings of the 13th international conference on

Ubiquitous computing, pages 119–122. ACM.

Strohrmann, C., Rossi, M., Arnrich, B., and Troster, G.

(2012). A Data-Driven Approach to Kinematic Anal-

ysis in Running Using Wearable Technology. 2012

Ninth International Conference on Wearable and Im-

plantable Body Sensor Networks, pages 118–123.

Zeni, J. A., Richards, J. G., and Higginson, J. S. (2008).

Two simple methods for determining gait events dur-

ing treadmill and overground walking using kinematic

data. Gait and Posture, 27:710–714.

Measuring Temporal Parameters of Gait with Foot Mounted IMUs in Steady State Running