A Case Study of Para Table Tennis Athlete’s Functional Ability

Davy Lim

, Yap Wen Bin

, Zachary Tan

, Holden Li

and Phillis Teng

Institute for Sports Research, Nanyang Technological University, Singapore, Singapore

School of Mechanical and Aeronautical Engineering, Nanyang Technological University, Singapore, Singapore

Keywords: Para Athletes, Table Tennis and Functional Reach.

Abstract: Reach is an important performance aspect for para table tennis athletes under the seated classifications of 1

and 2. The aim of this pilot study was to define the effective reach of Class 1 and 2 para table tennis

athletes. Three players, 3 from Class 1 and 2 took part in this investigation. During the static assessment,

players were asked to perform full reach from a seated position across the table tennis table, with the area

outlined as Sweep Area (SA). In the dynamic assessment, players hit a series of balls propped up along the

perimeter of the SA. The average SA for Class 1 and 2 were 0.560±0.08m

and

0.640±0.04m

respectively.

The average Right and Left Tipping Angle (RTA, LTA) on the frontal plane were ±20.7° and ±22.0° for

Class 1, and 49.3° and 36.0° for Class 2. Class 1’s average Sweep Time (ST) was 4.92±0.98s, whereas

Class 2’s average ST was 3.69±0.58s. There is a difference in RTA between Class 1 and 2 players. For

future work more samples are needed to understand the athletes’ Range of Motion (ROM). Findings will

serve as important considerations for training design, game strategy and equipment usage.

1 BACKGROUND

Para table tennis is similar in play to regular table

tennis where the primary objective is to prevent the

opponent from hitting a return ball. Para table tennis

allows athletes with physical limitations play with

their mobility aid like a clutch, prosthesis or wheel

chair. Paralympic Table Tennis, particularly for

Class 1 and 2 players is an area with limited research

within academic literature. Current studies in Sports

science on Para Sports has a strong emphasis on

terrestrial and aquatic locomotive strategy for Para

athletes (Dingley et al., 2014) and (Bernardi et al.,

2013), strategic demands of Para team sports (Hegde

and Standal, 2013) or a generic strength training

requirements for Para-Athletes (Borges¹ et al.,

2014). Studies that attempt to investigate a specific

class of athlete in Para sport are still limited

moreover for Para Table Tennis. For the purpose of

fair play, the International Table Tennis Federation

(ITTF) Classification code (Federation, 2010)

classifies players into categories, dependent on their

available joint and movement range. For the class 1

and 2 category, it covers players with only limited

upper body mobility, usually the arms and shoulders.

The Class 1 and 2 players play the game with

modified movements using push pull movements

from their arms and shoulders against the wheel

chairs to reach for the ball. The return technique is a

limited forehand or backhand using a bat strapped to

their hands. A distinguishing difference between the

class 1 and 2 athletes is the limitation of the upper

body and arm movements. Class 1 players usually

have little or no elbow extension and functional

triceps. Both classification of players have no sitting

balance and requires the non-playing arm to

maintain their balance. The varying levels of upper

body mobility also require the players to develop an

individualised movement strategy on their existing

wheel chair. There are some who anchor their arms

on the wheel chair push handle or to be restrained by

a chest belt. Apart from trying to maximise their

reach, these athletes have to battle the fear of falling

off their chair.

2 OBJECTIVE

The objective of the study is to measure and

characterise the effective reach of class 1 and 2 para

table tennis players. The findings are to be used to

influence training design, play strategy and provide

design inputs for an athlete specific Para Table

Tennis concept chair.

Lim, D., Bin, Y., Tan, Z., Li, H. and Teng, P..

A Case Study of Para Table Tennis Athlete’s Functional Ability.

In Proceedings of the 3rd International Congress on Sport Sciences Research and Technology Support (icSPORTS 2015), pages 169-173

ISBN: 978-989-758-159-5

169

3 METHODS

3.1 Data Capture: Reach Perimeter

Six Para Table Tennis Player from the National

Table Tennis team, three from both Class 1 and 2

classifications volunteered for the study. Given the

nature of the sport, the population size for these 2

classifications are very limited. All the players had

at least 2 years of international competitive

experience in para table tennis. They were seated on

their competition chair with their sternum referenced

to the centre line of the table as it is the most

common seating preparation for Class 1 and 2

(Huang et al., 2010). With shoulders parallel to the

table edge, the most superior position of the

acromion was then used to position the player,

300mm away from the table (Figure 2). This

distance is necessary to accommodate the player’s

chair and arm space. Subsequently each of the

players drew a perimeter that represented their

maximal reach on a piece of paper attached to the

table. The perimeter was drawn with a marker

attached to their hands. The total reachable area on

the table by the player defined as Sweep Area (SA).

This measurement is approximated using the mid-

point Riemann method in 100mm increment from

the identified perimeter on the paper. This

calculated area is normalised in terms of percentage

of the player’s playing area. This percentage is

defined as Percentage of Table (POT).

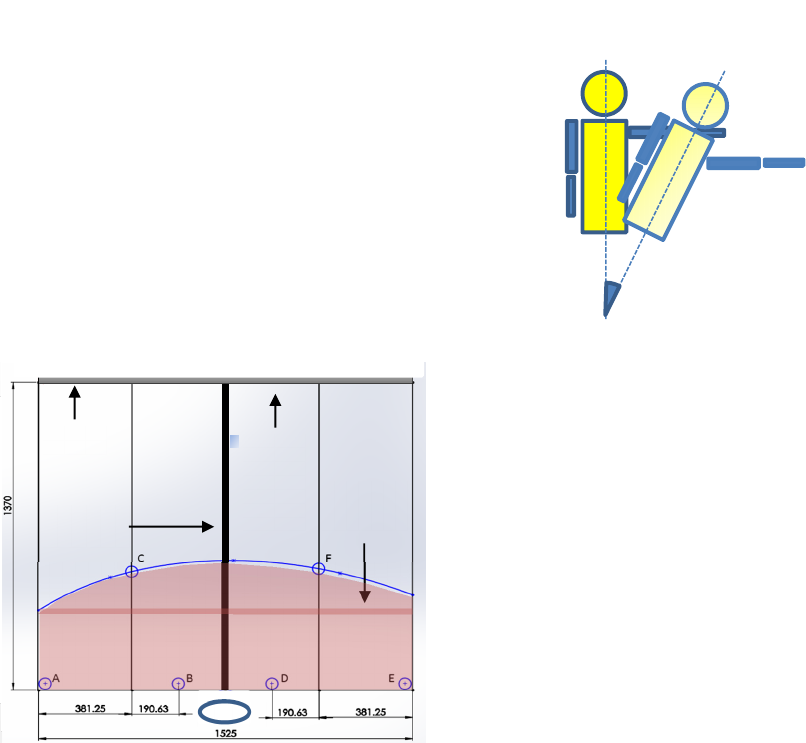
Figure 1: Schematic of player, SA and ball position.

Player is seated position at G. 6 positions for the player to

hit the return shots. A, Maximum Backhand Reach

(MBR); B, Near Table Backhand (NTB); C Intermediate

Backhand Reach (IBR); D, Near Table Forehand (NTF);

E, Maximum Forehand Reach (MHR) and F, Intermediate

Forehand Reach (IFR).

The players were also measured on their maximum

tipping angle of the spine when seated (See figure

2). This tipping angle is defined as Right Tipping

Angle (RTA) and Left Tipping Angle (LTA). The

players were seated and required to perform a

maximal reach to the right and left side along the

frontal plane to the point where each player felt that

they may fall over from the side. The respective

tipping angle is defined as the angle between the

player’s spine from the seated position to the

maximal reach position on the frontal plane. The

measurement was performed using a 2-D video

analysis software (Kinovea version 0.8.15, Creative

Commons Attribution) with video footage taken

from a camera placed directly behind the players

while executing the reach.

Figure 2: Schematic of maximum reach to right on frontal

plane from original position to tipping position. Tipping

angle is measured with reference to spine between the 2

positions.

After the static measurements, all the players were

required to perform forehand and back hand strokes

shots on balls placed in 6 different positions along

the perimeter defined by each individual player.

Using the marking as a guide, the table tennis balls

were propped up to 40mm high and positioned on

designated positions along this perimeter. The

strokes were made in succession over 5 trials and the

players were required to hit the ball over the net and

land it on the opposite table like a table tennis game.

This sequence of movement aims to replicate the full

table area covered around the table by players in a

rally during competition. The task starts from near

to far table as a measure of their manoeuvrability

within their functional reach range. The time taken

to complete the task is the Sweep Time (ST).

There were 6 positions and each position is meant

for the player to execute a forehand or backhand

Net

Centre Line

Direction of play

Original

Position

Tipping

Position

Tipping

Angle

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

170

return to the opponent’s half. The return was

deemed successful when 3 consecutive balls can be

returned from that location; otherwise it would be

brought closer to the point in which the player is

able to perform the shot. The successful return

positions are subsequently defined as: Maximum

Forehand Reach (MFR), Maximum Backhand Reach

(MBR), Intermediate Forehand Reach (IFR),

Intermediate Backhand Reach (IBR), Near Table

Forehand (NTF) and Near Table Backhand (NTB).

To reduce the learning effect of the trial, players

were given sufficient time to practise the hitting the

sequence of shots until they were ready for a timed

session.

3.2 Statistical Analysis

This is an exploratory study on a special population

where the existing sample size is very limited. A

non-parametric Kruksal-Wallis and Mann-Whitney

U-test was performed on the 2 groups of participants

at α=0.05 on SA, POT, ST, RTA and LTA.

4 RESULTS

The results are presented in Table 1 for Class 1 and

2 players. The SA for all participants was found to

be less than 50% of POT from the stationary

position. The Class 1 players understandably have

the lowest SA compared to the Class 2 participants.

This applies to total ST when compared to the same

group of players.

Table 1: Table of Results for Para table tennis reach

parameters.

Class 1, n=3 Class 2, n=3

Average SA,m

0.56±0.08 0.64±0.04

POT, % 26.9 30.5

Average ST, s

4.92±0.98 3.69±0.58

Average right tipping

angle, RTA, °

20.7±4.78⁺ 49.3±8.06⁺

Average left tipping angle

LTA,°

22.0±2.94 36.0±11.9

* Kruskal-Wallis test, p=0.05 between all three groups of

players.

⁺

Denotes significance in Mann-Whitney test, p=0.05

between Class 1 and Class 2 players.

Significant differences were not found using the

Kruskal-Wallis test for all the test parameters in the

three groups.

Difference between Class 1 and 2 players’ RTA was

found to be marginally significant (p = 0.05) using

the Mann-Whitney U-test. (Although the Kruskal-

Wallis test did not show significance (p = 0.078) for

RTA). From the 9 pairs derived base on three

participants each from Class 1 and 2 players, the

rank-biserial correlation r, calculated using the

Wendt formula was equal to 1 for RTA showing the

correlation (Kerby, 2014).

From the results there is an indication that RTA

as a differentiating factor between the 2 Classes of

players.

5 DISCUSSION

5.1 Quantification of Result and

Functional Requirement

This study has provided a quantitative platform on

the ability of para table tennis players to complete a

series of movement on the basis of their functional

reach range.

In RTA where there are significant differences

between Class 1 and 2 players, the contribution may

be made by the class 2 player’s higher wrist, elbow

and shoulder strength compared to the other group.

Another possible contribution can come from a

particular Class 2 player who wears a chest strap

during training and competition as a safety device.

The chest strap used is elastic, allows the player to

lean his weight fully to extend the reach.

For future studies, the anthropometrical

contribution of each athlete should be taken into

consideration, particularly the arm length. It is

possible that this variable may influence SA

measurements and subsequently inter participant

data.

What was not expected is that ST for all players

were not significantly different. A likely explanation

would be the normalising effect of the SA between

the 2 groups of participants. With the Class 1 players

having a lower SA, effort by Class 1 players can be

considered higher as they took approximately the

same time to complete the reach task within a

smaller area. In addition, the arm length of each

player was not taken into consideration during this

study. The contribution of the arm length may

possibly have an effect on both SA and ST but ST

may increase as load on arms may increase as a

result of the increased arm length. Normalising the

ST and SA into a ratio in table 2, the ratio expresses

the rate of area coverage by each classification of

players. This ratio can possibly be a useful

A Case Study of Para Table Tennis Athlete’s Functional Ability

171

descriptor and estimate on each player’s ability,

which in turn be training targets to achieve a higher

ratio to reflect a more effective area coverage by a

player.

Table 2: SA and ST ratio for 2 groups of players.

Class 1, n=3 Class 2, n=3

Average SA,m

0.560 0.640

Average ST, s 4.92 3.69

SA/ST ratio 0.114 0.173

More data points are required to explore the

relationship between SA and ST. The reality of the

game requires players to have good functional reach

to allow them to make tactical switch between

forehand and backhand movement (Huang et al.,

2010). These results can provide the basis for

training intervention for the coaches to monitor the

players’ reach ability and agility around the table.

Any physical conditioning work or therapy to

improve their joint range can be assessed if it

translates into improved functional range and agility.

5.2 Future Work

5.2.1 Coaching Application

The authors intend to extend the test to more

participants to subsequently refine the test method to

enhance its reliability. For the functional assessment

to be readily accepted during training by both

coaches and players, a simple operational procedure

is essential. The authors are exploring how the test

can be implemented via a digital device to achieve

this goal.

In terms of a training test set, coach and players

would have a quantitative platform to assess the

reach ability for a new or existing player. Together

with targeted strength and flexibility training, the

kinematic quantification provides a clear objective

for the team to act on. In addition, the data can be

used to assess the reach ability of opponents during

competition.

The study has provided a framework to quantify

the movement and ability of Class 1 and 2 Para

Table Tennis players. The methods are designed

with practicality of implementing the assessment

during training, so that it is possible to conduct when

required by coaches.

Despite participants being grouped into the two

classification groups, the ability of the participants

within each group do vary. For future work we

intend to perform test-retest reliability analysis to

determine the efficacy of this test for this population

group.

5.2.2 Concept Chair

Key parameters which the concept chair can

improve would be SA and ST for Class 1 and 2

players. Results of this study will be used as a

benchmark of the players’ current ability with their

existing competition chair. The information will then

be compared against any equipment modification to

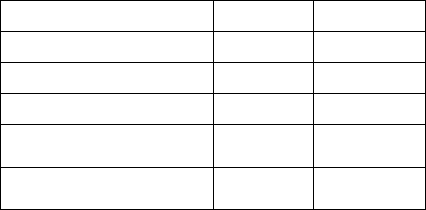
improve the players’ SA and time. Figure 2

illustrates a concept chair with possible

improvement for anchoring the players’ arms during

play, rotational movements and anti-tipping

measures.

The first concept is to explore the impact of seats

on the players. The players are all using a fabric

covered foam type seat, where the functionality is

targeted at improving comfort during day to day use

instead of competitive table tennis. The authors are

exploring different methods to improve this interface

to increase the angular speed of the players’ torso

during play. For Class 1 players who have limited

control over their torso, the solution needs to assist

the player to move while seated.

Another possible conceptual solution is to

modify the existing push handle of the player’s

chair. This is illustrated in Figure 2. This

modification is expected to allow players to anchor

on the chair to improve the range of RTA and LTA.

Although players are already anchoring on the

existing chair handle, the new conceptual solution

aims to improve on the placement of this handle on

the chair.

Figure 3: Visualisation of concept chair with

modified push handle.

icSPORTS 2015 - International Congress on Sport Sciences Research and Technology Support

172

Lastly the third concept that the authors are looking

at is implementing is a safety hand rest for the

players. Toppling over the chair during the game is

a real situation during the game when the players

over reach. Some form of safety anchor apart from

the push handle is necessary to prevent side tipping.

With the anchor, the authors hope to provide the

players with more confidence during play when

reach to the sides.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the

assistance rendered by the Singapore Disability

Table Tennis Association during this study.

REFERENCES

Bernardi, M., Janssen, T., Bortolan, L., Pellegrini, B.,

Fischer, G., & Schena, F., 2013, 'Kinematics of cross-

country sit skiing during a Paralympic race', Journal

Of Electromyography & Kinesiology, 23, 1, pp. 94-

101 8p.

Dingley, A., Pyne, D., & Burkett, B 2014, 'Phases of the

Swim-start in Paralympic Swimmers are Influenced by

Severity and Type of Disability', Journal Of Applied

Biomechanics, 30, 5, pp. 643-648.

ITTF Para Table Tennis Division, ITTF Classification

Code Federation, I. T. T. (2010). ITTF-Classification-

Code-final. Retrieved June 1, 2015, from

http://www.freewebs.com/wasusa/Table%20Tennis/IT

TF-Classification-Code-final-March-2010.pdf.

Hegde, E., & Standal, Ø. F. (2013). Learning to become a

team player. Situated learning in Paralympic Sledge.

European Journal of Adapted Physical Activity, 6(1),

30-42.

Huang, C.-H., Hsiao Tsun, I., Kuo, M.-C., & Hsieh, H.-J.

(2010). Survey analysis for the current utilization

status of wheelchair table tennis athletic equipments.

International Table Tennis Federation Sports Science

Congress Conference Proceedings(6), 235-238.

Kerby, D. D. (2014). The simple difference formula: an

approach to teaching nonparametric correlation.

Innovative Teaching, 3(1), 1-9. doi:10.2466/11.IT.3.1.

Borges M., Sousa E., Rego J., Medeiros R., Spina M.,

Cabral B., & Dantas, P. (2014). EMG analysis of

bench press in paralympic athletes. Medicina Sportiva,

10(no 4), 2452-2456. Retrieved from: http://www.

medicinasportiva.ro/SRoMS/RMS/40/Electromyograp

hic-bench-press-paralympic-athletes.pdf.

A Case Study of Para Table Tennis Athlete’s Functional Ability

173