Si elegans: A Computational Model of C. elegans Muscle Response

to Light

Alicia Costalago Meruelo, Pedro Machado, Kofi Appiah and T. M. McGinnity

School of Science and Technology, Nottingham Trent University, Nottingham, U.K.

Keywords: Si elegans, Phototaxis, Modelling, Muscle, Sensory Neurons C. elegans, Izhikevich Neuron Model.

Abstract: It has long been the goal of computational neuroscientists to understand animal nervous systems, but their

vast complexity has made it very difficult to fully understand even basic functions such as movement. The C.

elegans nematode offers the opportunity to study a fully described connectome and link neural network to

behaviour. In this paper a model of the responses of the body wall muscle in C. elegans to a random light

stimulus is presented. An algorithm has been developed that tracks synapses in the nematode nervous system

from the stimulus in the phototaxis sensory neurons to the muscles cells. A linear second order model was

used to calculate the isometric force in each of the C. elegans body wall muscle cells. The isometric force

calculated resembles that of previous investigations in muscle modelling.

1 INTRODUCTION

Using computational neuroscience models, one can

simulate the nervous system by simplifying brain

models into neural circuits to attempt to understand

behaviour. There have been huge advances in

understanding the operations of neurons at a cellular

and sub-cellular level, as well as the operations of

large scale neural networks (Boyle and Cohen, 2007).

However, typically artificial neural networks are

highly simplified models of the individual neurons

they represent and do not have any neural structure in

mind or refer to the nervous systems of any particular

species (Cangelosi, 1997).

In this paper, we present a neural model of the

muscle cells in the nematode Caenorhabditis elegans

(C. elegans). C. elegans (Fig. 1) is a small soil

nematode, with a simple anatomy comprising of

about 1000 cells, 302 neurons, 135 muscle cells and

about 8000 synapses (Altun and Hall, 2009a). The

anatomical description of the whole animal has been

completed at the electron microscopy level, making

the worm an important model for research in many

fields (Brenner, 1973; Wood, 1988). The adult

hermaphrodite consists of a mere 302 neurons, with

their connectivity already well described, making it a

model system for advancing the connectome program

(Varshney et al., 2011). Unfortunately, far less

information is available on the properties of these

neurons (Boyle and Cohen, 2007).

Figure 1: C. elegans anatomy, including the head, intestine

and tail (Altun and Hall, 2009a).

The C. elegans nervous system is sufficiently rich

to generate a large set of behaviours, including

locomotion (Gjorgjieva et al., 2014), touch response

Chalfie et al., 1985), detection of chemicals,

temperature and light gradients (Dunn et al. 2004;

Rankin, 2002; Ward et al., 2008) even memory has

been observed (Lin and Rankin, 2010).

Movement, or locomotion, in the worm typically

consists of periods of forward motion interspersed

with short periods of backward motion and turns,

controlled by a subset of its nervous system (Boyle

and Cohen, 2007). A number of models have been

developed for the C. elegans locomotion, yet it is still

partially understood and remains significantly

challenging to modellers and experimentalists

(Bryden, 2004; Suzuki et al., 2005).

The worm also exhibits escape responses to

external stimuli. A gentle touch with a fine hair

around the head area will cause the worm to move

backwards and a touch in the tail causes the worm to

Tail

Head

Intestine

Meruelo, A., Machado, P., Appiah, K. and McGinnity, T..

Si elegans: A Computational Model of C. elegans Muscle Response to Light.

In Proceedings of the 3rd International Congress on Neurotechnology, Electronics and Informatics (NEUROTECHNIX 2015), pages 121-126

ISBN: 978-989-758-161-8

121

move forward (Chalfie et al., 1985). The worm has

the ability to orient in response to gradients of

chemical concentration also referred to as chemotaxis

(Bargmann and Horvitz, 1991). Chemotaxis is used to

locate food and males use it to locate hermaphrodites.

This has been studied by establishing a two-

dimensional gradient chemical concentration,

demonstrating that chemotaxis behaviour in the worm

is consistent with true orientation of the chemical

gradient (Morse et al., 1998). Other behaviour

exhibited by the worm is the ability to move into

regions with constant or gradient temperatures. The

worm is known to migrate to regions with desirable

temperatures and deviates from undesirable

temperatures by sudden switches in direction

(Hedgecock and Russell, 1975).

Another behaviour recently observed in C.

elegans is phototaxis, which is the ability to sense and

react to light. A series of sensory neurons located in

the worm’s head are able to detect light stimuli and

they elicit a robust avoidance response (Ward et al.,

2008). The worm is known to lack specialised light-

sensing organs and lives in dark soil, yet it possesses

a simple way of detecting light which induces

avoidance behaviour mediated by a group of

chemoreceptive neurons (Ward et al., 2008). Light

stimuli evoke negative responses in the worm and

drive it back to a dark environment. If exposed to light

when moving forward, it would stop and then initiate

reversal. Similarly, the worm stops moving

backwards when exposed to light and starts moving

forward. This behaviour serves as a survival

mechanism in the soil.

In this paper we provide an initial model of the

responses to light of the C. elegans. It is being

developed as a test bed for the European Si elegans

project. The European Si elegans project intends to

provide an open-access and user-friendly framework

for the accurate emulation of the C. elegans nervous

system (Blau et al., 2014). It will provide a

sophisticated emulation environment with an

advanced design environment where users can design

their own custom neuron models, or use models from

a model library, run and visualise the emulation

results on a unique 3D virtual arena. The emulation

will run on a hardware parallel architecture based on

field programmable gate arrays (Machado et al.,

2015).

2 METHODS

2.1 Network Pathway

Light stimulates a series of sensory neurons situated

in the head of the nematode, which in turn excite a

series of interneurons and motor neurons, creating a

neural network. Some of these motor neurons

innervate 95 body wall muscles that run along the

body of the C. elegans (Fig. 2) (Hresko et al., 1994;

Varshney et al., 2011; White et al., 1986). When a

light source is focussed on the worm’s head, the

sensory neurons trigger a burst of neuronal activity

that results in muscle contractions and relaxations

which guide the nematode away from the light source.

This network then produces the light-induced head

avoidance response known as negative phototaxis

(Ward et al., 2008).

Figure 2: Body wall muscles of the C. elegans, divided into

four quadrants, from head to tail. Adapted from Altun &

Hall (2009).

We have elavorated a Matlab

algorithm that

follows the synapses from the sensory neurons

stimulated by light to each of the motor neuron

connected to body wall muscles. Through this

algorithm the neural pathways to each of the 95 body

wall muscles have been calculated, providing a

representation of a network that reflects the actual

neural connections of the worm, including the

weights of such connections. The connections and

weights between individual neurons in the C. elegans

have already been described (Hresko et al., 1994;

NeBICA 2015 - Symposium on Neuro-Bio-Inspired Computation and Architectures

122

Varshney et al., 2011), and the algorithm is able to

use this information and track the synapses from the

sensory neurons to the interneurons and motor

neurons. From all possible pathways calculated, only

those targeting specific motor neurons that innervate

the body wall muscles are selected.

The algorithm also allows the selection of the

depth in the network to observe either direct pathways

between sensory to motor neurons, networks with one

layer of interneurons or larger networks. Further

details about the neurons and muscles models are

given in the next two sections.

2.2 Neuron Model

To model the sensory neurons, interneurons and

motor neurons, an Izhikevich spiking neural model is

implemented (Izhikevich, 2003). In this particular

case, we are making the assumption that all neurons

behave equally (i.e. all share the same model), even

though C. elegans is thought to have no spiking

neurons (Lockery and Goodman, 2009).

The Izhikevich neural model combines the

biologically plausibility of Hodgkin-Huxley type

dynamics and the computational efficiency of

integrate-and-fire neurons (Izhikevich, 2003). It

follows a system of differential equations of the form:

 =0.04



+5+140−+

 =(−)

If ≥30 mV, then 

←

←+

(1a)

(1b)

(1c)

In these equations, the variables  and  represent

the membrane potential and the recovery variable

respectively, I is the injected dc current,  is the time

scale of the recovery variable,  is the sensitivity of

the recovery variable,  is the after-spike reset value

of the membrane potential caused by high-threshold

potassium conductance and  is the after-spike reset

value of the membrane potential caused by low-

threshold potassium conductance.

The parameters were set to typical values: =

0.02 , b =0.2, =−65 mV, =2 (Izhikevich,

2003). In order to consider both excitatory and

inhibitory motor neurons responses, the inhibition has

been simplified to a negative current of the same

amplitude as its excitatory counterpart.

2.3 Muscle Model

To model the muscle responses to motor neuron

inputs, an isometric model has been chosen. Isometric

models calculate the force of contraction of a muscle

when no output movement is produced (Windmaier

et al., 2003).

A second order linear model (Bobet et al., 1993)

was used to model the isometric force, since linear

models are attractive due to their simplicity and ease

of analysis. However, they have to be considered

carefully, as they may lead to loss of information and

might not provide a good description of muscle force

(Bobet et al., 2005).









(



)

+







(



)

+

(



)

=





(



)

(2)

Where 

(



)

is the muscle force as a function of

time, 



are the model parameters and () is the

input spike train coming from the motor neurons. For

this particular test, the values chosen are 



= 0.004,





=0.26 and 



= 0.023, based on the model fitted

to an invertebrate muscle response (Wilson et al.,

2012), since no data is available to fit the model to the

C. elegans.

3 RESULTS

3.1 Phototaxis Network Pathway

The pathways from the sensory neurons receiving

phototaxis to the motor neurons that innervate the

body wall muscles have been calculated using the

algorithm developed.

To provide an example, the connections to the

muscle MDR05 (Muscle Dorsal Right number 05), at

the neck of the worm, are described. In this particular

case, there are four sensory neurons (AWBR, ASKR,

ASHL, ASHR) that synapse directly with the muscle

motor neurons (RMGR, RIML). By increasing the

depth and adding connections through interneurons,

there are connections to 20 interneurons from all the

14 sensory neurons excited by light. These

interneurons synapse to five motor neurons that

innervate the muscle, producing a total of 100

different pathways (Fig. 3). Adding a second layer of

interneurons would form a four layer network, with a

total of 1848 pathways and 98 different neurons

involved.

As the number of layers increases, so does the

number of connections and neurons involved,

increasing the complexity of the network. For this

analysis, the number of layers is restricted to three,

analysing a network with a single interneuron.

In the case of the network to innervate muscle

MDR05, most of the connections are found in the

neck and head of the nematode, with a few exceptions

in the rest of the body (Fig. 3)

Si elegans: A Computational Model of C. elegans Muscle Response to Light

123

Figure 3: a) Representation of the C. elegans nematode including the positions of the sensory neurons, interneuron and motor

neurons in the example calculated from phototaxis sensory neurons to the muscle MDR05 with a single interneuron layer. b)

Network pathway example calculated to the muscle MDR05.

Figure 4: Number of synapses from motor neuron to each

of the body wall muscles, where MDL stands for Muscle

Dorsal Left, MDR for Muscle Dorsal Right, MVL for

Muscle Ventral Left and MVR for Muscle Ventral Right.

The fact that most neurons and pathways are near the

head of the nematode is not limited to the network of

muscle MDR05. The muscles in the head and neck

and on the top half of the body are the ones which

received most inputs from the sensory neurons (Fig.

4). Considering that the phototaxis sensitive neurons

are situated near the head, it is possible that this dense

interconnectivity in the top half is due to network

optimisation to minimise wiring cost (Chen et al.,

2006).

3.2 Responses of Body Wall Muscles to

Light

Using the pathway calculated for each body wall

muscle, an artificial neural network has been created

using the Izhikevich neural model (Izhikevich, 2003).

The random stimulus in the sensory neurons is

transmitted through the network to the motor neurons,

where the input spike train to the muscle is created.

Using the linear model described in Section 2.3,

the isometric force produced by each of the 95 body

wall muscles is calculated. Following the previous

example, the response of muscle MDR05 to a random

stimulus is as shown in Figure 5.

123456789101112131415161718192021222324

Head Neck Body

Number of input synapses

Muscle cell

MDL

MDR

MVL

MVR

Average

Intestine

Phar

Tail

Mouth

Sensor

Neurons

Motor Neurons

Muscle

Interneurons

NeBICA 2015 - Symposium on Neuro-Bio-Inspired Computation and Architectures

124

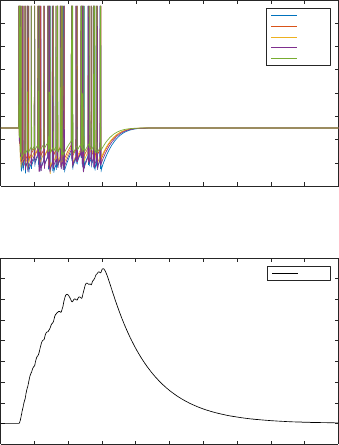
Figure 5: Spike train from the motor neurons and isometric

force calculated for the example muscle MDR05.

The force calculated in the body wall muscles can

be translated into muscle contraction and,

furthermore, into movement. Many investigators

have provided different models to achieved this

(Boyle et al., 2012; Bryden and Cohen, 2008; Bryden,

2004), however, in this particular piece of work, the

translation has not been performed.

4 CONCLUSIONS AND FUTURE

WORK

In this paper we have presented an algorithm and a

cascade of models to simulate the force produced in

the C. elegans body wall muscles in response to a

random light stimulus.

The algorithm developed is able to read the

information on the connections for each neuron and

follow those connections to the motor neurons

connected to the body wall muscles. This way we

have created a representation of the network that

reflects the actual neural connections of the worm.

This pathway was effectively used in producing an

Artificial Neural Network, using Izhikevich neural

models, which transmitted the random stimulus to the

muscle cell.

The isometric force calculated with the stimulus

transmitted through the network provides an

approximation of the behaviour of the body wall

muscles that could be translated into locomotion.

Due to the lack of neuromuscular recordings and

since the simulation of locomotion has not yet been

performed, it is difficult to assess the accuracy of the

force obtained. The shape of the isometric force is

however comparable to that of other works simulating

C. elegans body wall muscle (Boyle and Cohen,

2008), other animals (Wilson et al., 2012) and even

human muscle force (Hunt et al., 1998).

This paper presents an early stage investigation.

Future work in this system includes that of the model

of phototaxis sensitive sensory neurons responding to

specific light amplitudes and frequencies (Ward et al.,

2008). Furthermore, the artificial neural network used

standard Izhikevich spiking neural models

(Izhikevich, 2003) for all neurons involved in the

network. Specific models for each of the neurons will

be implemented in future work approximating more

accurately the behaviour of the neurons involved in

this system in the C. elegans.

An implementation of this system into the Si

elegans framework to simulate the output movement

in response to light among other behaviours has

already started. This implementation would provide

an answer to whether the models presented here are

accurate enough to produce simulated C. elegans

avoidance in the presence of light. Therefore, the

models will need to be implemented into the

hardware framework forming the Si elegans project.

ACKNOWLEDGEMENTS

The research leading to these results has been

supported by the Si elegans project, which has

received funding from the European Community’s

7th Framework Programme under the Neuro

BioInspired Systems Project Grant agreement

601215.

REFERENCES

Altun, Z.F., Hall, D.H., 2009a. Introduction [WWW

Document]. WormAtlas. URL www.wormatlas.org

(accessed 9.2.15).

Altun, Z.F., Hall, D.H., 2009b. Muscle System, somatic

muscle [WWW Document]. WormAtlas. URL

www.wormatlas.org (accessed 9.2.15).

Bargmann, C.I., Horvitz, H.R., 1991. Chemosensory

neurons with overlapping functions direct chemotaxis

to multiple chemicals in C. elegans. Neuron 7, 729–742.

Time [s]

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

Spike voltage (mV)

-120

-100

-80

-60

-40

-20

Input spikes

RIML

RMGR

SMDDL

RMDR

AS01

Time [s]

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

Isometric force (%)

-0.1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

MDR05

Si elegans: A Computational Model of C. elegans Muscle Response to Light

125

Blau, A., Callaly, F., Cawley, S., Coffey, A., De Mauro, A.,

Epelde, G., Ferrara, L., Krewer, F., Liberale, C.,

Machado, P., Maclair, G., McGinnity, T.-M., Morgan,

F., Mujika, A., Petrushin, A., Robin, G., Wade, J., 2014.

The Si elegans Project – The Challenges and Prospects

of Emulating Caenorhabditis elegans. In: Duff, A.,

Lepora, N., Mura, A., Prescott, T., Verschure, P.M.J.

(Eds.), Biomimetic and Biohybrid Systems SE - 54,

Lecture Notes in Computer Science. Springer

International Publishing, pp. 436–438.

Bobet, J., Gossen, E.R., Stein, R.B., 2005. A comparison of

models of force production during stimulated isometric

ankle dorsiflexion in humans. IEEE Trans. Neural Syst.

Rehabil. Eng. 13, 444–451.

Bobet, J., Stein, R.B., Oguztoreli, M.N., 1993. A Linear

Time-Varying Model of Force Generation in Skeletal-

Muscle. IEEE Trans. Biomed. Eng. 40, 1000–1006.

Boyle, J.H., Berri, S., Cohen, N., 2012. Gait Modulation in

C. elegans: An Integrated Neuromechanical Model.

Front. Comput. Neurosci. 6.

Boyle, J.H., Cohen, N., 2007. The role of body wall muscles

in C. elegans locomotion. In: BioSystems. p. 363.

Boyle, J.H., Cohen, N., 2008. Caenorhabditis elegans body

wall muscles are simple actuators. BioSystems 94, 170–

181.

Brenner, S., 1973. The genetics of behaviour. Br. Med. Bull.

29, 269–271.

Bryden, J., Cohen, N., 2008. Neural control of

Caenorhabditis elegans forward locomotion: The role

of sensory feedback. Biol. Cybern. 98, 339–351.

Bryden, J.A., 2004. A simulation model of the locomotion

controllers for the nematode Caenorhabditis elegans.

Cangelosi, A., 1997. A neural network model of

caenorhabditis elegans: the circuit of touch sensitivity.

Neural Process. Lett. 6, 91–98.

Chalfie, M., Sulston, J.E., White, J.G., Southgate, E.,

Thomson, J.N., Brenner, S., 1985. The neural circuit for

touch sensitivity in Caenorhabditis elegans. J. Neurosci.

5, 956–964.

Chen, B.L., Hall, D.H., Chklovskii, D.B., 2006. Wiring

optimization can relate neuronal structure and function.

Proc. Natl. Acad. Sci. U. S. A. 103, 4723–4728.

Dunn, N.A., Lockery, S.R., Pierce-Shimomura, J.T.,

Conery, J.S., 2004. A neural network model of

chemotaxis predicts functions of synaptic connections

in the nematode Caenorhabditis elegans. J. Comput.

Neurosci. 17, 137–147.

Gjorgjieva, J., Biron, D., Haspel, G., 2014. Neurobiology

of caenorhabditis elegans locomotion: Where do we

stand? Bioscience 64, 476–486.

Hedgecock, E.M., Russell, R.L., 1975. Normal and mutant

thermotaxis in the nematode Caenorhabditis elegans.

Proc. Natl. Acad. Sci. U. S. A. 72, 4061–4065.

Hresko, M.C., Williams, B.D., Waterston, R.H., 1994.

Assembly of body wall muscle and muscle cell

attachment structures in Caenorhabditis elegans. J. Cell

Biol. 124, 491–506.

Hunt, K.J., Munih, M., Donaldson, N., Barr, F.M.D., 1998.

Investigation of Hammertein Hypothesis in the

Modelling of Electrically Stimulated Muscle. IEEE

Trans. Biomed. Enginering 45.

Izhikevich, E.M., 2003. Simple model of spiking neurons.

IEEE Trans. Neural Netw. 14, 1569–72.

Lin, C.H., Rankin, C.H., 2010. Nematode learning and

memory: neuroethology, Encyclopedia of Animal

Behavior. Elsevier.

Lockery, S.R., Goodman, M.B., 2009. The quest for action

potentials in C. elegans neurons hits a plateau. Nat.

Neurosci. 12, 377–8.

Machado, P., Wade, J.J., Appiah, K., McGinnity, T.M.,

2015. Si elegans: Hardware Architecture

and Communications Protocol. In: The 2015

International Joint Conference on Neural Networks.

IEEE, pp. 3473–3479.

Morse, T.M., Lockery, S.R., Ferree, T.C., 1998. Robust

Spatial Navigation in a Robot Inspired by Chemotaxis

in Caenorhabditis elegans. Adapt. Behav. 6, 393–410.

Rankin, C.H., 2002. From gene to identified neuron to

behaviour in Caenorhabditis elegans. Nat. Rev. Genet.

3, 622–30.

Suzuki, M., Tsuji, T., Ohtake, H., 2005. A model of motor

control of the nematode C. elegans with neuronal

circuits. Artif. Intell. Med. 35, 75–86.

Varshney, L.R., Chen, B.L., Paniagua, E., Hall, D.H.,

Chklovskii, D.B., 2011. Structural properties of the

Caenorhabditis elegans neuronal network. PLoS

Comput. Biol. 7, e1001066.

Ward, A., Liu, J., Feng, Z., Xu, X.Z.S., 2008. Light-

sensitive neurons and channels mediate phototaxis in C.

elegans. Nat. Neurosci. 11, 916–922.

White, J.G., Southgate, E., Thomson, J.N., Brenner, S.,

1986. The Mind of a Worm. Philos. Trans. R. Soc. B

Biol. Sci. 314, 1–340.

Wilson, E., Rustighi, E., Newland, P.L., Mace, B.R., 2012.

A comparison of models of the isometric force of locust

skeletal muscle in response to pulse train inputs.

Biomech. Model. Mechanobiol. 11, 519–532.

Windmaier, E., Raff, H., Strang, K., 2003. Human

Physiology: The Mechanisms of Body Functions. The

McGraw−Hill Companies.

Wood, W.B., 1988. Introduction to C. elegans Biology. The

Nematode Caenorhabditis elegans 1–16.

NeBICA 2015 - Symposium on Neuro-Bio-Inspired Computation and Architectures

126