
Establishing a Framework for Managing Interest in Technical Debt
Areti Ampatzoglou, Apostolos Ampatzoglou, Paris Avgeriou
Department of Mathematics and Computer Science, University of Groningen, Netherlands
areti.ampatzoglou@rug.nl, a.ampatzoglou@rug.nl, paris@cs.rug.nl
Alexander Chatzigeorgiou
Department of Applied Informatics, University of Macedonia, Thessaloniki, Greece
achat@uom.gr
Keywords: Technical debt, Architecture, Software quality, Iinterest.
Abstract: Technical debt (TD) has gained significant attention over the past years. Due to its interdisciplinary nature, it
has become attractive for both technical and management stakeholders, to acknowledge and discuss issues
related to decayed design-time qualities over time, and their corresponding consequences. Until now, despite
the inherent relevance of technical debt management to economics, the TD research community has not suf-
ficiently exploited economical methods/models. Therefore, in this paper we present a framework for manag-
ing interest in technical debt, founded on top of well-known economic theories (i.e., Loanable Funds and
Liquidity Preference Theory) and current TD research. Specifically, in our framework, we will discuss aspects
related to technical debt interest, such as: types of TD interest, TD interest characteristics, and a proposed TD
interest theory. Finally, in order to boost the amount of empirical studies in TD research, we will propose
several tentative research designs that could be used for exploring the notion of interest in technical debt
practice.
1 INTRODUCTION
The term Technical Debt (TD) was coined in 1992 by
Ward Cunningham (1992) to describe the technical
compromises being made while coding, in order to
speed up product delivery and meet release deadlines.
Research on technical debt is rapidly growing over
the last years, since around 90% of articles on the sub-
ject have been published after 2010 (Li et al., 2015).
Similarly to its success among academics, TD seems
to be a topic that is appealing for practitioners, as
well. Specifically, according to Li et al. (2015), from
the current corpus of research efforts in technical
debt, 43% is performed in academia, 40% in industry
and 17% in both.
Apart from the fact that TD is a problem of para-
mount importance for software development, another
possible explanation for its popularity, in both aca-
demia and industry, is its interdisciplinary nature
(software engineering and economics), which facili-
tates the communication among technical and man-
agement stakeholders (Ampatzoglou et al., 2015). To
achieve this, the TD community borrows terms from
economics and maps them to software engineering
ones. Based on two recent literature reviews on the
subject (Ampatzoglou et al., 2015 and Li et al., 2015),
the two most frequently used financial terms in TD
research are: interest and principal.
Principal is a clearly defined concept, which is
characterized as the effort required to address the dif-
ference between the current and the optimal level of
design-time quality, in an immature software artefact
or the complete software system (Ampatzoglou et al.,
2015). Therefore, it is quantifiable and, in general, a
commonly accepted concept. On the other hand, in-
terest (associated with many definitions, which in
some cases are controversial) cannot be measured in
a straightforward way, since it involves the valuation
of future maintenance activities. Measuring interest
becomes even more complicated due to the fact that
its occurrence is not certain, in the sense that extra
cost/effort might not be required, and therefore inter-
est will not need to be paid off.
Additionally, research on TD interest and TD in
general, appears to lack empirical evidence. Accord-
ing to Li et al. (2015) 49% of the complete corpus of
TD research presents no empirical evidence, or only
toy examples, whereas this number rises to 56%,
75
Ampatzoglou A., Ampatzoglou A., Avgeriou P. and Chatzigeorgiou A.
Establishing a Framework for Managing Interest in Technical Debt.
DOI: 10.5220/0005885700750085
In Proceedings of the Fifth International Symposium on Business Modeling and Software Design (BMSD 2015), pages 75-85
ISBN: 978-989-758-111-3
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

when focusing on interest (Li et al., 2015).
To partially alleviate these problems, in this study
we investigate the notion of interest as it is applied in
the TD domain; our goal is to propose FItTeD, i.e., a
Framework for managing Interest in Technical Debt.
The FItTeD framework, aims to:
(G1) Identify types of TD interest, when it occurs,
and the high-level structure of its calculation.
Identifying the types of interest, which can oc-
cur along evolution, is the first step towards
more formal Technical Debt Management
(TDM). Until now, the definitions of interest
are rather high-level, and interest measurement
is often not applied in practice.
(G2) Explore how various characteristics of interest
in economics apply in TD interest. An example
of such a characteristic is whether interest is
simple or compound. However, these charac-
teristics have not been fully exploited in re-
search state-of-the-art, yet.
(G3) Propose a TD interest theory
. Until now, no
study has used the economic interest theories
for modelling technical debt interest. We will
rely on the Liquidity Preference Theory, for
modelling the evolution of TD.
The cornerstones for the development of FItTeD are:
The corpus of existing research on Technical
Debt Management (TDM). We intend to reuse the
primary studies identified in a Systematic Litera-
ture Review (SLR) on technical debt by Am-
patzoglou et al. (2015), and filter them so as to ex-
tract primary studies related to interest, and syn-
thesize them in a systematic way (Kitchenham et
al., 2009).
The existing economic interest theories. We in-
tend to apply existing economic interest theories,
i.e., the Loanable Funds and the Liquidity Prefer-
ence Theory, to reuse existing knowledge from
economics, on how interest should be handled,
and learn from accumulated experiences.
This framework aims at supporting software engi-
neers to determine the change of technical debt
amount in the future, by holistically describing all pa-
rameters that affect its future value (i.e., repayment,
interest, additional debt, etc.). This can in turn allow
the use of elaborate financial methods in several tech-
nical debt management activities, i.e., repayment,
monitoring, and prioritization. Additionally, we ex-
pect that the proposed framework can boost empirical
research in the field of TD, in the sense that it can
facilitate a common understanding on TD interest and
point to interesting research directions.
The rest of the paper is organized as follows: In
Section 2, we present related work from the field of
economics, i.e., the dominant interest theories. Next,
in Section 3, we will present the outcome of revisiting
the primary studies of the SLR by Ampatzoglou et al.
(2015), by presenting only interest-related infor-
mation. In Section 4, we present the proposed frame-
work for managing interest in technical debt. In Sec-
tion 5, we discuss possible ways that our framework
can be used for boosting empirical research in the
field of TD. Finally, in Sections 6 and 7, threats to
validity and conclusions are presented.
2 INTEREST IN ECONOMICS
Regarding the way interest rate is defined in the mar-
ket; various models have been suggested, by different
schools of economics (Mishkin and Eakins, 2012).
The mainstream theories are the Loanable Funds The-
ory, developed by the neoclassical school, and the Li-
quidity Preference Theory, proposed by the Keynes-
ian theory (Mishkin and Eakins, 2012).
Interest rate is the price paid for borrowing money
or vice versa (the payment received to loan money).
Therefore it can be considered as the price of money.
Interest rate, as any other price, can be defined in the
market at the equilibrium between supply and de-
mand. According to the Loanable Funds Theory, in-
terest rate specification takes place in the market of
loanable funds. On the one hand, individuals or enter-
prises, who want to invest, form the demand for loan-
able funds. They ask for loans in order to proceed
with an investment. As interest rate gets higher, bor-
rowing becomes more expensive. As a result, demand
for loanable funds decreases as interest rate increases.
On the other hand, the supply of loanable funds
comes from people or enterprises that use the loana-
ble funds market to save their money. Instead of con-
suming part of their income, they choose to put it into
the loanable funds market in order to save it for later.
In this case, higher interest rate means higher return
on savings. Therefore, supply of loanable funds rises
as interest rate increases.
In the diagram of Figure 1, the equilibrium in
loanable funds market is presented. We note that, in
economic theory, all kinds of supply – demand dia-
grams represent the dependent variable on the hori-
zontal axis and the independent variable on the verti-
cal axis. Therefore, in this case, the vertical axis de-
picts interest rate (r), while the horizontal axis repre-
sents the quantities of supply and demand for loana-
ble funds. The quantity of loanable funds supplied at
any level of interest rate is presented by line S. Line
Fifth International Symposium on Business Modeling and Software Design
76

S depicts the positive correlation between interest rate
and loanable funds supply. Likewise, the quantity of
loanable funds demanded at any level of interest rate
is presented by line I. The negative correlation be-
tween interest rate and loanable funds demand is in-
dicated by the negative slope of line I. When interest
rate is higher than r*, then it is more profitable to
save, or it is more profitable to lend than to borrow,
and supply of loanable funds is higher than demand.
On the other hand, when interest rate r is lower than
the level of r*, then it is more profitable to invest, or
it is more profitable to borrow than to lend, and de-
mand for loanable funds is higher than supply. When
r=r*, then both the investors and the savers have no
motivation to change their position in the market and
equilibrium is achieved. Consequently, interest rate is
determined at r=r*.
Figure 1: Loanable Funds Theory.
Equilibrium in the market is achieved at interest
rate r*, when every other factor, that could influence
savings or investment, is considered stable (ceteris
paribus – i.e., a Latin phrase, often used in economics
to suggest that all other factors are constant, in order
to examine the relationship between two variables).
Therefore, interest rate level may move upwards or
downwards in case of changes to savings or invest-
ments, due to exogenous factors (e.g., income). For
example, an increase in income would cause an in-
crease in the quantity of savings. That would result in
a shift to the right of the savings curve (S), which is
the supply of loanable funds. In Figure 1, the new line
S
1
depicts such a change. As shown in the diagram,
the new equilibrium is now achieved at point E
1
and
interest rate is defined at r
1
, lower than r*.
The Liquidity Preference Theory determines in-
terest rate level through the mechanism of supply and
demand for money (cash), which is performed in the
money market. In this case, supply of money (M) is
given at any point of time and is determined by the
central bank, according to the needs of the economy.
In other words, supply of money is not dependent on
interest rate and it is exogenously defined. On the
other side, demand for money (L) represents the
quantity of cash that people prefer to hold for pur-
poses of transactions, precaution or speculation. In
this case, as interest rate increases, it becomes more
profitable for people to invest money than to hold it.
Consequently, an increase in interest rate leads to a
decrease in the quantity of money demanded in the
market and a decrease in interest rate causes an in-
crease in demand for money. Similarly to the Loana-
ble Funds theory, interest rate is determined by the
equilibrium point of the market.
Figure 2: Liquidity Preference Theory.
The diagram of Figure 2 shows the equilibrium in
the market of money. Interest rate is represented on
the vertical axis, whereas money supply and demand
are shown on the horizontal axis. The supply curve is
vertical to the horizontal axis, and represents the sta-
ble money supply, provided by the central bank, in-
dependently of the interest rate level, as mentioned
above (this assumption consists the main difference
with the loanable funds theory). Demand for money
is negatively related to interest rate (because in this
case interest rate is the cost of holding money against
to investing in a bond) and line L shows the quantity
of money demanded at any given interest rate, ceteris
paribus. The intersection of the two curves, M and L,
represents market equilibrium and determines the
level of the interest rate at r*.
In case of a change in demand for money because
of a change in another determining factor, e.g. in-
come, or in case of a change in the quantity of money
supplied by the central bank, equilibrium rate will
change. For example, if the central bank decides to
increase money supply, then M would increase to M
1
and the curve in the diagram of Figure 2 would shift
Establishing a Framework for Managing Interest in Technical Debt
77

to the right. Consequently, equilibrium would be de-
fined by point E
1
and the new interest rate in the mar-
ket would be r
1
, lower than r*.
3 INTEREST IN TECHNICAL
DEBT RESEARCH
In this section we present an overview of studies that
have investigated interest in Technical Debt Manage-
ment (TDM). According to Ampatzoglou et al. (2015)
and Li et al. (2015), interest is the prominent financial
term that is used in TDM research. Note that in eco-
nomics, interest theories are used for calculating in-
terest rate (not interest per se), since interest is calcu-
lated based on interest rate. However, in TDM inter-
est is not calculated based on interest rate, but it is
assessed in various other ways, as explained later in
this section. Specifically, from TD research, it is not
clear if interest rate can be defined at all. In this study,
we reuse the dataset extracted by Ampatzoglou et al.
(2015), i.e., 29 studies that focus on TD interest. In
this paper, we are not presenting in detail the SLR
process, since it is thoroughly discussed in the origi-
nal study, but only an outline:
Queried 7 digital libraries (IEEE, ACM, Scopus,
Springer, Science Direct, Web of Science, and
Google Scholar), with the term technical debt.
The search returned 1,173 primary studies
Applied Inclusion/Exclusion Criteria (e.g., is the
study focused on the financial aspect of TD). The
process returned 69 primary studies.
From that stage and on, the process is specialized
to the goals of this paper. Specifically, first we filtered
primary studies related to interest. This step has been
performed as part of data collection in the original
SLR. Therefore, in this study we explored the 29 pri-
mary studies, which according to Ampatzoglou et al.
(2015) are relevant to interest. This set of studies is
our primary study dataset. For each study, the follow-
ing data have been extracted:
[D
1
] Interest amount definition. We record the defi-
nition that the authors provide for the amount of
interest. The term interest amount is derived by
the work of Seaman and Guo (2011), who sug-
gest that interest should be calculated by taking
into account two components interest amount
and interest probability (see D2).
[D
2
] Interest probability definition. We record how
interest probability is defined and calculated.
[D
3
] Evolution of Interest. We record any possible
discussion that is related to how TD interest
amount grows or shrinks, along evolution. For
example, we capture if a study characterizes in-
terest as compound or simple, or as continuously
increasing.
[D
4
] Interest estimation method. We describe how
TD interest is quantified in the primary study
(when applicable).
The mapping between data extracted and the goals set
in Section 1, are discussed below:
G1: We use [D
1
] and [D
2
]. Based on the frequency of
each variable, we extract the most common def-
initions of interest amount and interest probabil-
ity.
G2: We use [D
3
] that is related to studies, which dis-
cuss the evolution of technical debt interest.
Based on existing literature, and the definitions
derived from G1, we formulate the evolution of
TD interest, and investigate cases when it is in-
creasing or decreasing.
G3: We use [D
4
] that aims at describing how each
study assesses the amount of interest or the in-
terest probability, and synthesize them with the
financial interest theories and the definitions de-
rived from G1, to develop an interest theory that
is applicable for TD.
The outcome of the data collection phase is presented
in Table 1 and Table 2. Specifically, in Table 1, we
present data D
1
and D
2
; whereas in Table 2, we pre-
sent data D
3
and D
4
. We note that due to space limi-
tations: (a) in both tables, the citation is provided with
limited identifiers needed for characterizing a study
(e.g., omitting “et al.”), and (b) in Table 2, we only
present studies that hold a value for at least one vari-
able.
From Table 1, we can observe that about 31% of
primary studies describe interest amount as the extra
effort during maintenance, whereas 51% as the extra
maintenance cost. However, since in software econom-
ics cost is usually defined as a function of effort, we
can assume that 82% of studies refer to interest amount
as the extra effort/cost that is evident during mainte-
nance activities, due to the presence of technical debt.
The rest of the studies, either provide more high-level
definitions – i.e., (Eisenberg, 2012) and (Letouzey,
2012) – or define technical debt interest, similarly to
economics, i.e., the increase rate of technical debt
amount (Ernst, 2012), or define interest as a change in
a design-time quality attribute – see for example (Sea-
man et al., 2012) and (Zazworka et al., 2011). Addi-
tionally, we can observe that approximately 28% of the
studies acknowledge the existence of interest probabil-
ity. From these studies, two – i.e., (Guo and Seaman,
2012) and (Snipes, 2012) – adopt a financial risk man-
agement approach where interest probability is calcu-
lated as the standard deviation of interest rate; whereas
Fifth International Symposium on Business Modeling and Software Design
78

the rest adopt a risk management approach, i.e., they
consider interest probability as the probability of the
TD incurring event to occur.
Table 1: Data Extraction Overview. (1/2).
Study
Interest Amount
Interest Probability
Allman (2012) Increased effort to maintain and extend the
system
Alzaghoul (2013) Cost incurred by time due to an investment at
service level which is not properly managed
Brown (2010) Increased future costs owing to earlier quick
and dirty design and implementation choices
The probability that a particular type
of TD will have visible consequences
Buschman (2011) Cost to be paid later due to quick develop-
ment
Chin (2010) Cost of organization to hold on TD, plus the
additionally incurred debt
Codabux (2013) Additional cost of not eliminating TD now
Curtis (2012,
Software)
Continuing costs attributable to should-fix vi-
olations that haven't been remediated
Curtis (2012,
MTD)
Continuing costs attributable to should-fix vi-
olations that haven't been remediated
Eisenberg (2012) Long-term impact of TD
Ernst (2012) The rate of increase in TD
Falessi (2013) The cost that will occur by not fixing the
technical problem
Interest is not certain. It has a proba-
bility to occur, changing over time
de Groot (2012) The difference in cost between maintenance
at the ideal level and any level below
Guo and Seaman
(2011)
Extra work that will be needed if TD item is
not repaid
Interest standard deviation, because
of the uncertainty of interest
Guo et al. (2011) Additional cost
Holvitie (2013) The amount of extra work the principal can
cause to future development
The probability of extra work TD can
cause to future development
Koolmanojwong
(2013)
More expensive to fix than it is to do it right
the first time
Letouzey (2012) The negative impact of TD
Marinescu (2012) Extra maintenance effort required in the fu-
ture due to hasty, inappropriate design
McGregor (2012) Any extra work over the expected amount,
when later we carry out the deferred activity
Nord (2012) Increasing rework cost of the unpaid TD
Nugroho (2011) The extra maintenance cost spent for not
achieving the ideal quality level
Schmid (2013) Additional effort spent on not quite good code
Seaman (2011) Potential penalty paid in the future as a result
of not completing tasks in the present
The probability that TD, if not repaid,
will make other work more expensive
Seaman (2012) Decreasing maintainability The probability that TD, if not repaid,
will make other work more expensive
Siebra (2012) Extra Effort
Snipes (2012) The extra cost required to complete a mainte-
nance activity in the future if the task is post-
poned, plus the cost of other work that is re-
quired due to the presence of the TD
Interest standard deviation, because
of the uncertainty of interest
Establishing a Framework for Managing Interest in Technical Debt
79

Study
Interest Amount
Interest Probability
Zazworka (2011) Impact on quality
Zazworka (2013) An estimate of the amount of extra work that
will be needed if this TD item is not repaid
The probability that TD, if not repaid,
will make other work more expensive
Zazworka (2014) Probable future cost of not fixing the TD
Table 2: Data Extraction Overview. (2/2).
Study
Interest
Evolution
Estimation Method
Allman (2012) Compound -
Buschman (2011) Compound -
Chin (2010) Both -
Codabux (2013) Increasing -
Guo and Seaman (2011) Expected interest amount and interest standard deviation can be esti-
mated using historical effort, usage, change, and defect data.
Guo et al. (2011) Interest = interest amount × interest probability
IA = X – P,
X: Cost of doing something at t
2
(after postponing at t
1
), P: principal
Nord (2012) Increasing -
Nugroho (2011) interest would be the difference between maintenance effort spent at the
5-star level and any of the lower quality levels
ME = MF*RV/QF
MF=Maintenance Fraction (Historical Data), QF=Quality Factor,
RV=Rebuild Value (estimate of effort to be spent to rebuild a system)
Seaman (2011) Interest amount = W × C, C=average cost of the last N modifications to
module, W=weighting factor , based on the initial rough estimate (high,
medium, or low) of the interest amount
Siebra (2012) Increasing Estimation based on documentation (chronograms, backlogs and code
lines modifications) as the total effort between alternative scenarios
Furthermore, the results of Table 2, suggest that ap-
proximately 21% of primary studies deal with the evo-
lution of interest along time and either characterize it
as compound, or continuously increasing. As an excep-
tion to this, Chin et al. (2010), proposes that one type
of interest is simple. Specifically, they suggest that the
cost of the organization to hold on TD is stable across
time and neither increases nor decreases.
Finally, only 17% of studies propose a specific way
of measuring interest. The estimation is in most of the
cases performed by using historical data, documenta-
tion, and maintenance effort estimation models (for de-
tails see Table 2).
4 FRAMEWORK FOR
MANAGING INTEREST IN TD
In this section we present FItTeD, i.e., the proposed
framework for managing interest in technical debt.
While presenting FItTeD, the discussion focuses on
goals G1 – G3, as set in Section 1. The proposed
framework is based on the findings discussed in Sec-
tion 3 and on the general perception of interest as the
extra effort required for performing any maintenance
tasks when technical debt has been accumulated.
However, it has been enhanced, by our own sugges-
tions to cover gaps in the current literature.
Fifth International Symposium on Business Modeling and Software Design
80

4.1 Types of Interest
From the technical debt literature it is evident that
technical debt interest is perceived as a risk for soft-
ware development, in the sense that it has a specific
effect (i.e., interest amount) and a probability to occur
(i.e., interest probability). Concerning the amount of
interest, we assume that interest can be accumulated
through the extra cost incurred by two activities:
Interest while repaying TD – I(r): The effort for
repaying technical debt at any time point t (i.e.,
enhancing the quality of a Technical Debt Item -
TDI) is higher than the effort needed for repaying
technical debt for this item, at any time point prior
to t. Therefore, I(r) is calculated as the differ-
ence between the two aforementioned efforts.
This type of interest will occur when (and if) the
amount of TD is to be paid off.
Interest while performing maintenance activities
– I(m): Performing maintenance tasks is more
time/effort consuming in parts of the software
with accumulated TD, compared to parts in which
TD is reduced or zero. The difference between the
two amounts of effort is the amount of the I(m)
interest. This type of interest will occur, and will
be simultaneously repaid, when maintenance
tasks are performed (i.e., while undertaking the ef-
fort to perform the maintenance task).
Both the aforementioned types of interest are in
agreement with the most established definitions of in-
terest amount (i.e., extra cost/effort); however by add-
ing more details on when these extra costs/efforts can
occur. Thus, for each technical debt item, interest
(I
TDI
) should be calculated, based on the following
high-level formula:
=
(
)
+
(
)
=
=
(
)
∗
(
)
+
(
)
∗
(
)
,
in which P denotes the probability of a repayment or
maintenance event to occur, E the effort needed to
perform an action, r denotes repayment, and m other
maintenance activities. To transform the aforemen-
tioned formula from the TDI level to the system-level,
we propose the use of the sum aggregation function,
in the sense that the total TD of a system is the sum
of TD, of all items with incurred TD. Therefore, in-
terest at system level (I) can be calculated, as fol-
lows:
=
∗
+
∗
()
We note that the aforementioned formulas cannot
be used per se, but should be instantiated from re-
searchers, by conducting empirical research that
would assign estimates for the P and E factors. For
examples and interesting research directions on this
issue, see Section 5.
4.2 Evolution of Interest
Based on economics, interest is classified over two
dimensions: its method of calculation and its variation
over time. For these purposes, interest can be:
Simple or Compound: Interest is simple when it
is calculated only as a function of the principal;
whereas it is compound when it is calculated over
the principal, plus the incurred interest; and
Fixed or Floating: Interest rate is fixed, if it does
not change along time; whereas it is floating when
it can increase or decrease based on circum-
stances.
Technical debt literature has discussed these charac-
teristics of interest, but only superficially, without em-
pirical evidence on the real-world evolution of inter-
est. As already explained in Section 1, interest rate is
not defined in technical debt. Therefore, the distinc-
tion between floating and fixed interest rates is not ap-
plicable. However, interest amount can still increase
or decrease, based on the amount of debt that it is cal-
culated upon. To this end, we note that studies which
refer to continuously increasing interest are referring
to debt amount and not interest amount.
From observing the literature, we can claim that
researchers perceive technical debt interest as com-
pound, in the sense that it is increasing, since the ad-
ditional effort to repay technical debt and perform
maintenance on a technical debt item increases as soft-
ware grows. At any specific point in time (t
1
), it is
non-trivial to decompose the complexity of the system
to the original system complexity (C
o
), i.e., the one
that existed in the system when the principal incurred,
and the additional system complexity (C
A
), i.e., the
one that incurred due to system evolution (system
larger in size, more functionality, etc.). Therefore, the
calculation of the effort needed to perform any
maintenance action in t
1
, can only be assessed based
on system current complexity (C
c
).
However, interest is not expected to be continu-
ously increasing. We expect that such a claim only
holds for cases when no repayment activities are per-
formed. Specifically, in case that some repayment ac-
tivity is performed (at t
0
), we expect system complex-
ity after partial repayment (C
R
) to decrease (i.e., C
R
<
C
c
), leading to a decreased amount of both types of
interest, in future maintenance activities - E(r|m).
Establishing a Framework for Managing Interest in Technical Debt
81
These claims are valid for individual TDIs, in which
no additional technical debt has been incurred be-
tween timestamps t
0
and t
1
; and
summarized as fol-
lows:
I
Evolution
(
|
)
(
|
)
,
(
)
=0
(
|
)
(
|
)
,
(
)
(
|
)
(
|
)
,
(
)
For example (2
nd
clause): in case the effort spent at
time point t
0
to partially repay technical debt E(r
t
0
)
is lower than the additional interest incurred at t
0
I
t
0
then it is reasonable to assume that any future mainte-
nance or repayment effort E(r|m
t
1
) will be higher
than the corresponding effort required at t
0
E(r|m
t
0
),
in the sense that the amount of debt (diminished de-
sign-time quality or complexity) is larger at t
0
com-
pared to t
1
.
4.3 Interest Theory
Based on the above, and by borrowing the rationale
of the equilibrium achievement from the existing eco-
nomic interest theories, we have been able to develop
an interest theory for managing TD interest. Specifi-
cally, we adopt the concept of the Liquidity Prefer-
ence Theory. The reason for selecting the Liquidity
Preference Theory and not the Loanable Funds The-
ory is that in TD the amount of money that is available
to the company for managing technical debt is stable,
i.e., the amount that has been saved, while incurring
TD – i.e., the principal (supposing that principal is not
invested, to provide extra benefits). The assumption
that the available money for managing TD is princi-
pal, is based on the fact that principal is the maximum
amount that can be spent without spending any addi-
tional effort (other than the one saved).
In the proposed interest theory, we map money
supply to principal, in the sense that principal is the
amount of money that is available to the software de-
velopment company, after incurring TD; and the
money demand to the accumulated amount of inter-
est, in the sense that this is the extra amount of money
that is demanded by the company when perform fu-
ture maintenance activities, caused by the TD. In Fig-
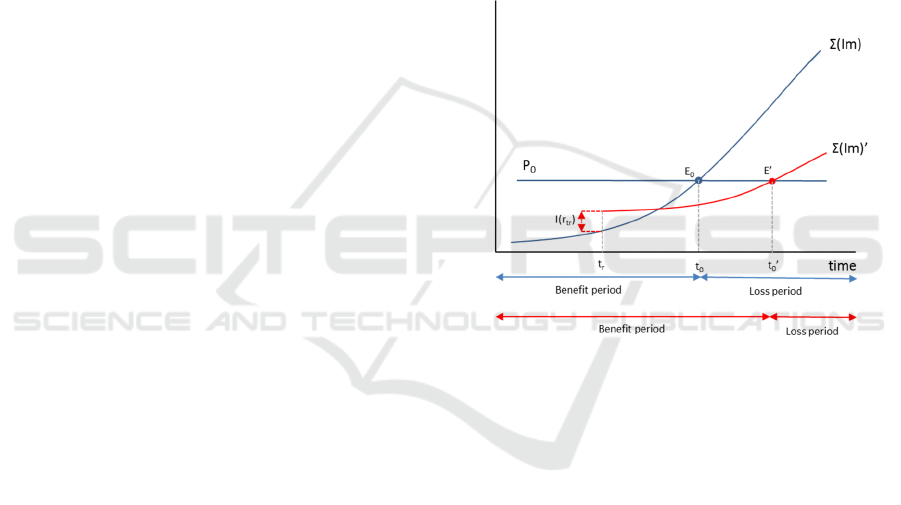
ure 3, where we present the FItTeD Interest Theory,
the x-axis represents time, whereas the y-axis repre-
sents amount of money. Therefore, the equilibrium
point (E
0
) denotes the time stamp (t
0
), in which the
company has spent the complete amount of money
from the internal loan (i.e., initial principal – P
0
) in
extra maintenance activities because of the incurred
TD.
We note that the specification of the equilibrium
point is achieved through an analysis based only on
effort, i.e., the effort saved when taking on TD and
the extra effort required for any future maintenance
activity because of its accumulation. Any other re-
lated costs or benefits related to technical debt occur-
rence (e.g. gains from launching the product earlier)
have been excluded from the model for simplicity
reasons. Thus, if the expected lifespan of the specific
TDI is shorter than t
0
then undertaking technical debt
is a beneficial choice, whereas if not, technical debt
becomes harmful for the company. The aforemen-
tioned discussions, in the case that no repayment ac-
tions are performed, are summarized in the blue lines
of Figure 3.
Figure 3: FItTeD Interest Theory.
Additionally, in Figure 3, we consider Σ(Ιm) as
continuously increasing, since it is a sum of positive
numbers and as exponentially increasing, because TD
interest is compound (see Section 4.2). In case that
some repayment occurs at some timestamp (t
r
), the
line of the accumulated interest Σ(Ιm)is moved up-
wards, due to the interest paid for repayment – i.e.,
I(r
tr
) – but its slope is decreasing, since the interest
is expected to lower for future maintenance activities
(Im). This in turn leads to a shift of the equilibrium
point (E’) to the right, increasing the benefit period
(t
0
’). The fact that principal is lowered to P
tr
(P
tr
<
P
0
), is not presented in the diagram since the money
supply line (P
0
) is not moved, because the originally
available budget of the company is not affected. The
proposed interest theory can help practitioners in their
decision making by:
Identifying the timestamp in which incurring TD,
becomes harmful for the company. Thus, they can
decide if they should undertake the debt.
Fifth International Symposium on Business Modeling and Software Design
82

Supporting them on continuously monitoring the
interest that they have paid so far.
Evaluating the repayment activity, based on the
time-shift of the equilibrium point that it offers.
5 RESEARCH IMPLICATIONS
As already discussed in Section 3 research on TD in-
terest is very theoretical and lacks empirical evidence.
Therefore, in this paper we aim at pointing out spe-
cific research directions, which would boost the em-
pirical research related to TD. The results of these
empirical studies would provide data for the instanti-
ation of the FItTeD interest theory. We organize the
tentative research design by goal:
Types of Interest: An interesting research direction
could be the empirical investigation of:
whether I(r) and I(m) occur with the same fre-
quency, and
whether I(r) and I(m) produce a similar amount
of interest when they occur,
how I(r) and I(m) amount could be modelled, as
a function of the principal, or the underlying struc-
ture of the TDI.
So far, these questions have been explored only by
Guo et al. (2011), Nugroho et al. (2011), and Siebra
et al. (2012), by exploring historical changes and doc-
umentation. The research state-of-the-art lacks real-
world evidence on effort allocation.
Evolution of Interest: A possible empirical investiga-
tion of the evolution of TD interest could reveal inter-
esting characteristics of TD, such as:
What is the relationship of the decay of quality in
the underlying system structure and the increase
in E(m) or E(r)? Answering this question could
guide practitioners on how to model the increase
of interest during software evolution.
How frequently is E(r
t
0
) higher or lower than
I(r
t
0
)? Answering this question could unveil the
frequency with which repayment activities can
constitute interest increasing or decreasing.
FItTeD Interest Theory: In order to increase the ap-
plicability of the proposed TD interest theory, the fol-
lowing questions need to be empirically explored:
What is the average time-shift that is benefited
from performing specific repayment activities?
From what factors is this time-shift influenced?
What is the relationship between I(r) and the av-
erage decrease in the I(m) of future maintenance
activities?
Answering these questions, would enable practition-
ers to instantiate the proposed interest theory, based
on real and context-specific data, and transform FIt-
TeD into a useful tools for practitioners.
6 THREATS TO VALIDITY
In this study, we actually inherit all threats to validity
from the original SLR on which we have based our
results upon (Ampatzoglou et al., 2015):
the identification of primary studies
the generalization of results, and
the conclusions
Concerning data extraction, since we inde-
pendently performed this step, the corresponding
threats are related only to this study. To mitigate bias,
while extracting data, two researchers performed data
collection independently, compared the results and
discussed possible differences. The final dataset was
built through the consent of all authors. Finally, as a
threat we acknowledge that the construction of the
presented formulas, is to some extent based on the un-
derstanding of the authors on TD interest.
7 CONCLUSIONS
Nowadays, Technical Debt (TD) is receiving increas-
ing interest by both academia and practitioners, lead-
ing to an explosion of studies in this field. The cor-
nerstones of TD are two notions borrowed from eco-
nomics: i.e., principal and interest. Although princi-
pal is a well-established term, interest has so far been
discussed in a rather coarse-grained way, with several
contradictions among researchers.
In this paper, we propose FItTeD, i.e., a frame-
work for managing interest in TD, which takes into
account existing TD literature and economic interest
theories. The framework comprise of: (a) a TD inter-
est definition, (b) a classification of TD interest types,
(c) a characterization of TD interest evolution, and (d)
a TD interest theory, based on the Liquidity Prefer-
ence Theory. The proposed framework is expected to
aid in the decision making of practitioners, and points
to interesting research directions. The main emphasis
of the future research directions is on empirical stud-
ies, which until now are underrepresented in the TD
research corpus.
REFERENCES
Allman E., 2012. Managing technical debt. Communica-
tion, 55 (5), pp. 50-55, ACM.
Establishing a Framework for Managing Interest in Technical Debt
83

Alzaghoul E., Bahsoon R., 2013. CloudMTD: Using real
options to manage technical debt in cloud-based service
selection. 4
th
International Workshop on Managing
Technical Debt (MTD ‘13). IEEE Computer Society.
Ampatzoglou A., Ampatzoglou A., Chatzigeorgiou A., Av-
geriou P., 2015. The Financial Aspect of Managing
Technical Debt: A Systematic Literature Review. Infor-
mation and Software Technology, 64, pp. 52-73, Else-
vier.
Brown N., Cai Y., Guo Y., Kazman R., Kim M., Kruchten
P., Lim E., McCormack A., Nord R., Ozkaya I.,
Sangwan R., Seaman C., Sullivan K., Zazworka N.,
2010. Managing technical debt in software-reliant sys-
tems. Proceedings of the FSE/SDP workshop on Future
of software engineering research, pp. 47 – 52, ACM.
Buschmann F., 2011. To Pay or Not to Pay Technical Debt.
Software, 28 (6), pp. 29-31, IEEE Computer Society.
Chin S., Huddleston E., Bodwell W., Gat I., 2010. The Eco-
nomics of Technical Debt, Cutter IT Journal.
Codabux Z., Williams B., 2013. Managing technical debt:
An industrial case study. 4
th
International Workshop on
Managing Technical Debt (MTD ‘13). IEEE Computer
Society.
Cunningham W., 1992. The WyCash Portfolio Manage-
ment System. 7
th
International Conference on Object-
Oriented Programming, Systems, Languages, and Ap-
plications (OOPSLA ’92).
Curtis B., Sappidi J., Szynkarski A., 2012. Estimating the
Principal of an Application's Technical Debt. Software
29 (6), pp. 34 - 42, IEEE Computer Society.
Curtis B., Sappidi J., Szynkarski A., 2012. Estimating the
size cost and types of Technical Debt. 3
rd
International
Workshop on Managing Technical Debt (MTD ‘12).
IEEE Computer Society.
Eisenberg R. J., 2012. A threshold based approach to tech-
nical debt. ACM SIGSOFT Software Engineering
Notes, 37 (2), pp. 1 - 6, ACM.
Ernst N., 2012. On the role of requirements in understand-
ing and managing technical debt. 3
rd
International
Workshop on Managing Technical Debt (MTD ‘12).
IEEE Computer Society.
Falessi D., Shaw M., Shull F., Mullen K., Keymind M.,
2013. Practical considerations challenges and require-
ments of tool-support for managing technical debt. 4
th
International Workshop on Managing Technical Debt
(MTD ‘13). IEEE Computer Society.
de Groot J., Nugroho A., Back T., Visser J., 2012. What is
the value of your software?, 3
rd
International Workshop
on Managing Technical Debt (MTD ‘12). IEEE Com-
puter Society.
Guo Y., Seaman C., 2011. A portfolio approach to technical
debt management. 2
nd
International Workshop on Man-
aging Technical Debt. ACM.
Guo Y., Seaman C., Gomes R., Cavalcanti A., Tonin G., da
Silva F., Santos A.L., Siebra C., 2011. Tracking tech-
nical debt - An exploratory case study. 27
th
Interna-
tional Conference on Software Maintenance (ICSM
‘11). IEEE Computer Society.
Holvitie J., Leppanen V., 2013. DebtFlag: Technical debt
management with a development environment inte-
grated tool. 4
th
International Workshop on Managing
Technical Debt (MTD ‘13). IEEE Computer Society.
Kitchenham B., Brereton O. P., Budgen D., Turner M., Bai-
ley J., Linkman S., 2009. Systematic literature reviews
in software engineering – A systematic literature re-
view. Information and Software Technology, 51 (1), pp
7-15. Elsevier.
Koolmanojwongand S., Lane J.A., 2013. Enablers and In-
hibitors of Expediting Systems Engineering. 11
th
An-
nual Conference on Systems Engineering Research
(CSER ‘13). Procedia Computer Science, Elsevier.
Li Z., Avgeriou P., Liang P., 2015. A systematic mapping
study on technical debt and its management. Journal of
Systems and Software, 101, pp. 193-220. Elsevier.
Letouzey J. L., 2012. The sqale method for evaluating tech-
nical debt. 3
rd
International Workshop on Managing
Technical Debt (MTD ‘12). IEEE Computer Society.
Marinescu R., 2012. Assessing technical debt by identify-
ing design flaws in software systems. Journal of Re-
search and Development, 56 (5), pp. 1-13, IBM.
McGregor J. D., Monteith J., Zhang J., 2012. Technical
debt aggregation in ecosystems. 3
rd
International Work-
shop on Managing Technical Debt (MTD ‘12). IEEE
Computer Society.
Mishkin F., Eakins S., 2012. Financial Markets and Insti-
tutions. Pearson Prentice Hall, 7
th
Edition.
Nord R., Ozkaya I., Kruchten P., Gonzalez-Rojas M., 2012.
In Search of a Metric for Managing Architectural Tech-
nical Debt. 2012 Joint Working IEEE/IFIP Conference
on Software Architecture (WICSA) and European Con-
ference on Software Architecture (ECSA). IEEE Com-
puter Society.
Nugroho A., Visser J., Kuipers T., 2011. An empirical
model of technical debt and interest. 2nd International
Workshop on Managing Technical Debt (MTD’ 11).
ACM.
Schmid K., 2013. On the limits of the technical debt meta-
phor some guidance on going beyond. 4
th
International
Workshop on Managing Technical Debt (MTD ‘13).
IEEE Computer Society.
Seaman C., Guo Y., 2011. Measuring and monitoring tech-
nical debt. Advances in Computers, 82, pp. 25-46. Else-
vier.
Seaman C., Guo Y., Zazworka N., Shull F., Izurieta C., Cai
Y., Vetro A., 2012. Using technical debt data in deci-
sion making: Potential decision approaches. 3rd Inter-
national Workshop on Managing Technical Debt
(MTD’ 12). IEEE Computer Society.
Siebra C. S., Tonin G. S., Silva F. Q., Oliveira R. G., Junior
A. L., Miranda R. C., Santos A. L., 2012. Managing
technical debt in practice: an industrial report. 6th In-
ternational Symposium on Empirical Software Engi-
neering and Measurement (ESEM’ 12). ACM.
Snipes W., Robinson B., Guo Y., Seaman C., 2012. Defin-
ing the decision factors for managing defects: A tech-
nical debt perspective. 3rd International Workshop on
Managing Technical Debt (MTD’ 12). IEEE Computer
Society.
Fifth International Symposium on Business Modeling and Software Design
84

Zazworka N., Seaman C., Shull F., 2011. Prioritizing de-
sign debt investment opportunities. 2
nd
International
Workshop on Managing Technical Debt (MTD’ 11).
ACM.
Zazworka N., Spanola R. O., Vetró A., Shull F. Seaman
C., 2013. A case study on effectively identifying tech-
nical debt. 17
th
International Conference on Evaluation
and Assessment in Software Engineering. ACM.
Zazworka N., Vetró A., Izurieta C., Wong S., Cai Y., Sea-
man C. Shull F., 2014. Comparing four approaches for
technical debt identification. Software Quality Journal.
22 (3), pp. 403 – 426, Springer.
Establishing a Framework for Managing Interest in Technical Debt
85
