
Towards Lock-Free Distributed Transactions
Rustem Kamun, Askhat Omarov, Timur Umarov
Department of Information Systems Management, Kazakh-British Technical University, 59, Tole bi str., Almaty, Kazakhstan
{r.kamun, askhat.omarov91}@gmail.com, t.umarov@kbtu.kz
Sanzhar Altayev
sanzhar@altayev.kz
Keywords:
Clock synchronization, timestamp, Marzullo’s algorithm, distributed systems, cluster, node, TrueTime, HLC.
Abstract:
For the last 40 years storage systems evolved greatly from traditional relational databases to distributed storage
systems. Such dramatic changes are caused by exponential growth of Internet and mostly defined by its users
and services (Int, 2014). For the past recent years both industrial and academic projects have recognized the
necessity for strong consistency and ACID transactional semantics in large distributed storage systems. The
main objective of this paper is to provide such strong consistency in the manner of Googles TrueTime described
in (Corbett et al., 2013). We address the limitations of Google Spanner for general-purpose transactions. The
result of this paper is a clock synchronization protocol (CSP) for transactions at scale.
1 INTRODUCTION
According to the CAP theorem (Gilbert, 2012), pre-
sented by professor Eric Brewer any system that re-
lies on persistence layer is characterized by a subset
of the following properties: data consistency, system
availability and tolerance to network partition. How-
ever, distributed systems undergo network partitions
which results in impossibility to gain both consistency
and availability in distributed storage systems. For
the recent years, pressures caused by rapidly grow-
ing number of users and data sets have driven system
designs away from conventional centralized RDBMs
(supporting joins and relational schemes) and toward
more scalable distributed solutions, including simple
key-value storage systems, as well as more elaborate
NewSQL databases that support transactions at scale.
Ideally, a transactional system provides serial-
izability. However, serializability comes with low
concurrency and high network overheads. Hence,
commercial storage systems use a weaker guarantee,
snapshot isolation, since it allows for high concur-
rency between transactions as well as data replication
and partitioning (David Bermbach, 2013).
It is straightforward how to supply data snapshot
at some point in time on a single node. One solu-
tion is to mark each mutation operation with current
wall time on this node. However, choosing a times-
tamp for transaction executed over multiple nodes is
challenge due to clock rate, drift and jitter on each
involved node (Mills, 1995; Moon et al., 1999). For
this reason there exists clock-based algorithms to or-
der events (ordering transactions, operations and etc.)
in distributed services (Marzullo and Owicki, 1983;
Lamport, 1978). For example, Amazon Dynamo (Vo-
gels, 2009) uses Vector Clocks (VC) to track causal-
ity of mutations to the replicas. Cassandra (Laksh-
man and Malik, 2010) uses Physical Time and Last-
Write-Wins rule on column granularity level to retain
consistency during state transition. But both Cassan-
dra and Dynamo sacrifice strong ACID semantics to
fault-tolerance and scalability. Google Spanner (Cor-
bett et al., 2013) employs True Time (TT) to provide
global ordering between any two non-overlapping
transactions. However, TT is built upon special time
references (GPS, atomic clocks), wait intervals and
high enough bandwidth and speed to guarantee neg-
ligible latencies within Google, while we deal with
unpredictable network conditions where data transfer
rates and physical characteristics of connections vary
widely. Using NTP instead of TT with wait inter-
vals in such systems causes several hundred of mil-
liseconds latencies between transactions. In a con-
tended system with long-running transactions (OLTP)
247
Kamun R., Omarov A., Umarov T. and Altayev S.
Towards Lock-Free Distributed Transactions.
DOI: 10.5220/0005887802470252
In Proceedings of the Fifth International Symposium on Business Modeling and Software Design (BMSD 2015), pages 247-252
ISBN: 978-989-758-111-3
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and high traffic load, throughput and in turn response
rate can decrease significantly. Therefore wait inter-
vals are inappropriate since it may lead to denial of
service.
The main result of this paper is a clock synchro-
nization protocol (CSP) for general-purpose transac-
tions at scale. In designing CSP we employed hybrid
logical clock (HLC) that leverages the best of logical
clocks and physical clocks. HLC is helpful for track-
ing causality relationship of the overlapping events.
CSP is generalized and can meet the needs of any
practical system and its efficiency is comparable to
NTP and Google TT.
The rest of the paper is organized as follows. In
Section 2 we analyze different synchronization meth-
ods emerged for the last forty years, provide the basic
notations used throughout the paper and analyze the
core of clock synchronisation algorithm. In Section
3 we present the core algorithms CSP is based upon.
Then, in Section 4 we provide briefly implementation
details and show the results of toy example. We con-
clude the paper in Section 5.
2 RELATED WORK
The problem of consistency in distributed systems is
tightly related to the synchronization problem. Syn-
chronization of the nodes implies deterministic or-
der of distributed transactions which in turn ensures
safety (data consistency and integrity).
In 1978 Lamport proposed a way to order events
based on logical clocks (Lamport clocks or LC)
(Lamport, 1978). The key property that have to be
satisfied by logical clocks is ”happened before“ con-
dition: for any two events i, j in the system, if i ”hap-
pend before“ j then C(i) < C( j). Based on this condi-
tion, timestamp assignment described by the two fol-
lowing rules:
• If event j happened locally at some node P after
event i, then C( j) = C(i) + 1;
• If some process Q sends message m to process
P, then it piggybacks m with a timestamp T
m
that
equals to latest clock(Q)+1. Upon receiving this
message (defined as event j), process P assigns a
timestamp that must be greater or equal to its cur-
rent value and strictly greater than T m.
However LCs are impractical in distributed storage
systems for the following reasons:
• It is not possible to query events with respect to
physical time.
• LCs do not consider external events to be a part of
their event sets (no back-channels).
Ten years later the vector clock (VC) was pro-
posed by (Fidge, 1988) to extract more knowledge
about communication behaviour in the system. Deal-
ing with VC, each node maintains a vector that col-
lects the knowledge this node possesses about the log-
ical clocks of all other nodes. VC finds all possible
consistent snapshots, which is useful for debugging
applications. However since the number of sites in
a popular distributed system can be on the order of
thousands, maintenance of the causality information
using VC is highly prohibitive because space require-
ment is in the order of nodes in the system.
Network Time Protocol (NTP) presented by D.
Mills at (Mills, 1995) synchronizes computer physical
clock with sources known to be synchronized: dedi-
cated time servers, radio and satellite receivers, etc.
NTP avoids the disadvantages of LC, however, it pro-
vides tens of milliseconds accuracies on WANs which
entails an inability of tracking causality of events
that has occurred at overlapping uncertainty regions.
Moreover, NTP is not accurate due to not stable net-
work conditions (asymmetric routes and congestion)
and problems such as leap seconds (Allen, 2015).
TrueTime (TT) was proposed by Google in (Cor-
bett et al., 2013), a multiversion, geographically dis-
tributed database. Spanner discards the tracking of
causality information completely. Instead, it uses
highly-precise external clock sources to reduce the
size of the uncertainty intervals to be negligible and
order events using wall-clock time. Such ordering in
TT is stronger than the causal happened-before rela-
tion in traditional distributed system since it does not
require any communication to take place between the
two events to be ordered; sufficient progression of the
wallclock between the two events is enough for or-
dering them. TT enables lock-free reads in Spanner;
it provides simple snapshot reads by just giving a time
in the past. Snapshot reads is not an easy task to ac-
complish in a distributed system without using TT.
This would require capturing and recording causality
between different versions of variables using VC, so
that a consistent cut can be identified for all the vari-
ables requested in the snapshot read. However using
VC is infeasible as we discussed previously.
When the uncertainty intervals are overlapping,
TT cannot order events and that is why in order to en-
sure sufficient progression of the wallclock between
these events it has to explicitly wait advertised uncer-
tainty interval. Moreover this approach requires ac-
cess to specialized hardware (GPS and atomic clocks)
to maintain tightly synchronized time at each node.
These limitations causes Google approach to be in-
appropriate for general-purpose transactions where
the waits on uncertainty bounds can significantly de-
Fifth International Symposium on Business Modeling and Software Design
248
crease the concurrency and in turn system availability.
Given the importance of transactions in large-scale
software systems, we decided to design an alterna-
tive clock synchronization protocol with more viable
properties for general-purpose than Google Spanner.
Kulkarni et al. (Kulkarni et al., 2014) introduced
a Hybrid Logical Clock (HLC) algorithm that avoids
all disadvantages mentioned in TT, LC and NTP. HLC
leverages both LC and PT. The HLC timestamp is
within 64-bit of NTP timestamp. When the uncer-
tainty intervals of two events are overlapping, the LC
part of HLC tracks the causality between these events.
3 DESIGN OF CSP
Before we dive into algorithm details CSP is
based upon, it is important to understand termi-
nology and notations used throughout the paper.
pt(n) is a current wall time at node n. l(n) is a largest
wall clock time among all events occurred so far at
node n. c(n) is logical part of HLC that tracks causal-
ity between two events when their l parts are equal at
node n. When message m is sent to node n, it pig-
gybacks with < l(m), c(m) > by some server i. ε is
a heuristic parameter that defines how far ahead of
physical clock the wall time can be or simpler, it de-
fines an upper/lower bound for offset on a single node.
hlc(n) is a hybrid logical clock or a more verbose ver-
sion is represented by a pair (l(n), c(n)).
3.1 HLC Timestamping
There are two types of event handled by HLC algo-
rithm: send(local), receive. Figure 2 outlines an HLC
algorithm. Initially, l and c parts are set to 0. When
a new send event f is created at node n, l(n) is set to
max(l
0
(n), pt(n)), where l
0
(n) is a previous assigned
value or 0. However, it is still possible that l(n) is
equal to l
0
(n) and if that is the case then we increment
its logical part, c(n), by 1. Otherwise, set c(n) part to
0. If at any point in time, receive event f is occurred
at node n, l(n) is equal to max(l(n), l(m), pt(n)). If
pt(n) is greater than both, l(n) and l(m), then set (n)
to 0 and return a pair < l(n), c(n) >. Otherwise, c(n)
is set depending on whether l(n) equals to l(e), l(m),
or both. By incrementing c parts in the just men-
tioned cases, HLC provides important invariant: for
any two subsequent events, e and f , occurred at some
node n if e occurred before f , then hlc
e
(n) < hlc
f
(n)
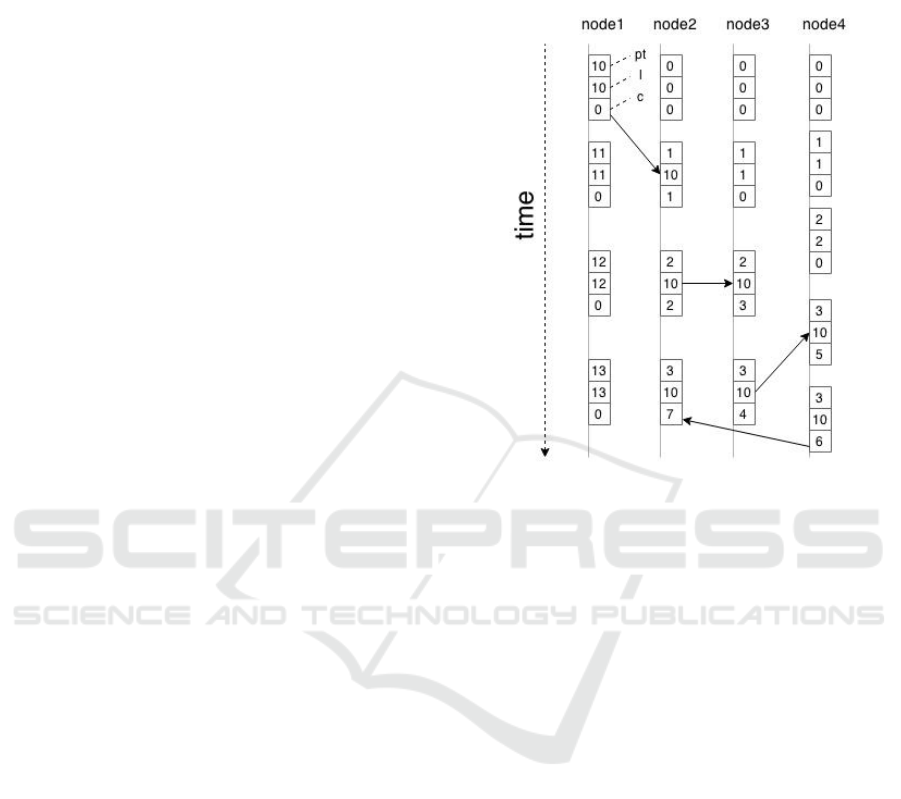
(Kulkarni et al., 2014). Figure 1 depicts how algo-
rithm works on a “space-time” diagram. The horizon-
tal direction represents space. The vertical direction is
time with earlier times being higher than later times.
Each box represents an event marked by hlc times-
tamp. The vertical lines denote nodes, and the arrows
denote messages between them.
Figure 1: Space-Time diagram of HLC algorithm.
The major benefit of HLC is its agnosticism to
network conditions and to architecture of distributed
system. Instead of tweaking the node’s local clock,
HLC only reads it and updates l and c parts accord-
ingly. Although HLC leverages NTP for synchroniza-
tion, it can use any other clock synchronization algo-
rithm/protocol.
Kulkarni et al. (Kulkarni et al., 2014) advice to
set ε to sufficiently large value depending on applica-
tion constraints in order to be resilient to clock syn-
chronization errors. But it would be abnormally large
space for (l − pt) offset in case of distributed transac-
tional storage system. It can significantly increase the
number of aborted/restarted transactions in the sys-
tem and decrease the concurrency level proportion-
ally. Hence, we decided to maintain maximum off-
set, ε, at each involved node within several hundred
of milliseconds for NTP in the manner of Google
Spanner (Corbett et al., 2013) (the ε can be improved
further, if the network conditions are more optimistic
(e.g. geographically-proximate clusters)).
3.2 Offset Maintenance
Offset maintenance is implemented at each involved
node in the cluster. Each node in the cluster main-
tains the list of remote clocks. Remote clock is a lo-
cal clock of any node in the cluster (wallclock) except
Towards Lock-Free Distributed Transactions
249

1: function SENDTS
2: if l(n) ≥ pt(n) then
3: c(n) ← c(n) + 1
4: else
5: l(n) ← pt(n)
6: c(n) ← 0
7: end if
8: return < l(n), c(n) >
9: end function
Send or local event
1: function RECEIVETS
2: if pt(n) > l(n) & pt(n) > l(m) then
3: l(n) ← pt(n)
4: c(n) ← 0
5: return < l(n), c(n) >
6: end if
7: if l(m) > l(n) then
8: l(n) ← l(m)
9: c(n) ← c(n) + 1
10: else if l(n) > l(m) then
11: c(n) ← c(n) + 1
12: else
13: if c(m) > c(n) then
14: c(n) ← c(m)
15: end if
16: c(n) ← c(n) + 1
17: end if
18: return < l(n), c(n) >
19: end function
Receive event of message m
Figure 2: HLC algorithm
for the maintainer node. It is easy to understand the
key parts of the algorithm by an example. Assume a
cluster with three nodes: 1, 2 and 3. Then node 1 will
maintain a list of remote clocks [HLC(2), HLC(3)].
To maintain a single remote clock of node i, node
j periodically polls it. During each such round-trip,
node j applies a version of Cristian’s algorithm (Iwan-
icki et al., 2006; Cristian and Fetzer, 1994) to estimate
node’s i clock as depicted at Figure 3.
Figure 3: Christian algorithm.
Later, the node j records an HLC timestamp T
1
( j)
and sends a heartbeat message to node i. After re-
ception of this message, i records timestamp T
2
(i) ac-
cording to its local clock and starts to prepare a re-
sponse message containing the recorded timestamp.
When the message is ready, i records timestamp T
3
(i),
piggybacks a pair < T
2
(i), T
3
(i) > within a response
message and sends it back to j . As soon as the mes-
sage is delivered, j records timestamp T
4
( j) accord-
ing to its local clock. At this point, node j has the
following set of timestamps: T
1
( j), T
2
(i), T
3
(i), T
4
( j)
(called a synchronization sample). Since the propaga-
tion delays from i to j and from j to i are comparable,
the sample allows j to estimate the round-trip delay
(eq.(1)), the offset of i. (eq.(2)) and clock reading er-
ror (eq.(3)):
σ = T
4
( j) − T
1
( j) − (T
3
(i) − T
2
(i)) (1)
θ = T
3
(i) +
σ
2
− T
4
( j) (2)
ξ =
σ
2
(3)
Finally, node j updates information about node i’s off-
set, error and the time of measurement.
Periodically (multiple of heartbeat interval) node j
uses the list of remote clocks C(i) (where i ∈ [1, N] ∧
i 6= j) and applies Marzullo’s intersection algorithm
(Marzullo and Owicki, 1983) to estimate a “true” off-
set using N −1 sources. The outcome of algorithm de-
pends on an important property – majority of sources.
So, for N −1 sources, the offset is considered “true” if
and only if
N−1
2
+1 sources are intersected at it. If the
estimated offset is greater than allowed ε then node
j is evicted. Thereby the system is protected against
nodes with broken clocks. It implies that at any node
in the system clock uncertainty is maintained within
[−ε, +ε] bounds.
4 IMPLEMENTATION OF CSP
Current implementation of CSP is built on the follow-
ing technology stack
1
:
• Application layer is built using python gevent
2
.
• Lightweight persistence layer is based on etcd
3
.
The algorithms and methods mentioned in Section
2 involve tight interaction between nodes in the clus-
ter. To facilitate a proper interaction of nodes and ex-
ecution of CSP in overall, we implemented/used the
following protocol stack: 1) ”All-to-all“ heartbeating
2) ”Liar’s suicide“ protocol 3) HLC 4) NTP. Further
we discuss the key role of yet to be mentioned pro-
tocols. At the end of this section we describe the toy
example that exemplifies implemented CSP.
4.1 ”All-To-All“ Heartbeating
As soon as node joins the cluster it starts maintaining
membership changes (joins, drop-outs and failures)
and clock of every other node in the cluster by ex-
changing RPC messages. The general workflow looks
as follows:
1. Every cluster member periodically transmits a
”heartbeat“ message to all other group members.
1
source code could be obtained at github repository
available by https://github.com/Rustem/tt.
2
A coroutine-based Python networking library that uses
lightweight pseudo threads to provide a high-level syn-
chronous API on top of the event loop.
3
A distributed consistent key value store
Fifth International Symposium on Business Modeling and Software Design
250

2. Every node i is considered failed by a non-faulty
member j when node j does not receive heartbeats
from i for certain time period T
heartbeat
.
3. Every node, received a ”heartbeat“ request, re-
sponses with a message piggybacked with T
2
(i)
and T
3
(i) (receive and send timestamps) that are
further used to estimate clock offset.
The heartbeat request and response message structure
is depicted in Figure 4.
message HeartbeatRequest {
optional string ping = 1;
optional int64 counter = 2;
}
message HeartbeatResponse {
optional string pong = 1;
optional int64 counter = 2;
optional int64 recv_time = 3;
optional int64 send_time = 4;
}
Figure 4: Heartbeat protocol
4.2 ”Liar’s Suicide“ Protocol
A liar is the node that has a broken local clock. Clock
is considered broken if it exhibits frequency excur-
sions larger than the worst-case bound. Such nodes
must be evicted from the system to maintain an ad-
vertised ε. To distinguish such nodes, we propose an
algorithm (similar to Spanner) that is based on clock
offset maintenance. Clock offset denotes how far one
clock ahead of other clock. Single offset message
about some node has structure as depicted at Figure
5.
message RemoteOffset {
optional int64 offset = 1;
optional int64 error = 2;
optional int64 measured_at = 3;
}
Figure 5: Offset protocol
Each node maintains a list of remote clock offsets.
Every T
monitor
interval (equal to c ∗ T
heartbeat
, where c
is a positive constant) is an each member of a cluster
applies Marzullo’s algorithm on that list to estimate
its current ”true“ offset interval. If the interval is ei-
ther not shared by the majority of the references or out
of uncertainty bounds, then the node is considered as
a liar, which in turn causes it to suicide.
4.3 Toy Example
The main goal of an example application is to demon-
strate the distribution of logical clock value under
massive loads. The example application could be
summarized as follows: each node generates local
events as well as sends messages to other nodes with
the same predefined rate. Each received event (mes-
sage) is assigned with HLC timestamp and stored in
the database. Example application has the follow-
ing environment: there are three nodes in the system
hosted at different racks in Amsterdam. As hosting
provider we have chosen Digital Ocean
4
. One of the
nodes is master node. Each node has the following
characteristics:
• Hardware: 4GB of RAM, 60GB SSD Disk, 2xIn-
tel Hex-Core CPUs
• Software: Ubuntu 14.04 OS, Python 2.7.6. Each
node is configured with NTP stratum 2. Master
node is equipped with database PostgreSQL and
configuration in-memory storage, etcd.
This example has tested under different event rates:
a) 100 messages per second as shown at figure 6
b) 1000 messages per second as shown at figure 7.
For the first case, the maximum logical value is 3.
98% comprised logical value of 0 and 1. The over-
all offset was between 5-10 ms. For the second case,
the maximum logical value is 23. 60% of the total
comprised logical value range 0-7. The overall offset
was between 16-20 ms
5
.
Figure 6: Distribution of logical value (100 msgs/sec).
5 CONCLUSION
In this paper, we introduced the clock synchroniza-
tion algorithm (CSP) that combines the benefits of
both physical and logical clocks. CSP uses HLC
4
https://www.digitalocean.com/
5
Statistics has built on a dataset with more than 50 000
messages
Towards Lock-Free Distributed Transactions
251

Figure 7: Distribution of logical value (1000 msgs/sec).
for timestamping and therefore it is viable for arbi-
trary distributed architecture. According to the bench-
marks presented in (Kulkarni et al., 2014), deployed
in WAN, even in the presence of straggler nodes and
high event rate, the logical part, c, of HLC was no
higher than 1000 (though only at the struggle node).
In addition, HLC is backward compatible with TT
and LC. When ε is infinity, CSP behaves more like
an LC used for causality tracking in asynchronous
distributed systems. When ε is small, CSP behaves
more similar to Google TT. In the manner of Google
Spanner, we have leveraged the stack of distributed
protocols/algorithms to keep clock offset at any node
within advertised bounds. In turn it ensures another
level of CSP resiliency to different types of errors.
A snapshot read with our implementation is simi-
lar to TT-based Spanner. For a snapshot read of data
items x and y at absolute time t, the client executes the
reads at nodes i, j that are hosting x and y and that are
sufficiently up to date (updated to at least t − ε). Let
t
x
(respectively t
y
) denote the timestamp of the latest
update to x (resp. y) before t −ε at i (resp. j). Reading
the values of x at t
x
and y at t
y
gives a consistent snap-
shot because at time t the values of x and y are still
the same as those at t
x
and t
y
by definition of t
x
and
t
y
. However, if say x has another update with times-
tamp t
0
x
within the uncertainty interval of t
x
then we
use HLC comparison to order those two to identify
the latest version to return from i.
CSP can provide a slightly relaxed version of
the external-consistency guarantee in TT-based im-
plementation of Spanner. In case, when a transaction
T 1 commits (in absolute time) before another transac-
tion T 2 starts, it is still possible to have an overlap be-
tween the uncertainty intervals of T 1 and T 2. In case
T 1 and T 2 are causally-related then CSP will still give
the same guarantee as TT because T 2’s assigned HLC
timestamp will be bigger than T 1’s. Otherwise, CSP
will give a slightly relaxed guarantee and will only en-
sure that T 2’s assigned HLC commit timestamp will
not be smaller than T 1’s.
In nearby future, our main objective is to bring
general-purpose transactional protocol with CSP at its
core to Open-Source.
REFERENCES
(2014). Internet growth statistics. http://www.
internetworldstats.com/emarketing.htm. Ac-
cessed: 2015-03-30.
Allen, S. (2015). The future of leap seconds. http://www.
ucolick.org/
˜
sla/leapsecs/onlinebib.html.
Accessed: 2015-02-20.
Corbett, J. C., Dean, J., and Epstein, M. (2013). Spanner:
Googles globally distributed database. ACM Transac-
tions on Computer Systems, 31.
Cristian, F. and Fetzer, C. (1994). Probabilistic internal
clock synchronization. In Reliable Distributed Sys-
tems, 1994. Proceedings., 13th Symposium on, pages
22–31.
David Bermbach, J. K. (2013). Consistency in distributed
storage systems: An overview of models, metrics and
measurement approaches. In Proceedings of the Inter-
national Conference on Networked Systems (NETYS).
Fidge, C. (1988). Timestamps in message-passing sys-
tems that preserve the partial ordering. In Proceedings
of the 11th Australian Computer Science Conference
02/1988, pages 10:56–66.
Gilbert, S. (2012). Perspectives on the cap theorem. Com-
puter, 45:30–36.
Iwanicki, K., van Steen, M., and Voulgaris, S. (2006).
Gossip-based clock synchronization for large decen-
tralized systems. In Self-Managed Networks, Systems,
and Services. Second IEEE International Workshop,
SelfMan 2006, Dublin, Ireland, June 16, 2006. Pro-
ceedings, volume 3996, pages 28–42.
Kulkarni, S. S., Demirbas, M., Madeppa, D., Avva, B., and
Leone, M. (2014). Logical physical clocks and consis-
tent snapshots in globally distributed databases. In The
18th International Conference on Principles of Dis-
tributed Systems.
Lakshman, A. and Malik, P. (2010). Cassandra: a decen-
tralized structured storage system. ACM SIGOPS Op-
erating Systems Review, 44:35–40.
Lamport, L. (1978). Time, clocks, and the ordering of
events in a distributed system. Communications of the
ACM, 21:558–565.
Marzullo, K. and Owicki, S. (1983). Maintaining the time
in a distributed system. In PODC ’83 Proceedings of
the second annual ACM symposium on Principles of
distributed computing, pages 295–305.
Mills, D. L. (1995). Improved algorithms for synchronizing
computer network clocks. IEEE/ACM Transactions
on Networking (TON), 3:245–254.
Moon, S., Skelly, P., and Towsley, D. (1999). Estima-
tion and removal of clock skew from network delay
measurements. In INFOCOM ’99. Eighteenth Annual
Joint Conference of the IEEE Computer and Commu-
nications Societies. Proceedings. IEEE, volume 1.
Vogels, W. (2009). Eventually consistent. Communications
of the ACM - Rural engineering development, 52:40–
44.
Fifth International Symposium on Business Modeling and Software Design
252
