InterCriteria Software Design: Graphic Interpretation

within the Intuitionistic Fuzzy Triangle

Deyan Mavrov

, Irina Radeva

, Krassimir Atanassov

, Lyubka Doukovska

and Ivan Kalaykov

Prof. Dr. Asen Zlatarov University

1 Prof. Yakimov Blvd., 8010 Burgas, Bulgaria

dg@mavrov.eu

Institute of Information and Communication Technologies, Bulgarian Academy of Sciences

Acad. G. Bonchev str., bl. 2, 1113 Sofia, Bulgaria

iradeva@iit.bas.bg, doukovska@iit.bas.bg

Institute of Biophysics and Biomedical Engineering, Bulgarian Academy of Sciences

Acad. G. Bonchev str., bl. 105, 1113 Sofia, Bulgaria

krat@bas.bg

Örebro University, School of Science and Technology

SE-701 82 Örebro, Sweden

ivan.kalaykov@oru.se

Keywords: InterCriteria Analysis, Software design, Software implementation, Intuitionistic fuzzy sets, Index matrix.

Abstract: The InterCriteria Analysis (ICA) method offers an interesting new way for pairwise comparison of criteria

among a set of criteria, against which a set of objects have been evaluated. This has been designed as a

completely data driven method, which requires real data to practically see effect of its application.

A specialized software application has been developed, which requires as input one two-dimensional array

of data of the evaluation of the set of m objects against the set of n criteria, and after processing returns as

output two n×n tables, the first of which contains the membership parts, and the second – the non-

membership parts of the intuitionistic fuzzy pairs that define the degrees of correlation between any two

criteria in the set of criteria. Having presented the implementation of the basic ICA algorithm in (Mavrov,

2015), we present here a recently developed additional feature for graphical interpretation of the results of

ICA, plotted as points in the Intuitionistic Fuzzy Interpretational Triangle, which reflects in the software

application the new theoretical developments of the ICA approach, as discussed in (Atanassova, 2015).

1 INTRODUCTION

The novel InterCriteria Analysis (ICA) method was

proposed in (Atanassov, et al, 2014) and

significantly developed in a series of publications,

including (Atanassova, et al, 2014a, 2014b, 2014c),

(Atanassova, 2014) and others in (InterCriteria

Research Portal, 2015).

Along with its theoretical development and

search of testing datasets for approbation and app-

lication of the approach, intensive work has started

on the software implementation of the ICA. In

(Atanassova, 2015) the basic algorithm’s implem-

entation has been presented, and here we continue

with presentation of a new phase of development of

the ICA software, using functionalities for graphic

output and human-machine interaction with the ICA

results.

The ICA offers an interesting new way for

comparison of the individual criteria among a set of

criteria, against which a set of objects have been

evaluated. This has been designed as a completely

data driven method, which requires real data to

practically see effect of its application. The algo-

rithm, and the software application, require as input

one two-dimensional array of data of the

279

Mavrov D., Radeva I., T. Atanassov K., Doukovska L. and Kalaykov I.

InterCriteria Software Design - Graphic Interpretation within the Intuitionistic Fuzzy Triangle.

DOI: 10.5220/0005888202790283

In Proceedings of the Fifth International Symposium on Business Modeling and Software Design (BMSD 2015), pages 279-283

ISBN: 978-989-758-111-3

evaluations, or measuring, of a set of m objects

against a set of n criteria. As a result of application

of the algorithm, we expect a new table, n×n, which

contains intuitionistic fuzzy pairs that define for

each pair of criteria the degree of membership and

non-membership of the IF correlation between the

two criteria in the pair of criteria. In our implement-

ation, for the needs of more handy operation, the

result is returned in the form of two output n×n

tables, the first of which contains only the member-

ship parts, and the second one – only the non-

membership parts of these Intuitionistic fuzzy pairs.

2 LANGUAGE AND LIBRARIES

For reader’s convenience, here we will again, after

(Mavrov, 2015), present the basic prerequisites for

the software application: the programming language

and the libraries that have been employed in the

process of development.

The application is developed using the C++ pro-

gramming language. The development environment

is Microsoft Windows. For compiler, the standard

programme CL.exe from the Visual C++ 2012 has

been used, without using the Visual Studio graphic

environment.

Based on previous experience, the Qt library was

chosen for the application’s graphical interface. Qt

offers classes, which help building the on-screen

graphic objects, as well as classes for non-graphic

objects like (strings, database connections, etc.).

Each Qt class object can interact with the rest

objects, using a system of signals and slots, and

sending a signal from one object can be connected to

another object’s slot. The Qt library is cross-

platform library, which works with a variety of

operating systems and compilers, and in case that

only the standard Qt classes are used, an application

designed under Windows, can get compiled under

Linux with almost no changes. Moreover, the Qt

project includes a C++ program development

environment, Qt Creator. It offers a visual editor for

design of windows, which significantly facilitates

the use of the graphic interface.

The remaining important details of the basic

software implementation, like format of the input

data, the design of the main module of the program,

basic functionalities like reading of the input data,

processing of these data and calculation of the IF

values, as well as the output of the result, have been

discussed in details in (Mavrov, 2015) and will not

be repeated here.

3 MODULE FOR ICA RESULTS’

GRAPHIC VISUALIZATION

The Qt library allows working with two dimensional

graphics, by using the classes QGraphicsView

and QGraphicsScene. They allow on screen

visualization of various forms and shapes, using

lines, circles and other objects. For this aim, in a

new class for window, called IFS_Triangle, an

object from the new class IFS_GraphicsView is

being imported, which inherits QGraphicsView.

Creating own inheriting class for the graphic

window, allows higher flexibility in drawing the

objects. The graphic window opens after clicking on

the ‘Graphic’ button.

The visualization of the results obtained after

applying the ICA algorithm over input data, requires

us to use the intuitionistic fuzzy triangle, see

(Atanassov, 1989), (Atanassov, 1999), (Atanassov,

2012). It is a triangle from the Euclidean place, with

vertices (0, 0), (1, 0) and (0, 1), where the

intuitionistic fuzzy membership part μ is plotted

along the abscissa, and the non-membership part ν –

is plotted along the ordinate. Thus, the maximal

value for each of these variables is 1, with the

classical ‘Truth’ being plotted into the (1, 0) point,

and the classical ‘Falsity’ being plotted into the (0,

1) point, while the (0, 0) point stands for the

complete Uncertainty.

Figure 1: Graphics of the points, staying for the

intuitionistic fuzzy pairs of InterCriteria consonances.

Fifth International Symposium on Business Modeling and Software Design

280

The triangle (see Figure 1) is being rendered

using the embedded class QGraphicsPolygonItem,

which is intended for plotting polygons. There are

also classes for visualization of points, but in

expected cases of multiple points (which will

significantly load the memory), the points are

directly drawn onto the background of the graphic

window. The duplicating points are removed in

advance, for the aim of improving the performance.

The drawing itself is controlled by the class of the

central window, since there are the input and output

data stored.

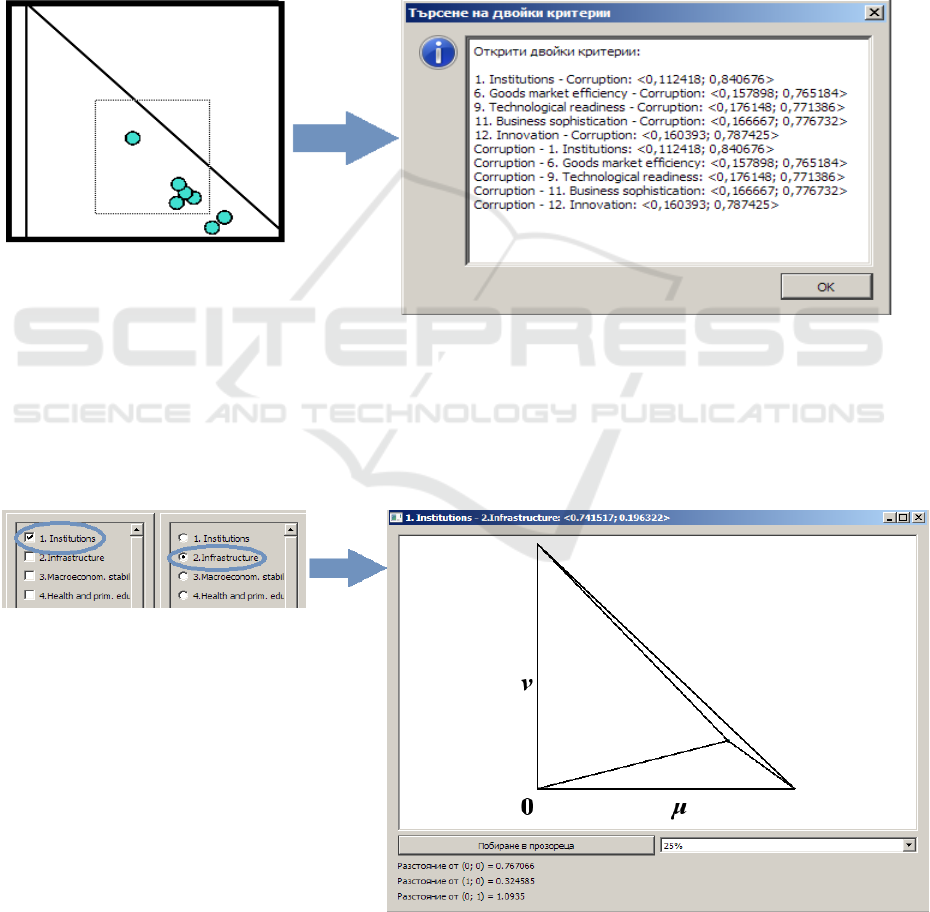
The graphic window permits scaling. Moreover,

if we want to check which pairs of criteria form a

given point, or a given area of points from the IF

triangle, we can drag with the mouse a rectangular

area around the desired points, as shown in Figure 2.

After this selection has been made, a pop-up

window appears with the names of the detected

points, i.e. pairs of criteria, as well as the values of

their coordinates, the IF membership and non-

membership factors.

Figure 2: Search for pairs of criteria, using the graphic visualization of the ICA results.

On the other hand, it can be sometimes useful to

draw the lines that connect a point in the IF triangle,

with the triangle’s vertices, together with calculation

the distances of that point from the three vertices.

This option is activated with the button ‘Distance

from vertices’, as presented in Figure 3.

Figure 3: Rendering a point and its distances from the three vertices of the IF triangle.

InterCriteria Software Design: Graphic Interpretation within the Intuitionistic Fuzzy Triangle

281

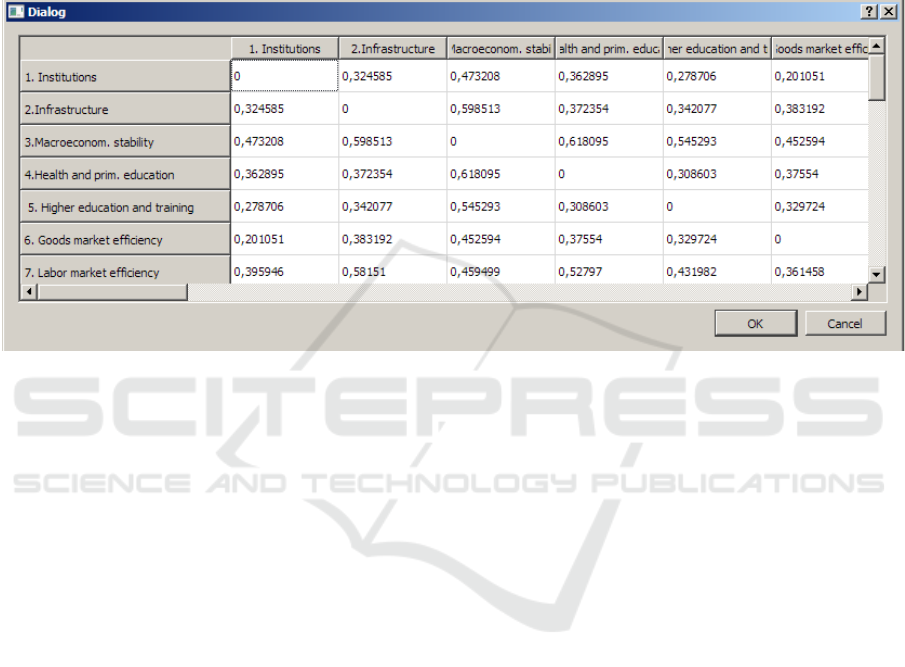
For this aim, it is necessary to pre-select two

criteria, whose InterCriteria consonance, in the form

of an IF pair, will determine the coordinates of the

point. The utilized graphic window here is the same,

with additional lines connecting the point with the

vertices, and the calculated distances. If this view

does not give enough information, the program

includes options that provide an overview of all

distances from all InterCriteria points to the

triangle’s vertices, as presented in tables related to

each vertex. These tables are opened via a separate

window using the buttons ‘Distance from [vertex

coordinates]’ in the main window. To save time, the

values here are calculated in real time only for the

visible cells from the table. The table of distances

from (1, 0) is illustrated in Figure 4.

Figure 4: Distances of all points from the vertex (1, 0) of the triangle.

4 CONCLUSION

The aim of this paper is to describe the software

design and implementation of one important aspect

of the theory of ICA which has been recently

developed theoretically (Atanassova, 2015), and was

shown to provide an alternative, and in some

situations better analysis of the results of the ICA.

Discussing the software implementation of the

ICA approach is considered by our team important,

because this allows reproducibility of the results,

obtained with the ICA method.

If necessary, other functionalities are also

possible, among which selection of consonance

thresholds, in order to sieve the criteria that are in

highest positive consonance with each other. In the

present form, the application can be successfully

used for analysis of new data, for detecting known

correlations, and discovery of new, previously

unknown correlations and knowledge.

ACKNOWLEDGEMENTS

The research work reported in the paper is partly

supported by the project AComIn “Advanced

Computing for Innovation”, Grant № 316087,

funded by the FP7 Capacity Programme (Research

Potential of Convergence Regions) and partly

supported under the Project № DFNI-I-02-5/2014.

REFERENCES

Atanassov, K. (1989). Geometrical interpretations of the

elements of the intuitionistic fuzzy objects. Pre-print

IM-MFAIS-1-89, Sofia.

Atanassov, K. (1999). Intuitionistic Fuzzy Sets: Theory

and Applications. Physica-Verlag, Heidelberg.

Atanassov, K. (2012). On Intuitionistic Fuzzy Sets

Theory. Springer, Berlin.

Atanassov K, D. Mavrov, V. Atanassova (2014).

InterCriteria decision making. A new approach for

multicriteria decision making, based on index matrices

and intuitionistic fuzzy sets. In: Issues in Intuitionistic

Fuzzy Sets and Generalized Nets, vol. 11, pp. 1–8.

Fifth International Symposium on Business Modeling and Software Design

282

Atanassova V., L. Doukovska, K. Atanassov and D.

Mavrov (2014a). InterCriteria Decision Making

Approach to EU Member States Competitiveness

Analysis. Proc. of 4th International Symposium on

Business Modeling and Software Design, 24–26 June,

Luxembourg, pp. 289–294.

Atanassova, V., L. Doukovska, D. Mavrov, K. Atanassov

(2014b). InterCriteria Decision Making Approach to

EU Member States Competitiveness Analysis:

Temporal and Threshold Analysis. P. Angelov et al.

(eds.), Intelligent Systems’2014, Advances in

Intelligent Systems and Computing, vol. 322, pp. 95–

106.

Atanassova, V., L. Doukovska, D. Karastoyanov, F.

Capkovic (2014c). InterCriteria Decision Making

Approach to EU Member States Competitiveness

Analysis: Trend Analysis. P. Angelov et al. (eds.),

Intelligent Systems’2014, In: Advances in Intelligent

Systems and Computing, vol. 322, pp. 107–115.

Atanassova V., D. Mavrov, L. Doukovska and K.

Atanassov (2014). Discussion on the threshold values

in the InterCriteria Decision Making approach. Notes

on Intuitionistic Fuzzy Sets, vol. 20, №2, pp. 94–99.

Atanassova, V., I. Vardeva (2014). Sum- and average-

based approach to criteria shortlisting in the

InterCriteria Analysis. Notes on Intuitionistic Fuzzy

Sets, vol. 20, 2014, № 4, pp. 41–46.

Atanassova V. (2015). Interpretation in the Intuitionistic

Fuzzy Triangle of the Results, Obtained by the

InterCriteria Analysis, IFSA-EUSFLAT 2015, Gijon,

Spain. (submitted).

InterCriteria Research Portal (2015). http://www.

intercriteria.net/publications.

Mavrov, D. (2015). Software for InterCriteria Analysis:

Implementation of the Main Algorithm. Proc. of 19

International Conference on Intuitionistic Fuzzy Sets.

Notes on Intuitionistic Fuzzy Sets, vol. 21 (accepted).

InterCriteria Software Design: Graphic Interpretation within the Intuitionistic Fuzzy Triangle

283