InterCriteria Decision Making Approach for Metal Chips
Briquetting
Dimitar Karastoyanov
1
, Lyubka Doukovska
1
, Stanislav Gyoshev
1
and Ivan Kalaykov
2
1
Institute of Information and Communication Technologies, Bulgarian Academy of Sciences
Acad. G. Bonchev str., bl. 2, 1113 Sofia, Bulgaria
2
Örebro University, School of Science and Technology
SE-701 82 Örebro, Sweden
Keywords: InterCriteria decision making, Index matrix, Impact briquetting.
Abstract: In the presented paper for the analysis purposes we have used experimental results of impact briquetting of
grey cast iron chips. The presented multicriteria decision making method is based on two fundamental
concepts: intuitionistic fuzzy sets and index matrices. We have named it ‘InterCriteria’ decision making
approach, which utilizes the apparatus of index matrices and intuitionistic fuzzy sets - takes an existing
multiobject multicriteria evaluation table and generates a new table that contains estimations of the pairwise
relations among the set of evaluating criteria. Our goal is to increase the efficiency of the process of
briquetting metal chips with good density and quality.
1 INTRODUCTION
Producing briquettes using metal chips and powder
is an actual scientific problem which is reflected in a
lot off publications. In paper (Bodurov et al., 2005)
is proposed an original construction of die forging
hammer propelled by industrial rocket engine. With
this machine it is possible to work with controlled
impact and with impact velocities from 4.5 [m/s] up
to 20 [m/s]. Laboratory set-up for controlled impact,
and the results of experimental study of metal chips
briquetting by controlled impact with impact speed
of 7 [m/s] are presented in paper (Gustavson et al,
2014). The potentiality to produce parts using such
briquettes is also illustrated.
The technological effects of a controlled impact
application in plastic deformation and briquetting of
metal chips processes are discussed in (Penchev et
al., 2013; Penchev et al., 2014; Penchev et al., 2014;
Radeva et al., 2014). It was found that using a
controlled impact increases the deformation up to
27% and the density of the briquettes up to 20%
when compared to the ordinary impact. In (Penchev
et al., 2014) is investigated the possibility of
processing briquettes via plastic deformation of
aluminum alloy chips (the density of the briquettes
in this case is 93% of the density of the solid alloy).
It was found that this is possible if stresses in the
deformed body are compressive. In the presented
paper for the analysis purposes we have used
experimental results of impact briquetting of grey
cast iron chips. In this study the parameters distance,
speed
, acceleration of the impacting bodies are
analysed by means of high speed camera and the
applicable software. They are part of the equipment
of the Smart Lab at IICT.
The impact energy (Е
у
) and power (F
у
) are
calculated. To get more experimental data an Xray
tomograph Nikon XTH 225 Compact Industrial CT
Scаnner has been used. This way the horizontal and
vertical briquette sections have been investigated.
The resolution of the obtained images is 5 [μm].
Based on these, we automatically determine the
briquette diameter (D [mm]) and its height (Н
[mm]), with 4
th
decimal symbol accuracy.
In process of the metal chips briquetting,
mechanical and hydraulic presses with nominal
force of several hundred to several thousand kN are
used. The goal is to obtain briquettes with good
297
Karastoyanov D., Doukovska L., Gyoshev S. and Kalaykov I.
InterCriteria Decision Making Approach for Metal Chips Briquetting.
DOI: 10.5220/0005888502970301
In Proceedings of the Fifth International Symposium on Business Modeling and Software Design (BMSD 2015), pages 297-301
ISBN: 978-989-758-111-3
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

density - the ratio H/D for different materials vary
within wide limits (H/D = 0.8 – 0.25), where H is
the height, and D is the diameter of the briquette.
The greater is the density of the briquettes, the
smaller are the losses in the transport and melting.
Basic data used to evaluate the effect of briquetting
operation is the specific density of the briquette (ρ,
[g/cm
3
]), and specific contact pressure for
briquetting (P, [MPa]).
Figure 1 shows the laboratory stand with a high
speed camera and special lighting, for taking high-
speed video recordings. Using the camera and
software makes possible to determine the speed V
y
and acceleration A
y
and then to calculate the impact
energy E
y
and the power of impact F
y
.
Figure 1: Laboratory stend for a complicated impact with
high speed camera.
2 INTERCRITERIA DECISION
MAKING APPROACH
The presented multicriteria decision making method
is based on two fundamental concepts: intuitionistic
fuzzy sets and index matrices. It is called
‘InterCriteria decision making’.
Intuitionistic fuzzy sets defined by Atanassov
(Atanassov, 1983; Atanassov, 1986; Atanassov,
1999; Atanassov, 2012) represent an extension of
the concept of fuzzy sets, as defined by Zadeh
(Zadeh, 1965), exhibiting function µ
A
(x) defining the
membership of an element x to the set A, evaluated
in the [0; 1] - interval. The difference between fuzzy
sets and intuitionistic fuzzy sets (IFSs) is in the
presence of a second function ν
A
(x) defining the non-
membership of the element x to the set A, where:
0 ≤ µ
A
(x) ≤ 1,
0 ≤ ν
A
(x) ≤ 1,
0 ≤ µ
A
(x) + ν
A
(x) ≤ 1.
The IFS itself is formally denoted by:
A = {〈x, µ
A
(x), ν
A
(x)〉 | x ∈ E}.
Comparison between elements of any two IFSs,
say A and B, involves pairwise comparisons between
their respective elements’ degrees of membership
and non-membership to both sets.
The second concept on which the proposed
method relies is the concept of index matrix, a mat-
rix which features two index sets. The theory behind
the index matrices is described in (Atanassov, 1991).
Here we will start with the index matrix M with
index sets with m rows {C
1
,…,C
m
} and n columns
{O
1
,…,O
n
}:
11 1 1 1
1
1
1
1
1, , , ,
,, ,,
,, ,,
,, ,,
,
kln
iikilin
jjkjljn
m mjmlmn
kln
CO CO CO CO
iCO CO CO CO
jCO CO CO CO
mCO CO CO CO
OOOO
M
Ca a a a
Ca a a a
Ca a a a
Ca a a a
=
KKK
KKK
MMOMOMOM
KKK
MMOMOMOM
KKK
MMOMOMOM
KKK
where for every p, q (1 ≤ p ≤ m, 1 ≤ q ≤ n), C
p
is a
criterion (in our case, one of the twelve pillars), O
q
in an evaluated object, a
C
p
O
q
is the evaluation of the
q-th object against the p-th criterion, and it is
defined as a real number or another object that is
comparable according to relation R with all the rest
elements of the index matrix M, so that for each i, j,
k it holds the relation R(a
C
k
O
i
, a
C
k
O
j
). The relation R
has dual relation
R
, which is true in the cases when
relation R is false, and vice versa.
For the needs of our decision making method,
pairwise comparisons between every two different
criteria are made along all evaluated objects. During
the comparison, it is maintained one counter of the
number of times when the relation R holds, and
another counter for the dual relation.
Let
,kl
S
μ
be the number of cases in which the rel-
ations R(a
C
k
O
i
, a
C
k
O
j
) and R(a
C
l
O
i
, a
C
l
O
j
) are simul-
taneously satisfied. Let also
,kl
S
ν
be the number of
cases in which the relations R(a
C
k
O
i
, a
C
k
O
j
) and its
dual
R
(a
C
l
O
i
, a
C
l
O
j
) are simultaneously satisfied. As
the total number of pairwise comparisons between
the object is n(n – 1)/2, it is seen that there hold the
inequalities:
,,
(1)
0
2
kl kl
nn
SS
μν
−
≤+≤
.
Fifth International Symposium on Business Modeling and Software Design
298

For every k, l, such that 1 ≤ k ≤ l ≤ m, and for
n ≥ 2 two numbers are defined:
,,
,,
2, 2
(1) (1)
kl kl
kl kl
CC CC
SS
nn nn
μν
μν ==
−−
.
The pair constructed from these two numbers
plays the role of the intuitionistic fuzzy evaluation of
the relations that can be established between any two
criteria C
k
and C
l
. In this way the index matrix M
that relates evaluated objects with evaluating criteria
can be transformed to another index matrix M* that
gives the relations among the criteria:
11 11 1 1
11
1
1,C,C ,C,C
,C ,C ,C ,C
*
.
,,
,,
mm
m m mm mm
m
CC C C
mCC C C
CC
M
C
C
μν μ ν
μν μ ν
=
K
K
MMOM
K
The final step of the algorithm is to determine
the degrees of correlation between the criteria,
depending on the user’s choice of µ and ν. We call
these correlations between the criteria: ‘positive
consonance’, ‘negative consonance’ or ‘dissonance’.
Let α, β ∈[0; 1] be given, so that α + β ≤ 1. We
call that criteria C
k
and C
l
are in:
• (α, β) - positive consonance, if µ
C
k
,C
l
> α
and ν
C
k
,C
l
< β
;
• (α, β) - negative consonance, if µ
C
k
,C
l
< β
and ν
C
k
,C
l
> α
;
• (α, β) - dissonance, otherwise.
Obviously, the larger α and/or the smaller β, the
less number of criteria may be simultaneously
connected with the relation of (α, β) - positive con-
sonance. For practical purposes, it carries the most
information when either the positive or the negative
consonance is as large as possible, while the cases of
dissonance are less informative and can be skipped.
3 EXPERIMENTAL RESULTS
The metal chips briquettes preparation with good
density and quality is of great importance for the
efficiency of this industrial process. In the presented
paper for the analysis purposes we have used
experimental results of impact briquetting of grey
cast iron chips.
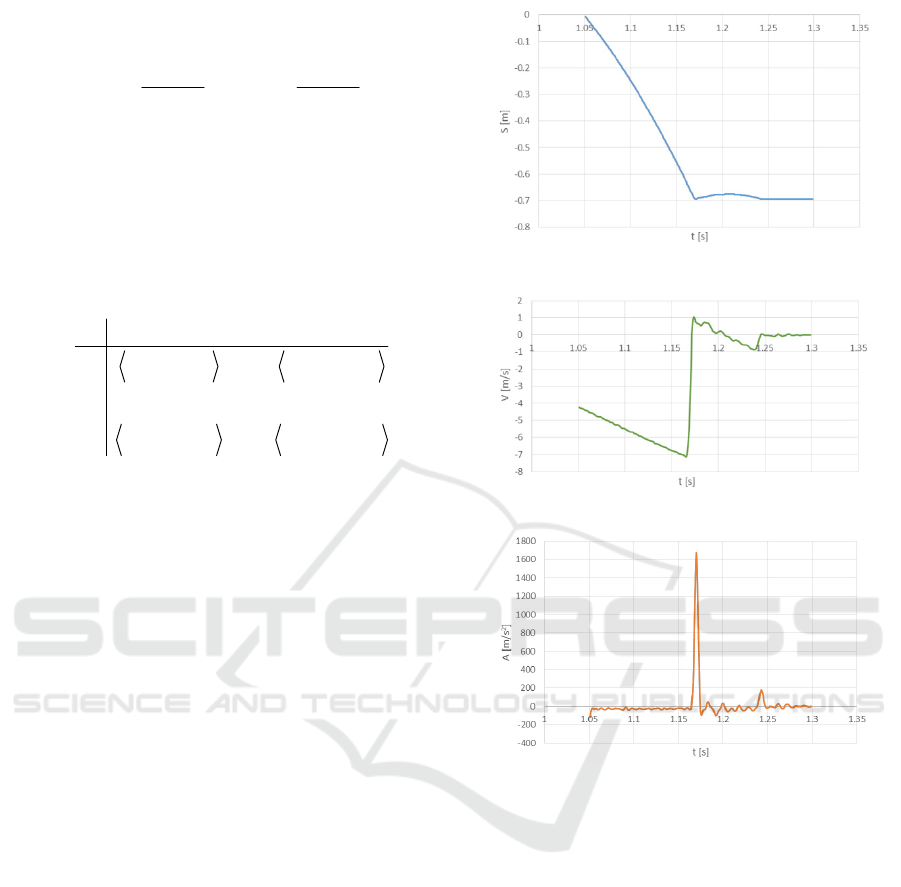
Figure 2 shows obtained experimental results for
the distance, the speed and the acceleration.
a)
b)
c)
Figure 2: Distance (a), speed (b) and acceleration (c)
diagrams in briquetting of grey cast iron chips.
In this paper are presented the results of impact
briquetting of grey cast iron chips with rectangular
shape. The average sizes are: length 25 [mm], width
15 [mm], thickness 1 [mm]. Diameter of the
produced briquettes is 20 [mm], as it is the opening
of the die for briquetting. Diameter of the punch is
19.6 [mm]. Density and quality of briquettes of these
chips are compared with those obtained in another
work of the authors using cast iron chips with
smaller sizes. It has been found that if using a
rectangular shape chips with a large size generates
briquettes with a very low density and poor quality.
From the photographs taken by X-ray tomography, it
makes clear that the reason for this is the orientation
of the chip in the peripheral wall of the briquettes,
which does not allow of the air to escape from it. It
InterCriteria Decision Making Approach for Metal Chips Briquetting
299

was concluded that in order to obtain briquettes of
cast iron chips with a large size, these chips must
first be crushed, for example in a small ball mill.
Preparation of metal chips briquettes with good
density and quality is important for the efficiency of
this process. The research conducted shows there is
no difference in the density of the briquettes made
from cleaned and not cleaned chips.
Based on the experimental research the values of
eleven parameters of grey cast iron chips briquetting
process have been obtained:
1 - V
y
– Impact speed, [m/s];
2 - A
у
– Impact acceleration, [m/s
2
];
3 - H
Δ
– Trimming height, [mm];
4 - Н – Briquette height, [cm];
5 - D – Briquette diameter, [cm];
6 - V – Briquette volume, [cm
3
];
7 - G – Briquette weight, [gr];
8 - ρ – Briquette density, [gr/cm
3
];
9 - E
у
– Impact energy, [J];
10 - E
c
– Impact specific energy, [J/cm
3
];
11 - F
y
– Power of impact, [N].
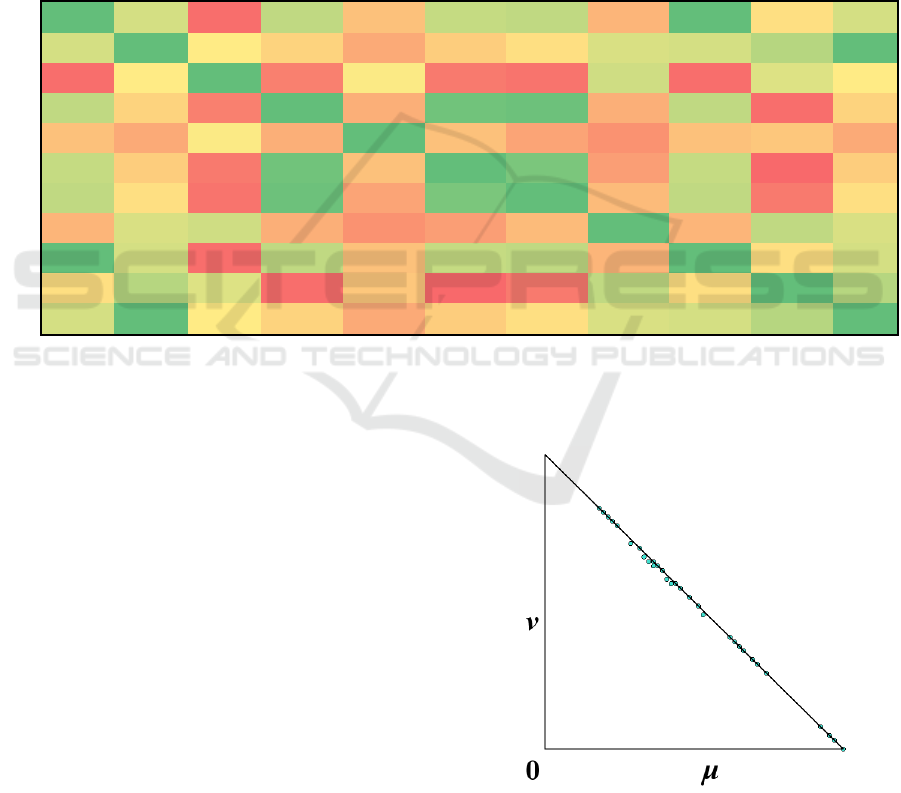
Table 1: Membership pairs of the intuitionistic fuzzy InterCriteria correlations for the grey cast iron chips.
μ 1 2 3 4 5 6 7 8 9 10 11
1
1 0.6515 0.1969 0.7121 0.4090 0.6969 0.7121 0.3787 1 0.4848 0.6515
2
0.6515 1 0.51515 0.45454 0.34848 0.43939 0.48484 0.63636 0.65151 0.74242 1
3
0.1969 0.51515 1 0.24242 0.53030 0.22727 0.21212 0.66666 0.19697 0.62121 0.5151
4
0.71212 0.45454 0.24242 1 0.36363 0.95454 0.96969 0.36363 0.71212 0.19697 0.4545
5
0.40909 0.34848 0.53030 0.36363 1 0.40909 0.33333 0.28787 0.40909 0.42424 0.3484
6
0.69697 0.43939 0.22727 0.95454 0.40909 1 0.92424 0.31818 0.69697 0.18181 0.4393
7
0.71212 0.48484 0.21212 0.96969 0.33333 0.92424 1 0.39393 0.71212 0.22727 0.4848
8
0.37878 0.63636 0.66666 0.36363 0.28787 0.31818 0.39393 1 0.37878 0.71212 0.6363
9
1 0.65151 0.19697 0.71212 0.40909 0.69697 0.71212 0.37878 1 0.48484 0.6515
10
0.4848 0.7424 0.62121 0.19697 0.42424 0.181818 0.227273 0.712121 0.484848 1 0.7424
11 0.6515 1 0.51515 0.454545 0.348485 0.439394 0.484848 0.636364 0.651515 0.742424 1
These have been analysed applying InterCriteria
decision making approach. The results are presented
in Тable 1.
The results show a strong relation between the
parameter pairs: 1 (‘Impact speed‘) – 4 (‘Briquette
height‘); 1 (‘Impact speed‘) – 7 (‘Briquette weight‘);
2 (‘Impact acceleration‘) – 10 (‘Impact specific
energy‘); 4 (‘Briquette height‘) – 6 (‘Briquette
volume‘); 4 (‘Briquette height‘) – 7 (‘Briquette
weight‘); 4 (‘Briquette height‘) – 9 (‘Impact
energy‘); 6 (‘Briquette volume‘) – 7 (‘Briquette
weight‘); 7 (‘Briquette weight‘) – 9 (‘Impact
energy‘); 8 (‘Briquette density‘) – 10 (‘Impact
specific energy‘).
Part of these relations is due to the specific
physical properties of the briquettes, which confirms
the reliability of the proposed InterCriteria decision
making approach. The benefit here is that this allows
for finding strong dependencies as well as such
where the relations are not so visible.
The geometrical visualisation of the InterCriteria
correlations for the case of iron powder briquette
onto the intuitionistic fuzzy interpretational triangle
is shown on Figure 3.
Figure 3: Geometrical visualisation of the InterCriteria
correlations for the case of iron powder briquette onto
the intuitionistic fuzzy interpretational triangle.
Fifth International Symposium on Business Modeling and Software Design
300

4 CONCLUSION
During the experiments it was seen that when
briquetting grey cast iron chips increasing the impact
specific energy to some point this increases the
density, but further increase leads to a decrease in
briquettes density. The conclusion that can be made
is that this is being influenced by the content of
carbon in the iron-carbon alloys.
The present paper proves the application of this
original InterCriteria decision making approach,
which eases the analysis if the relations between the
criteria, giving better production quality.
ACKNOWLEDGEMENTS
The research work reported in the paper is partly
supported by the project AComIn “Advanced
Computing for Innovation”, Grant №316087, funded
by the FP7 Capacity Programme (Research Potential
of Convergence Regions) and partly supported under
the Project № DFNI-I-02-5/2014.
REFERENCES
Atanassov K. (1983). Intuitionistic fuzzy sets, VII ITKR's
Session, Sofia, June 1983 (in Bulgarian).
Atanassov K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets
and Systems. vol. 20, № 1, pp. 87–96.
Atanassov K. (1991). Generalized Nets. World Scientific,
Singapore.
Atanassov K. (1999). Intuitionistic Fuzzy Sets: Theory
and Applications. Physica-Verlag, Heidelberg.
Atanassov K. (2012). On Intuitionistic Fuzzy Sets Theory.
Springer, Berlin.
Atanassov K., D. Mavrov, V. Atanassova (2013). Inter-
Criteria decision making. A new approach for multi-
criteria decision making, based on index matrices and
intuitionistic fuzzy sets. Proc. of the 12
th
International
Workshop on Intuitionistic Fuzzy Sets and General-
ized Nets, Warsaw, Poland.
Zadeh L. A. (1965). Fuzzy Sets. Information and Control
vol. 8, pp. 333-353.
Bodurov P., T. Penchev (2005). Industrial Rocket Engine
and its Application for Propelling of Forging
Hammers, Journal of Material Processing Technology,
vol. 161, pp. 504-508.
Penchev T., I. Altaparmakov (2013). Experimental
Investigations on Controlled Impact Effect,
International Conference METAL 2013, Brno.
Penchev T., S. Gyoshev, D. Karastojanov (2014). Study of
parameters of controlled impact by impact
deformation of elastic and elastic-plastic materials,
Proceedings of Recent Advances in Mechanical
Engineering Conference, 21-23.11.2014, Florence,
Italy, pp. 113-118.
Penchev T., D. Karastoyanov (2014). Experimental Study
of Upsetting and Die Forging with Controlled Impact,
International Conference on Manufacturing Science
and Engineering (ICMSE 2014), 17-18 April 2014,
Lisbon, Portugal, published in: International Science
Index, vol. 8, № 4, Part IV, e-ISSN 1307-6892, pp.
529-533.
Radeva T., I. Yatchev, D. Karastoyanov, N. Stoimenov, S.
Gyoshev (2014). Coupled Electromagnetic and
Thermal Field Modeling of a Laboratory Busbar
System, International Conference on Electrical
Engineering and Technology, ICEET 2014, 8-9
September 2014, Geneva, Switzerland, published in:
International Science Index, vol. 8, № 9, Part I, e-
ISSN 1307-6892, pp. 172-176.
Gustavson G. at al. (2014). Experimental studies and
modelling of high – velocity loaded iron-powder
compacts, Powder Technology, vol. 268, pp. 293-305.
http://www.iict.bas.bg/acomin/
InterCriteria Decision Making Approach for Metal Chips Briquetting
301