Improving Signal of Opportunity Localisation Estimates in

Multipath Environments

Thomas O. Mansfield, Bogdan V. Ghita and Adrian Ambroze

School of Computing and Mathematics, Plymouth University, Plymouth, UK

{thomas.mansfield, bogdan.ghita, m.ambroze}@plymouth.ac.uk

Keywords: Leading Edge Detection, Time of Arrival Localisation, Indoor Navigation, Signals of Opportunity.

Abstract: Network based geographic localisation has been widely researched in recent years due to the need to locate

mobile data communication nodes to a level of accuracy equivalent to that provided by global navigation

satellite systems (GNSS) in multipath urban and indoor environments. This paper investigates whether direct

sequence spread spectrum (DSSS) signal processing can be applied to narrow-band radio channels to improve

the ranging estimates. The DSSS signal processing application is then developed further to provide a method

of deriving a measurement confidence indicator, allowing the optimisation of time separated measurements

in a dynamic signals of opportunity radio environment. A set of validation tests demonstrates that the proposed

method provides a significant improvement in the accuracy and robustness of the ranging estimate compared

to simple threshold analysis in multipath environments.

1 INTRODUCTION

Radio positioning systems have achieved common

use in a diverse range of systems. The most

commonly used radio positioning systems are global

navigation satellite systems (GNSS). These systems

use signals received from satellite to calculate the

position of the user to within 4m during 95% of the

time (Norman Bonnor, 2012). GNSS systems rely on

a line of sight (LoS) view of at least 4 satellites. This

requirement cannot however, be guaranteed in urban

or indoor environments where ‘urban canyons’ and

roof cover, block sight to much of the surrounding

sky. Research has been carried out into using signals

of opportunity for localisation in such environments,

particular success has been achieved by using time of

arrival (ToA) systems to derive a user’s location

(Norman Bonnor, 2012), even in urban or indoor

environments where multipath propagation is one of

the main sources of system error 0. Constructive and

deconstructive interference between the non-line of

sight (NLoS) propagating signals can destroy or

obscure the LoS signal that is required to derive an

accurate ToA estimate.

Ultra wide band (UWB) signal analysis

techniques, originally developed for low emission

radar 0, have achieved promising results when

applied to localisation in wide bandwidth direct

sequence spread spectrum (DSSS) networks (00).

These techniques rely on the differing multipath

properties of the wide spread of frequencies to

provide an improved leading edge time of arrival

(ToA) estimate and to achieve GNSS levels of

accuracy in wide bandwidth multipath environments.

This paper builds on the use of prior art wide

bandwidth signal processing techniques and

investigates their use in signals of opportunity

networks that commonly collect time separated

narrow bandwidth measurements such as frequency

hopping spread spectrum (FHSS) networks. FHSS

networks are typical to military 0 and civilian (IEEE,

2014. IEEE 802.22) systems and challenges remain to

use them to achieve GNSS levels of location accuracy

in multipath environments 0 due to the time separated

nature of the received signals.

This paper proposes a method that allows the

system to use time separated ToA estimates and,

without prior training or additional data collection,

generate a low latency and high bandwidth filtered

ranging estimate. The benefits of the proposed

method are verified through simulation. The accuracy

and responsiveness of the ranging estimate shall be

analysed in both static and mobile receiver

environments.

This paper is organised as follows; Section 2

discusses the prior art. Section 3 proposes a method

to use the leading edge detection algorithm to extract

O. Mansﬁeld T., Ghita B. and Ambroze A.

Improving Signal of Opportunity Localisation Estimates in Multipath Environments.

DOI: 10.5220/0005889200430048

In Proceedings of the Fourth International Conference on Telecommunications and Remote Sensing (ICTRS 2015), pages 43-48

ISBN: 978-989-758-152-6

the data required to weight the values in a recursive

filter. Section 4 provides details of the simulation

environment and evaluates the ranging estimate

performance. Section 5 concludes and discusses

further work.

2 PRIOR ART

2.1 Leading Edge Detection

Basic ToA detection systems commonly use simple

threshold based leading edge detection 0), which

relies on the assumption that the LoS message will

arrive first via the shortest direct path. In many

situations however, the LoS component may be

heavily attenuated by deconstructive multipath

interference providing a leading error driver for

indoor or urban ranging system accuracy.

Search-back algorithms improve on the ToA

accuracy by analysing the received packet and

performing a search-back to determine physical layer

properties of the message to determine the time of

arrival more robustly (Haneda K., 2009). These

algorithms require prior knowledge of the multipath

environment which cannot be provided in many

applications.

The Multiple Signal Classification (MUSIC)

algorithm (Schmidt R. O. 1986) extends the analysis

to allow multipath signals to be used as a further

information source and has become widely used in

research. This algorithm requires a substantial

training period to determine the number of multipath

signals present to achieve better performance than

relying on leading edge detection alone. Again, a

training period is not practical in many applications

where the device is to be used to navigate around an

unknown area.

UWB signal processing techniques utilise the

wide frequency range of the received signals to

provide an improved ToA estimate. The analysis of

the full frequency range available allows the user to

determine frequency specific multipath variations

and make an improved estimation of the true ToA

reading. A widely implemented example of an

existing UWB signal processing technique, described

in 0, has been selected for further development in this

paper. This technique was developed to detect the

leading edge of a signal obtained from a wide

bandwidth transmission. It has been selected for

further development due to the fact that the running

filters applied to the raw data may provide additional

data to the user following further analysis.

The UWB signal processing technique is applied

to any wide band received data as follows: if h(t)

represents the received signal in the time domain, it is

first passed through a rectified moving average filter

as shown in (1).







nti

thabs

]))([(

)(

(1)

The averaged signal y[t] is then passed through two

filters of sizes n

and n

which return the maximum

value from a sliding window, as shown in (2) and (3).

max_n

[t]= max(y

t -n

...y

)

(2)

)...max(][max_

2 tnt

yytn





(3)

A binary indicator of whether a leading edge has been

detected can be obtained from (4).

)][(max_&

])[max_2*][(max_][

threshtn

tntntr





(4)

The threshold detection level, thresh, is typically set

to 3σ of inter message in-channel received signal

noise.

2.2 Application Considerations for

Navigation Filters

Recursive averages are commonly used in navigation

systems to produce a low noise and low latency

location estimate from a noisy measurement input. In

order to provide an efficiently filtered output, the

measurement system that populated the recursive

filter must provide not only a measurement value, but

also a dynamic confidence indicator.

When using a simple threshold detection

algorithm to detect the leading edge of a received

signal, the only information that can be provided to

the navigation filter is the time when a received value

is greater than the selected threshold. If this

information is available for each FHSS channel, a

simple un-weighted recursive filter shown in (5) can

be constructed to update the users filtered location

based on the its previous position and the latest sensor

data where, as commonly used in filter notation,

represents the filter output,

represents the previous

state and

represents the latest sensor value. The

measurement confidence is represented by α.

Fourth International Conference on Telecommunications and Remote Sensing

xxx

)1(





(5)

The filter represented in (5) may be tuned by

adjusting the value of α by a predetermined value.

A value of α < 0.5 reduces the noise of the filter

output at the expense of a higher latency if the

receivers true location changes. A value of α > 0.5

generates a more responsive, lower latency filter

output but the filter output noise will be adversely

affected. Both of these options are unsuitable for

many system applications.

3 PROPOSED METHOD

The leading edge detection algorithm described in

section 2.1 has been developed for wide band signal

processing and analyses all of the data from the wide

frequency range with each measurement.

The receiver system to be developed by this paper

makes a ranging estimate upon detection of the

leading edge of a received signal using the signal

processing technique described in section 2.1. The

process of running the n

filter (3) to return the

maximum value in the longer sliding window

continues for the duration of the first message in the

current FHSS channel. The data obtained from the

maximum value sliding windows is placed into a

column vector and a standard deviation taken to

determine the presence and magnitude of multipath

present throughout the message. This is then

correlated to provide a numerical confidence value.

The process is represented in equations (6) and

(7). The standard deviation, σ, is first calculated in (6)

with n

as the filter length, x

is each iterative filter

value and x

is the current filter average. This

standard deviation is then normalised in (7) to

produce a dynamic measurement confidence, α.







)(

ain



(6)

)1(









(7)

α represents a confidence factor with a weighted

value between 0 and 1 for low to high confidence

measurements respectively. This confidence measure

can then be used to dynamically tune the filter shown

in (5) to generate a recursive filter input that benefits

from both low noise and low latency. This has been

achieved by providing a high weighting value to

ranging estimates received with good confidence and

a low weighting to estimates with a low confidence,

even if there has been true movement by either the

transmitter or receiver.

The ability to achieve this from a multipath data

source dynamically and without prior knowledge is of

a key benefit in higher level navigation systems, as

discussed in section 2.2. This confidence weighting

has been achieved without the use of any additional

information or averages over the ones implemented to

allow the improved leading edge detection.

4 SYSTEM VALIDATION

4.1 Simulator Validation

A simulated radio frequency (RF) environment was

modelled in Matlab® and Simulink® to evaluate the

effectiveness and performance of the techniques

discussed in section 3. The simulation uses the

standard multipath simulation model (Alsindi N.A,

2004) shown in (8) where L

is the number of

multipath components, α is the complex attenuation

and τ is the propagation delay.









)()(

tth



(8)

The simulation assumes that an idealised

transmitter generates a single frequency modulated

pulse; for validation, the FHSS network parameters

included 100 20 kHz channels evenly spaced from 3

to 5 GHz. The transmitted pulse is then subjected to

empirically derived propagation and receiver

distortions to produce a received signal for analysis.

The resulting signal includes simulated effects of

multipath with the use of separate propagation

channels, the number of which can be set by the user.

The simulations evaluated throughout this paper will

consider a LoS propagation path of 10 m with several

multipath reflection paths with an apparent time path

from the transmitter to the receiver consistent with

10.1 m to 11.2 m propagation distances.

This simulated environment has been used to

ascertain the performance of a simple threshold

detection algorithm in a Monte Carlo based

simulation of a wide range of FHSS channels in a

fixed geometry. A typical single transmitted message

and the received signal patterns in a high multipath

environment can be seen in Fig 1.

Improving Signal of Oppourtunity Localisation Estimates in Multipath Environments

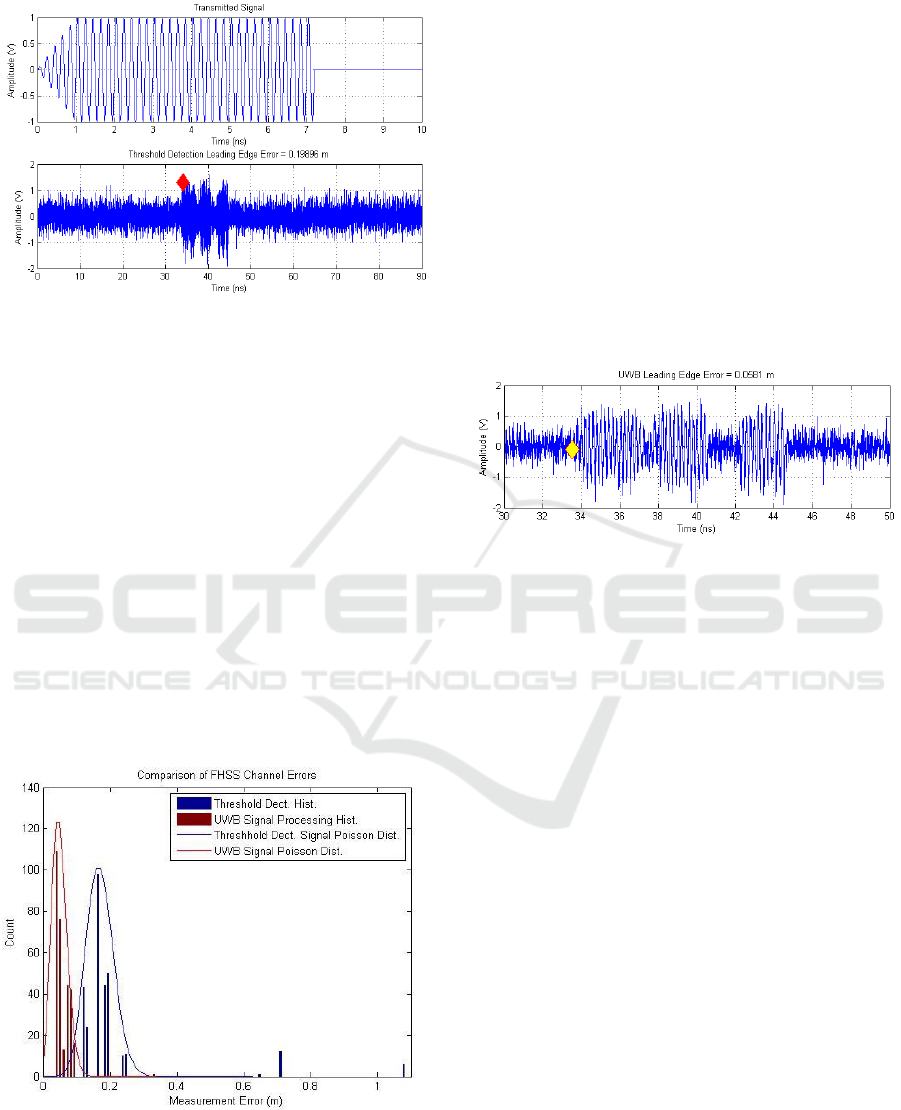
Figure 1: Transmitted (top) and received (bottom) pulse

with the location of the detected leading edge of the pulse

marked by the red symbol.

The threshold detection algorithm has been

simulated assuming a static receiver and transmitter

across a range of FHSS channels to benchmark the

simulation. The results can be seen in Fig. 2 and

shows properties that are expected in multipath

environments, as seen in (Norman Bonnor, 2012)]

and 0). The similarity to data collected by practical

test in previous research provides confidence that the

simulation is representative.

4.2 Technique Validation

A comparison of edge detection seen by employing

UWB signal processing techniques to each narrow

bandwidth channel as opposed to simple threshold

detection can be seen in Fig. 2.

Figure 2: Comparison of threshold based and UWB signal

processing leading edge detection methods.

Analysis shows that the Poisson distribution

variance has a λ value of 17 for the threshold

detection algorithm and an improved λ value of 5 for

the UWB threshold detection. The received estimates

across the range of networks not only have less

average error but also a greater distribution density

than can be obtained from simple threshold detection

alone. As well as a significant improvement in the

Poisson distribution, the UWB based edge detection

algorithm removes the erroneous outliers seen at ≈ 0.7

m and ≈ 1.1 m error in the threshold detection

algorithm. This behaviour may account for the high

multipath uncertainty seen in (Faragher R. M., 2007)

where a simple threshold detection algorithm was

used to detect the ToA to estimate range.

Detail of the detected trigger timing at the leading

edge of a signal with light multipath is shown in Fig.

Figure 3: UWB leading edge detection of pulse in a noisy

multipath environment.

Figure 3 is a magnification of the area of interest,

related to the transmission pulse as shown in Fig. 2.

Areas of constructive and deconstructive multipath

effects can be seen throughout the 34 ns to 42 ns

region where a non-multipath signal would be

expected to produce a stable series of 1 V peaks.

The simulation has shown that the evaluation tests

for the UWB algorithms discussed in section 2.1

produce a significant improvement over threshold

detection when providing ToA estimation in high

multipath FHSS networks when only a single narrow

bandwidth channel can analysed at a time.

Further to the improvement shown in ToA

estimates in a high multipath environment, the

application of the additional data available, described

in section 3, to a recursive navigation filter is

analysed in the remainder of this section.

The application of threshold analysis data, where

no weighting data is available for the new samples,

into the simplified recursive filter leads to a noisy and

poorly filtered position estimate. Fig 4. compares a

plot of the raw measured and filtered ranging estimate

obtained from a simulation of a static system that

sweeps through 100 FHSS channels over a 5 second

period.

Fourth International Conference on Telecommunications and Remote Sensing

Figure 4: The raw and filtered output from the threshold detection

algorithm with a pre-selected static confidence interval.

The results displayed in Figure 4 verify that the

filtered position estimate from an un-weighted

recursive filter is comparatively noisy and produces a

large filtered error in the event of a multipath

leading edge detection received from the sensor, as

seen approximately 0.2 seconds into the simulation.

The application of the position estimates and the

relative variance derived using the method described

in section 3 has been applied to a weighted navigation

filter. The application of this navigation filter in the

simulation leads to improved stability to the position

estimate which, combined with the improvement in

leading edge detection reliability and the absence of

outliers, leads to a greatly improved position estimate

over the threshold detection algorithm, as shown in

Fig. 5.

Figure 5: The raw and filtered output from the navigation filter

with UWB leading edge detection and dynamically obtained

confidence interval. This should be compared with Fig 6 to see the

improvement achieved.

In a physically static system, as simulated in Fig 4

and Fig. 5, where the relative position of the

transmitter and receiver does not change, the

sensitivity to erroneous data could be mitigated by

weighting the raw sensor data by a pre-determined

factor of < 1 depending on sensor noise. While this

will limit the filter error in the event of erroneous

multipath readings and produce a more accurate

location estimate, it also introduces high latency if the

receiver or transmitter truly moves location. The

application of a dynamically weighted recursive filter

prevents an erroneous multipath ToA reading from

causing filter noise. If however, the system truly

moves, a new filter input with a new position estimate

with a high weighting will be received and the filter

output will respond with little latency.

A further simulation was run to evaluate the effect

of a true receiver motion on the filter output. To

simplify the simulation, a single narrow bandwidth

channel with no frequency hopping was used

throughout the experiment. After approximately 1.2s

into the simulation, the receiver node instantaneously

moves 1m within a multipath environment and

remains static for the remainder of the simulation.

Fig. 6 shows a comparison of the filter response

to the applied motion with both threshold detection

and UWB detection inputs.

Figure 6: The response of the filters to an instantaneous 1 m

movement of the receiving node.

The threshold detection filter still has a greater

error before and after the 1 m move of the receiver

node than the UWB filter, as expected. The area of

interest highlighted by this simulation is the

difference in time taken for the filter output to identify

the change in location. The dynamic weighting to

allows the UWB filter to respond with minimal

latency in the event of true receiver or transmitter

movement. The improvement seen in Fig 6 is due to

both the improved UWB ranging estimate, shown in

Fig 2 and the ability to weight the measurements.

These contributing factors have not been analysed

separately due to the fact that the weighted recursive

Improving Signal of Oppourtunity Localisation Estimates in Multipath Environments

filter may be implemented without any additional

data collection and should always be used to provide

an optimised solution.

5 CONCLUSIONS AND FURTHER

WORK

This paper proposed a set of algorithms and

application techniques that improve narrow

bandwidth channel ranging estimates in signals of

opportunity environments. The novel application and

further development of DSSS signal processing

techniques to provide not just an improved ranging

estimate but, by re-analysing existing data, an

additional confidence weighting.

By re-analysing the available data, a filter

confidence factor can be obtained that can be

calculated dynamically without the need for a training

period and without any prior knowledge of the radio

system and environment. More specifically, the use

of UWB signal processing techniques provided an

approximately 4 times improvement in ranging

estimation over simple threshold detection even in

narrow bandwidth channels, including a better

Poisson distribution and higher resilience to false

detections.

The main benefit of applying this technique is that

a filtered ranging estimate can be obtained that is

more accurate, lower noise and lower latency than can

be obtained by using simple threshold detection

techniques to detect the leading edge of a message.

The analysis of the proposed technique

performance throughout this paper has been carried

out only in multipath environments. It is anticipated

that the benefits of the technique will be significantly

less apparent in less hostile environments.

Future work should include the physical test of

this system to verify the model. The integration of the

algorithm into higher level systems is also required to

verify the higher level benefits shown during

simulation. The close coupling of this system with

higher level navigation systems, in particular Kalman

filtering schemes may also allow the development of

a significantly improved signal of opportunity based

localisation system.

REFERENCES

Air Commodore Norman Bonnor, 2012. A Brief History of

Global Navigation Satellite Systems, Royal Institute of

Navigation Journal of Navigation vol. 65.

Faragher R. M, Duffett-Smith P.J, 2010. Measurements of

the effects of multipath interference on timing accuracy

in a radio positioning system, IET Radar, Sonar and

Navigation, vol. 4, iss. 6, pp. 818-824.

Fontana R. J., 2004. Recent System Applications of Short-

Pulse Ultra-Wideband (UWB) Technology. Published in

IEEE Microwave Theory and Techniques, Vol. 52, Issue

Mahfouz M. R., et. al, 2008. Investigation of high accuracy

indoor 3-D positioning using UWB technology, IEEE

Trans. Microwave Theory and Technology, pp. 1316-

1330.

Merkl B., 2008. The future of the operating room: surgical

preplanning and navigation using high accuracy ultra

wide-band positioning and advanced bone

measurement, Ph.D Dissertation, The University of

Tenessee, USA.

Grumman Northrop, 2013. Understanding Voice and Data

Link Networking, Guidebook, Northrop Grumman, San

Diego, USA.

IEEE, 2014. IEEE 802.22 Working Group – Enabling

Broadband Wireless Access Using Cognitive Radio

Technology http://www.ieee802.org/22/ Accessed 14

November 2014.

Xu P., Palmer R.J and Jiang Y, 2005. An Analysis of

Multipath for Frequency Hopping Spread Spectrum

Ranging. IEEE Conference on Electrical and Computer

Engineering.

Haneda K., 2009. Performance Evaluation of Theshold

Based UWB Ranging Methods – Leading Edge vs,

Search Back, 2rd European Conference on Antennas

and Propagation.

Schmidt R. O. 1986, Multiple Emitter Location and Signal

Parameter Estimation, IEEE Trans. Antennas

Propagation, Vol. AP-34 (March 1986), pp.276-280

Alsindi N.A, 2004. Performance of TOA Estimation

Algorithms in Different Indoor Multipath Conditions.

PhD Thesis, Worcester Polytechnic Institute.

Faragher R. M., 2007. Effects of Multipath Interference on

Radio Positioning Systems, Ph.D. dissertation, Dept.

Physics., University of Cambridge, Cambridge

Fourth International Conference on Telecommunications and Remote Sensing