
Big data in Neurosurgery: Intelligent Support
for Brain Tumor Consilium
Karol Kozak
1,2
1
Medical Faculty, Dresden University of Technical, Fetscherstraße 74, D-01307 Dresden, Germany
2
Wrocław University of Economics, Komandorska 118/120, Wrocław, Poland
karol.kozak@uniklinikum-dresden.de
Keywords: Big data in medicine, Machine learning, Neurosurgery, Consilium, Radiology
Abstract: A brain tumor occurs when abnormal cells form within the brain. Medical imaging plays a central role in the
diagnosis of brain tumors. When a brain tumor is diagnosed, a medical team will be formed (consilium) to
assess the treatment options presented by the leading surgeon to the patient and his/her family. Using historical
evidence-based healthcare data and information directly extracted from images to categorize them may
support to increase decision for treatment of patient with brain tumor. Due to its complexity, cancer care is
increasingly being dependent on multidisciplinary tumor consilium. That is why it is very important to avoid
emotional and quick decisions done by members of consilium. Few studies have investigated how best to
organize and run consilium in order to facilitates important decision about patient therapy. We developed and
evaluated a multiparametric approach designed to improve the consilium ability to reach treatment decisions.
In particular the use of discriminative classification methods such as support vector machines and the use of
local brain image meta-data were empirically shown to be important building blocks as support for therapy
assign. For efficient classification we used fast SVM classifier with new kernel method.
1 INTRODUCTION
Brain tumors have mainly two types. First is benign
tumors are unable of spreading beyond the brain
itself. Benign tumors in the brain generally do not
essential to be treated and their progress is self-
limited. Sometimes they can cause complications
because of their position and surgery or radiation can
be helpful. And second is malignant tumors are
typically called brain cancer. These tumors can extent
outside of the brain. Malignant tumors of the brain
will always change into a problem if left untreated
and a violent approach is almost always warranted.
Brain malignancies can be divided into two
categories. Primary brain cancer originates in the
brain. Secondary or metastatic brain cancer extents to
the brain from another site in the body. Cancer arises
when cells in the body (in this case brain cells) divide
without control. Generally, cells divide in a
structured manner. If cells keep separating
uncontrollably when new cells are not needed, a mass
of tissue forms, called a progress or tumor. The term
cancer generally refers to malignant tumors, which
can attack nearby tissues and can extent to other parts
of the body. A benign tumor does not extent. Last
year, an estimated 22,850 adults (12,900 men and
9,950 women) in the United States will be diagnosed
with primary cancerous tumors of the brain and spinal
cord. It is estimated that 15,320 adults (8,940 men and
6,380 women) will die from this disease this year.
About 4,300 children and teens has been diagnosed
with a brain or central nervous system in last year.
More than half of these are in children younger than
15 (Cancer.net, 2015).
Thanks to the rapid development of modern
medical devices and the use of digital systems, more
and more medical images are being generated. This
has lead to an increase in the demand for automatic
methods to index, compare, analyse and annotate
them. Care for brain tumors is increasingly complex
and often requires specialized expertise from multiple
disciplines. Brain tumor consilium reviews provide a
multidisciplinary approach to treatment planning that
involves doctors from different specialties reviewing
69
Kozak K.
Big data in Neurosurgery - Intelligent Support for Brain Tumor Consilium.
DOI: 10.5220/0005889600690075
In Proceedings of the Fourth International Conference on Telecommunications and Remote Sensing (ICTRS 2015), pages 69-75
ISBN: 978-989-758-152-6
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and discussing the medical condition and treatment of
patients (National Cancer Institute, 2012).
In large university hospitals, several terabytes of
new data need to be managed every year. Typically,
the databases are accessible only by alphanumeric
description and textual meta information through the
standard Picture Archiving and Communication
System (PACS). Data mining can be defined as the
process of finding previously unknown patterns and
trends in existing tumor images and using that
information to build predictive models for consilium
decision support (Kincade, 1998).
Alternatively, it can be defined as the process of
data selection and exploration and building models
using vast data stores to uncover previously unknown
patterns (Milley, 2000).
The underlying Digital Imaging and
Communication in Medicine (DICOM) protocol
supports only queries based on textual content and
limited number of parameters present on the DICOM
file and defined by the modality (DICOM, 2011).
DICOM files contain their modality as part of the
meta-data. We suggest to use that information, feature
extraction mechanism can take context into account
into the feature extraction and decision support
process.
The purpose of our study is to automate extraction
of DICOM Metadata from the PACS over patients
population for specific brain tumor and support brain
tumor consilium in making decision for applied
therapy. An Support Vector Machine (SVM)
classification technique is proposed to recognize in
reasonable malignant and benign MRI brain image
from historical database in PACS.
2 METHOD
The first step is to automatically extract dicom images
semantic and similarity information and expose that
information to a classifier in a very efficient way.
Figure 1. Decision support system for brain tumor consilium. Metadata information from large population of dicom images
is analysed by SVM.
Fourth International Conference on Telecommunications and Remote Sensing
70
The most direct approach to get decision based on
images is to match image volume features directly. In
this context, content means some property extracted
from the image such as color and intensity
distribution, texture, shape, or high level features
such as the presence of nodes or objects of interest.
This approach however is generally not feasible as it
may not be clear which volume from one dicom
image correspond to which volume in the other
image. DICOM objects consist of sets of attribute-
value pairs that allow nesting (the values can be other
DICOM objects). There are several thousand
official attributes, an extension mechanism for
private attributes and 27 data types called value
representations (VR) for the values (DICOM Part 5,
2011). The data type for each official at tribute is
fixed.
Official attributes are identified by a group and
element number (16bit unsigned integers usually in
hexadecimal notation). Attributes can also represent
some kind of real world entity that is only implicitly
defined by DICOM or some kind of abstract
entity created by the particular hospital. There are
important metadata such as pixel parameters,
acquisition index, patient dose and geometric
information that are generated by the modality and
transferred to the PACS database as DICOM
metadata.
We have divided metadata into feature sets.
General dicom image features, which can be
extracted from PACS and can therefore be applied to
queries over brain tumor category, and modality
specific features. Our concept relies on the automatic
extraction of attributes from a dicom image to provide
the multiparameters for classifier (Fig. 1).
2.1 Classification
An Support Vector Machine classification technique
is proposed to recognize malignant and benign tumors
from MRI brain images (meta-data).
a) b)
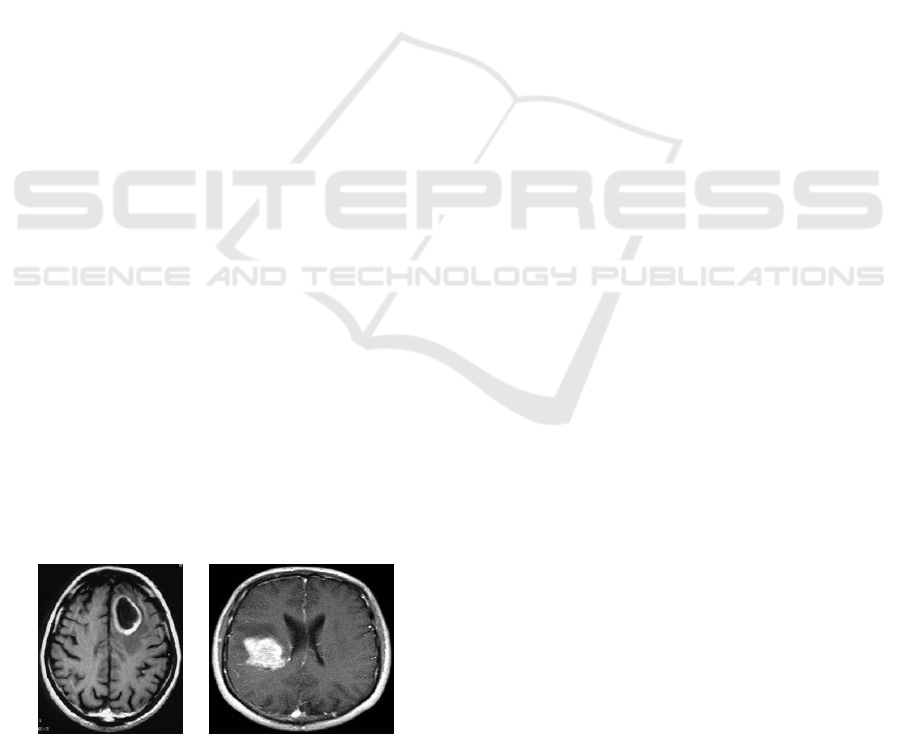
Figure 2: DICOM images of a a) benign and b) malignant
brain tumor.
Benign tumors have well defined edges and are
more easily removed surgically. Malignant tumors
have an irregular border that invades normal tissue
with finger-like projections making surgical removal
more difficult. Image source: a) http://neurosurgery.
ufl.edu and b) http://cdn.phys.org
2.2 Fast SVM
SVM is one of the successful approaches to
multiparametric data analysis. In supervised
classification we have a set of data samples (each
consisting of measurements on a set of variables) with
associated labels, the class types (malignant, benign).
These are used as exemplars in the classifier design.
The classification experiments in dicom analysis
were carried out with a support vector machine
(SVM) (Vapnik, 1995).
Discriminative approaches to recognition
problems often depend on comparing distributions of
features, e.g. a kernelized SVM, where the kernel
measures the similarity between histograms
describing the features. In many practical cases where
performance of classification is significant SVM with
standard kernel function like Gaussian Kernel (GK)
or Radial Basis Function (RBF) are not suitable.
Recently, the use of kernels in learning systems
has received considerable attention. The main reason
is that kernels allow mapping the data into a high
dimensional feature space in order to increase the
computational power of linear machines (see for
example Vapnik, 1995, 1998, Cristianini and Shawe-
Taylor, 2000).
SVM can be optimized for performance via the
kernel methods adapted for dicom image datasets. In
Kernel methods, the original observations are
effectively mapped into a higher dimensional non-
linear space. For a given nonlinear mapping, the
input data space X can be mapped into the feature
space H:
).(:: xxxwhereHX
(1)
Linear classification in this non-linear space is
then equivalent to non-linear classification in the
original space. Require Fisher LDA can be rewritten
in terms of dot product.
)()(),(
jiji
xxxxK
(2)
Unlike Support Vector Machine (SVM) it doesn’t
seem the dual problem reveal the kernelized problem
Bigdata in Neurosurgery: Intelligent Support for Brain Tumor Consilium
71

naturally. But inspired by the SVM case we make the
following key assumption,
i
ii
xw )(
(3)
In terms of new vektor the objective J (
)
becomes,
W
T
B
T
R
S
S
J
n
)(maxarg
(4)
Table 1: Most popular kernels used for SVM classification.
Kernels
Formula
Linear
K(x, x’)= x. x’
Sigmoid
K(x, x’) = tanh(a x. x’+b)
Polynomial
K(x, x’) = (1+ x. x’)
d
RBF
K(x, x’) = exp(-
|| x - x’||
2
)
Gaussian
K(x, x’) = exp(-
|| x - x’||)
Table 1 present most popular kernel methods.
Correspondingly, a pattern in the original input space
R
n
is mapped into a potentially much higher
dimensional feature vector in the feature space H.
The scatter matrices in kernel space can expressed
in terms of the kernel only as follows:
][][
2211
TTTT
KKKKKKKK
S
B
(5)
)(
222111
2 TT
W
KKNKKNKS
(6)
psoitiveim
im
K
N
K
1
1
1
negativemi
im
K
N
K
,
2
2
1
(7)
Nji
ij
K
N
K
,
1
(8)
Popular choice is the Gaussian kernel
)
2
||||
exp(),(
2
2
ji
jiK
(9)
with a suitable width of kernel and must σ > 0.
So, we have managed to express the problem in
terms of kernels only which is what we were after.
Note that since the objective in terms of has exactly
the same form as that in terms of w.
In this project the input dicom image is not
directly fed into SVM as inputs. Instead, a set of
simple features is first extracted from meta-data, and
then the features are used as inputs. It will be assumed
that each dicom image meta-data set z = {b
1
, . . . , b
M
}
is composed of a set of range-bearing measures b
i
=
(αi, di) where αi and di are the bearing and range
measures, respectively
Each training example for the SVM algorithm is
composed by one observation z
i
and its classification
υ
i
. The set of training examples is then given by
E =
{(z
i
, υ
i
) : υ
i
Υ = {benign, malignant}}
(10)
where Υ is the set of classes. In this paper it is
assumed that the classes of the training examples are
given in advance (benign, malignant). The objective
is to learn a classification system that is able to
generalize from these training examples and that can
later classify day/night in laboratory environment.
Kernel SVMs have become popular for real-time
applications as they enjoy both faster training and
classification speeds, with significantly less memory
requirements than non-linear kernels due to the
compact representation of the decision function
(Subhransu et. al, 2008 ). The crossplane kernel, KH
I
(t
a
, t
b
) = n
i
=1 min (t
a
(i), t
b
(i)) is often used as a
measurement of similarity between histograms ta and
t
b
, and because it is positive definite (Odone et.al,
2005) it can be used as a kernel for discriminative
classification using SVMs. Recently, crossplane
kernel SVMs (call CPSVMs), have been shown to be
successful for detection and recognition (Grauman
and Darrell, 2005 and 18. Lazebnik et.al, 2006).
We based on kernel Intersection Kernel (Subhransu
et. al, 2008). Given feature vectors (parameters from
DICOM meta-data) of dimension n and learned
support vector classifier consisting of m support
vectors, the time complexity for classification and
space complexity for storing the support vectors of a
standard CPSVM classifier is T (p u).
.
Fourth International Conference on Telecommunications and Remote Sensing
72

Figure 3: Classification model.
We apply an algorithm for CPSVM classification
with time complexity T (u log p) and space
complexity T(pu). We then use an approximation
scheme whose time and space complexity is T (u),
independent of the number of support vectors. The
key idea is that for a class of kernels including the
crossplane kernel, the classifier can be decomposed
as a sum of functions, one for each histogram bin,
each of which can be efficiently computed. In dicom
anaylsus with thousands of support vectors we also
observe speedups up to 2000× and 200× respectively,
compared to a standard implementation.
Now we show that it is possible to speed up
classification for CPSVMs. For feature vectors x, z
, the crossplane kernel is:
(11)
and classification is based on evaluating:
(12)
Thus the complexity of evaluating h(x) in the
naive way is O(pu). The trick for crossplane kernels
is that we can exchange the summations in equation
12 to obtain:
(13)
Rewriting the function h(x) as the sum of the
individual functions, hi, one for each dimension,
where
(14)
So far we have gained nothing as the complexity of
computing each hi(s) is T(p) with an overall
complexity of computing h(x) still T(pu). We now
show how to compute each hi in T(logp) time.
Consider the functions hi(s) for a fixed value of i.
Let
denote the sorted values of x
l
(i) in
increasing order with corresponding
s and labels
as
and
.
If
then h
i
(s) = 0,
otherwise let r be the largest integer such that
.
Bigdata in Neurosurgery: Intelligent Support for Brain Tumor Consilium
73

Then we have,
(15)
Where we have defined,
(16)
(17)
Equation 17 shows that hi is piecewise linear.
Furthermore hi is continuous because:
=
(18)
Notice that the functions A
i
and B
i
are
independent of the input data and depend only on the
support vectors and α. Thus, if we precompute h
i
(
r
)
then h
i
(s) can be computed by first finding r, the
position of s =
l
in the sorted list (i) using binary
search and linearly interpolating between h
i
(
r
) and
h
i
(
r
+1). This requires storing the
l
as well as the
h
i
(
l
) or twice the storage of the standard
implementation. Thus the runtime complexity of
computing h(x) is T(u logp) as opposed to T(pu), a
speed up of T(u/logp). In our experiments we
typically have SVMs with a few thousand support
vectors and the resulting speedup is quite significant.
3 RESULTS
In order to show the validity and classification
accuracy of our algorithm we performed a series of
tests on few dicom benchmark data sets. Data sets are
presented in table 2. We tested a proposed extension
of Intersection Kernel in experimental datasets from
sample collection dicoms. We use the standard SVM
algorithm for binary classification described
previously. The regularization factor of SVM was
fixed to C = 10. In order to see the effect of
generalization performance on the size of training
data set and model complexity, experiments were
carried out by varying the number of training samples
(30, 60, 120, 180, 240) according to a 5-fold cross
validation evaluation of the generalization error. The
data was split into training and test sets and
normalized to minimum and maximum feature values
(Min-Max) or standard deviation (Std-Dev).
Table 2: DICOM images dataset for astrocytoma brain
tumors from demo dataset. Datasets are divided in
malignant tumors and benign tumors.
Total
Training
data
Test
data
Images
840
420
420
Malignant
tumors
260
130
130
Benign
tumors
580
290
290
Results for our classifier are presented in table 3.
Table 3. Classification results for two datasets from two patients using two kernel methods with c = 20.
Dataset 1: Malignant tumors
Training
set
Kernel
RBF
Training
Time/
Classification
Time
Classification
Accuracy
Intersection
Kernel
Training
Time/
Classification
Time
Classification
Accuracy
30
C = 20
16 s / 3s
83.6%±6.7
C = 20
11 s /3s
84.7%±1.6
60
C = 20
27 s / 6s
84.2%±2.6
C = 20
12 s / 4s
85.5%±6.7
120
C = 20
35 s / 10s
85.6%±5.5
C = 20
24 s / 10s
86.2%±1.5
180
C = 20
38 s / 18s
87.2%±1.5
C = 20
22 s / 13s
88.3%±4.3
240
C = 20
48 s / 19s
82.4%±3.9
C = 20
33 s / 17s
82.6%±2.5
Fourth International Conference on Telecommunications and Remote Sensing
74
Dataset 2: Benign tumors
Training
set
Kernel
RBF
Training Time/
Classification
Time
Classification
Accuracy
Intersection
Kernel
Training Time/
Classification
Time
Classification
Accuracy
30
C = 20
14 s / 5s
83.6%±6.7
C = 10
12 s /3s
84.4%±2.6
60
C = 20
27 s / 9s
82.3%±2.5
C = 10
16 s / 4s
82.9%±5.5
120
C = 20
32 s / 12s
85.0%±4.4
C = 10
23 s / 11s
87.1%±1.7
180
C = 20
40 s / 15s
83.1%±1.5
C = 10
27 s / 13s
85.2%±3.4
240
C = 20
45 s / 18s
85.5%±2.7
C = 10
35 s / 13s
82.8%±1.6
4 CONCLUSION
The accuracy of the SVM for classifying
malignancies was by average 85.4% (28s) and the
negative bening tumors predictive value, 83.61%
(24s). The SVM proved helpful in the decision based
on imaging diagnosis of brain tumor. The
classification ability of the SVM with fast Kernel is
nearly equal to that of the standard SVM model, but
the SVM with fast kernel has a much shorter training
and prediction time (1 vs 189 seconds). Given the
increasing size and complexity of data sets, the SVM
is therefore preferable for computer-aided decision
support. Our method has the potential to predict
therapy strategy in fast time, saving a significant
amount of time to consilium experts, giving them
suggestions, enabling them to quickly move from a
single observation object image to a set of similar
ones, potentially containing historical decisions in
therapy. These supporting decisions, when compared
to the current patient dicom image, may strengthen
the case for the diagnosis or provide the consilium
with additional insight.
REFERENCES
(2011) Digital imaging and communications in medicine
(DICOM) part 7: Message exchange. Section 9.1.2.
National Electrical Manufacturers Association.
(2011) Digital Imaging and Communications in Medicine
(DICOM), Part 5: Data Structures and Encoding,
Section 6.2 http://medical.nema.org/ Dicom/
2011/11_05pu.pdf
Cancer Center http://www.cancer.net
CDN Physics: http://cdn.phys.org
Cristianini, N. and J. Shawe-taylor, (2000). An introduction
to Support Vector Machines. 200.11/year
Cortes, C. and Vapnik, V. (1995). Support-vector
networks. Machine Learning. 213. 94
Grauman, K. and Darrell, T. (2005). The pyramid match
kernel: Discriminative classification with sets of image
features. ICCV, 2.
Kincade, K. (1998). Data mining: digging for healthcare
gold. Insurance & Technology, 23(2), IM2-IM7
Lazebnik, L., Schmid, C. and Ponce, J. (2006). Beyond
bags of features: Spatial pyramid matching for
recognizing natural scene categories. In CVPR.
Milley, A. (2000). Healthcare and data mining. Health
Management Technology, 21(8), 44-47
National Cancer Institute. Definition of Tumor Board
Review, (2012).
Cancer http://www.cancer.gov/dictionary?cdrid=322893.
Neurosurgery http://neurosurgery.ufl.edu and
Odone, A., Barla, F. , Verri, A. (2005) Building kernels
from binary strings for image matching. IEEE T. Image
Processing, 14(2):169–180.
Subhransu, Z. M., Berg, A. C. Malik, J. (2008)
Classification using Intersection Kernel Support Vector
Machines is Efficient. IEEE Computer Vision and
Pattern Recognition.
Vapnik, V.N. (1995). The Nature of Statistical Learning
theory, Springer Verlag, New York.
Bigdata in Neurosurgery: Intelligent Support for Brain Tumor Consilium
75
