Constraint Multi-objective Optimization based on Genetic Shuffled

Frog Leaping Algorithm

Sun Lu-peng and Ma Ge

College of Information Science & Technology, Zhengzhou Normal University, ZhengZhou, Henan, 450044, China

slp2060@163.com

Keywords: Shuffled Frog Leaping Algorithm, Multi-objective, Constraints.

Abstract: To solve the convergence problem of the constrained multi-objective optimization, combining the

advantages of genetic algorithm and shuffled frog leaping algorithm a method based on genetic shuffled

frog leaping algorithm. To use the genetic operators and the packet improved shuffled frog leaping

algorithm and avoid falling into local optimal, accelerating the convergence speed. Experiments show that

the improved algorithm is efficient and reasonable, can reduce the execution time of the multi-objective

optimization problem, improve the quality of optimal solution.

1 THE CONSTRAINT

MULTI-OBJECTIVE

OPTIMIZATION

In the real world, the problem of optimization with

multi-objective constraint, under certain conditions,

the optimization problems are multi-objective, in

most cases, multi-objective to be optimized

attributes with conflicting. For example, the

investment problem, we hope to use the least

investment cost and the lowest risk, to gain the

maximum benefit. If there is no priori knowledge,

this kind of problem solving is very difficult by the

single objective optimization. The multi-objective

optimization problem ( MOP)

[1]

, which is defined as

follows:

If there are n variables and k objective function

of multi-objective problem, describe its

formalization:

{

1 2

m a x { ( ) , ( ) ,.. . , ( ) }

. . ( ) { ( ) , ( ) ,. .. , ( ) ) 0

y f x f x f x

S T e x e x e x e x

= ≤

Among them, x= (x1, x2,... , xn) X, X is the

decision vector, X represent the decision space

formed by the decision vector y= (y1, y2,... , yK)

Y, y is the target vector, Y formed by the target

vector target space constraints, e (X) ≤ 0 determines

the range of x.

Constrained multi-objective optimization goal

can not find a single solution, the optimal solution is

a set, is to ensure that the set of Pareto optimal

solutions close to the true Pareto optimal solution set

and evenly distributed on the basis of satisfying the

constraints, the complexity of the greater. At present,

the traditional method of constrained multi objective

optimization are

[2]

: objective weighting method,

the multi-objective optimization problem into a

single objective optimization problem; the single

objective function as the optimization objective, the

other goal function to solve the constraints; the

goal programming method to set the objective

function for the intended target, find out the closest

or expected value solution. Traditional

multi-objective optimization methods is difficult,

mainly reflected in: one can only obtain a Pareto

optimal solution; the Pareto frontier is concave,

Lu-peng S. and Ge M.

Constraint Multi-objective Optimization based on Genetic Shufﬂed Frog Leaping Algorithm.

DOI: 10.5220/0006019700940099

In Proceedings of the Information Science and Management Engineering III (ISME 2015), pages 94-99

ISBN: 978-989-758-163-2

can not find the Pareto optimal solution; the

traditional method requires the priori knowledge.

Evolutionary algorithm is a group search

algorithm, can have multiple Pareto optimal

solutions in a single execution, and the different

problems (non continuous, non differentiable

problem solving)

[3]

. In the optimization of

constrained multi objective treatment, improves the

convergence and diversity algorithm. More and more

studies the evolutionary algorithm, and achieved

great success, but the number of multi-objective

evolutionary algorithms are generally not more than

4 , its stability is relatively poor, to find the optimal

solution efficiently and further research is needed.

2 SHUFFLED FROG LEAPING

ALGORITHM

Shuffled frog leaping algorithm is a heuristic search

algorithm.in 2003, Eusuff and Lansay formally

proposed shuffled frog leaping algorithm

[4][5]

, search

by heuristic function, and find the optimal solution.

In this algorithm, the memetic algorithm as the

foundation, combined with the optimization

algorithm and particle swarm optimization.

2.1 The Principle of the Algorithm

In 1989, Moscato proposed Memetic algorithms

(MA, meme) as chromosomes carry genetic

information, only to be transmitted or repeated when

it can be called memo, the algorithm uses the

competition and cooperation mechanism in the local

strategy, which can be used to solve large-scale

discrete optimization problem, can solve the other

algorithm cannot solve the problem.

In 1995, Eberhart and Kennedy proposed particle

swarm optimization algorithm according to the birds

of prey behavior simulation of simplified social

model

[6]

. The algorithm is composed of a plurality of

particle groups to a certain speed in D dimensional

search space flight, each particle to search other

particles within the relevant range phase of merit,

and on the basis of the position change

[7]

. The

particle velocity and position formula as follows:

1 1

1 2

( ) ( )

k k k k k k

iD iD iD iD gD gD

V V c p x c p x

ξ η

+ +

= + − + −

1 1

k k k

i D i D i D

x x V

+ +

= +

The C1, C2 as the study factor, the particles have the

ability to self summary and excellent learning within

the field of particles, the particles into the history of

the advantages of continuous approximation; ,

[0,1], is a uniform distribution random number

intervals, xi x

,…,x

) is the i particle position

, P

, p

,... P

), best historical point particles

experienced pg=(pg

,pg

,…,pg

) the best point

particle through.

In 1998, Shi and Eberhart into the inertia weight

in the algorithm, improves the convergence

performance of the algorithm, the velocity formula

(2) to:

1 2

( ) ( )

k k k k k k

i D i D i D i D g D g D

V v c p x c p x

ω ξ η

= + − + −

Among them, Omega is the inertia weight, its value

can make the particles with balancing exploration

ability and exploitation ability. When = 1, the

basic particle swarm optimization algorithm is a

standard.

A group of cooperative search algorithm shuffled

frog leaping algorithm by simulating the frog

foraging and produce

[8]

, transfer by individual and

group information, the global information exchange

and local search effectively combined. The whole

wetland frog is set to a population, the population is

divided into several sub populations in small

populations, each has its own culture, every frog also

have other effects and individual self culture, and

Constraint Multi-objective Optimization based on Genetic Shuffled Frog Leaping Algorithm

Constraint Multi-objective Optimization based on Genetic Shufﬂed Frog Leaping Algorithm

with the evolution of the population evolution, when

these sub populations evolve to a certain extent, will

these sub populations were mixed, realize

information exchange, until a termination condition

is satisfied. The global leap exchange and the local

depth search strategy so that the algorithm can jump

out of local optimum to the global optimum

direction, evolution.

2.2 The Algorithm Flow

Step 1: population initialization: within the feasible

solution space, randomly generated initial population

of F, the whole population containing k m*N frog.

Where m is the number of sub populations, namely

the number of memeplex, n is the number of each

sub population contains frog. Dimension D, each

frog position represents a candidate solution, the I

frog position F (i) adaptive value is denoted by fi.

Step 2: the entire population in the k frog

according to the fitness values in descending order,

generating a group number X {F(i),f

;i=1,2,…,k},

when i=1, said the frog's best position.

Step 3: on the whole population according to

k=m*n divided into m groups Y

,…,Y

expressed

as:

[ ( ), | ( ) ( ( 1)), ( ( 1)), 1,2,..., ]

k j j

Y F j f F j F k m j f f k m j j n

= = + − = + − =

he first frogs into Y

subgroup, second frogs into Y

so tired, the m frog into the Ym, the m+1 frog is

divided into Y

, until all the frogs distribution date.

Step 4: in each sub population memeplex, every

frog affected other frogs, keep close to the goal.

Mainly uses the memetic evolution, the process is as

follows:

(1) counting im initialization of Memeplex ,im=

0, iterations iN=0 ,each evolution, the frog

information exchange between individuals, the worst

frog position to improve position;

2 im=im+1

3 iN=iN+1

(4) for moving the position of each frog, frog

mobile distance cannot exceed the maximum

distance moved;

(5) if the frog to move to a better location,

representation yields better solutions, with the new

location of the frog instead of frog, or use the best

point in the history of frog pg replace the position of

sub populations best frog pb, repeat the above

action;

(6) if the operation does not produce new, then

randomly generated a new location instead of the sub

populations at the worst frog pw;

(7) if iN<N, then go to the (2);

(8) if im<m, then go to the (1).

Step 5: the frog after memetic evolution, the sub

populations were mixed, to adapt to the values are

sorted, and update the best position of the whole

population of frogs.

Step 6: a termination condition is satisfied, then

the end, or to jump to the Step 3.

2.3 The Algorithm Parameter Setting

The algorithm needs to set 5 parameters: the number

of initial clusters in the frog k, k value is greater,

showing the number of initial samples of the larger,

compute the optimal solution is more likely; number

of sub populations of m because k=m*n, m size of

the direct impact of the a number of frogs each

subgroup of n, if the n value is too small, the

advantages of memetic evolutionary search will not

exist; allows the frog to move the maximum distance

, the values and the ability to control algorithm for

global search, the value is too large, may skip the

optimal solution, capacity is too small will reduce

global search; maximum algebra of the entire

population, and scale proportional to the size of the

value of the maximum number of iterations; sub

populations of N, might fall into the local optimal

ISME 2015 - Information Science and Management Engineering III

ISME 2015 - International Conference on Information System and Management Engineering

value is too large, too small will weaken the

information exchange between individuals.

3 IMPROVED SHUFFLED FROG

LEAPING ALGORITHM

Shuffled frog leaping algorithm is relatively strong

ability in global search, but if the problem is more

complex, then the problems of slow convergence

speed and easily falling into local extremum

problem, genetic algorithm has the ability to jump

out of the local optimum, therefore, will be shuffled

frog leaping algorithm combined with genetic

algorithm to form the genetic shuffled frog leaping

algorithm (G-SFLA).

Differences between G-SFLA and SFLA is to

adopt the genetic algorithm crossover and mutation

operations on packet evolution, these two operations

used in the process of Step 4.

The crossover operation refers to the same position

of random performance best frog Pb and the poor

performance of frog Pw set breakpoints, the right

part of the breakpoints are exchanged, generating

two new process called cross. If the new position is

better than Pw, instead of Pw. If the solution is not

superior to Pw, the random Pw bits of mutation

operation, thus creating new solutions instead of Pw.

G-SFLA, the group also makes some

improvements, the grouping method of SFLA, the

last group of individual relative fitness of relatively

poor individuals in the whole population, even if the

group members constantly through the information

exchange and learning, it is unable to get a better

evolution results. Because of uneven packet,

limitation of the study amplification. A new way of

grouping is based on the original packets, randomly

from the other group took several individuals joined

the group, the number of the members of the group

are n+m-1, diversity is obtained with genetic

arithmetic, play the advantage of. Note that, when

the team re merged into a population, the number of

individuals in a population increase of m* (m-1),

sorted again for all individuals, remove duplicate

individual. The number of individuals removed more

than k, from the previous K individuals to iterate the

next round, if less than k individuals, randomly

generated individuals, make up the K for the next

round of iteration.

4 SIMULATION EXPERIMENTS

This experiment in order to verify the performance

of G-SFLA, comparing with the shuffled frog

leaping algorithm, the experimental results are

analyzed. The experimental function using 3

benchmark functions, as shown in table 1: The

experimental parameters are set as follows: the

population of 500 frog, is divided into 25 sub

groups, frogs have 20 each subgroup of SFLA,

G-SFLA in 25 (adding 5), in the subgroup of 20

times of iteration, the individual search range is

Xmax/5, evolutionary iteration times is 1000, the

algorithm running 25 time. In the condition of same

parameters, the experimental results on SFLA and

G-SFLA two kinds of algorithm (Table 2) were

compared, analysis of the pros and cons.

Table 1: The Test Object.

Function Function Expression

Range

Standard

Solution

Sphere

∑

[-100,100]

Schwefel

( sin | |) 418.982 9

x xi n

− +

∑

[-500,500]

Ackley

1 1

20exp[ 0.2 ] exp[ 2 ] 20

n n

i i

x x e

n n

= =

− − − + +

∑ ∑

[-32,32] 0

Constraint Multi-objective Optimization based on Genetic Shuffled Frog Leaping Algorithm

Constraint Multi-objective Optimization based on Genetic Shufﬂed Frog Leaping Algorithm

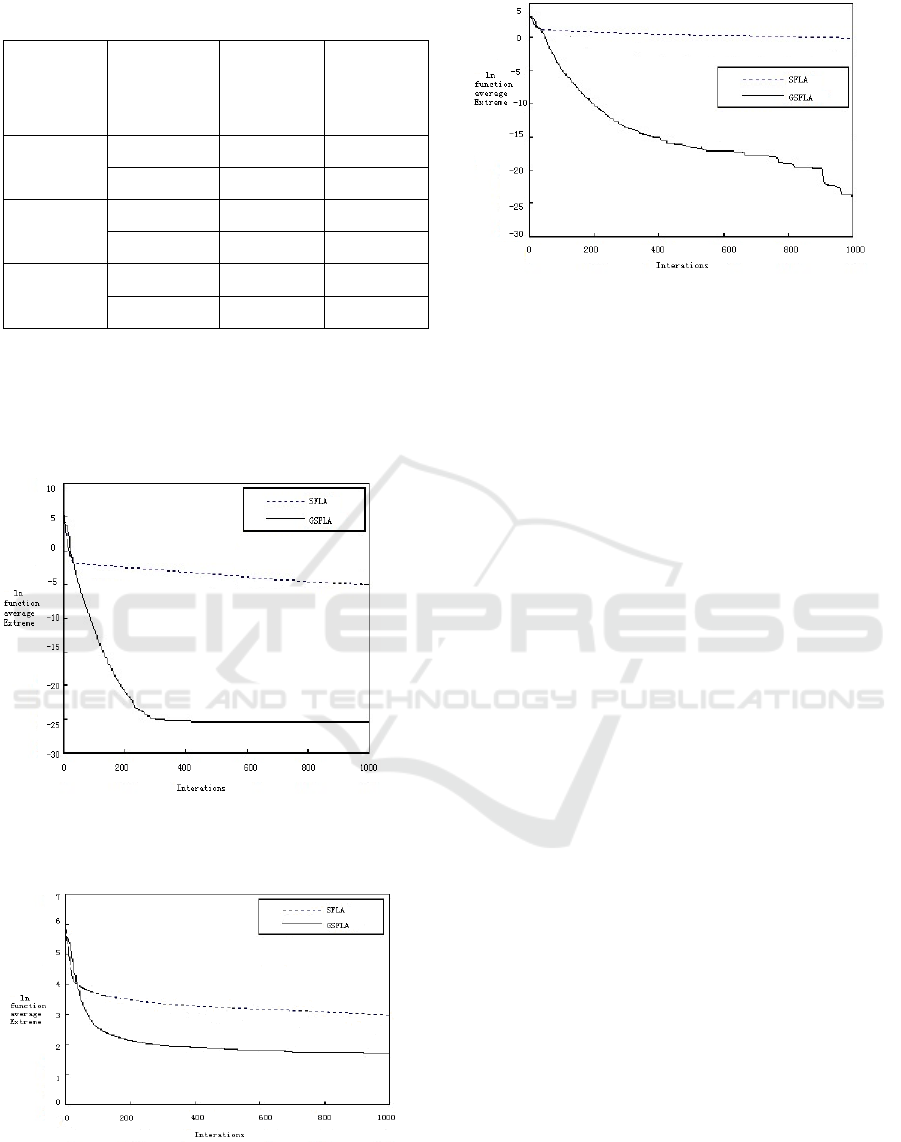
Table 2: The experimental results.

Function Algorithm

The average

optimal

value

standard

deviation

Sphere

SFLA 0.00573 0.00286

G-SFLA 2.3E-16 4.72E-16

Schwefel

SFLA 0.92186 0.18636

G-SFLA 0.00304 0.00017

Ackley

SFLA 0.79385 0.65802

G-SFLA 1.82E-13 5.42E-13

Figure 1- Figure 3 are three curves that function

respectively by SFLA and G-SFLA algorithm

independent running average value obtained after 25

times of evolution.

Figure 1: The evolutionary curve of Sphere.

Figure 2: The evolutionary curve of Schwefel.

Figure 3: The evolutionary curve of Ackley.

Through the above three in the chart, the

constrained multi objective optimization, the

performance of G-SFLA is better than SFLA, in the

target optimization accuracy under the same number

of iterations, G-SFLA is obviously lower than

SFLA. The above results show that, G-SFLA has

better stability and convergence.

5 CONCLUSION

Based on the advantages of shuffled frog leaping

algorithm and genetic algorithm, design a constraint

multi-objective genetic algorithm based on shuffled

frog leaping algorithm. Experiments show that, in

the parameter is small, the G-SFLA algorithm has

faster convergence speed, can in the iteration times

less access to better solutions.

REFERENCE

E. Zitzler, L. Thiele, ”Multiobjective Evolutionary

Algorithms: A Comparative Case Study and the

Strength Pareto Approach”, IEEE Transactions on

Evolulionary Compution , vol.3,no.4, November

1999,257-271.

H-P. Sehwefel, ”Kybernetische Evolution als Strategie der

experimentellen Forschung in derStromungstechnik,”

Diploma thesis, Technical University of Berlin,1965.

ISME 2015 - Information Science and Management Engineering III

ISME 2015 - International Conference on Information System and Management Engineering

K. Deb, Multi-Objective Optimizarion using Evolutional

Algorithms. Chicester,UK:John Wiley&Sons,2001

Eusuff M & K E Lansey. Optimization of water

distribution network design using the shuffled frog

leaping algorithm[J]. Water Resources Planning and

Management,2003,129(3):210-225.

Rahirni-Vahed, A., Mirzaei, A. H.. A hybrid

multi-objective shuffled frog- leaping algorithm for a

mixed-model assembly line sequencing Problem[J].

Computer & Industrial Engineering (2007),

doi:10.1016/j.eie.z007.06.007

Ziyang Zhen & Daobo Wang & Yuanyuan Liu. Improved

Shuffled Frog Leaping Algorithm for Continuous

optimization Problem[C].IEEE Congress on

Evolutionary ComPutation ,2009:2992-2995

Emadl Elbeltagi & Tarek Hegazy & Donald Grierson.

Comparison among five evolutionary-based

optimization algorithm[J].Advanced Engineering

Informaties,2005,19(l):43- 53

E. Zitzler, M. Laumanns, L.Thiele,”SPEA2:Improving the

strength pareto evolutionary algorithm,” in

Evolutionary Methods for Design, Optimization and

Control with Applications to Industrial Problems,

Athens, Greece, 2002,95-100.

Author Introduction:

1. Sunlupeng (1970.3-), male, Henan Zhengzhou,

Master Degree, lecturer, research direction of

computer application.Email:slp2060@163.com

2. Mage (1983.1-), male, Henan Zhengzhou, Master

Degree, lecturer, research direction of computer

application.Email:mage0608@163.com

Constraint Multi-objective Optimization based on Genetic Shuffled Frog Leaping Algorithm

Constraint Multi-objective Optimization based on Genetic Shufﬂed Frog Leaping Algorithm