Grey Prediction on Cage Dynamic Behavior of Cylindrical Roller
Bearing
L. Chen, X. T. Xia and M. Qiu
Henan University of Science & Technology, Luoyang 471003, China
Keywords: Grey Dynamic Model, Cylindrical Rolling Bearing, Cage Displacement, Grey System Theory, Prediction.
Abstract: Dynamic behaviour of a cage in cylindrical roller bearing is a nonlinear kinetic and it is a key factor which
influences applying performance of the bearing. Its displacements are forecasted by means of the grey
dynamic model GM (1, 1). Residual test and posteriori error test are conducted to verify the reliability of the
results of prediction. The experiment shows that the method proposed has the high precision and satisfy the
engineering demand.
1 INTRODUCTION
Radial cylindrical roller bearings are designed to
carry heavy radial loads and are suitable for high
speed applications (Moore, R., Lopes, J, 1999).
When cylindrical bearing operated, they generate
vibrations and noise. The principle forces, which
drive these vibrations, are time varying nonlinear
contact forces, which exist between the various
components of the bearings: raceways, rollers and
cage (Smith, J., 1998).
The importance of energy efficiency has been
increasing and has become a quality criterion for
bearing producers and users in recent years. Hence,
more and more researchers drew their attention on
dynamic behaviours on the cage. Houpert developed
simulation software to simulate cage behaviour and
relative experimental validation was carried out
(Houpert, L., 2010). Harsha analysed the nonlinear
dynamics analysis of ball bearings due to cage run-
out and number of balls (Harsha, S. P., 2006). The
conclusion of his work showed that obtained FFT
due to non-uniform spacing the ball passage
frequency was modulated with the cage frequency.
In some special applications, the data responding
cage dynamic behaviour in future can prevent the
disaster when the bearing is applied in key
equipment’s. In past years, many researchers applied
the theory in predicting future data. For rolling
bearing, the friction torque drew a lot of attentions
by researches. For example, Xia et al. researched a
dynamic prediction model for rolling bearing
friction torque using the grey bootstrap fusion
method and chaos theory. Xia et al., forecasted
rolling bearing friction torque by dynamical GM
[1,1] model (Xia, X. T., Lv, T. M, 2012). In this
paper, dynamic behavior of cage in cylindrical roller
bearing is involved in the research as another
performance parameter. The prediction values are
compared with experiment values. The small
deviations between them confirm the validity of the
calculation model.
2 GREY PREDICTION MODEL
GM (1, 1) model of Grey System Theory is widely
used in prediction realm. It is a time serious
forecasting model, encompassing a group of
differential equations adapted for parameter
variance, rather than a first order differential
equation.
The original data state sequence X (0) can be given
by
X (0) = (x (0) (1), x (0) (2),..., x(0) (i),..., x(0) (n))
(1)
Where x(0)(i) is the ith datum in X(0) and n is the
number of the data in X(0).
The AGO information of X
(0)
can be defined as
X
(1)
=(x
(1)
(1), x
(1)
(2),..., x
(1)
(k),..., x
(1)
(n))
(2)
Where
x
(1)
(k)=
(0)
1
()
k
i
x
i


,k=1,2,…,n
(3)
The GM (1, 1) model can be whiten by establishing
457
Qiu M., Chen L. and Xia X.
Grey Prediction on Cage Dynamic Behavior of Cylindrical Roller Bearing.
DOI: 10.5220/0006028504570460
In Proceedings of the Information Science and Management Engineering III (ISME 2015), pages 457-460
ISBN: 978-989-758-163-2
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
457

a first order differential equation
x
(1)
(k) as
(1)
dx
dt
+
(1)
()ax t =b
(4)
The solution to the whitening differential equation is
x

(1)
(k+1)=(x
(0)
(1)-
b
a
)e
-ak
+
b
a
, k=1,2,…,n-1
(5)
In which
(a,b)
T
= (B
T
B)
-1
B
T
Y
(6)
with
Y = (x
(0)
(2), x
(0)
(3),..., x
(0)
(n))
T
(7)
and
(1)
(1)
(1)
1
(2)
1
(3)
1
(n)
z
z
B
z












(8)
The reduction sequence can be given by
X

(0)
= (
x

(0)
(1),
x

(0)
(2),...,
x

(0)
(k),...,
x

(0)
(n))
(9)
where
x

(0)
(k+1) =
x

(1)
(k+1) -
x

(1)
(k)
(10)
3 TEST MODEL
A grey model needs to be tested to determine
whether it is reasonable. Only through the model test
it can be used to predict. Two test methods are
proposed in this work.
3.1 Residual Test
The residual sequence is defined as

=

(1),

(2),…,

(n))=(x
(0)
(1)-
x

(0)
(1), x
(0)
(2)-
x

(0)
(2),…, x
(0)
(n)-
x

(0)
(n))
(11)
The relative error sequence is defined as

=(

(1),

(2),…,

(n))=(
(0)
(1)
(1)
x

,
(0)
(2)
(2)
x

,…,
(0)
()
()
n
x
n

)
(12)
For k≤n, the average relative error is given by

=
1
1
()
n
k
k
n



(13)
with
()k

=
(0)
()
(k)
k
x

(14)
The average precision is defined as
p
0
= (1-

)✕100%
(15)
3.2 Posteriori Error Test
Posteriori error test is a statistical concept, which is
in accordance with the probability distribution of the
residuals, to evaluate the accuracy of a model.
Posteriori error test can be divided in 4 steps as
following.
The 1
st
step is calculating the mean
x
and the
variance
2
1
s of X
(0)
x
=
(0)
1
1
()
n
k
x
k
n


(16)
2
1
s =
(0) 2
1
1
(())
n
k
x
kx
n



(17)
The 2
nd
step is calculating the mean

and the
variance
2
2
s of

:

=
1
1
()
n
k
k
n



(18)
2
2
s =
(0) 2
1
1
(())
n
k
k
n





(19)
The 3
rd
step is calculating the posterior error ratio C
and the small error probability P:
C=
2
1
S
S
(20)
P=


1
( ) 0.674kS  
(21)
The 4
th
step is determining the precision of the
model according to the precision grade shown in
Table 1.
ISME 2015 - Information Science and Management Engineering III
458
ISME 2015 - International Conference on Information System and Management Engineering
458

Table 1: Precision scale.
Precision grade P C
Good >0.95 <0.35
Qualified >0.80 <0.5
Barely qualified >0.70 <0.65
Unqualified ≤0.70 ≥0.65
4 CASE STUDY
A cylindrical roller bearing typed as NU2310G1 is
chosen as an example for case study. All the
coordinates are expressed in the right-handed
Cartesian coordinate system. While the outer ring is
fixed in space, the inner ring rotates clockwise about
the -X axis and the radial load is in the +Z direction.
Gravity is in the -Z direction. Tab.2 shows the
specifications of the test bearing and running
conditions.
Measurement of cage behavior is carried out
using two eddy-current displacement gauges for
both Y and Z directions. The reason for using two
gauges for the X direction is to check the cage for
absence of conical oscillation.
Fig.1 to Fig.4 are the comparison of experiment
data and simulation results. Fig.1 and Fig.2 are the
comparison of data at +X and –X sides from Y
direction, respectively. Similarly, Fig.3 and Fig.4 are
the comparison of data at +X and –X sides from Z
direction, respectively.
0.2
0.25
0.3
0.35
0.4
0 200 400 600 800 100 0
mm
ms
exper imentaldata
predictedda ta
Figure 1: Comparison of experimental data and predicted
data from Y direction at +X side.
0
0.05
0.1
0.15
0.2
0.25
0 200 400 600 800 100 0
mm
ms
exper imentaldata
predicteddata
Figure 2: Comparison of experimental data and predicted
data from Y direction at -X side.
0.2
0.25
0.3
0.35
0 200 4 00 600 8 00 100 0
mm
ms
experimentaldata
predicteddata
Figure 3: Comparison of experimental data and predicted
data from Z direction at +X side.
0
0.05
0.1
0.15
0.2
0 200 400 6 00 8 00 1 00 0
mm
ms
experimentaldata
predicteddata
Figure 4: Comparison of experimental data and predicted
data from Z direction at -X side.
The simulation results begin at the 6th datum,
and the 6th datum is predicted by the 1st to the 5th
datum of original data sequence. Similarly, the 7th
datum is predicted by the 2nd to 6th datum of
original data sequence, so on and so forth. As can be
seen in the four figures, the variation tendency of the
two curves is parallel, and the difference between
data is relatively small.
Table 2: Test bearing and operating conditions.
Parameter /Unit Value
Bearing Size /mm
Ø50✕Ø 100✕40
Number of rollers 12
Basic static load rating /N 131000
Cage type
Machined, Outer ring land
riding
Radial internal clearance/ µm 40
Cage guide clearance, mm 0.445
Lubricant VG56, Air-oil lubrication
Rotational speed/ RPM 3000
Radial load /N 4900
Temperature of outer ring at
O.D. /°C
35
 3
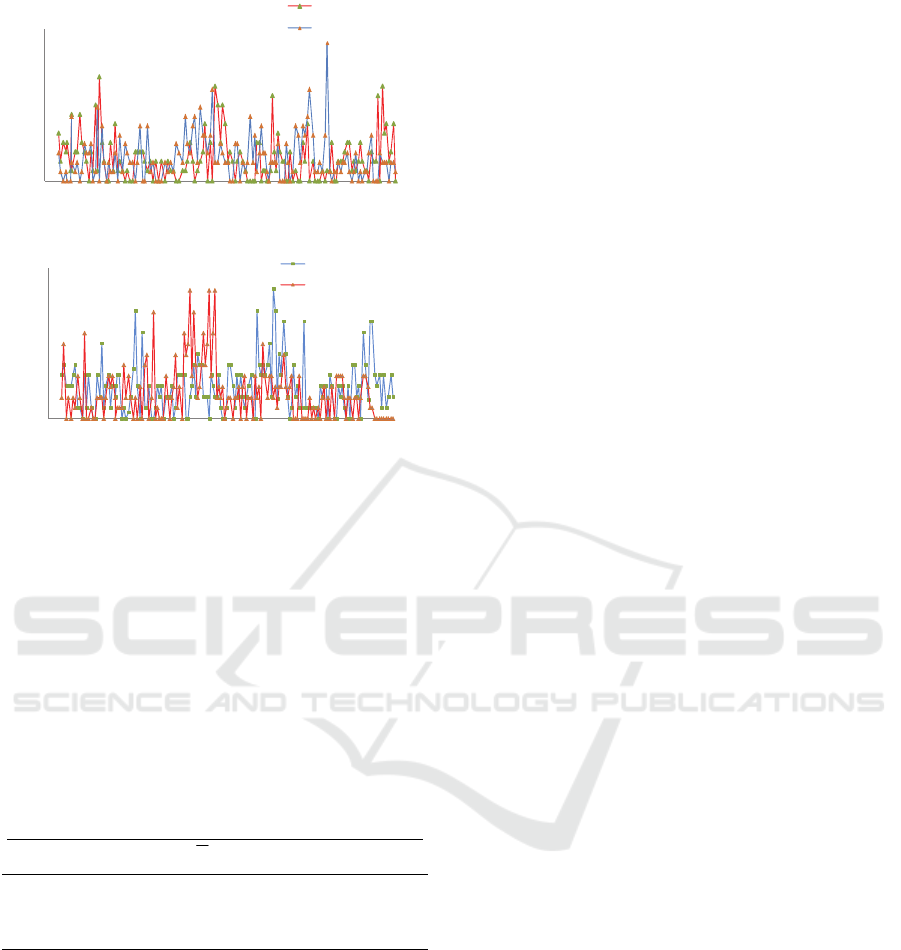
Fig.5 and Fig.6 are relative error sequences of
predicted data versus experimental data in Y and Z
direction, respectively. According to the figures,
most of the relative error are concentrated less than
20 percent. Obviously, the relative error sequence of
Y direction is more concentrated than that of Z
direction. The cause of the phenomenon is that the
original data of Z direction are relatively smaller
than that of Y direction.
Grey Prediction on Cage Dynamic Behavior of Cylindrical Roller Bearing
459
Grey Prediction on Cage Dynamic Behavior of Cylindrical Roller Bearing
459

0
5
10
15
20
25
30
0 200 400 600 800 100 0
relative error /%
ms
Ydirectionat+Xside
Ydirectionat‐Xside
Figure 5: Relative error sequence of Y direction.
0
5
10
15
20
25
30
35
40
0 200 400 600 800 100 0
relative error /%
ms
Zdirectionat+Xside
Zdirectionat‐Xside
Figure 6: Relative error sequence of Z direction.
5 CONCLUSIONS
The posteriori error test results are listed as Tab.3.
According to the results listed in the Tab, the
variance ratio C of four original data serious are
0.52, 0.19, 0.48 and 0.44, receptively. Then the
precision grade can be defined as qualified based on
the precision scale listed in Tab.1. Factually, the
small error probability P is set as 0.85 in prediction
process. The posteriori error test results illustrate
that the reliability of predicted data.
Table 3: Posteriori error test results.
S
1
2

S
2
2
C
Y +X side 0.00103 0.000172 0.000275 0.49
-X side 0.00078 0.000316 0.000028 0.19
Z +X side 0.00149 0.001033 0.000353 0.48
-X side 0.00112 0.000126 0.000213 0.44
ACKNOWLEDGEMENTS
The project is supported by National Natural Science
Foundation of China (Grant No.51475144) and the
Foundation of Innovation and Research Team of
Science and Technology in Universities in Henan
Province (Grant No. 13IRTSTHN025). The
experiment data of this paper originates in the
published paper of NTN technical review. The
authors thank for the provider of the data as well.
REFERENCES
Moore, R., Lopes, J., 1999. Paper templates. In
TEMPLATE’06, 1st International Conference on
Template Production. SCITEPRESS.
Smith, J., 1998. The book, The publishing company.
London, 2
nd
edition.
Houpert, L., 2010. CAGEDYN: A contribution to roller
bearing dynamic calculations. Part III: Experimental
validation, ASME Tribology Transactions, vol. 53, pp.
848–859,
Harsha, S. P., 2006. Nonlinear dynamic analysis of rolling
element bearings due to cage run-out and number of
balls, Journal of Sound and Vibration, 289, pp. 360–
381.
Xia, X. T., Lv, T. M, 2012. Dynamic prediction model for
rolling bearing friction torque using grey bootstrap
fusion method and chaos theory. Advanced Materials
Research, 443-444, pp.87-96.
ISME 2015 - Information Science and Management Engineering III
460
ISME 2015 - International Conference on Information System and Management Engineering
460