Quantitative Estimation of Long-living Fluorescent Molecules from

Temporal Fluorescence Intensity Data Corrupted by Nonzero-mean

Noise

Sofia Startceva, Jerome G. Chandraseelan, Ari Visa and Andre S. Ribeiro

Department of Signal Processing, Tampere University of Technology, Tampere, Finland

Keywords: Fluorescence-tagged RNA Quantification, Single-molecule Time-lapse Microscopy, Biosignal Processing.

Abstract: We present a new quantitative method of estimation of fluorescent molecule numbers from time-lapse,

single-cell, fluorescence microscopy data. Its main aim is to eradicate backward propagation of noise, which

is present in previous methods. The method is first validated using Monte Carlo simulations. These tests

show that when the time-lapse data are corrupted with negative noise, the method obtains significantly more

precise results than current techniques. The applicability of the method is demonstrated on novel time-lapse,

single-cell measurements of fluorescently tagged ribonucleic acid (RNA) molecules. Interestingly, we find

that the intervals inferred by the new method have the same mean but reduced variability when compared to

the previously existing method, which, in accordance to human observers, is a more accurate estimation.

1 INTRODUCTION

Gene expression is a complex, multi-step process

(McClure, 1985; Lutz and Bujard, 1997; DeHaseth

et al., 1998; Yarchuk et al., 1992; Wen et al., 2008;

Zhang et al., 2014). In addition, the underlying steps

of this process are stochastic in nature, generating a

variability in RNA and protein numbers that mostly

explains the phenotypic diversity of monoclonal cell

populations (McAdams and Arkin, 1997; Elowitz et

al., 2002; Rao et al., 2002; Raser and O’Shea, 2005).

To study this process, specialised techniques in

molecular biology (Golding and Cox, 2004; Yu et

al., 2006), microscopy (Rutter et al., 1998;

Chowdhury et al., 2012), image analysis

(Chowdhury et al. 2013; Häkkinen et al., 2013),

computational biology (Zhu et al., 2007) and signal

processing (Häkkinen and Ribeiro, 2014) were

developed.

Methods of signal processing should consider the

characteristics of the underlying processes. For

example, in the RNA tracking technique based on

MS2-GFP tagging, the MS2-GFP proteins

(composed of the bacteriophage MS2 coat protein

fused to the GFPmut3 protein (Golding et al., 2005))

bind to multiple MS2 binding sites of the target

RNA soon after its production, and once formed,

those RNA-MS2-GFP complexes remain in a cell

for the duration of the experiment (Golding and Cox,

2004; Muthukrishnan et al., 2012). Thus, in this

case, when estimating the numbers of target RNAs,

any signal reduction can be classified as noise.

Since complexes can co-localize, the number of

target RNAs in each cell is estimated from the total

fluorescence of the complexes at a given moment

(Golding and Cox, 2004; Kandhavelu et al., 2012;

Häkkinen and Ribeiro, 2014). However, the signal

can be disrupted (i.e. subject to nonzero-mean

noise), which hampers an exact determination of

fluorescent molecules’ numbers. That is, though the

number of RNA-MS2-GFP complexes in a cell is

considered as a monotonic non-decreasing function

during the experiment (Muthukrishnan et al., 2012),

the total fluorescence intensity of the tagged RNA

molecules can decrease, transiently or permanently,

in the course of an experiment. These decreases are

usually caused by the RNA complexes moving away

from the focal plane, or as a result of

photobleaching. While the latter corrupts the data

permanently, the former are isolated events in single

cell time series and usually cause a steep, transient

decrease in the fluorescence intensity of tagged

RNA molecules.

Here, we present a new quantitative method of

estimation of fluorescent molecule numbers from

single-cell fluorescent intensity data obtained by

Startceva S., Chandraseelan J., Visa A. and Ribeiro A.

Quantitative Estimation of Long-living Fluorescent Molecules from Temporal Fluorescence Intensity Data Corrupted by Nonzero-mean Noise.

DOI: 10.5220/0005605900170024

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSIGNALS 2016), pages 17-24

ISBN: 978-989-758-170-0

time-lapse microscopy. The method aims to

eliminate backward noise propagation, caused by

molecules ‘moving out of focus’, which currently is

one of the main sources of noise in the estimation of

the numbers of fluorescent molecules from time-

lapse, live cell images.

2 METHODS

The technique of RNA detection by MS2-GFP

tagging allows observing individual RNA molecules

in live cells, soon after they are transcribed (Golding

et al., 2005). In order to extract information from the

images in an automated fashion, it is necessary to

detect the tagged RNA molecules, which appear as

bright spots in the image. Then, the intensity of the

spots is extracted and summed, so as to obtain the

“total RNA intensity signal” in a cell, at a given

point in time.

This RNA intensity signal from non-degradable

fluorescent tagged RNA molecules contains noise

accumulated through each step of signal registration

(microscope settings, image registration and image

processing). From observation of the data

(Muthukrishnan et al., 2012; Kandhavelu et al.,

2012; Häkkinen et al., 2014), we assume that the

signal behaves as a monotonic non-decreasing

function corrupted with three types of noise:

1. Consistent, normally distributed independent

noise (probability of occurrence 



= 1), with zero

mean and given standard deviation, which is

introduced by imprecisions of the microscope and

detector (Chowdhury et al., 2012; Waters, 2009).

2. Negative noise, which in our measurements

corresponds to fluorescent molecules moving out of

focus and remaining there for a certain amount of

time. Probabilities 



of going out of focus and





of returning to focus depends, e.g., on the type

of fluorescent molecule, temperature, etc.

3. Inconsistent positive noise (low probability of

occurrence, 



<0.01), caused, for instance, by

false-positive detection of fluorescent molecules.

These events are independent from each other, so the

probability of occurring n times is 





, which is

negligible for ≥3. Note that, the limit value of p

is set by empirical observations that these events are

rare.

2.1 Previous Computational Methods

In (Häkkinen and Ribeiro, 2014), a method was

proposed for estimating RNA numbers and

production intervals from temporal data of tagged

RNAs fluorescence intensity in individual cells. This

method, here denominated as a ‘reference method’,

has three steps. First, a monotonically increasing

curve is fitted to the time series, and temporal

information on related samples is extracted. Second,

the intensity of a single fluorescent molecule, or a

‘jump size’, is estimated from the information

obtained at the first step. In the third and final step, a

quantized curve is fit to the time series, given the

parameters, enforcing the quantization to the fit.

From this, the RNA numbers are extracted.

The third step in (Häkkinen and Ribeiro, 2014)

goes as follows. Given the jump size, time series are

fitted quantitatively, and the fit obtained is an

estimation of the number of fluorescent molecules.

For the fits performed throughout the method,

one can use least squares (LSQ) or least absolute

deviations (LD) fitting. The LD was found to be

more robust to signal disruptions.

In order to exploit the characteristics of the

empirical data, this method assumes that all

fluorescent molecules have the same intensity and

that, once formed, they do not degrade before the

end of the measurements (experimental evidence for

this assumption is provided in (Muthukrishnan et al.,

2012)). The first assumption is equivalent to

assuming that the jump size is a constant. The

second assumption corresponds to forbidding non-

monotonic behaviour of quantitative estimation of

the molecules over time.

This method fits full time series to a curve in one

step, which aids in eliminating a consistent zero-

mean noise, but also allows a backward propagation

of any inconsistent disruption of the signal. Hence,

although this method fully addresses the problems of

the first and the third types of noise described in the

Methods section, the problem of the second type of

noise is addressed only to a limited extent (a

fluorescent molecule is detectable only if it is in

focus for at least more than 50% of the time series

length).

2.2 Experimental Methods

2.2.1 Cells, Plasmids, Chemicals and Media

For live, single cell, time-lapse measurements of the

RNA production times, the MS2d-GFP tagging

system was used. Fluorescent RNA-MS2d-GFP

complexes were observed in Escherichia coli DH5α-

PRO strain (generously provided by Ido Golding,

University of Illinois, IL). The strain contains a

single copy plasmid (coding for the RNA with 96

MS2d binding sites under the control of the

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

promoter P

lac

) and a high-copy reporter plasmid

coding for MS2d-GFP under the control of the

promoter P

LtetO-1

(Golding and Cox, 2004).

For growth media, we used the following

composition per 100 ml: 1.5 g tryptone, 0.75 g yeast

extract and 1 g NaCl (pH of 7.0). Media components

were purchased from LabM (UK), while antibiotics,

Isopropyl b-D-1-thiogalactopyranoside (IPTG),

arabinose, and anhydrotetracycline (aTc) are from

Sigma-Aldrich (USA).

2.2.2 Cell Growth and Microscopy

Cells from the DH5α-PRO strain, containing the

target and the reporter plasmids, were grown

overnight, diluted into fresh media to an OD

600

0.1 (measured with an Ultraspec 10 cell density

meter), and allowed to grow to an OD

600

of ~0.3. For

the reporter plasmid induction, aTc (100 ng/ml) was

added 1 h before the start of the measurements. For

the target plasmid, IPTG (1mM) was added 10 min

before the start of the measurements. Cells were

pelleted and resuspended into fresh medium. A few

µl of the cells were placed between a coverslip and

an agarose gel pad (2%), containing the respective

inducers, in a thermal imaging chamber (FCS2,

Bioptechs), heated to 37

C. The cells were

visualized using a Nikon Eclipse (Ti-E, Nikon,

Japan) inverted microscope with a C2+ confocal

laser-scanning system using a 100x Apo TIRF

objective. Images were acquired using the Nikon

Nis-Elements software. GFP ﬂuorescence was

measured using a 488 nm argon ion laser (Melles-

Griot) and 514/30 nm emission ﬁlter. Phase contrast

images were acquired with an external phase

contrast system and a Nikon DS-Fi2 camera.

Fluorescence images were acquired every 1 min for

2 hours. Phase-contrast images were acquired every

5 min.

2.2.3 Image Analysis

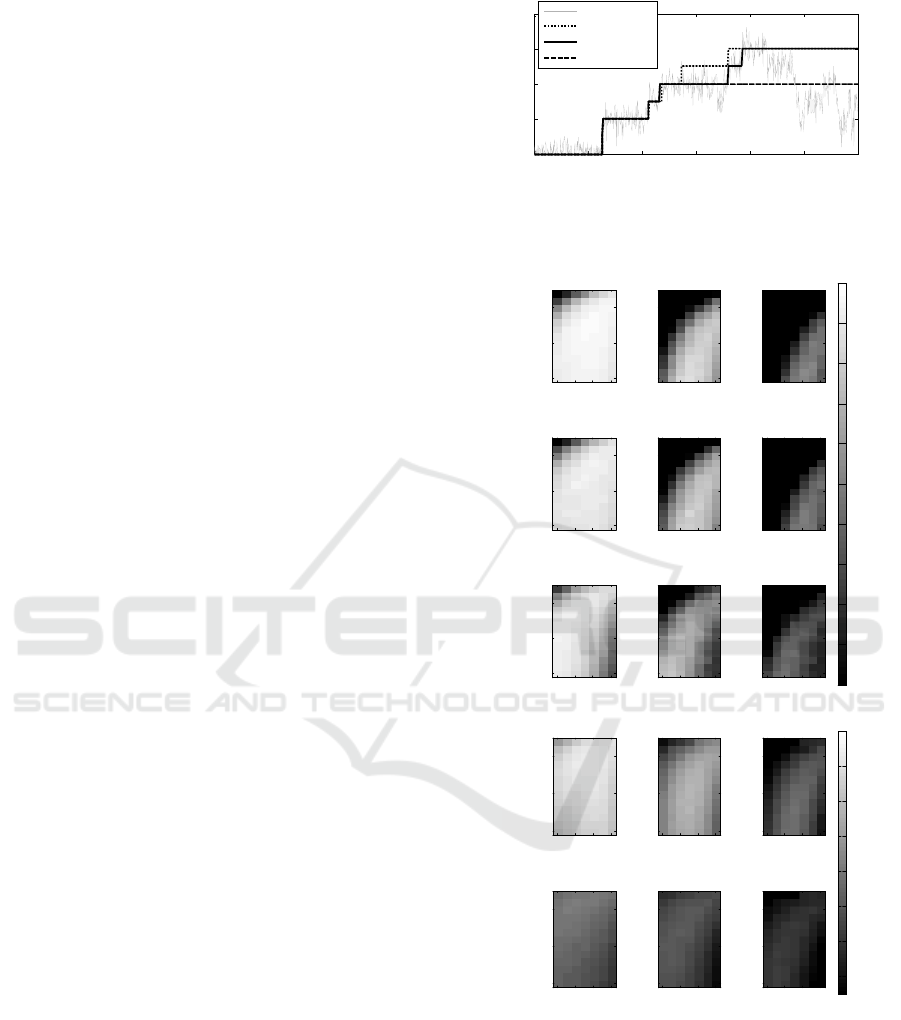
Figure 1. Panel A and B exemplify phase contrast and

confocal images, correspondingly, of the same cells. Panel

C shows masks of those cells and their fluorescent spots.

Cells were detected from phase contrast images as in

(Gupta et al., 2014). First, the images were

temporally aligned using cross-correlation. Next, an

automatic segmentation of the cells was obtained

with MAMLE (Chowdhury et al., 2013). The results

were corrected manually. Cell lineages were

constructed by CellAging (Häkkinen et al., 2013).

Alignment of the phase contrast images with the

confocal images was done by manually selecting 5-7

landmarks in both images, and using thin-plate

spline interpolation for the registration transform.

After the registration, the cell masks were adjusted

to the borders of corresponding cells from the

confocal images based on the fluorescent intensity.

Finally, fluorescent spots and their intensities were

detected from confocal images using a Gaussian

surface-fitting algorithm from (Häkkinen et al.,

2014). Examples of original images and obtained

masks are shown in Figure 1.

3 RESULTS

3.1 Algorithm

Our algorithm for the quantitative estimation of

fluorescent molecules from the data is described in

Figure 2.

3.1.1 Initial Parameters

To obtain the intensity of one fluorescent molecule,

, we combine the first two steps of the ‘reference

method’ in their original form with visual inspection

of the time series of fluorescence intensity. Other

methodologies could be used instead.

To account for positive noise (type 3 noise), the

‘trusted interval’, , is introduced. If an increase in

intensity persists for  frames, then we assume that

this increase is not due to noise. Otherwise, the

assumption that it is positive noise cannot be

rejected.

The choice of the value of  is based on the

standard deviation σ of a consistent noise (type 1).

The optimum value of  rises with the increase of σ

(Figure 4). Also, we found by inspection that, to be

resistant to the type 3 noise,  should not be smaller

than 5 data points.

The parameter  is introduced to account for

deviations in the mean of type 1 noise. The

exploration of the parameter space of the fit

(Figure 4) shows that, for a signal without a

consistent non-zero mean noise,  ≈ 0.25 is an

optimal value. However, the optimal  increases up

to 0.4 in the case of fitting a signal with σ=2.

Quantitative Estimation of Long-living Fluorescent Molecules from Temporal Fluorescence Intensity Data Corrupted by Nonzero-mean

Noise

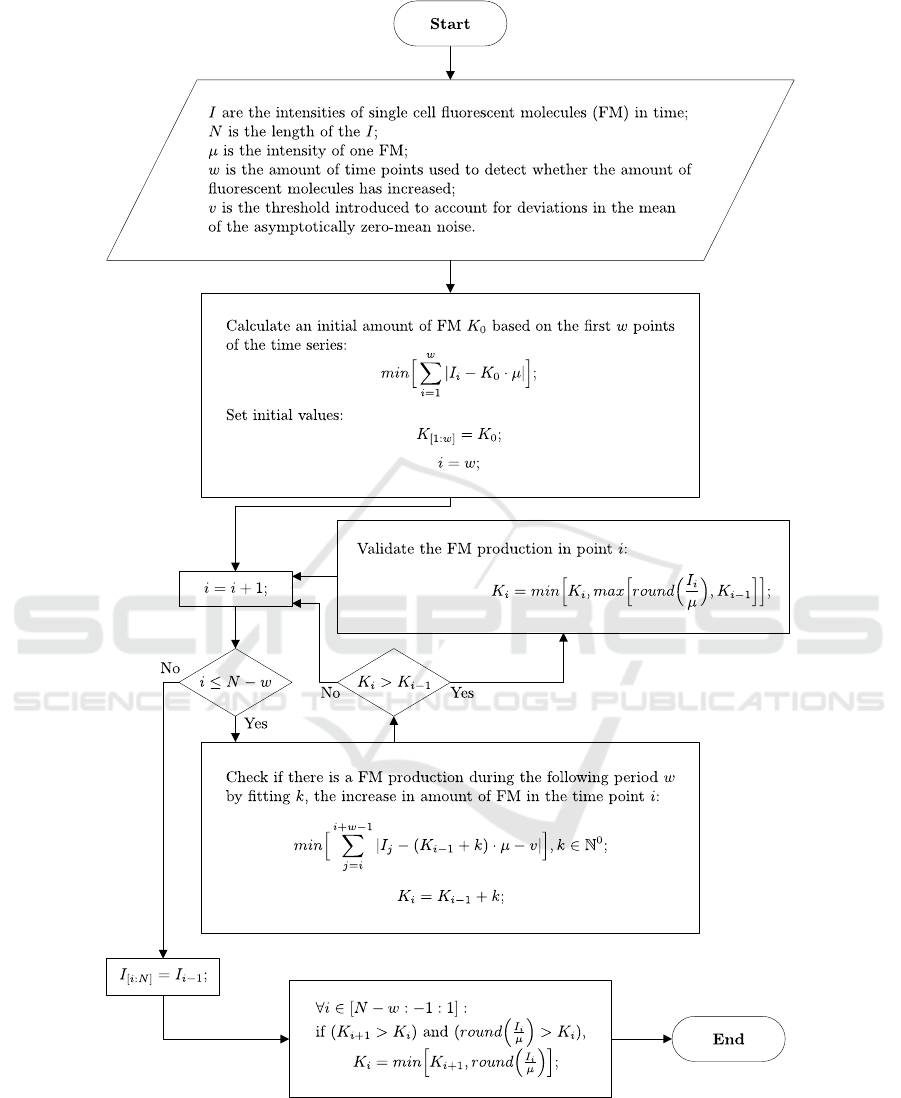
Figure 2: Algorithm used for the quantization of fluorescent molecules.

3.1.2 Computational Procedure

The procedure of the algorithm can be represented

as a set of interval-fitting events. Each interval has

length , the values of each fit at each time point are

a constant proportional to , the fit is performed

using least absolute deviations and, the coefficient of

proportion  of the best fit is an initial estimate of

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

the amount of fluorescent molecules. Given this,

first, we estimate the amount of fluorescent

molecules in the first  time points. For each

following data point 



, where <≤−, the

fit is performed. If 



>



, then the estimated

amount of fluorescent molecules at time point 



the maximum value of the estimated amount



(







⁄)

at 



, and the estimated amount 







Since it is not possible to determine whether any

increase in the signal at the time points [ −  +

1: ] is caused by noise or by the production of

fluorescent molecules, no estimation is performed on

this interval.

Finally, the obtained time series of estimated

amounts of fluorescent molecules  are checked at

each time point  (from  to 1). If

(





>



)

and

((



/) > 



) are true, 



is set to

(



, (



/)). We note that the

production events at these moments were not

detected during the fitting procedure because of the

local disruptions of the signal in subsequent

moments.

3.2 Analysis of in Silico Data

Monte Carlo simulations were performed using a

model of transcription that assumes that RNA

molecules are produced in exponentially distributed

intervals (with mean interval of 15 min

(Muthukrishnan et al., 2012)). The sampling

frequency ƒ used is 10 sec

-1

and 1 min

-1

, for

comparison.

The obtained time series are then corrupted by

adding zero-mean independent and normally

distributed noise. To introduce significant, transient

disruptions of the signal (i.e. to model RNA-MS2d-

GFP complexes going out of focus), we set the RNA

signal to zero at random moments, for a randomly

selected duration. For that, we set the probability

that an RNA goes out of focus to 



=60 min

-1

and the probability of the zeroed RNA to be fully

recovered to 



=20 min

-1

In Figure 3 we exemplify the outcome of

simulating the model for 120 min.

We use this model’s ground truth data to test the

accuracy of the RNA numbers estimation by our

method. To quantify the accuracy, we define it to be

the proportion of time moments where the RNA

numbers in a cell were correctly detected (Häkkinen

and Ribeiro 2014).

First, the parameter space of the proposed model

was investigated in order to detect a combination of

values of  and  that maximize the accuracy.

Figure 3: Simulated data. ƒ=10sec

-1

.  = 0.5. p



60min

-1

and p



=20min

-1

,  = 8,  = 0.25.

Figure 4: Mean accuracy along the parameter space of

and for  = 0.5,  = 1, and  = 2. In panel A, ƒ=

10sec

-1

and in panel B, ƒ=1min

-1

. In both panels, from a-

c: p



=0 min

-1

and p



=0min

-1

; from d-f: p



60min

-1

and p



=20min

-1

; from g-i: 25% time series

points were randomly selected and set to zero. In all sub-

panels of panel A and in sub-panels a-c of panel B, each

accuracy value is a mean of 1000 simulations. In sub

panels d-f of panel B, each accuracy value is a mean of

2500 simulations.

0 20 40 60 80 100 120

time (min)

Intensity (RNAs)

Intensity

RNA

w = 8, v = 0.25

Reference LD

= 0.5

0 0.2 0.4 0.6

= 1

0 0.2 0.4 0.6

= 2

0 0.2 0.4 0.6

= 0.5

0 0.2 0.4 0.6

= 1

0 0.2 0.4 0.6

= 2

0 0.2 0.4 0.6

= 0.5

0 0.2 0.4 0.6

= 1

0 0.2 0.4 0.6

= 2

0 0.2 0.4 0.6

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

= 0.5

0 0.2 0.4 0.6

= 1

0 0.2 0.4 0.6

= 2

0 0.2 0.4 0.6

= 0.5

0 0.2 0.4 0.6

= 1

0 0.2 0.4 0.6

= 2

0 0.2 0.4 0.6

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Quantitative Estimation of Long-living Fluorescent Molecules from Temporal Fluorescence Intensity Data Corrupted by Nonzero-mean

Noise

For that, we performed a set of at least 1000

simulations for each combination of values of , in

the range [0, 0.6], and w, in the range [3, 15] for

 = 0.5, 1, 2 for each of the following sets of

parameter values: a) p



=0 min

-1

, p



=0 min

(ƒ=10 sec

-1

and ƒ=1 min

-1

); b) p



=60 min

, p



=20 min

-1

(ƒ=10 sec

-1

and ƒ=1 min

-1

);

and c) 25% time series points randomly selected and

set to zero (ƒ=10 sec

-1

). Results are shown in

Figure 4.

From Figure 4,  depends on the variation of 

of the consistent noise (namely, as it increases

monotonically with increasing ), whereas 

depends on the mean consistent noise (which

becomes negative due to zeroing 25% of the time

moments). Also, the optimal trusted interval 

suffered only a slight reduction with a sixfold

decrease of the sampling frequency,

ƒ.

In addition, we found that for  = 0, 0.5, 1,

1.5, 2 and ƒ=10 sec

-1

, we obtain 



5, 7, 13, 13, 13, respectively. Meanwhile, for ƒ=1

min

-1

, we obtain 



= 5, 5, 10, 10, 12,

respectively. Finally, we found that the optimal  ≈

0.25.

Figure 5: Mean accuracy of the counting of fluorescent

molecules using a given method (Opt, Avg, or Ref) with a

given noise model (1, 2, or 3) from STD of zero-mean

noise. Panel A: ƒ=10sec

-1

; panel B: ƒ=1min

-1

. Opt is

the proposed method with =



; Avg is the proposed

method with  = 10(panel A) and  = 8(panel B); Ref

is the reference method. In case 1, p



=0min

-1

and



=0min

-1

. In case 2, p



=60min

-1

and p



20min

-1

. In case 3, 25% of the data points are randomly

selected and set to zero. Each accuracy value is a mean of

10000 simulations (using  = 0.2in case 3 and  =

0.25otherwise).

Next, we analysed the simulated data with and

without going-out-of-focus events using the

proposed method and the LD version of the

reference method, and compared their accuracies.

In particular, we measured the accuracy of our

method for  = 0, 0.5, 1, 1.5, 2, along with an

optimal  (‘Opt’ method) as well as with a mean w

(‘Avg’ method), in order to study the impact of this

parameter as a function of . An estimated optimal 

was chosen separately for data with zero-mean noise

and for data with negative-mean noise. Also, we

measured the accuracy of the reference method

(‘Ref’) on the same data, for comparison.

From Figure 5, in general, the proposed method

has higher precision when analysing data with out-

of-focus events (i.e. is more robust to type 2 noise).

For =0.5, its accuracy is improved from 49.1% to

67.6% for ƒ=10 sec

-1

, and from 47.7% to 60.1%

for ƒ=1 min

-1

. However, our method is less robust

to type 1 noise, which is expected because the data is

processed piecewise.

Also from Figure 5, note how the precision is

lowered for mean  versus optimal . This

difference in precision increases with increasing .

Finally, we made use of the in silico data to

assess the timing of the proposed algorithm. For this,

we measured the time required to analyse 10000

simulated time series with ƒ=1 min

-1

,  = 1,





=60 min

-1

, 



=20 min

-1

, and length of

120 min. For w=4, 8, 16 the duration was 16 s, 12 s,

and 10 s respectively (processor Intel Core i5-2400,

3.10GHz), while v does not have a noticeable impact

on the time length of this process.

3.3 Analysis of Empirical Data

We next applied our method to empirical data,

obtained as described in the methods section. This

data was processed using our method and the

reference method, for comparison (Table 1). The

fluorescent RNA complexes have a non-negligible

tendency to go out of focus, which makes it possible

to demonstrate the usefulness of the proposed

method.

Table 1: Comparative analysis of the mean and variability

of the intervals between consecutive RNA production

events obtained by our method (w=8, v = 0.25) and the

reference method. The data was collected from 178 cells.

Method No.

intervals

Mean

interval

Interval

Our method 158 1047 1.15

Ref. method 153 1018 1.43

From the Table 1, the two methods differ in

performance. Namely, while the two methods infer

similar mean intervals between transcription events

(the new method detected 3% more intervals), the

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

of those intervals duration is significantly

smaller when using the new method (19.6%

smaller). Inspection of the data by two expert human

observers indicated that the new method’s detection

process was the more accurate one (see example

Figure 6).

Figure 6: Example intensity series and estimated RNA

numbers with the proposed method (=8,  = 0.25),

and with the reference method (LD version).

4 CONCLUSIONS

Here we proposed a new method for the quantitative

estimation of fluorescent molecules from temporal

intensity microscopy data. This method was

developed to handle transient, nonzero-mean noise

in the data, i.e. it aims to cope with temporary

absences of fluorescent molecules from the focal

plane in time-lapse microscopy measurements. This

is particularly important in studies requiring a

consistent tracking of tagged molecules, such as

studies of, e.g., chemotaxis mechanisms which rely

on chemoreceptor clusters (Sourjik and Berg, 2004;

Wadhams and Armitage, 2004; Parkinson et al.,

2005; Kentner and Sourjik, 2006) and protein

aggregates’ accumulation, which is associated with

cellular aging processes (Maisonneuve et al., 2008;

Tyedmers et al., 2010; Winkler et al., 2010; Lindner

et al., 2008; Gupta et al., 2014; Lloyd-Price et al.,

2012).

We validated our method by tests on in silico

data. Next, we applied it to empirical data to show

that its results can differ from those of the previous

method. By inspection, we found, as expected, that

the reason why the results of the two methods differ

is the enhanced robustness of our method to

‘negative’, inconsistent noise. Another reason is its

weaker robustness to consistent, type 1 noise.

The causes of the two main differences are that,

in the new method: i) previous values of a tagged

RNA intensity confine the next ones into boundaries

defined by the known properties of the signal. The

main benefit of this is that it restricts backward

propagation of inconsistent noise, which results in

more precise results when p



>0; ii) the

stepwise analysis of the signal hampers the removal

of consistent zero-mean noise.

We expect our method to be of use to a broad

range of time-lapse microscopy measurements

making use of fluorescence molecules in live cells,

particular when the phenomenon of moving out of

the focus plane is common for those molecules.

ACKNOWLEDGEMENTS

Work supported by TUT’s Graduate School (SS)

and Academy of Finland (257603, ASR). The

funders had no role in study design, data collection

and analysis, decision to publish, or preparation of

the manuscript.

REFERENCES

Chowdhury, S. et al., 2012. An interacting multiple model

filter-based autofocus strategy for confocal time-lapse

microscopy. J.Microscopy, 245, pp.265–75.

Chowdhury, S. et al., 2013. Cell segmentation by multi-

resolution analysis and maximum likelihood

estimation (MAMLE). BMC Bioinformatics, 14 (Suppl

10), p.S8.

DeHaseth, P.L., Zupancic, M.L. and Record, M.T., 1998.

RNA polymerase-promoter interactions: The comings

and goings of RNA polymerase. J Bacteriology,

180(12), pp.3019–25.

Elowitz, M.B. et al., 2002. Stochastic gene expression in a

single cell. Science, 297(5584), pp.1183–6.

Golding, I. et al., 2005. Real-time kinetics of gene activity

in individual bacteria. Cell, 123(6), pp.1025–36.

Golding, I. and Cox, E.C., 2004. RNA dynamics in live

Escherichia coli cells. Proc. of the National Academy

of Sciences of the USA, 101(31), pp.11310–5.

Gupta, A., Lloyd-Price, J., Neeli-Venkata, R., et al., 2014.

In Vivo Kinetics of Segregation and Polar Retention

of MS2-GFP-RNA Complexes in Escherichia coli.

Biophysical J., 106(9), pp.1928–37.

Gupta, A., Lloyd-Price, J., Oliveira, S.M.D., et al., 2014.

Robustness of the division symmetry in Escherichia

coli and functional consequences of symmetry

breaking. Physical Biology, 11(6), p.066005.

Häkkinen, A. and Ribeiro, A.S., 2014. Estimation of GFP-

tagged RNA numbers from temporal fluorescence

intensity data. Bioinformatics, 31(1), pp.69–75.

Häkkinen, A. et al., 2013. CellAging: A tool to study

segregation and partitioning in division in cell lineages

of Escherichia coli. Bioinformatics, 29(13), pp.1708–9.

Häkkinen, A. et al., 2014. Estimation of fluorescence-

tagged RNA numbers from spot intensities.

Bioinformatics, 30(8), pp.1146–53.

Kandhavelu, M. et al., 2012. Single-molecule dynamics of

transcription of the lar promoter. Physical Biology,

9(2), p.026004.

0 20 40 60 80 100 120

time

(

min

)

Intensity (RNAs)

Intensity

w = 8, v = 0.25

Reference LD

Quantitative Estimation of Long-living Fluorescent Molecules from Temporal Fluorescence Intensity Data Corrupted by Nonzero-mean

Noise

Kentner, D. and Sourjik, V., 2006. Spatial organization of

the bacterial chemotaxis system. Current Opinion in

Microbiology, 9(6), pp.619–24.

Lindner, A.B. et al., 2008. Asymmetric segregation of

protein aggregates is associated with cellular aging

and rejuvenation. Proc. of the National Academy of

Sciences of the USA, 105(8), pp.3076–81.

Lloyd-Price, J. et al., 2012. Asymmetric disposal of

individual protein aggregates in Escherichia coli, one

aggregate at a time. J.Bacteriology, 194(7), pp.1747–

52.

Lutz, R. and Bujard, H., 1997. Independent and tight

regulation of transcriptional units in Escherichia coli

via the LacR/O, the TetR/O and AraC/I1-I2 regulatory

elements. Nucleic Acids Research, 25(6), pp.1203–10.

Maisonneuve, E., Ezraty, B. and Dukan, S., 2008. Protein

aggregates: An aging factor involved in cell death.

J.Bacteriology, 190(18), pp.6070–5.

McAdams, H.H. and Arkin, A., 1997. Stochastic

mechanisms in gene expression. Proc. of the National

Academy of Sciences of the USA, 94(3), pp.814–9.

McClure, W.R., 1985. Mechanism and control of

transcription initiation in prokaryotes. Ann. Rev. of

Biochemistry, 54, pp.171–204.

Muthukrishnan, A.-B. et al., 2012. Dynamics of

transcription driven by the tetA promoter, one event at

a time, in live Escherichia coli cells. Nucleic Acids

Research, 40(17), pp.8472–83.

Parkinson, J.S., Ames, P. and Studdert, C.A., 2005.

Collaborative signaling by bacterial chemoreceptors.

Current opinion in microbiology, 8(2), pp.116–21.

Rao, C. V, Wolf, D.M. and Arkin, A.P., 2002. Control,

exploitation and tolerance of intracellular noise.

Nature, 420(6912), pp.231–7.

Raser, J.M. and O’Shea, E.K., 2005. Noise in gene

expression: origins, consequences, and control.

Science, 309(5743), pp.2010–3.

Rutter, G.A. et al., 1998. Real-time imaging of gene

expression in single living cells. Chemistry and

biology, 5(11), pp.R285–90.

Sourjik, V. and Berg, H.C., 2004. Functional interactions

between receptors in bacterial chemotaxis. Nature,

428(March), pp.1–4.

Tyedmers, J., Mogk, A. and Bukau, B., 2010. Cellular

strategies for controlling protein aggregation. Nature

rev. Mol. cell biology, 11(11), pp.777–88.

Wadhams, G.H. and Armitage, J.P., 2004. Making sense

of it all: bacterial chemotaxis. Nature rev. Mol. Cell

Biology., 5(12), pp.1024–37.

Waters, J.C., 2009. Accuracy and precision in quantitative

fluorescence microscopy. J.Cell Biology, 185(7),

pp.1135–48.

Wen, J.-D. et al., 2008. Following translation by single

ribosomes one codon at a time. Nature, 452(7187),

pp.598–603.

Winkler, J. et al., 2010. Quantitative and spatio-temporal

features of protein aggregation in Escherichia coli and

consequences on protein quality control and cellular

ageing. The EMBO J., 29(5), pp.910–23.

Yarchuk, O., Guillerez, J. and Dreyfus, M., 1992.

Interdependence of Translation, Transcription

Degradation in the ZacZ Gene and mRNA.

J.Molecular Biology, pp.581–96.

Yu, J. et al., 2006. Probing gene expression in live cells,

one protein molecule at a time. Science, 311(5767),

pp.1600–03.

Zhang, Z. et al., 2014. Single-molecule tracking of the

transcription cycle by sub-second RNA detection.

eLife, 2014(3), pp.1–20.

Zhu, R. et al., 2007. Studying genetic regulatory networks

at the molecular level: Delayed reaction stochastic

models. J. Theoretical Biology, 246(4), pp.725–45.

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing