Evaluation and Optimization of Adaptive Cruise Control Policies Via
Numerical Simulations
Clement U. Mba
1
and Carlo Novara
2
1
Department of Mechanical and Aerospace Engineering, Politecnico di Torino, Corso Duca degli Abruzzi, 24, Torino, Italy
2
Department of Control and Computer Engineering, Politecnico di Torino, Corso Duca degli Abruzzi, 24, Torino, Italy
Keywords:
Adaptive Cruise Control, Test Simulation, Performance Optimization.
Abstract:
Adaptive Cruise Control (ACC) makes the driving experience safer and more pleasurable. Several appealing
ACC policies have been introduced so far. However, it is difficult in general to understand which is the actual
performance that can be guaranteed on a real vehicle. Another relevant issue is that no systematic methods
can be found for the optimization of a control policy performance. The first aim of this paper is to compare
different ACC policies by means of extensive simulations, considering different realistic road scenarios. This
kind of study is important to analyze which policies can be more effective in view of their implementation on
real vehicles. The second aim is to develop an optimization method based on a multi-objective Pareto criterion,
finalized at designing high-performance policies. The method is tested by means of extensive simulations.
1 INTRODUCTION
Driving can be defined as a set of operations aimed at
controlling a motor vehicle, where control is typically
performed by a human driver. However, the human
driver behavior may tend sometimes to cause undesir-
able vehicle behaviors. In modern vehicles, to avoid
or prevent these kinds of behaviors, control is usu-
ally done by the human driver with the help of some
Driver Assistance Systems, one of the most important
of which is the Cruise Control.
Cruise Control (CC) has the task of maintaining
the vehicle speed at a desired value. However, a draw-
back of CC is that it cannot vary the speed of the
vehicle: whenever a vehicle in front of the vehicle
equipped with CC is traveling slower than the latter,
the driver has to step on the brakes in order to de-
activate the Cruise Control and step on the acceler-
ator when the preceding vehicle speeds up, (Howard,
2013). As a result, Cruise Control has to be reset from
time to time. This drawback is overcome by the more
advanced Adaptive Cruise Control (ACC), which is
able to adjust the speed of the vehicle, depending
on various factors influencing it without manual in-
tervention from the driver, (Howard, 2013; Shakouri
et al., 2012, 2014). Some of them, like the “stop and
go”, can bring the vehicle to a stop and start it mov-
ing, (Shakouri et al., 2012, 2014).
In general, the design of an ACC begins with
an ACC policy. Different ACC policies have been
proposed: Constant Time Gap (CTG), Constant Dis-
tance, Constant acceptance, Constant Stability and
Constant safety factor (Xiao et al., 2010). ACC poli-
cies specify the desired steady state distance between
two vehicles in succession. Note that ACC policies
can be either autonomous, (Rajamani, 2012), coop-
erative, (Schakel et al., 2010; Oncu et al., 2010) or
a combination of both, (Swaroop, 1995). Introducing
and maintaining continuous inter-vehicular communi-
cation, which is the main feature of cooperative poli-
cies causes network effects that can undermine the
performance of the ACC (Oncu et al., 2010). More-
over, maintaining continuous inter-vehicular commu-
nication is costly (Yanakiev et al., 1995, 1998). Thus,
the autonomous operation seems like the most pre-
ferred choice at present, and it is the area of focus in
this paper.
The performance of an ACC system is based on
the particular control policy that it employs. The ba-
sic control policies are the Constant Spacing Policy
(CSP), Constant Time Gap (CTG) and Variable Time
Gap (VTG). All the other policies are usually vari-
ants of these basic policies. However, even though all
these policies are appealing from a methodological
point of view, it is difficult in general to understand
which is the actual performance that can be guaran-
teed on a real vehicle. Another relevant issue is that,
to the best of our knowledge, no systematic methods
Mba, C. and Novara, C.
Evaluation and Optimization of Adaptive Cruise Control Policies Via Numerical Simulations.
In Proceedings of the International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2016), pages 13-19
ISBN: 978-989-758-185-4
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
13

can be found for the optimization of the control policy
performance.
In this perspective, the main contributions of the
paper are two. First, the control policies employed by
the “standard” ACC systems are compared by means
of extensive simulations, considering different realis-
tic road scenarios. This kind of study is important to
understand which control policies and, more in gen-
eral, which control approaches can be more effec-
tive in view of their implementation on real vehicles.
Second, an optimization strategy based on a multi-
objective Pareto criterion is proposed, finalized at de-
signing high-performance control policies. The strat-
egy is tested by means of extensive simulations, in-
volving different realistic road scenarios. These simu-
lations show that the method allows the design of con-
trol policies able to perform significantly better with
respect to the “standard” policies, in terms of safety
and fuel consumption.
2 VEHICLE MODEL AND
CONTROL POLICIES
In this section, we introduce the vehicle and control
models that will be used in the simulations, first to
compare the “standard” ACC systems, then to test our
optimal control policy design method.
The following assumptions were made:
• All vehicles are identical and move in a straight
line.
• Before the maneuver of the lead vehicle, all the
vehicles were moving at the same steady state
speed.
• The lead vehicle takes a finite amount of time to
perform a maneuver prior to reaching steady state
speed.
The longitudinal dynamics of each vehicle (plant)
can be approximated by the following model (see (Ra-
jamani, 2012; Santhanakrishnan et al., 2003; Swaroop
et al., 1994)):
τ
...
p
+ ¨p = u (1)
where p is the vehicle longitudinal position, u repre-
sents a “desired” longitudinal acceleration and τ is the
vehicle time constant.
The desired acceleration u is the control input,
which can be used to improve the vehicle perfor-
mance in terms of safety, comfort and fuel consump-
tion. This task can be accomplished by a proper con-
trol policy, as shown schematically in Fig. 1, where
the block “Vehicle” is a dynamic system described
by (1) and ε is the spacing error to be defined sub-
sequently.
Usually, the control policies should satisfy string
stability requirements in order to give a good perfor-
mance. String stability is defined as stability with re-
spect to the spacing between vehicles. It ensures that
the spacing error, defined as the difference between
the actual and desired spacing, do not get larger as it
propagates upstream in a string of Adaptive Cruise
Control vehicles using the same control law (Raja-
mani, 2012; Santhanakrishnan et al., 2003; Swaroop,
1995; Swaroop et al., 1994; Yanakiev et al., 1998;
Chi-Ying et al., 1999). The CSP policy requires inter-
vehicular communication if string stability is to be
guaranteed (Swaroop et al., 1998; Yanakiev et al.,
1998), while the CTG and VTG policies overcome
this limitation (Yanakiev et al., 1995; Swaroop et al.,
1994; Yanakiev et al., 1998). Since we are only con-
sidering the autonomous operation, our tests are con-
ducted only on the CTG and VTG policies.
The CTG policy is defined by the control law
u = −
( ˙p − ˙p
f
+ λε)
h
(2)
ε = p −p
f
+ L
des
where p and p
f
are the positions of a vehicle and
the preceding vehicle respectively, and ε is the devi-
ation from the desired spacing, otherwise known as
the spacing error, (Rajamani, 2012; Santhanakrishnan
et al., 2003; Swaroop et al., 1994; Zhao et al., 2009).
λ, L
des
and h are design parameters, to be chosen
in order to obtain the desired longitudinal dynamics
performance. λ is a control gain, L
des
is the desired
spacing between the vehicles and h is called the time
gap (it represents the time distance between the two
vehicles).
Combining the vehicle equation (1) with the con-
trol equations (2), we obtain an Linear Time Invariant
(LTI) system, with input p
f
and output y = ε. Note
that, on a vehicle equipped with an ACC systems, p
f
is typically measured by a radar.
The VTG has several variants (Zhou et al., 2004;
Santhanakrishnan et al., 2003; Yanakiev et al., 1995;
Zhao et al., 2009; Wang et al., 2004, 2002; Zhou et al.,
2005), which are similar to each other. The Nonlin-
ear Range Policy (NRP) (Zhou et al., 2004, 2005) is
considered here because of its simple structure. This
policy is defined by the control law
u = (1 −
τk
h
−
τλk
h
2
h
2
k
) ¨p +(
τk
h
2
) ˙p
f
− ˙p (3)
where k is a design parameter, called the scaling factor
(Zhou et al., 2004, 2005).
As for the VTG policy, combining the vehicle
equation (1) with the control equations (3), we obtain
an LTI system, with input p
f
and output y = ε.
VEHITS 2016 - International Conference on Vehicle Technology and Intelligent Transport Systems
14

Figure 1: Adaptive Cruise Control structure.
3 ACC POLICIES COMPARISON
The two ACC policies described in Section 2 are
tested considering three different scenarios:
Scenario 1. Constant Number of Vehicles Travel-
ing in a Line
In this scenario, 10 vehicles are traveling in a line
and the lead vehicle makes some critical manoeuvre.
Three kinds of critical manoeuvres are simulated -
Manoeuvre 1: The lead vehicle suddenly increases
its speed; this manoeuvre was obtained simulating u
1
(the input of the leading vehicle) as a filtered posi-
tive step. Manoeuvre 2: The lead vehicle suddenly
increases its speed and then goes back to the original
speed; this manoeuvre was obtained simulating u
1
as
a filtered positive impulse. Manoeuvre 3: The lead
vehicle decelerates continuously; this manoeuvre was
obtained simulating u
1
as a filtered negative ramp.
Scenario 2. Vehicles Joining and Leaving the Line
In this scenario, 10 vehicles are traveling in a line and
one or more vehicles join or leave the line at different
times; this manoeuvre was simulated just by suddenly
increasing or decreasing the number of vehicles in the
line with the gap between the vehicles taken into con-
sideration to prevent collision. Note that this simula-
tion is more challenging than a real situation, where
the process of joining or leaving the line is “more con-
tinuous”. We considered up to 5 vehicles joining or
leaving the line.
Scenario 3. Traffic Flow
In this scenario, 10 vehicles are traveling in a line and
one or more vehicles join or leave the line at differ-
ent times. We considered up to 5 vehicles joining or
leaving the line. As an additional complication, the
line may stop at different times due to the presence
of traffic lights; The stop at the light was obtained
simulating u
1
as a filtered negative ramp that, after a
certain time, becomes constant.
We considered different combinations of the val-
ues of the parameters characterising the vehicle model
and the control policies. In particular, the following
parameter ranges were assumed:
τ ∈ [0.5,0.95] s
λ ∈ [0.4,2]
h ∈ [0.1,2] s
k ∈ [2, 15]
L
des
= 40 m.
For each manoeuvre of scenario 1 and for each pa-
rameter combination, we performed one simulation.
This simulation was long enough to reach steady-state
conditions. For each of scenarios 2 and 3 and for each
parameter combination, we performed a sufficiently
long simulation, in order to capture all relevant situ-
ations that can occur in a real road scenario. In par-
ticular, the duration of the simulated road scenarios
was about 107 hours, corresponding to about 4 hours
of Matlab run time. The simulations were done using
Matlab R2014a and its simulink environment.
To evaluate the performance of an ACC control
policy, we considered the following indexes:
• Recovery Time: The recovery time of a vehicle is
defined
T
R
= T
ss
−T
c
where T
c
is the time at which a critical event oc-
curs (e.g., a critical manoeuvre, a vehicle joining
or leaving the line, or a stop at the light) and T
ss
is
the 2% settling time (that is, the time after which
the system output is always within an interval with
center at the steady-state value of the output and
amplitude 2% of this value).
• Input Signal Root Mean Square Value:
RMS
u
= ||˜u||/
√
N (4)
where ˜u is the (discrete-time) command input sig-
nal of a vehicle acquired from the simulation, ||.||
is the vector 2-norm and N is the length of ˜u.
• Output Signal Root Mean Square Value:
RMS
y
= ||˜y||/
√
N (5)
where ˜y is the acquired (discrete-time) output sig-
nal of a vehicle.
The recovery time measures the capability of the
control policy to promptly bring the vehicle back to
its “normal” operation conditions. RMS
y
essentially
measures the mean deviation of the output from the
desired value (hence, it is also an indirect measure
of the recovery time). RMS
u
is related to the energy
spent by the control policy in order to obtain the de-
sired performance.
Tables 1-6 show the performance indexes obtained
in the simulations, averaged over all the vehicles com-
posing the line, all the critical events (i.e., vehicles
joining and leaving the line and stops at the lights)
Evaluation and Optimization of Adaptive Cruise Control Policies Via Numerical Simulations
15

and all the parameter combinations. The averages are
indicated with a bar. In Figures 2-6, we can observe
the performance indexes obtained in the simulations,
averaged over all the vehicles composing the line and
all the critical events.
Tables 1, 2 and 3 show that the NRP generally
recovers faster when subjected to critical conditions,
involving also lower values of
¯
RMS
y
. However, the
required command activity, measured by
¯
RMS
u
, is
higher. Similar results are shown by Tables 4, 5 and
6.
Given that τ ≥ 0.5 and λ = 0.4, the NRP is more
flexible than the CTG, in the sense that h can be varied
from 0.1 to more than 1.8 without the spacing errors
getting larger as they propagate upstream in vehicles
using NRP. When h = 0.1, for the NRP the recovery
time as well as the
¯
RMS
y
value is “small”, with a high
Table 1: Scenario 1, Manoeuvre 1. Average performance
indexes.
Strategy
¯
T
R
[s]
¯
RMS
u
¯
RMS
y
CTG 33.14 12.508 1.1199
NRP 4.5 14.7154 0.1833
Table 2: Scenario 1, Manoeuvre 2. Average performance
indexes.
Strategy
¯
T
R
[s]
¯
RMS
u
¯
RMS
y
CTG 36.7 0.0228 0.0286
NRP 5.14 0.0820 0.0237
Table 3: Scenario 1, Manoeuvre 3. Average performance
indexes.
Strategy
¯
T
R
[s]
¯
RMS
u
¯
RMS
y
CTG 6.7 35.3265 1.5331
NRP 0.55 45.1805 0.0996
Table 4: Scenario 2, Vehicles joining. Average performance
indexes.
Strategy
¯
RMS
u
¯
RMS
y
CTG 111.7 6.9109
NRP 115.3 5.8677
Table 5: Scenario 2, Vehicles leaving. Average performance
indexes.
Strategy
¯
RMS
u
¯
RMS
y
CTG 109.6 7.1459
NRP 114 6.0608
Table 6: Scenario 3. Average performance indexes.
Strategy
¯
RMS
u
¯
RMS
y
CTG 436 5.608
NRP 441.7 4.191
value of
¯
RMS
u
on the command input activity.
The average recovery time increases a little for ve-
hicles using the NRP as τ gets higher. In the case of
the CTG, the average recovery time increases consid-
erably as τ gets higher. Accordingly, it can be said
that higher values of τ for each of the vehicles do not
have as much influence on vehicles using the NRP as
they do on vehicles that use the CTG. This is most
likely to be a result of the high value of h that is re-
quired in the CTG when τ>0.5, to prevent the spacing
errors from getting larger as they propagate upstream.
The simulation results obtained from scenario 2,
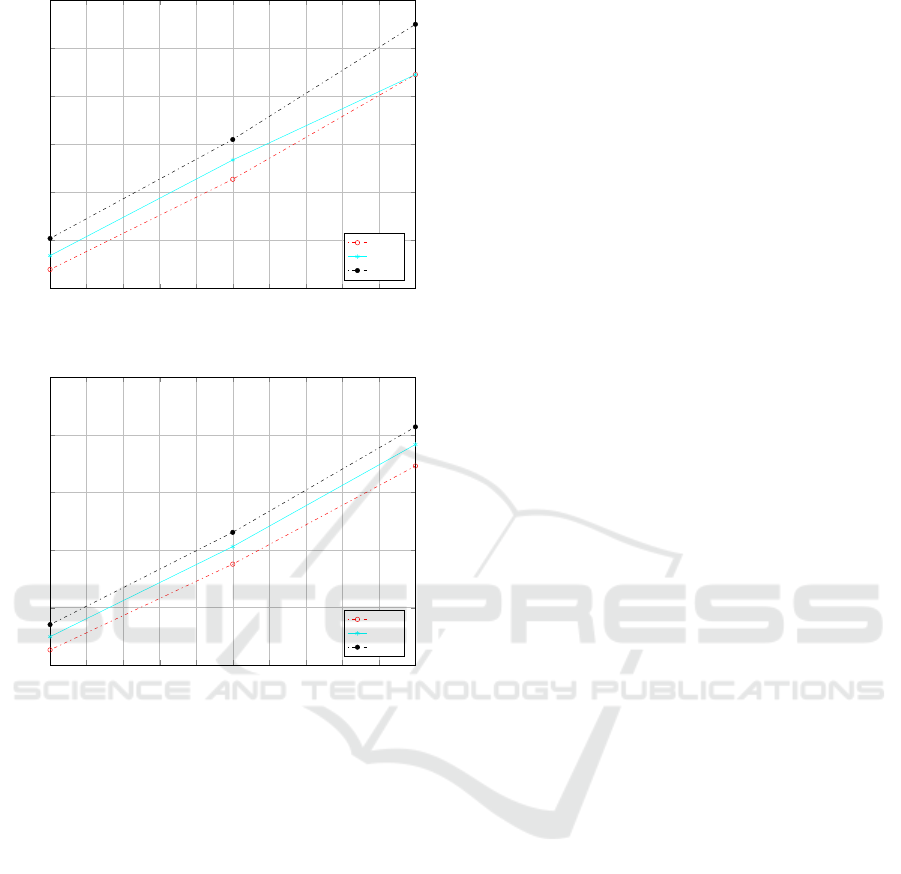
as shown in Figures 2 and 3, and scenario 3, as shown
in Figures 4 and 5, show that the NRP has lower
¯
RMS
y
than the CTG for the same values of h and τ. The two
lines with the same h in Figures 2 and 3 correspond
to the vehicles either joining or leaving the line. It
should also be noted that similar results are obtained
when τ is different for each vehicle in the stream.
Low values of the time gap as well as low values
of
¯
RMS
u
are desirable but these act in contrast to each
other. As stated earlier, lower values of the time gap
1 1.5 2 2.5 3 3.5 4 4.5 5
5.5
6
6.5
7
7.5
8
8.5
9
Number of vehicles joining/leaving the line
¯
RMS
y
h=2.0
h=1.9
h=1.8
h=2.0
h=1.9
h=1.8
Figure 2: Scenario 2 (CTG with τ = 0.5s, λ = 0.4).
1 1.5 2 2.5 3 3.5 4 4.5 5
4.5
5
5.5
6
6.5
7
7.5
Number of vehicles joining/leaving the line
¯
RMS
y
h=2.0
h=1.9
h=1.8
h=2.0
h=1.9
h=1.8
Figure 3: Scenario 2 (NRP with τ = 0.5s, λ = 0.4, k = 4).
VEHITS 2016 - International Conference on Vehicle Technology and Intelligent Transport Systems
16

1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3
4
4.5
5
5.5
6
6.5
7
Number of vehicles joining/leaving the line
¯
RMS
y
h=2.0
h=1.9
h=1.8
Figure 4: Scenario 3 (CTG with τ = 0.5, λ = 0.4).
1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3
3
3.5
4
4.5
5
5.5
Number of vehicles joining/leaving the line
¯
RMS
y
h=2.0
h=1.9
h=1.8
Figure 5: Scenario 3 (NRP with τ = 0.5, λ = 0.4, k = 4).
require higher command input activity. Indeed,
¯
RMS
u
and
¯
RMS
y
are two contrasting criteria. This is impor-
tant for the NRP, since it can sustain h ∈ [0.1,2]. It is
our deduction that if h remains in a “low value zone”
for instance h ∈ [0.1,0.3] for a long time during driv-
ing, a lot of energy due to control activity might be
expended. A possible way to mitigate this could be
to design the control algorithm in such a way that the
time gap does not exceed a certain amount of time
when it is in the “low value zone”. It is important to
determine the right amount of time. This amount of
time could depend on whether there are vehicles join-
ing or leaving the stream as well as on their number,
or on what the design objective of the car manufac-
turer is (i.e, energy reduction or inter-vehicular space
reduction to increase traffic output).
4 OPTIMIZATION STRATEGY
As discussed in the previous section, in the design of
an ACC system there is a trade-off between two con-
trasting requirements. On the one hand, the ACC sys-
tem must provide a satisfactory performance in terms
of safety and prompt answer to external disturbances.
On the other hand, the ACC system must not require a
too large command activity, which may lead to a high
consumption of fuel and/or electrical power.
To quantify the ACC performance we hereby con-
sider the RMS
y
index defined in (5). To quantify the
command activity we consider the RMS
u
index de-
fined in (4). We would like to minimise both these co-
efficients but clearly this cannot be done, since these
indexes are in contrast with each other. In other
words, we are dealing with a multi-objective opti-
mization problem.
This kind of problems can be efficiently solved
considering a Pareto optimality criterion, (B. Brown-
stein., 1980). Let RMS
y
(C) and RMS
u
(C) be respec-
tively the performance and command activity indexes
of a given ACC controller C. A controller C
1
is said
to dominate another controller C
2
if
RMS
y
(C
1
) ≤ RMS
y
(C
2
) and RMS
u
(C
1
) < RMS
u
(C
2
)
or
RMS
y
(C
1
) < RMS
y
(C
2
) and RMS
u
(C
1
) ≤ RMS
u
(C
2
).
(6)
A controller C
∗
is said Pareto optimal if it is not
dominated by any other one. In other words, no other
controller exists that can be overall better than an opti-
mal controller. If a controller is better than an optimal
one with regard to a single objective (e.g., RMS
u
(C)),
it is certainly worse with respect to the other (e.g.,
RMS
y
(C)). The set of Pareto optimal controllers de-
fine a curve in the performance index space called
Pareto front (see the green line in Fig. 6).
Based on these concepts, the optimization strategy
that we propose is as follows:
• Perform a Monte Carlo simulation, consisting of
N
T
trials.
• In each trial:
– Choose random values of the parameters h, k
and λ (clearly, these values must be reason-
able from a physical point of view). Each pa-
rameter 3-tuple defines a controller C
i
, with
i = 1,...,N
T
.
– For the chosen parameter 3-tuple, perform N
S
simulations considering realistic road scenar-
ios.
– compute the averages
¯
RMS(C
i
)
y
and
¯
RMS(C
i
)
u
of the N
S
values of RMS(C
i
)
y
and RMS(C
i
)
u
.
• Considering that the pairs
(
¯
RMS(C
i
)
y
,
¯
RMS(C
i
)
u
), with i = 1,...,N
T
,
Evaluation and Optimization of Adaptive Cruise Control Policies Via Numerical Simulations
17

define points in the two-dimensional performance
index space, construct the Pareto optimality front,
using (6) to individuate those controllers that are
not dominated.
Note that τ and L
des
are assumed fixed but they
can be included in the optimization process without
significant modifications.
Following this strategy, a Monte Carlo simulation
was performed, consisting of N
T
= 4760. In each
trial, random values of h, k and λ were taken from the
intervals [0.1,2], [2,15] and [0.4,2], respectively (a
uniform distribution was considered for all the three
parameters). The values τ = 0.5 s and L
des
= 40 m
were also assumed. For each random 3-tuple (corre-
sponding to a randomly generated controller), N
S
=
10 simulations were performed considering Scenario
3 (traffic flow with 10 vehicles in a line and 5 vehi-
cles randomly joining or leaving the line). Then, the
performance averages
¯
RMS(C
i
)
y
and
¯
RMS(C
i
)
u
were
computed. Finally, the Pareto optimality front was
constructed.
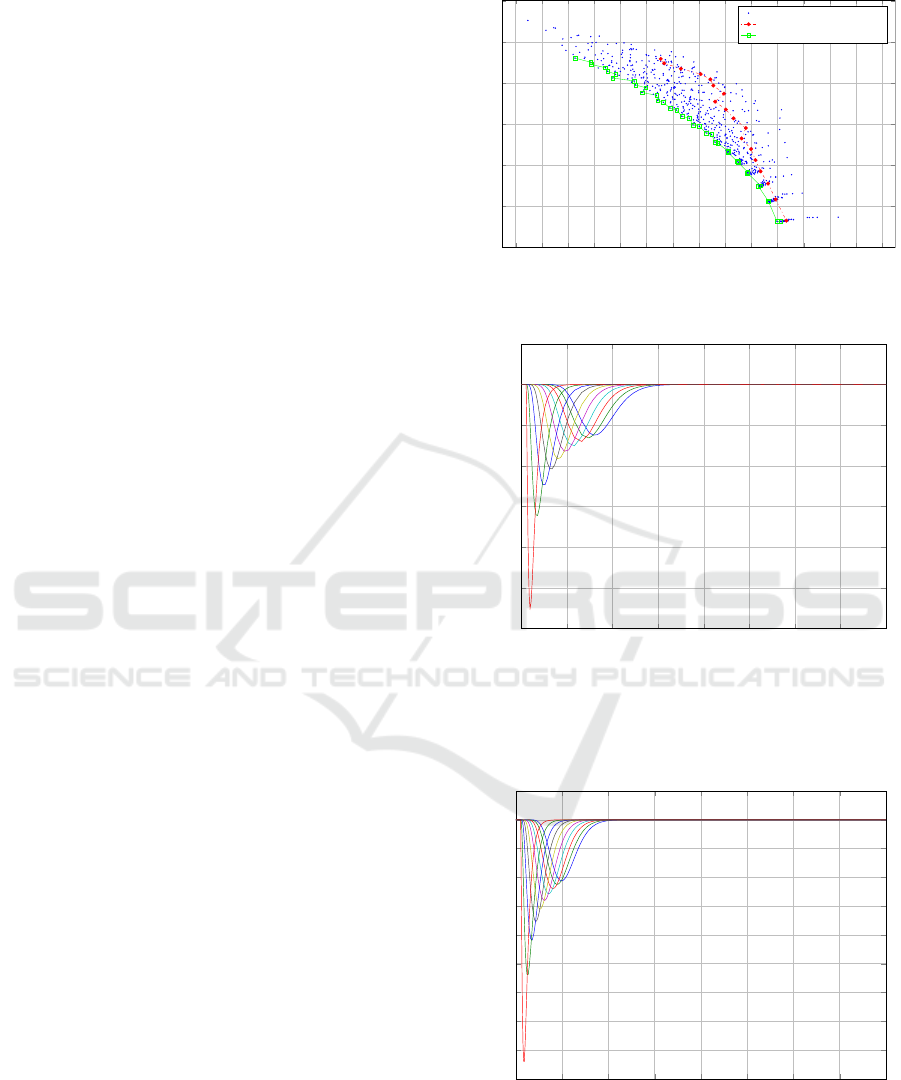
The results of this procedure are shown in Fig. 6.
We can distinguish a number of randomly generated
controllers (blue dots) and the Pareto optimal con-
trollers (green line). These are compared with the
tested NRP controllers (red dots). The performance
in terms of spacing errors of a set of “standard” vehi-
cles and a set of Pareto optimal vehicles is plotted in
Figures 7 and 8, respectively.
These results show that an improvement of about
30% can be obtained using a Pareto optimal controller
with respect to using a “standard” controller, indicat-
ing that the proposed optimization strategy can lead
to high-performance ACC systems.
5 CONCLUSIONS
In this paper, a systematic simulation procedure has
first been developed for comparing different Adap-
tive Cruise Control (ACC) policies. Then, a multi-
objective optimization technique, based on a Pareto
efficiency criterion, has been proposed and tested.
The optimal controller designed by means of this
technique showed better results when compared with
the “standard” ACC policies. Future activities will
focus on extending the numerical simulations consid-
ered in this paper to curve situations where the radar is
unable to sense the vehicle in front for a while, com-
paring the comfort indexes of the policies, and on de-
veloping a user-friendly performance ACC optimiza-
tion toolbox.
0.3 0.3 0.3 0.3 0.3 0.31 0.31 0.31 0.31 0.31 0.32 0.32 0.32 0.32 0.32
0
1
2
3
4
5
6
·10
−2
¯
RMS
u
¯
RMS
y
Randomly generated controllers
Tested NRP controllers
Pareto optimal controllers
Figure 6: Pareto optimization.
0 10 20 30 40 50 60 70 80
−12
−10
−8
−6
−4
−2
0
2
Time
Spacing errors
”Standard Vehicle”
Figure 7: Performance of the NRP controllers (τ =
0.5s, L
des
= 40m, h = 1.3s,k = 4, λ = 0.4). The differ-
ent lines correspond to the spacing errors of each NRP con-
trolled vehicle in the stream.
0 10 20 30 40 50 60 70 80
−9
−8
−7
−6
−5
−4
−3
−2
−1
0
1
Time
Spacing errors
Pareto Optimal Vehicle
Figure 8: Performance of the Pareto optimal controllers
(τ = 0.5s, L
des
= 40m, h = 0.9s, k = 10, λ = 1.6). The dif-
ferent lines correspond to the spacing errors of each Pareto
optimal vehicle in the stream.
VEHITS 2016 - International Conference on Vehicle Technology and Intelligent Transport Systems
18

REFERENCES
B. Howard.(2013). What is Adaptive Cruise Control, and
how does it work? http://www.extremetech.com/
extreme/157172-what-is-adaptive-cruise-control-and-
how-does-it-work.
P. Shakouri, A. Ordys, and M. Askari. (2012.) Adap-
tive Cruise Control with stop & go function using
the State-dependent Nonlinear Predictive control ap-
proach. ISA Transactions 51 Elsevier.
P. Shakouri and A. Ordys. (2014). Nonlinear Model Pre-
dictive Control approach in design of Adaptive Cruise
Control with automated switching to cruise control.
Control Engineering Practice 26, pages 160–177.
L. Xiao and F. Gao. (2010). A Comprehensive Review of
the development of Adaptive Cruise Control Systems.
Vehicle System Dynamics, pages 1167–1192.
R. Rajamani. (2012). Vehicle Dynamics and Control. Me-
chanical Engineering Series Springer 2nd ed.
W. Schakel, B. Arem and B. Netten. (2010). Effects of
Cooperative Adaptive Cruise Control on Traffic Flow
Stability. Proceedings of the 13th IEEE Annual Con-
ference on Intelligent Transportation Systems, pages
759–764.
S. Oncu, N. Wouw and H. Nijmeijer. (2011). Cooperative
Adaptive Cruise Control: Tradeoffs between Control
and Network Specifications. Proceedings of the 14th
International IEEE Conference on Intelligent Trans-
portation Systems, pages 2051–2056.
D. Swaroop. (1995). String Stability of Interconnected
Systems: An Application to Platooning in Automated
Highway Systems. PhD dissertation, Dept. Mechani-
cal Eng., Univ. California Berkeley.
D. Yanakiev and I. Kanellakopoulos. (1995). Variable Time
Headway for String Stability of Automated Heavy-
Duty Vehicles. Proceedings of the 34th IEEE Con-
ference on Decision and Control, pages 4077–4081.
D. Yanakiev and I. Kanellakopoulos. (1995). Variable Lon-
gitudinal Control of Heavy-Duty Vehicles for Auto-
mated Highway Systems. Proceedings of the Ameri-
can Control Conference, pages 3096–3100.
D. Yanakiev and I. Kanellakopoulos. (1998). Nonlinear
Spacing Policies for Automated Heavy-Duty Vehi-
cles. IEEE Transactions on Vehicular Technology vol-
ume 47, pages 1365–1377.
K. Santhanakrishnan and R. Rajamani. (2003). On Spac-
ing Policies for Highway Vehicle Automation. IEEE
Transactions on Intelligent Transportation Systems
Volume 4, pages 198–204.
D. Swaroop, J. Hedrick, C. Chien and P Ioannou. (1994). A
Comparison of Spacing and Headway Control Laws
for Automatically Controlled Vehicles. Vehicle Sys-
tem Dynamics: International Journal of Vehicle Me-
chanics and Mobility, pages 597–625.
L. Chi-Ying and P. Huei. (1999). Optimal Adaptive Cruise
Control with Guaranteed String Stability. Vehicle Sys-
tem Dynamics 31, pages 313–330.
D. Swaroop and R. Hundra. (1998) Intelligent Cruise Con-
trol System Design based on a Traffic Flow Specifi-
cation. Vehicle System Dynamics volume 30, pages
319–344.
J. Zhou and H. Peng. (2004). Range Policy of Adaptive
Cruise Control Vehicles for Improved Flow and String
Stability. Proceedings of the IEEE International Con-
ference on Networking, Sensing and Control, pages
595–600.
J. Zhao, M. Oya and A. Kamel. (2009). A Safety Spacing
Policy and its Impact on Highway Traffic Flow. Intel-
ligent Vehicles Symposium, pages 960–965.
J. Wang and R. Rajamani. (2004). Should Adaptive Cruise-
Control Systems be designed to maintain a Constant
Time Gap between Vehicles? IEEE Transactions on
Vehicular Technology volume 53, pages 1480–1490.
J. Wang and R. Rajamani. (2002). Adaptive Cruise Con-
trol System Design and Its Impact on Highway Traffic
Flow. Proceedings of American Control Conference,
pages 3690–3695.
J. Zhou and H. Peng. (2005). Range Policy of Adaptive
Cruise Control Vehicles for Improved Flow and String
Stability. IEEE Transactions on Intelligent Trans-
portation Systems Volume 6, pages 229–237.
B. Brownstein. (1980). Pareto Optimality, External Benefits
and Public Goods: A Subjectivist Approach. Journal
of Libertarian Studies, pages 93–106.
Evaluation and Optimization of Adaptive Cruise Control Policies Via Numerical Simulations
19