
Automated Segmentation of Tumours in MRI Brain Scans
Ali M. Hasan
1,2
, Farid Meziane
2
and Mohammad Abd Kadhim
1
1
College of Medicine, Al-Nahrain University, Baghdad, Iraq
2
School of Computing, Science and Engineering, University of Salford, Manchester, U.K.
Keywords: Magnetic Resonance Scanning, Bounding 3D Box based Genetic Algorithm, Mid-Sagittal Plane, Principal
Components Analysis.
Abstract: The research reported in this paper concerns the development of a novel automated algorithm to identify and
segment brain tumours in MRI scans. The input is the patient's scan slices and the output is a subset of the
slices that includes the tumour. The proposed method is called Bounding 3D Box Based Genetic Algorithm
(BBBGA) and is based on the use of Genetic Algorithm (GA) to search for the most dissimilar regions
between the left and right hemispheres of the brain. The process involves randomly generating a hundred of
3D boxes with different sizes and locations in the left hemisphere of the brain and compared with the
corresponding 3D boxes in the right hemisphere of the brain through the objective function. These 3D boxes
are moved and updated during the iterations of the GA towards the region of maximum dissimilarity between
the two hemispheres which represent the approximate position of the tumour. The dataset includes 88
pathological patients provided by the MRI Unit of Al-Kadhimiya Teaching Hospital in Iraq. The achieved
accuracy of the BBBGA and 3D segmentation of the tumour were 95% and 90% respectively.
1 INTRODUCTION
Medical image processing expanded dramatically
during the last decade and became a popular research
field that attracted interests from various fields such
as mathematics, computer science, engineering,
biology and medicine with applications in clinical
practice and biomedical imaging to examine and
support diagnoses and therapy in human patients. An
important stage of medical image processing is
segmentation which is seen as a complex and
challenging process, particularly with brain images
due to the nature of the images. Indeed, the brain has
a complicated structure and more accurate
segmentation is essential for detecting tumours,
edema in order to describe therapy (Shen et al., 2005).
The edema associates with intracranial brain tumours
and is the result of leakage of plasma into the
parenchyma through dysfunctional cerebral
capillaries (Kaal and Vecht, 2004).
Many works reported in the literature attempted to
detect and classify brain tumours. Saha et al., (2002),
proposed an automated brain tumour and edema
algorithm to implement fast segmentation of MRI
brain scanning images based on the bounding boxes
method. The Bhattacharya coefficient of grey scale
intensity histograms was used as a score function that
locates bounding boxes around the abnormal area in
the MRI slice. This method was used to search in a
parallel way for the most dissimilar region in an MRI
brain scan between the left and right hemispheres in
an axial view of the MRI (Ray et al., 2008).
Khandani et al. (2009) proposed an automated
algorithm for detecting tumour location in MRI brain
images and identified the tumour boundary by using
an unsupervised learning algorithm called Force
algorithm. A set of prior operations such as skull
removal, non-tumour pixels removal by using
histogram analysis and exponential transformation
was first implemented. The tumour area was then
segmented using histogram thresholding.
Bauer et al., (2011) developed an automated
algorithm to delineate the boundary of the brain
tumour by combining Support Vector Machine
(SVM) classifier and subsequent hierarchical
regularization based on Conditional Random Fields
(CRF). SVM was also used by Mikulka and
Gescheidtov (2013) in a segmentation method to
recognize brain tumour, edema and necrosis in T1 and
T2 MRI weighted images.
Nabizadeh and Kubat (2015) developed a fully
automated algorithm for brain tumours recognition
Hasan, A., Meziane, F. and Kadhim, M.
Automated Segmentation of Tumours in MRI Brain Scans.
DOI: 10.5220/0005625900550062
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 2: BIOIMAGING, pages 55-62
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
55
and segmentation in MRI by using five effective
texture-based statistical feature extraction methods
namely first order statistical features, Grey Level Co-
occurrence Matrix (GLCM), Grey Level Run Length
Matrix (GLRLM), histogram of oriented gradient
HOG and linear binary pattern (LBP).
We addressed the above-mentioned
shortcomings, by developing an algorithm that is:
1. Independent of atlas registration in order to avoid
any inaccurate registration process that affects the
measurement of the tumours’ classification
(Nabizadeh and Kubat, 2015).
2. Fully automated with no human intervention or
initialization.
The rest of this paper is organized as follows. In
Section 2, material and methods are described and the
BBBGA method is explained in details in section 3.
In section 4, tumour segmentation by 3D Active
Contour without Edge method is explained and
experimental results are given in Section 5. The
conclusion is drawn in Section 6.
2 MATERIAL AND METHODS
The main objective of this research is to develop and
evaluate an automated algorithm for identifying the
location of tumours in MRI brain slices as well as
identifying the most important slices of pathological
patient to draw the attention of the clinicians to these
slices. The overall flow chart of the proposed
algorithm is shown in Fig. 1. It starts with the data
collection step from the Iraqi hospital, a set of
algorithms in the pre-processing stage and finally the
segmentation algorithm.
2.1 MRI Acquisition
Data collection is an important steps in this study. T2
and T1 weighted images of 88 pathological patients
were collected from the MRI Unit of Al Kadhimiya
Teaching Hospital in Iraq.
Each patient has 32 slices with a slice resolution
of (432×512 pixels), the inter-slice spacing is 5.5 mm,
and slice thickness is 5 mm. The MRI Unit in the
mentioned hospital has faced many problems in
diagnosing and issuing diagnostic reports for a large
number of inpatients and outpatients. The average
number of patients received daily by this unit is over
110 patients a days for a six working days week. Over
2400 patients are scanned monthly taking most of the
clinicians' time in diagnosing and interpreting MRI
slices. The dataset was collected using a SIEMENS
MAGNETOM Avanto 1.5 Tesla scanner. The
provided dataset consists of tumours with different
sizes, shapes, locations, orientations and types.
Figure 1: The Flow Chart of the proposed algorithm.
2.2 Image Pre-processing
Two preprocessing steps are performed on the MRI
brain scans; image enhancement and MRI intensity
normalization due to the intra-scan and inter-scan
image intensity variations and Mid-Sagittal Plane
detection and correction algorithm (Anju et al., 2013;
Lauwers et al., 2010; Aelterman et al., 2008; Bovik,
2009; Nabizadeh and Kubat, 2015).
2.2.1 Unifying the MRI Slices to 512×512
The provided MRI brain slices with a slice resolution
of (432×512) pixels and the proposed algorithm in
this study is implemented on squared slices of
(512×512) pixels. Therefore, the MRI slices are
resized by adding extra zeros' columns from left and
right till reaching to desired slice resolution.
2.2.2 MRI Image Enhancement
Image enhancement techniques are widely used to
refine medical images and improve the visibility of
the important structures in medical images. As well
as enabling the operators to see the details of the
medical image which may not be immediately
observable in the original medical image (Bankman,
2000; William, 2001). Generally, the spatial domain
techniques are more efficient computationally and
require less processing resources for implementation
(Gonzalez and Woods, 2002; Birry, 2013). The
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
56

Gaussian filter is chosen for noise suppression in this
study due to its performance.
2.2.3 Mid-Sagittal Plane Detection and
Correction
The Mid-Sagittal Plane (MSP) identification is an
important step in brain image analysis as it provides
an initial estimation of the brain’s pathology
assessment and tumour detection (Jayasuriya and
Liew, 2012). The human brain is divided into two
hemispheres that have approximately a bilateral
symmetry around the MSP. This means that most of
the structures in one side of the brain have a
counterpart on the other side with a similar shape and
location. The two hemispheres are separated by the
longitudinal fissure that represents a membrane
between the left and right hemispheres (Ruppert et al.,
2011). The MSP extraction methods can be divided
into two groups (Ruppert et al., 2011; Liu, 2009);
Content-based methods that are based on finding a
plane that maximizes a symmetry measure between
both sides of the brain (Christensen et al., 2006;
Ardekani et al., 1997; Khotanlou et al., 2009; Ruppert
et al., 2011) and shaped-based methods that use the
inter-hemispheric fissure as a simple landmark to
extract and detect the MSP (Bergo et al., 2009; Liu,
2009).
In this study, we choose to determine the
orientation of the patient’s head instead of depending
on measuring the symmetry to identify the brain MSP
as we are using the principal components analysis
(PCA) method to compute the distinctive principle
axes that are orthogonal to each other. Those axes are
used to characterize the patient’s head by representing
the spatial distribution of the mass (Liu, 2009).
The proposed algorithm includes five steps; the
first step separates the brain from the background by
using the histogram thresholding approach because
the background normally has much higher number of
unavailing pixels (Nabizadeh, 2015).
The second step uses holes filling morphological
operator to fill the holes that are defined as a
background region of a binary image and surrounded
by connected borders of foreground (Dougherty,
2009; Bovik, 2009; Soille, 2003; Wilson and Ritter,
2000) as shown in Fig. 2.
The third step determines the orientation of the
patient's head using PCA. The PCA method
essentially attempts to transfer the coordinate of the
original data to a new coordinate system. Such that
the maximum variation in the data comes to lie on the
first coordinate. This is known as the first principal
component. The second maximum variation in the
data lies on the second coordinate and so on (Smith,
2002; Wallisch et al., 2014; Manly, 1988).
Figure 2: An example for MRI brain scanning image
segmentation, A) Original MRI image, B) Segmented MRI
image with threshold equal to 25, C) Dilated MRI image,
and D) Filled holes image.
The new coordinates of the given data are
estimated by calculating the eigenvectors which point
in the direction of the new dataset coordinates. The
desirable coordinate that has the highest eigenvalues,
passes through the maximum variation of data,
representing the orientation of the patient's head
(Wallisch et al., 2014). The angle θ between the X-
axis and X’-axis represents the degree of skewness of
the patient’s head during the MRI test as shown in
Fig. 3 and could be calculated using equation (1):
θ
=tan
V
V
(1)
Where, V
1
and V
2
are the eigenvectors which are
related to the maximum eigenvalues.
Figure 3: Original and new coordinates of brain.
The fourth step is a Geometrical transformation
which is widely used in computer graphic and image
analysis. It is used to rotate and correct the patient's
head by the computedθ.
The fifth step is the positioning of the patient’s
head in the centre of the MRI image because
identifying the brain’s abnormality depends
essentially on measuring the symmetry between the
Automated Segmentation of Tumours in MRI Brain Scans
57

two brain’s hemispheres.
The MRI brain slices of each patient have the
same degree of skewness therefore the MSP detection
and correction algorithm is implemented on a single
slice instead of using all slices to avoid computational
complexity. The preferable slice for implementing the
MSP detection and correction algorithm is the slice
which is located in middle of the slices.
2.2.4 Exponential Transformation of MRI
Brain Slices
Exponential transformation is the process of
compressing the low contrast regions in an MRI brain
image and expanding the high contrast region in a
non-linear way. It is used to increase the intensity
difference between the brain tumour and the
surrounded soft tissue (Khandani et al., 2009). This
will help the GA to converge and move the generated
3D box faster and accurately to the abnormal region
of the brain.
3 BOUNDING 3D BOX BASED
GENETIC ALGORITHM
The novel BBBGA is proposed in this study to
identify the location of the tumours in MRI brain
slices automatically without the need for user
interaction. Where, a hundred of 3D boxes with
different sizes and locations are randomly generated
in the left hemisphere of the brain and these 3D boxes
are compared with the corresponding 3D boxes in the
right hemisphere of the brain through the objective
function. The 3D boxes are optimized and moved
using GAs towards the region that maximized the
objective function value. The objective function value
is high when the 3D boxes stands on the tumour
region and low when the 3D boxes stands on the soft
tissues because the tumour is always brighter than the
soft surrounding tissue of the brain (Khandani et al.,
2009). The output of BBBGA is the slices that contain
the tumour and corresponds to the optimized 3D box
that bounded the tumour over the relevant subset of
slices. The BBBGA method does not need image
registration nor intensity standardization in MRI
slices and is an unsupervised method.
3.1 The Design of the GA
There are several issues involved in designing GAs
such as individual size and population size in addition
to choosing the most appropriate operations such as
selection, crossover and mutation methods.
3.1.1 Individual Construction
As mentioned previously, the provided dataset of
MRI brain scanning slices were unified to (512 × 512)
pixels dimensions and each patient has 32 slices. The
3D boxes that are generated randomly in the left side
of the brain are compared with the corresponding 3D
boxes of the right side by using the fitness function.
The size of the search space will be (512 × 256 × 32)
pixels, and each generated 3D box is defined by six
variables that represent the coordinates of the 3D
boxes in the search space. Fig. 4 shows the original
generated 3D boxes by the GA, such that each
generated 3D box in the right hemisphere has a
corresponding 3D box in the right hemisphere.
Figure 4: Representation of one 3D box in the brain left
hemisphere using (x
1
, x
2
, y
1
, y
2
, z
1
, z
2
) coordinates and
opposite region.
Each individual in the GA population denotes the
binary representation of the coordinates of one 3D
box (x
1
, x
2
, y
1
, y
2
, z
1
, z
2
). Where, x
1
and x
2
represent
the height of the 3D box and are subjected to the
following constraints; 1≤ x
1
<512 and x
1
< x
2
≤512.
While y
1
and y
2
represent the width of the 3D box and
are subjected to the following constraints; 1≤ y
1
<256
and y
1
< y
2
≤256, and z
1
and z
2
represent the depth of
the 3D box and are subjected to the following
constraints; 1≤ z
1
<31 and z
1
< z
2
≤32. Fig. 5 shows
how the coordinates of the 3D box (x
1
, x
2
, y
1
, y
2
, z
1
,
z
2
) are mapped to the individual of the GA in a binary
form where, this individual represents one 3D box
with the coordinates (135, 220, 23, 196, 10, 16).
Figure 5: Individual structure.
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
58

x
1
and x
2
variables are composed of nine bits as
they vary from 1 to 512, while y
1
and y
2
variables are
composed of eight bits and vary from 1 to 256 and z
1
and z
2
variables are compose of five bits and vary
from 1 to 32. Subsequently, the individual size
becomes equal to 44 bits. By using the objective
function, we can measure the performance of
individuals in the problem domain (Chipperfield et
al., 1994). In this study, the fittest individuals that
have the highest numerical value of the associated
objective function are preserved. The objective
function g that is used in this study is based on finding
the absolute value of subtracting the means of the
intensities inside the generated 3D box in the left
hemisphere from the corresponding 3D box in the
right hemisphere using equation (2):
g=
1
x,
y
,z
I
(i,j,k)−I
(i,j,k)
,,
,,
,,
,,
(2)
Where x, y and z are the coordinates of the generated
3D box on the left hemisphere and the corresponding
opposite region in the right hemisphere.
4 TUMOUR SEGMENTATION
USING 3D ACTIVE CONTOUR
WITHOUT THE EDGE
METHOD
The principle goal of the segmentation process is to
partition a medical image into sets of regions. It is an
important step in medical image processing and has
been used in many medical applications (Bankman,
2000). The Active Contour approach, also known as
the Snakes method is the most popular method and
was introduced by Kass et al., (1988). It is a very
successful approach for image segmentation. It
generates a snake or contour within an image domain.
The contour can be moved and directed under the
effect of internal forces within the same contour and
external forces from the image data (Xi-ping et al.,
2002). The location of the contour in the given image
is associated with the energy function E which is,
minimum when the contour reaches the object
boundary within the image. Through an iterative
process the contour deforms and the associated
energy is updated until reaching the minimum value
or the maximum number of iteration is reached. In
this study, we use the 3D active contour without edge
model as proposed by Chan and Vese (2001). This
model can detect object boundaries with or without
gradient, even when the object boundaries are very
smooth or with discontinuity because the main idea
of this method is to consider also the information
inside the object not only at its boundaries (Rousseau,
2009, Klotz, 2013). To fully segment the tumour, the
3D active contour without edge method is applied on
all MRI brain slices of each patient, where the initial
contour is defined as a 3-dimensional 3D box inside
the desired object and optimally selected by the
BBBGA method. The segmentation of all patients
were compared with the reference image (manual
segmentation) which is segmented by experts, such
that the true positive (TP) represents the number of
pixels which are correctly segmented, the false
positive (FP) represents the number of pixels which
are incorrectly segmented, the false negative (FN)
represents the number of pixels which are available in
the reference image and outside the segmented image
by the proposed algorithm, and the true negative (TN)
represents the summation of TP, FP and FN rates
(Anbeek et al., 2005). The accuracy of segmentation
is defined as follows (Nabizadeh and Kubat, 2015):
=
(+)
(+++)
×100
(3)
5 EXPERIMENTAL RESULTS
AND DISCUSSION
To evaluate the proposed algorithms which were
proposed in this study a set of examples will be
implemented using these algorithms.
5.1 MSP Detection and Correction
Results
Fig. 6 shows examples of detecting and correcting the
MSP of the brain of three MRI brain scanning images
which are oriented with different directions. The MRI
brain scanning image is shown in Fig. 7, is re-sampled
using the Geometric Rotator system object in
MATLAB Image Processing Toolkit (Matlab, 2013),
to rotate the patient’s head with different yaw angles
from -10 to 10 degrees in 5 degree intervals. The
proposed algorithm is evaluated by comparing the
achievable results with the proposed algorithms in
(Liu and Collins, 1996) as shown in Table 1. It is
noted that there is a significant difference in the mean
squared error (MSE) between the proposed
algorithms.
Automated Segmentation of Tumours in MRI Brain Scans
59
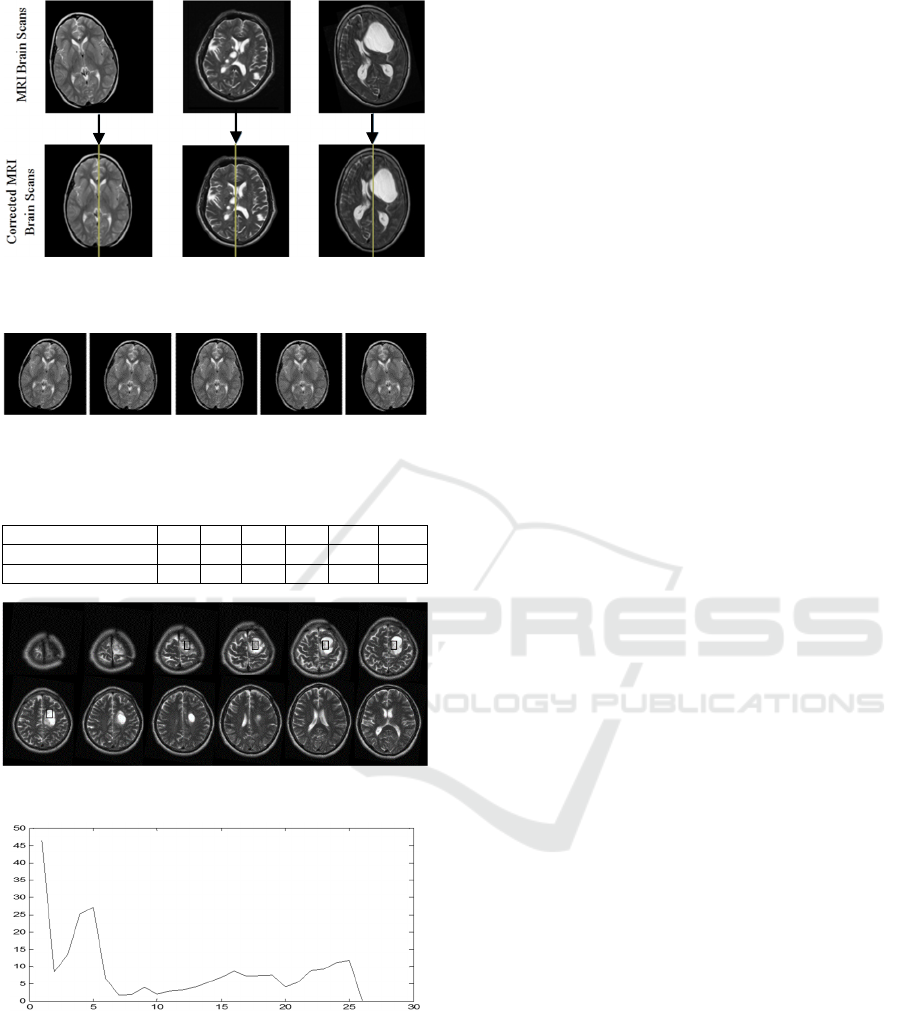
Figure 6: MSP detection and correction of three
pathological patients.
Figure 7: Re-sampling of one slice from the axial MRI brain
scanning image with varied rotate angles.
Table 1:
Numerical results of detecting yaw angle.
Yaw Angle -10 -5 0 5 10 MSE
Computed Yaw Angle -9.1 -4.7 0.5 5.4 10.5 0.3
(Liu and Collins, 1996) -8.5 -3 1.25 6.5 11.2 2.87
Figure 8: MRI brain scanning slices.
Figure 9: RMSE over 27 iterations by GA.
Once the patient's head is corrected, we apply the
BBBGA method to localize the brain tumour. Fig. 8
shows the output of BBBGA implementation on MRI
brain scanning slices of pathological patient with a
population size equal to 100 and a mutation rate equal
to 0.05. The optimal selected slices are 3 to 7. Fig. 9
shows how the RMSE decreases to the minimum
value within 27 iterations of GA. The achievable
accuracy by BBBGA was 95%, such that, there were
only 4 cases where the system has failed to identify
the abnormality because of the tumour's size is less
than 1 cm
3
.
5.2 Tumour Segmentation Results
Fig. 10 shows the result of segmentation of a
pathological patient, who has a brain tumour starting
from slice 2 and ending in slice 9. The MRI scans in
the dataset are manually segmented by expert and the
achievable segmentation accuracy was 90±3.7% by
3D Active Contour without Edge method. The same
dataset was segmented by 2D Active Contour without
Edge method and the achievable accuracy was
86.9±3.7%. Fig. 11 shows a comparison between the
3D and 2D segmentation of given dataset, such that it
is noted that the 3D segmentation outweighs the 2D
segmentation for all patients in the given dataset.
Subsequently, it is possible to identify the most
relevant slices to draw the attention of the clinicians
about these slices instead of spending long time on
diagnosing and interpreting MRI slices. Fig. 12 shows
a comparison of identifying clinically and
experimentally the most relevant slices for the
provided pathological patients after segmentation.
We have test the null hypothesis to prove that there is
no significant difference was found between
automatic and manual identification of slices showing
the tumor (t-test, p=0.86).
6 CONCLUSION
This paper presented an automated system that is able
to detect the location of tumour and then segment it
automatically in addition to identifying the most
relevant slices that should be diagnosed by clinicians
without requiring to inspect all patients’ slices.
The BBBGA method exploits the symmetry
feature of axial viewing of MRI brain slices to search
about the most dissymmetry region in the brain,
additionally it is unsupervised method meanwhile it
does need for training phase and it does not need for
image registration.
A major difficulty of segmentation with a white
matter tumours because of overlapping of the
intensity distributions of the white and grey matter.
As well as, some parts of the tumours in the grey
matter cannot be distinguished due to finite resolution
of the images and complicated shapes of the brain
tissues that impact on a large number of the voxels
which are located on the borders of tissues. In
addition, image intensity in the centre of tumour is
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
60
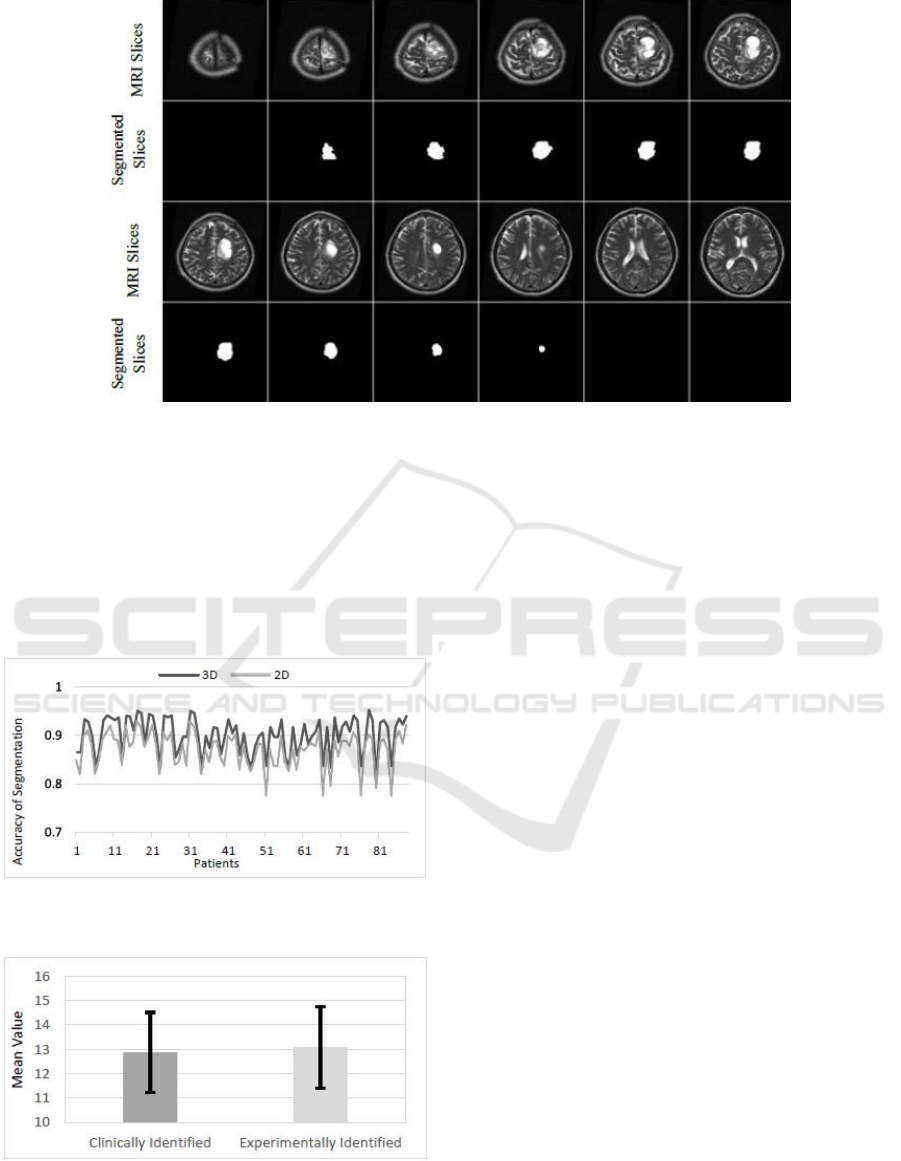
Figure 10: The result of segmentation of T2 weighted MRI brain slices by3D active contour without edge segmentation
method.
different from its Periphery. Therefore, the image
intensity at the borders of tumour may be the same as
grey matter. This phenomenon may cause confusion
between grey matter and tumours and result in
misclassification of the peripheral regions of the
tumours, which is occurred in T2 weighted.
Figure 11: Comparison between 3D and 2D segmentation
for given dataset.
Figure 12: Comparison between clinically and
experimentally MRI slice identification.
ACKNOWLEDGEMENTS
We would like to thank the MRI Unit in Al
Kadhimiya Teaching Hospital in Iraq for providing us
the diagnosed dataset of MRI brain scanning images.
REFERENCES
Aelterman, J., Goossens, B., Pizurica, A. & Philips, W.
2008. Removal of correlated rician noise in magnetic
resonance imaging. 16th European Signal Processing
Conference. Switzerland.
Anbeek, P., Vincken, L., Van Bochove, S., Van Osch, P. &
Van Der Grond, J. 2005. Probabilistic segmentation of
brain tissue in MR imaging. NeuroImage, 27, 795-804.
Anju, E., Karnan, M. & Sivakumar, R. 2013. MR brain
image classification with supervised bacteria foraging
technique using SVM. International Journal of
Futuristic Science Engineering and Technology, 1,
318-322.
Ardekani, A., Kershaw, J., Braun, M. & Kanno, I. 1997.
Automatic detection of the mid-sagittal plane in 3-D
brain images. IEEE Trans Med Imaging, 16, 947-52.
Bankman, I. (ed.) 2000. Handbook of medical imaging:
Academic Press, Inc.
Bauer, S., Nolte, L. & Reyes, M. 2011. Fully Automatic
Segmentation of Brain Tumor Images using Support
Vector Machine Classication in Combination with
hierarchical Conditional Random Field Regularization.
Medical Image Computing and Computer-Assisted
Intervention-Springer Berlin Heidelberg, 354-361.
Bergo, F., Falcão, A., Yasuda, C. & Ruppert, G. 2009. Fast,
Accurate and Precise Mid-Sagittal Plane Location in
Automated Segmentation of Tumours in MRI Brain Scans
61

3D MR Images of the Brain. Biomedical Engineering
Systems and Technologies. Springer Berlin Heidelberg.
Birry, R. 2013. Automated Classification in Digital Images
of Osteogenic differentiated stem Cells. PhD,
University of Salford, Manchester.
Bovik, A. 2009. The Essential Guide to Image Processing,
Elsevier Inc.
Chan, F. & Vese, A. 2001. Active contours without edges.
Image Processing, IEEE Transactions, 10, 266-277.
Chipperfield, A., Fleming, P., Pohlheim, H. & Fonseca, C.
1994. Genetic Algorithm TOOLBOX for Use with
MATLAB.
Christensen, J., Hutchins, G. & Mcdonald, C. 2006.
Computer automated detection of head orientation for
prevention of wrong-side treatment errors. AMIA Annu
Symp Proc, 136-40.
Dougherty, G. 2009. Digital Image Processing for Medical
Applications.
Gonzalez, R. & Woods, R. 2002. Digital Image Processing.
Jayasuriya, S. & Liew, A. 2012. Symmetry plane detection
in neuroimages based on intensity profile analysis.
Information Technology in Medicine and Education
(ITME), International Symposium on. Australia IEEE.
Kaal, E. C. & Vecht, C. J. 2004. The management of brain
edema in brain tumors. Current opinion in oncology,
16, 593-600.
Kass, M., Witkin, A. & Terzopoulos, D. 1988. Snake:
Active Contour Models. International Journal of
Computer Vision, 1, 321-331.
Khandani, M., Bajcsy, R. & Fallah, Y. 2009. Automated
Segmentation of Brain Tumors in MRI Using Force
Data Clustering Algorithm. Advances in Visual
Computing. Springer Berlin Heidelberg.
Khotanlou, H., Colliot, O., Atif, J. & Bloch, I. 2009. 3D
brain tumor segmentation in MRI using fuzzy
classification, symmetry analysis and spatially
constrained deformable models. Fuzzy Sets and
Systems, 160, 1457-1473.
Klotz, A. 2013. 2D and 3D multiphase active contours
without edges based algorithms for simultaneous
segmentation of retinal layers from OCT images. MS.c,
University of Texas at Austin.
Lauwers, L., Barbé, K., Van Moer, W. & Pintelon, R. 2010.
Analyzing Rice distributed functional magnetic
resonance imaging data: a Bayesian approach.
Measurement Science and Technology, 21, 115804.
Liu, S. 2009. Symmetry and asymmetry analysis and its
implications to computer-aided diagnosis: A review of
the literature. Journal of Biomedical Informatics, 42,
1056-1064.
Liu, Y. & Collins, R. 1996. Automatic Extraction of the
Central Symmetry (MidSagittal) Plane from
Neuroradiology Images. Robotics Institute, Carnegie
Mellon University.
Manly, B. 1988. Multivariate Statistical Methods A primer,
Department of mathematics and statistics, university of
Otago.
Matlab 2013. The Math Works kit.
Mikulka, J. & Gescheidtov, E. 2013. An Improved
Segmentation of Brain Tumor, Edema and Necrosis.
Progress In Electromagnetics Research Symposium
Proceedings, Taipei.
Nabizadeh, N. 2015. Automated Brain Lesion Detection
and Segmentation Using Magnetic Resonance Images.
PhD, University of Miami.
Nabizadeh, N. & Kubat, M. 2015. Brain tumors detection
and segmentation in MR images: Gabor wavelet vs.
statistical features. Computers & Electrical
Engineering.
Ray, N., Greiner, R. & Murtha, A. 2008. Using Symmetry
to Detect Abnormalies in Brain MRI. Computer Society
of India Communications, 31, 7-10.
Rousseau, O. 2009. Geometrical Modeling of the Heart.
Ph.D, University of Ottawa.
Ruppert, G., Teverovskiy, L., Chen-Ping, Y., Falcao, X. &
Yanxi, L. A new symmetry-based method for mid-
sagittal plane extraction in neuroimages. Biomedical
Imaging: From Nano to Macro, International
Symposium on, 2011 Chicago, IL. IEEE, 285-288.
Shen, S., Sandham, W., Granat, M. & Sterr, A. 2005. MRI
fuzzy segmentation of brain tissue using neighborhood
attraction with neural-network optimization.
Information Technology in Biomedicine, IEEE
Transactions on, 9, 459-467.
Smith, L. 2002. A tutorial on Principal Components
Analysis.
Soille, P. 2003. Morphological Image Analysis: Principles
and Applications, Springer-Verlag New York, Inc.
Wallisch, P., Lusignan, M., Benayoun, M., Baker, T.,
Dickey, A. & Hatsopoulos, N. 2014. Matlab for
Neuroscientists, Elsevier.
William, K. 2001. Digital Image Processing, Canada,
Wiley-Interscience.
Wilson, J. & Ritter, G. 2000. Handbook of Computer Vision
Algorithms in Image Algebra, CRC Press, Inc.
Xi-Ping, L., Jie, T. & Yao, L. 2002. An Algorithm for
Segmentation of Medical Image Series Based on Active
Contour Model. Journal of Software, 13, 1050-1058.
BIOIMAGING 2016 - 3rd International Conference on Bioimaging
62
