Comparison of GPU-based and CPU-based Algorithms for

Determining the Minimum Distance between a CUSA Scalper and

Blood Vessels

Hiroshi Noborio

, Takahiro Kunii

and Kiminori Mizushino

Department of Computer Science, Osaka Electro-Commun. Univ., Kiyotaki 1130-70, 575-0063, Shijo-Nawate, Osaka, Japan

Kashina System Co. Hirata-Cho 116-22, 522-0041, Hikone, Shiga, Japan

Embedded Wings Co., Ine 5-2-3 562-0015, Minoh, Osaka, Japan

Keywords: Parallel Processing, GPGPU, Z-Buffering, STL, DICOM, CT/MRI, CUSA.

Abstract: In this study, we have designed a GPGPU (General-Purpose Graphics Processing Unit)-based algorithm for

determining the minimum distance from the tip of a CUSA (Cavitron Ultrasonic Surgical Aspirator) scalpel

to the closest point around three types of blood vessel STLs (STereo-Lithographies). The algorithm consists

of the following two functions: First, we use z-buffering (depth buffering) as the classic matured function of

the GPU in order to effectively obtain depths corresponding to image pixels. Second, we use multiple cores

of the GPU for parallel processing so as to calculate the minimum Euclidean distance from the scalpel tip to

the closest z-values of the depths. Therefore, the complexity of the GPU-based algorithm does not depend on

the shape complexity (e.g., patch, edge, and vertex numbers) of the blood vessels.

1 INTRODUCTION

We are currently developing simulators and

navigators for liver surgery. In general, in liver

surgery, the tissue around the affected area (for

example, cancer tissue) is fractured or emulsified

with the CUSA scalpel used for ultrasound surgery

and extracted. Simultaneously, small blood vessels

having a diameter of 0.5 mm or less can be severed

while in hemostasis by cauterizing with an electric

scalpel, but severing larger vessels will cause

significant bleeding and threaten the life of the

patient. To avoid such an issue, it is ideal for the

doctors to perform actual liver surgery as planned

beforehand by regularly confirming the position of

the blood vessels.

In general, DICOM (Digital Imaging and

COmmunication in Medicine) data obtained by CT

(Computed Tomography)/MRI (Magnetic Resonance

Imaging) are used for recording the liver conditions.

In this study, we first classify the cell tissue into the

entire liver, portal veins, arteries, and veins through a

special processing of the DICOM data. This is called

liver segmentation (Zhang, 1994; Foruzan and Chen,

2013). Here, we represent the three types of blood

vessels in an STL-format polyhedron. Further, the

CUSA, which is a device that incises the liver, is

represented in the same STL with a 3D scanner.

This is because a representation in the STL format

accurately maintains the normal vector of the object

surface and the texture and feel of the distance of the

shape can be accurately felt. However, if these are

represented with a polyhedron (such as B-reps), the

basic processing of surgical simulations will be

relatively time consuming, such as the calculation of

the embedded distance between the polyhedra and the

embedded region as well as the calculation of the

shortest distance in all directions including the

operational directions of the polyhedral, as listed in

Table 1.

To begin with, sensory information related to

sight and touch is required for surgery. To obtain such

information, we need to calculate the distance and/or

the intersection between the CUSA and the liver or

the three types of blood vessels. Since the 1980s,

boundary structures (polyhedra such as B-reps [STL

is a type of these structures] and set operations on

primitives such as CSG [Constructive Solid

Geometry]), volume representations such as voxel

arrays and their hierarchical representations (such as

Oct-Tree, OBB [Oriented Bounding Boxes], and

AABB [Axis-Aligned Bounding Box]) have been

128

Noborio, H., Kunii, T. and Mizushino, K.

Comparison of GPU-based and CPU-based Algorithms for Determining the Minimum Distance between a CUSA Scalper and Blood Vessels.

DOI: 10.5220/0005634801280136

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 128-136

ISBN: 978-989-758-170-0

Table 1: Advantages and disadvantages of CPU-based models and GPU-based Z-buffer (BES: best, BET: better, NOR:

normal, WOR: worst, *1: Normal vector, history, and shape convexity cannot be used. *2: Normal vector, history, and shape

convexity can be used).

processed. Simultaneously, their distance has been

extracted by many CPU-based algorithms (Canny,

1986; Gilbert et al., 1988; Quinlan, 1994; Noborio et

al., 1989), and/or their intersection has been

determined by other CPU-based algorithms (Noborio

et al., 1989; Gottschalk et al., 1996; Bergen, 1997).

However, irrespective of the method used, the

computational time is proportional to (in the order of

O(n) and O(log(n)) the degree of complexity of the

shape of the polyhedron representing the organ

operated on (with n being the number of surfaces).

As contrasted with the above CPU-based high-

speed algorithms, GPGPU (General-Purpose GPU)

has been recently used for accelerating algorithms of

computer vision, 3D structure modeling, 3D

simulators, sorting, databases, and so on (Hubert,

2007; Miura et al., 2013; Pelletier, 2008; Cederman,

2008; Green et al., 2012; Yasuda, 2008; Taylor et al.,

2008; Lee et al., 2014; Modat et al., 2010). With

respect to the calculation of the distance and the

intersection between a point and an object or multiple

objects, the GPGPU has two advantages. One is fast

digitalization (to digitalize all the objects) by z-

buffering, which is the classic matured function of a

GPU. The other is the fast parallel calculation (to

calculate the minimum Euclidean distance or volume

intersection between a point and an object and/or

multiple objects) by using multicores of a GPU in

parallel.

When an STL is to be processed by z-buffering, a

z-value is calculated for each pixel that lies within the

boundary of the STL. If the z-value at a pixel indicates

that the STL is closer to the viewer than the z-value in

the z-buffer, the z-value recorded in the buffer is

replaced by the STL’s value (Joy, 1996). Further, the

Z value of the fastest patch can be preserved through

the GPU background removal function. Therefore, a

cuboid can be obtained with the width and pixilation

calculated using the Z value of the surface and the

reverse side of the polyhedron, resulting in a cuboid

digital approximation of the polyhedra.

Furthermore, we calculate Euclidean distances

from the tip of the scalpel to rectangular

parallelpipeds in parallel by using multicores of the

GPU in order to select the minimum value as the

shortest distance. Therefore, the computational time

is basically in inverse proportion to the core count.

Note that the GPU core count is still enormous and

increases rapidly. However, the conversion time will

no longer depend on the number of surfaces of the

polyhedron.

Therefore, the superimposition calculation of the

liver and the three types of blood vessel cuboids and

the CUSA scalpel cuboids can be performed instantly

by the GPU, and this enables a rapid calculation, by

the GPU, of the embedded distance and the embedded

regions. From this embedding, for example, an

artificial sense of touch is constructed with the

Kelvin–Voigt model, and this can be experienced

through a tactile feedback device. Further, the

polyhedra can be rapidly transformed in response to

the embedded region, and the concave region

becomes visible (Noborio et al., 2013; Onishi et al.,

2014; Onishi et al., 2015).

On the basis of the abovementioned pre-

processing, in this study, we calculate the shortest

distance from the CUSA tip to the three types of blood

vessels (portal veins, arteries, and veins). Herein, we

design a GPU-based algorithm and, by using a CPU,

compare it with a CPU-based algorithm that

calculates the shortest distance from the CUSA tip to

the three types of blood vessel STLs.

The rest of this paper is organized as follows:

Section 2 describes the classic CPU-based algorithm

and the proposed GPU-based algorithm for

calculating the shortest distance from the CUSA tip

to the three types of blood vessels. With respect to the

advantages and disadvantages of GPU-based and

Comparison of GPU-based and CPU-based Algorithms for Determining the Minimum Distance between a CUSA Scalper and Blood Vessels

129

CPU-based algorithms, Section 3 investigates the

effects of the required bit count for a parallel

processing approach, not using the increasing trends

of the computational time when the surface count

increases, actual time shifts in certain liver incision

simulations, and distance errors. Finally, Section 4

summarizes this study.

Figure 1: (a) Minimum distance between a point T and a

patch P in CPU, and (b) minimum distance between a point

T and a set of rectangular parallelepipeds of P in GPU.

2 ALGORITHM TO CALCULATE

THE SHORTEST DISTANCE

In this section, we discuss the CPU-based and GPU-

based algorithms to calculate the shortest

(Euclidean) distance from the CUSA tip to the three

types of blood vessel STLs.

2.1 CPU-based Algorithm

First, we have the tip of the scalpel and the three types

of blood vessel (portal veins, arteries, and veins)

STLs. Next, patch Ps are sequentially chosen from the

three types of blood vessels, and the Euclidean

distance to these is calculated. Finally, the minimum

distance to all the patches is selected, and this is

considered to be the shortest distance to the three

types of blood vessel STLs.

In general, the minimum values of the Euclidean

distance of T and P are obtained from any of the

distances of an infinite plane including Tip T and

Patch P, an infinite straight line including side E of P

and the distance of T, as well as the top V of both tips

of side E and the distance of T. Accordingly, if the leg

of a perpendicular line from coordinate T to a plane

including Patch P falls within Patch P, the length of

the perpendicular line is the shortest distance (Figure

1(a)). Otherwise, the distance to the side including the

top is the shortest distance (Figure 1(a)). Therefore,

the algorithm to calculate the shortest distance is as

follows:

[Step1] Calculate the normal vector n (size

normalized at 1) from the three top points of the blood

vessel’s STL triangular surface (Patch) Pi.

[Step2] Calculate the vector v from any top point of

the triangular surface to the scalpel point T.

[Step3] Get the inner product of normal vector n and

vector v to find the size of the perpendicular vector

from scalpel tip T to the plane.

[Step4] Only for the distance found in [Step3], find

the point going (on the infinite plane) in the opposite

direction of the normal vector from the scalpel tip.

[Step5] Since the intersection in [Step4] is the

intersection with the infinite plane crossing the three

top points, use an outer product for deciding whether

this intersection is within (including sides and top

points) the triangular surface Pi.

[Step6] If the perpendicular line intersects with the

infinite plane outside of the triangular surface Pi, it is

not the shortest distance from the scalpel tip to the

triangular surface Pi. Therefore, reject the

perpendicular line distance to the plane and proceed

to [Step7]. Otherwise, keep it as the shortest distance

candidate di and proceed to [Step8].

[Step7] Of the distances from the tip of the scalpel to

the three sides, keep the shortest distance as the

shortest distance candidate di.

[Step8] Select the smallest value from all triangular

surfaces (Patch) Pi (i: from 1 to n, n: total surface

count) as di. This is the shortest distance to the three

types of blood vessel STLs from the CUSA tip T.

Here, the distance calculation of “points and

surfaces,” “points and sides,” and “points and tops”

in the existing algorithm is checked in a likely order

(Lin and Canny, 1991).

2.2 GPU-based Algorithm

First, using the z-buffering (depth buffering), we

obtain a set of rectangular parallelepipeds along the Z

(depth) axis (Figures 1(b) and 2) in a two-dimensional

XY array. This is a useful function of the GPU, and

therefore, we can obtain the set of rectangular

parallelepipeds very rapidly. For the three types of

blood vessel STLs, we obtain three sets of rectangular

parallelepipeds around the tip T. A large rectangular

region where a doctor operates on the liver by using

CUSA can be freely selected in the world coordinate

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

130

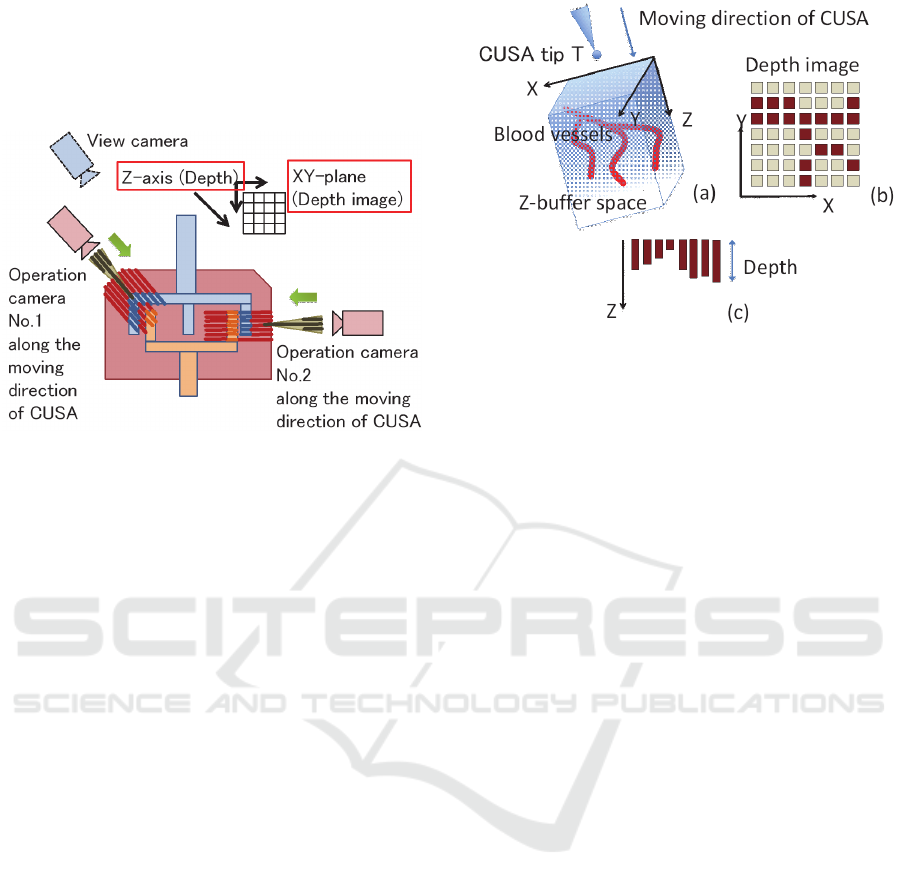
system. In other words, the coordinate system of

depth buffering is defined as a rectangular region,

which implies that rectangular parallelepipeds and the

tip T are transformed into the camera coordinate

system of the depth buffering (Figure 2).

Figure 2: Z-buffer for visible ability and several Z-buffers

for cutting the liver are independently allocated in the world

coordinate (3-D) system.

Next, in the camera coordinate system, we can

calculate the minimum Euclidean distance from the

tip T to the rectangular parallelepipeds in parallel as

the shortest distance by using the many cores of the

GPU (Figure 3). In the assignment to the parallel

processing GPU calculation unit, the thread count is

16 × 16 and the block count is width/16 × height/16.

That is, when the image resolution is 2048 × 2048, a

parallel calculation is performed with a thread count

of 16 × 16 and a block count of 128 × 128.

Finally, in the proposed GPU-based algorithm, we

calculate the distance precision by using two types of

image and depth quantization methods. First, a cuboid

region of X: 106 mm × Y: 106 mm × Z: 213 mm is

established around the scalpel tip to obtain the Z value

of the three types of blood vessel STL surfaces. In

such cases, a 32-bit variable records the Z value, and

the XY image resolution is 2048 × 2048 (Figure 3).

As a result, the quantization error for the Z axis is

about 0.05 nm (=213 mm/2

), and the quantization

error for the XY image is about 52 μm (=106

mm/2048). Therefore, the maximum quantization

error of the Euclidean distance used for calculating

the XYZ value by using the three squares theorem is

73.5 μm. From the perspective of a doctor’s

requirements, this error can be sufficiently ignored.

Moreover, the minimum distance to all pixels is the

shortest distance between the scalpel tip T and the

three types of blood vessel STLs (Figure 3).

Figure 3: Many depths (2 values) in the XY image (many

pixels), which are converted from STL blood vessels.

An array z-buffer[x,y] initialized to ∞

begin /* z-buffering in GPU

for each patch P of three types of vessels do {

for each pixel (x,y) that intersects P do {

calculate z-depth of P at (x,y)

if z-depth < z-buffer[x,y] then {

z-buffer[x,y] = z-depth

}

A vector d-bits[z] initialized to 0

begin /* many cores in GPU

parallel for all pairs of pixels (x,y) and

their z-depth do{

calculate Euclidean distance D between (x,y, z-

buffer[x,y]) and (x

) of tip T of CUSA scalpel

raise a flag at d-bits[z] by D

}

scan d-bits[z] sequentially from left to right in order

to find an initial bit

calculate the distance corresponding to the bit

As shown in Figure 4, even if multiple parallel

processing tasks simultaneously change specific bits,

the existence of their distances is established. In such

cases, if the bit set and the closest XYZ value are

recorded at the same time, multiple proximate vectors

(vectors expressed at the proximity point with the

scalpel tip), which achieve this distance, are

separately recorded. Because all the bits are

initialized, a bit value of 0 implies that a distance

could not be found within the scope corresponding to

any parallel process.

Comparison of GPU-based and CPU-based Algorithms for Determining the Minimum Distance between a CUSA Scalper and Blood Vessels

131

Figure 4: Parallel processing the shortest distance by using

many of the cores in the GPU.

Here, we discuss the relationship between the bit

number and the distance precision in the proposed

algorithm. On the basis of the opinions of doctors, the

ranging scope is set to 0–50 mm, and this is divided

to the extent of 16 × i (variable i is arbitrarily set).

Further, there is a bit for each division, and if there

are any pixels in which the distance from the scalpel

tip to the three types of blood vessels fits within the

bounds of the divisions, this bit is set to 1 (Figure 4).

For example, if i = 1, and the distance error from this

division is 50 mm/16 = about 3 mm, i = 16, then the

distance error from the division is 50 mm/256 = about

0.2 mm. Further, if all arrays are initialized at 0 before

starting the parallel processing for all pixels, when

searching the arrays from 0 after the parallel

processing is finished, in the array in which 1 is first

located, we find the shortest distance by the following

calculation: shortest distance = intermediate value of

the distance range corresponding to the array number

(Figure 4).

Lastly, errors related to this parallel processing are

added to the quantization errors from when the

polyhedra are transformed into Z-buffers. Of course,

in CPU-based algorithms, for parallel processing

errors, there are no quantization errors when the

polyhedra are converted into Z-buffers; there are only

limitations of floating-point numbers (single

precision and double precision). Accordingly,

compared to GPU-based algorithms, there are

relatively few mistakes (Table 2).

Table 2: Comparison of calculation time and distance

precision of CPU- and GPU-based algorithms.

3 EXPERIMENTAL

COMPARISON OF CPU-BASED

ALGORITHMS AND

GPU-BASED ALGORITHM

In this section, we investigate the accuracy of and the

required time for measuring the shortest distance

between the scalpel tip and the three types of blood

vessels. First, we evaluate the computational time for

the two algorithms by monotonically adding the item

count of polyhedral patches that constitute the three

types of blood vessels. Next, we compare the

computational time and the measurement accuracy

when the liver is virtually incised by CUSA.

3.1 PC and Development

Environments

Here, the PC environment and the development

environment related to the CPU and the GPU are

explained in detail.

CPU-related specifications:

(1) PC

 OS Windows 8.1 Professional 64-bit

 CPU Intel Core i5-2500K CPU 3.30 GHz

 Memory 16 GB

(2) Development environment

 IDE Microsoft Visual Studio 2012

 Renderer Direct 3D 11.0

GPU-related specifications:

(1) PC

VGA GeForce GTX480 CUDA processor core count

480

 Graphics clock 700 MHz

 Processor clock 1401 MHz

 Memory 1536 MB GDDR5

(2) Development environment

 Language C++/HLSL

 GPGPU Direct Compute

Since the development environments of CPU-based

and GPU-based algorithms are different, the

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

132

following comparisons may not be precisely fair.

However, our computer has sufficient memory and

the STL’s data size is not very large. Therefore, the

comparisons are practically useful for designing a

surgical simulator/navigator in the future.

3.2 Evaluation of Computational times

of CPU-based and GPU-based

Algorithms

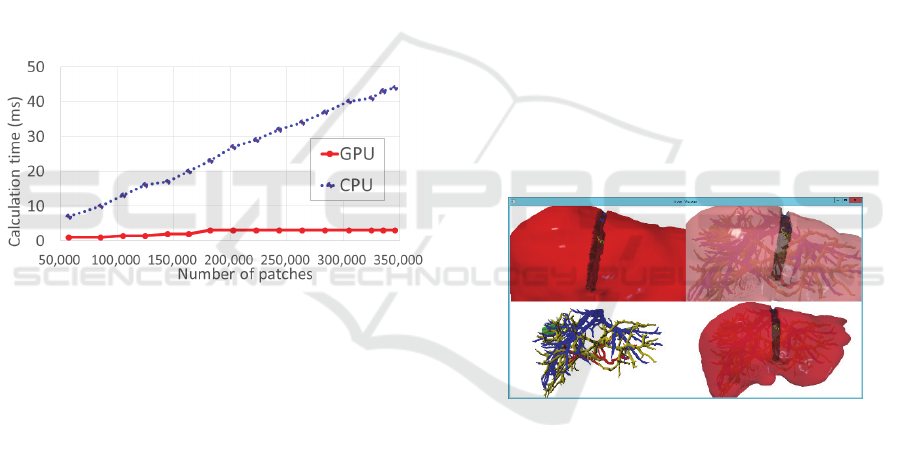
Here, we investigated how the computational time for

each algorithm increases depending on the polyhedra

patch count. First, we place a number of patches for

the three types of blood vessels on the horizontal axis

and monotonically increase the patch count while

increasing the approximate accuracy of the blood

vessel shape to 357992. The computational time for

the CPU- and GPU-based algorithms is shown on the

vertical axis of the graph (unit: milliseconds) (Figure

5).

Figure 5: Computational time of CPU- and GPU-based

algorithms in proportion to the number of patches.

From these results, we found that the computational

time order for algorithms using CPU is O(n) for

surface count n; further, we confirmed that the

computational time increases in proportion to n

(Since this is the shortest distance from the tip of the

scalpel, it is not dependent on the degree of

complexity of the scalpel shape.). This is the same

characteristic as that of conventional algorithms using

CPUs (Lin 1991).

Further, if the accuracy of the polyhedra shape is

increased, the actual computational time will exceed

40 ms. Hence, it will be difficult to obtain not only

the sense of touch but also the reality of sight (The

normal video rate is exceeded.). On the other hand,

the calculation time order of algorithms using the

GPU is O(1), which is a fixed value irrespective of an

increase in n. In the future, since improvement in the

liver segmentation function will allow the recognition

of smaller blood vessels and more accurate shapes,

the polyhedra patch count representing the three types

of blood vessels is expected to increase.

Accordingly, we can state that the computational

time of the GPU-based algorithm, which is

independent of the degree of complexity of the

subject shape, is more desirable than that of the CPU-

based algorithm, which is dependent on the degree of

complexity of the subject shape.

3.3 Changes in Computational Time

for the Shortest Distance between

the Scalpel Tip and the Blood

Vessels in Actual Surgery

Here, we show the computational time required to

derive the shortest distance from the scalpel tip to the

three types of blood vessels when a virtual liver is

actually incised by using a virtual CUSA scalpel.

Figure 6 shows a strobe shot of such an instance, and

Figure 7 shows the time changes exclusively for the

distance calculation of the CPU- and GPU-based

algorithms for each of the motions (the cycle of

moving the scalpel, incising the liver, and measuring

the distance to the three types of blood vessels). Here,

the computational time for the CPU-based algorithm

is more than 40 ms. However, the computational time

for GPU-based algorithms is usually about 3 ms.

Figure 6: Surgery for polyhedral liver and its three types of

blood vessels by using a polyhedron of the CUSA scalpel.

A simulation/navigation of liver surgery needs many

calculation functions such as liver deformation and

real liver sensing and following. The calculation of

the shortest distance is one of them. Therefore, if the

calculation (40 ms) is over the video rate, the surgical

animation of simulation/navigation is sometimes

frozen. Therefore, a faster calculation (2–3 ms) using

a GPU is suitable for real-time simulation/navigation.

A doctor can comfortably follow the instructions for

the surgery when they are provided using smooth

animation. As a result, this real-time animation

reduces the possibility of mistakes made by the

doctor, such as blood vessel injuries in surgery

performed using augmented reality.

Comparison of GPU-based and CPU-based Algorithms for Determining the Minimum Distance between a CUSA Scalper and Blood Vessels

133

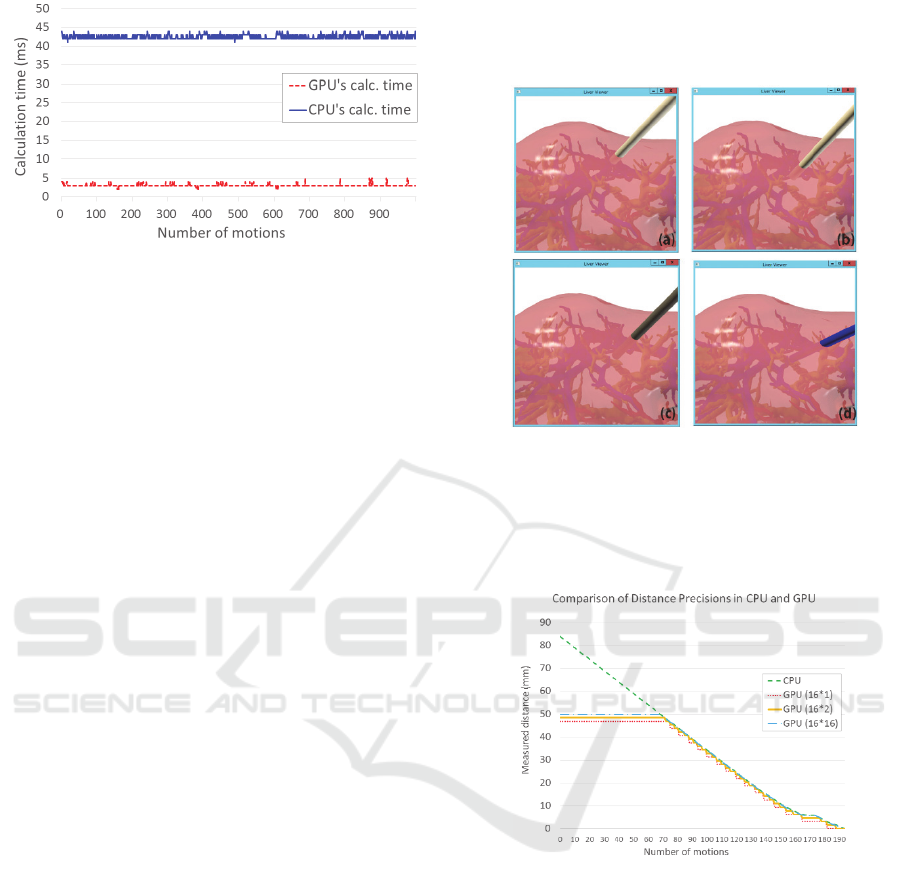
Figure 7: Computational time of CPU- and GPU-based

algorithms in the surgery described in Figure 6.

These results were obtained with the regular-edition

GPU (core count: 480). The current business-use

GPU with thousands of cores will probably be about

five times faster. In contrast, the CPU operating

frequency has hit a plateau since 2007 (around 3

GHz), and Moore’s Law (a three-fold increase in

speed every 2 years) is no longer applicable to the

calculation of computing power. As a

countermeasure, the CPU operating unit counts have

been increased to boost computing power, but the

GPU computing power has improved to a far greater

extent. Therefore, we believe that the GPU-based

algorithm has more of a future than the CPU-based

version.

3.4 Comparison of the Shortest

Distance from the Tip of the Scalpel

to the Three Types of Blood Vessels

Calculated by CPU- and

GPU-based Algorithms in Actual

Surgery

As explained in Section 2 (particularly, the final

paragraph of Section 2.2), GPU-based algorithms

realize parallel processing and maintain its speed. As

a result, certain distance measurement ranges can

only be measured with a certain degree of accuracy

for the distance. On the other hand, in the case of

CPU-based algorithms, no special consideration is

needed for distance measurement ranges or distance

accuracy (naturally, this is still conditioned by the

calculation accuracy of floating-point numbers)

(Table 2).

Here, we actually validated these characteristics.

To begin with, Figure 8 shows the scalpel motion in

a validation experiment, and Figure 9 shows the

trends in distance measurement ranges and distance

accuracy for CPU- and GPU-based algorithms in such

cases. Here, CPU-based algorithms calculated all the

shortest distances without any restrictions, but GPU-

based algorithms calculated the shortest distances for

fixed distance measurement ranges (0–50 mm) with

fixed distance accuracy (50/(16 × i) mm, i: optional).

Figure 8: Motion example in which the CUSA scalpel

accesses three types of blood vessels. In this figure, as long

as the distance decreases monotonously, the color of the

CUSA scalpel changes from white to light gray, dark gray,

and then blue (black). From this color change, a doctor

understands the present state of danger.

Figure 9: Range and precision of distances change when the

CUSA is close to the blood vessels along the sequence of

motions shown in Figure 8.

As compared to the CPU-based algorithm, the GPU-

based algorithm is very fast and its complexity does

not depend on the shape of the blood vessels. On the

other hand, the CPU-based algorithm deals with a

continuous boundary, and therefore, its distance

precision is very good. Unfortunately, the GPU-based

algorithm always digitalizes the shape of blood

vessels by image pixels and their z-buffering.

Consequently, it decreases the distance precision.

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

134

4 CONCLUSIONS

In this paper, we proposed an algorithm to calculate

the shortest distance from the scalpel tip to the blood

vessels independent of the degree of complexity of

the shape of the three types of blood vessels. This

satisfies the specifications required by doctors (with

respect to the distance measurement range, distance

accuracy, and computational time).

To begin with, the opinion among liver surgeons

(as opposed to cerebrovascular and cardiovascular

surgeons) is that a positioning accuracy of about 0.5

cm is sufficient for liver surgery (conversely, human

behavioral functions cannot adjust to any higher

degree of accuracy). It is reportedly the case that the

direction of distance measurement, movement of the

scalpel (incision mistakes only occur in this

direction), and distance measurement range are

acceptable at about 10 cm from the tip of the scalpel

(only around the liver cancer to be cut out; the size of

the entire liver is about 20 cm). Moreover, the

surgeons voiced their desire for a real-time nature

(within a range of several milliseconds in all

situations) that calculates the senses of vision and

touch to be emphasized. The algorithm proposed in

this paper meets this request even when the shapes of

the three types of blood vessels inside the liver are

complex.

Currently, the number of cores in a GPU is

increasing every year. The proposed algorithm can

keep pace with this increase. Further, the technology

for blood vessel imaging and its segmentation is

improving every year, with smaller blood vessels as

well as their more detailed shapes being recognized.

Since this results in an enormous surface count for the

STL expressing the three types of blood vessels, the

value of the GPU-based algorithm proposed here that

calculates the shortest distance to the blood vessels is

expected to increase.

Lastly, an issue to consider in the future is the

development of an algorithm with the guidance

control of the scalpel tip to incise about 0.5 cm around

cancer cells in order to remove them. Toward this

end, it is necessary to enable the calculation of the

shortest distance from all directions of the scalpel tip

and calculate the proximity vector from the scalpel tip

to the closest point on the cancer tissue surface in

order to calculate the operational vector of the scalpel.

Further, we developed a CUSA tip for the cutting

region, but if the kidneys or the other organs, and not

the liver, were the target, then CUSA cannot be used;

blades or scissors would have to be employed to make

the incision. In such cases, we would need to

represent the cutting area with a line and not a point.

In the future, we would like to consider expanding the

proposed algorithm to such instances.

ACKNOWLEDGEMENTS

We would like to express our sincere gratitude to

Professor Masanori Kon and Associate Professor

Masaki Kaibori of Kansai Medical University, who

provided us with advice concerning liver surgery, and

Professor Yen-Wei Chen of Ritsumeikan University,

who provided the segmented liver DICOM data.

Further, we would like to note that this research has

been partially supported by the Collaborative

Research Fund for Graduate Schools (A) of the Osaka

Electro-Communication University and a Grant-in-

Aid for Scientific Research of the Ministry of

Education, Culture, Sports, Science and Technology

(Research Project Number: 26289069).

REFERENCES

Zhang Z. Iterative point matching for registration of free-

form curves. Int. J. Comput. Vision 2, pp.119-152,

1994.

Foruzan A.H., Chen Y.W. et al. Segmentation of liver in

low-contrast images using K-means clustering and

geodesic active contour algorithms. IEICE Trans 4,

pp.798-807, 2013.

Canny J.F. Collision detection for moving polyhedral. IEEE

Trans PAMI 2, pp.200-209, 1986.

Gilbert E., Johnson D., Keerthi S. A fast procedure for

computing the distance between complex objects in

three-dimensional space. IEEE J. Robotic. Autom. 2,

pp.193-203, 1988.

Quinlan S. Efficient distance computation between non-

convex objects. IEEE J. Robotic. Autom.’94, pp.3324-

3329, 1994.

Noborio H., Hata H., Arimoto S. Algorithms searching for

the nearest point of 3-D objects using octotree. IPSJ

Trans 3, pp.311-320, 1989 (in Japanese).

Noborio H., Fukuda S., Arimoto S. Fast interference check

method using octree representation. Adv. Robotics 3,

pp.193-212, 1989.

Gottschalk S., Lin M.C., Manocha D. OBBTree: A

hierarchical structure for rapid interference detection.

SIGGRAPH ‘96, New Orleans, pp.171-180, 1996.

Bergen G. Efficient collision detection of complex

deformable models using AABB trees. Journal of

Graphics Tools 4, pp.1-13, 1997.

Hubert N. GPU Gems 3: Programming Techniques for

High-Performance Graphics and General-Purpose

Computation, Addison-Wesley Professional; First

version, 2007.

Miura M., Fudano K., Ito K., Aoki T., Takizawa H.,

Kobayashi H. Performance evaluation of phase-based

Comparison of GPU-based and CPU-based Algorithms for Determining the Minimum Distance between a CUSA Scalper and Blood Vessels

135

correspondence matching on GPUs. Proc. SPIE 8856,

Applications of Digital Image Processing XXXVI,

885614, 26 September 2013.

Pelletier M. G. Parallel algorithm for GPU processing for

use in high speed machine vision sensing of cotton lint

trash. Sensors 8(2), pp.817-829, 2008.

Cederman D. On sorting and load balancing on GPUs.

ACM SIGARCH Computer Architecture News

Archive 36(5), pp.11-18, December 2008.

Green O., McColl R., Bader D. A. GPU merge path - A

GPU merging algorithm. Proc. of the 26th ACM

International Conference on Supercomputing (ICS),

San Servolo Island, Venice, Italy, June 25-29, pp.

331

–

340,

2012.

Yasuda K. Accelerating density-functional calculations

with graphics processing units. Journal of Chemical

Theory and Computation 4(8), pp.1230-1236, August

2008.

Taylor Z. A, Cheng M., Ourselin S. High-speed nonlinear

finite element analysis for surgical simulation using

graphics processing units. IEEE Trans Med Imaging

27(5), pp.650-663, 2008. doi:

10.1109/TMI.2007.913112.

Lee H.-P., Audette M., Joldes G. R. and Enquobahriea A.

neurosurgery simulation using non-linear finite element

modeling and haptic interaction. Proc. SPIE Int. Soc.

Opt. Eng. Author manuscript; available in PMC 2014

Jan 22. Published in final edited form as: Proc. SPIE Int.

Soc. Opt. Eng. 2012 Feb 23; 8316: 83160H. doi:

10.1117/12.911987.

Modat M., Ridgway G. R., Taylor Z. A., Lehmann M.,

Barnes J., Hawkes D. J., Fox N.C., Ourselina S. Fast

free-form deformation using graphics processing units.

Journal of Computer Methods and Programs in

Biomedicine 98(3), pp.278–284, June 2010.

Joy K. The Depth-Buffer Visible Surface Algorithm, On-

Line Computer Graphics Notes,

http://www.idav.ucdavis.edu/education/GraphicsNotes

/Z-Buffer-Algorithm/Z-Buffer-Algorithm.html, 1996.

Lin M., Canny J. A. Fast algorithm for incremental distance

calculation. IEEE Robotics and Automation ’91,

Sacramento, pp.1008-1014, 1991.

Noborio H, Onishi K, Koeda M, Mizushino K, Kunii T,

Kaibori M, Kwon M, Chen YW. A fast surgical

algorithm operating polyhedrons using Z-buffer in

GPU. Proc. of the 9th Asian Conference on Computer

Aided Surgery, Tokyo, pp.110-111, 2013.

Onishi K., Mizushino K., Noborio H., Koeda M. Haptic AR

dental simulator using Z-buffer for object deformation.

Proc. of the HCI International 2014 (16th International

Conference on Human-Computer Interaction), Creta

Maris, Heraklion, Crete Greece, pp.342-348, June 22-

27, 2014.

Onishi K., Noborio H., Koeda M., Watanabe K., Mizushino

K., Kunii T., Kaibori M., Matsui K., Kwon M. Virtual

liver surgical simulator by using Z-buffer for object

deformation. Universal Access in Human-Computer

Interaction (Proc. of HCII 2015), Part III, LNCS 9177,

pp.345-351, Los Angeles, CA, USA, August 2015.

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

136