
Environmental Data Recovery using Polynomial Regression
for Large-scale Wireless Sensor Networks
Kohei Ohba
1
, Yoshihiro Yoneda
1
, Koji Kurihara
2
, Takashi Suganuma
1
, Hiroyuki Ito
1
,
Noboru Ishihara
1
, Kunihiko Gotoh
1
, Koichiro Yamashita
2
and Kazuya Masu
1
1
ICE Cube Center, Tokyo Institute of Technology, Nagatsutacho 4259, Midori-ku, Kanagawa, 226–8503, Japan
2
Network Systems Laboratory, Fujitsu Laboratories Ltd., Kamikodanaka 4–1–1,
Kawasaki Nakahara-ku, Kanagawa, 211–8588, Japan
Keywords:
Wireless Sensor Networks, Polynomial Regression, Data Recovery, Environment Monitoring.
Abstract:
In the near feature, large-scale wireless sensor networks will play an important role in our lives by monitoring
our environment with large numbers of sensors. However, data loss owing to data collision between the sensor
nodes and electromagnetic noise need to be addressed. As the interval of aggregate data is not fixed, digital
signal processing is not possible and noise degrades the data accuracy. To overcome these problems, we have
researched an environmental data recovery technique using polynomial regression based on the correlations
among environmental data. The reliability of the recovered data is discussed in the time, space and frequency
domains. The relation between the accuracy of the recovered characteristics and the polynomial regression
order is clarified. The effects of noise, data loss and number of sensor nodes are quantified. Clearly, polynomial
regression offers the advantage of low-pass filtering and enhances the signal-to-noise ratio of the environmental
data. Furthermore, the polynomial regression can recover arbitrary environmental characteristics.
1 INTRODUCTION
Large-scale wireless sensor networks (WSNs) use
wireless sensor nodes to monitor environmental pa-
rameters such as temperature, humidity, pH, light
and air pressure. WSNs have many possible appli-
cations, ranging from structual health monitoring to
field monitoring. Thanks to the progress in micro-
electronics based on the integrated circuit technology,
small wireless sensor nodeswith low power consump-
tion have been achieved. However, problems exist
with data loss owing to data collision between the
sensor nodes and electromagnetic noise. As the in-
terval of aggregate data is not fixed in the time and
space domains, digital signal processing using Fourier
or wavelet transforms cannot be applied directly to
the aggregated data. Moreover, noise degrades the
data accuracy. Because the environmental character-
istics have various waveforms, data reliability cannot
evaluate by signal analysis. To overcome these prob-
lems, various techniques, such as data collection tim-
ing (Sivrikaya et al., 2004), redundant system (Ya-
mashita et al., 2014) and data recovery (Doherty et
al., 2000), have been used to increase data reliability.
We apply polynomial regression to environmen-
tal data recovery based on the correlations among
the environmental data. Environmental characteris-
tics are recovered as aggregated data from the sen-
sor nodes using polynomial regression. Thus, data
loss is minimized, and the data can be analysed eas-
ily. Basic sinusoidal environmental variations are as-
sumed to evaluate the data recovery with polynomial
regression. If the sinusoidal characteristics can be
modeled appropriately, arbitrary waveform character-
istics, such as single-shot, periodic and non-periodic
waveforms, can also be modelled. The recovered data
accuracy is evaluated by comparing the recovered and
source characteristics.
We have also proposed a data reliability evalua-
tion flowchart that does not rely on signal analysis
(Yoneda et al., 2014). We also clarify the relation
between the accuracy of the recovered characteristics
and the polynomial regression order, and the effects
of data loss and number of sensor nodes is analysed.
Furthermore, we show that the use of polynomial re-
gression has the advantage of low-pass filtering that
enhances the signal-to-noise ratio (SNR) of the envi-
ronmental characteristics. In addition, we show that
polynomial regression can recover arbitrary environ-
mental characteristics.
In section 2, we introduce the environmental data
recovery technique based on polynomial regression.
Ohba, K., Yoneda, Y., Kurihara, K., Suganuma, T., Ito, H., Ishihara, N., Gotoh, K., Yamashita, K. and Masu, K.
Environmental Data Recovery using Polynomial Regression for Large-scale Wireless Sensor Networks.
DOI: 10.5220/0005636901610168
In Proceedings of the 5th International Confererence on Sensor Networks (SENSORNETS 2016), pages 161-168
ISBN: 978-989-758-169-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
161
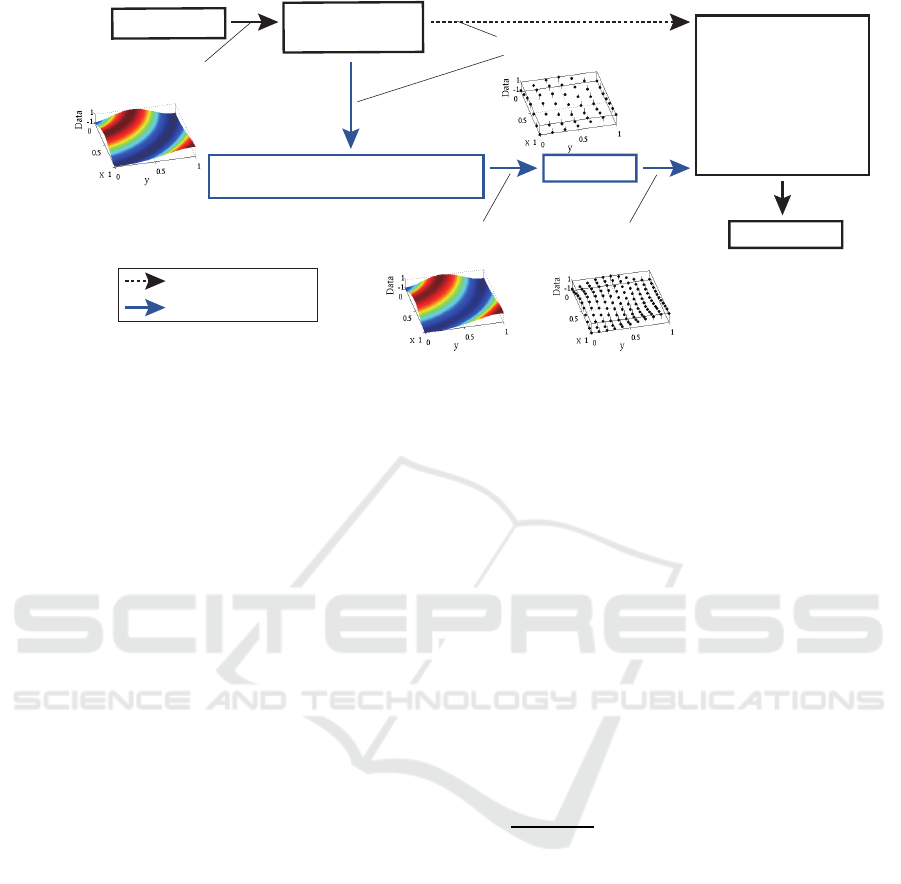
Environment characteristic
(Continuously)
Data aggregation
<WSN>
Recover environment characteristic
by polynomial regression
Recovered function
(Continuously)
Aggregate data
(Discretely)
Conventional approach
Proposed approach
Re-sampling
Recovered data
(Discretely)
-Signal analysis-
Frequency analysis
Fourier transform
Wavelet transform
Time series analysis
etc...
Data utilisation
Environment
Figure 1: WSN system using polynomial regression.
In section 3, the reliability of the recovered data is
discussed. The frequency domain characteristics are
evaluated in section 4. In section 5, we confirm the
ability of polynomial regression to recover arbitrary
environmental characteristics and present the conclu-
sions in section 6.
2 ENVIRONMENTAL DATA
RECOVERY USING
POLYNOMIAL REGRESSION
The aggregated data analysis is shown in Fig. 1. If
the interval of the aggregated sampled data is fixed,
the environmentaldata characteristics can be analysed
directly using Fourier or wavelet transforms. How-
ever, when the interval of the data is not fixed, the
data cannot be directly analysed. Therefore, continu-
ous environmental characteristics are recovered from
the aggregated data, and then, the fixed interval data
are resampled from the recovered characteristics.
2.1 Polynomial Regression
There are several ways of expressing the recovered
characteristics, e.g., Fourier series expansion, polyno-
mial regression, interpolation and so on. Polynomial
regression is simple and suitable for expressing con-
tinuous characteristics as it tolerates data loss. How-
ever, polynomial regression is not good at expressing
characteristics with many inflection points. If the fre-
quency band is limited, the environmental character-
istics at the limited bandwidth can be expressed us-
ing polynomial expressions. Therefore, polynomial
regression is used in environmental data recovery.
When one-dimensional data are t = [
t
1
· ·· t
N
]
T
and the environmental data are d = [
d
1
,· · · ,d
N
]
T
, the
environmental source characteristics function f
W
(t)
can be recovered and recovered function f
R
(t) is
f
R
(t) =
m
∑
i=0
a
i
t
i
(1)
Where a = [
a
0
· · · a
m
]
T
is the coefficient vector.
The value of a is obtained using at least two multipli-
cation methods. m is the order of polynomial equa-
tion. For two-dimensional data obtained by sensor
nodes arranged in coordinates (x
1
,y
1
),· · · , (x
N
,y
N
)
and coordinates x = [
x
1
· · · x
N
]
T
and y =
[
y
1
· · · y
N
]
T
, the recovered function f
R
(x,y) is
f
R
(x,y) =
∑
j, k≥0
j+k≤m
a
jk
x
j
y
k
(2)
Where the coefficient vector a is the column vector of
size
(m+1)(m+2)
2
× 1.
2.2 Data Reliability Evaluation Flow
2.2.1 Evaluation flow
The reliability evaluation flowchart is shown in Fig.
2. Two-dimensional data are assumed in the evalu-
ation. The environmental source characteristic func-
tion is f
W
(x
i
,y
i
). To consider the effect of noise and
data loss, we define the sensor node model. When the
noise is expressed as f
N
(x
i
,y
i
), the sampled data with
noise f
S
(x
i
,y
i
) can be expressed as
f
S
(x
i
,y
i
) = f
W
(x
i
,y
i
) + f
N
(x
i
,y
i
) (3)
To evaluate the effect of data loss, the following func-
tion is added
f
O
(x
i
,y
i
) =
f
S
(x
i
,y
i
) (Without data loss)
/
0 (With data loss)
(4)
SENSORNETS 2016 - 5th International Conference on Sensor Networks
162
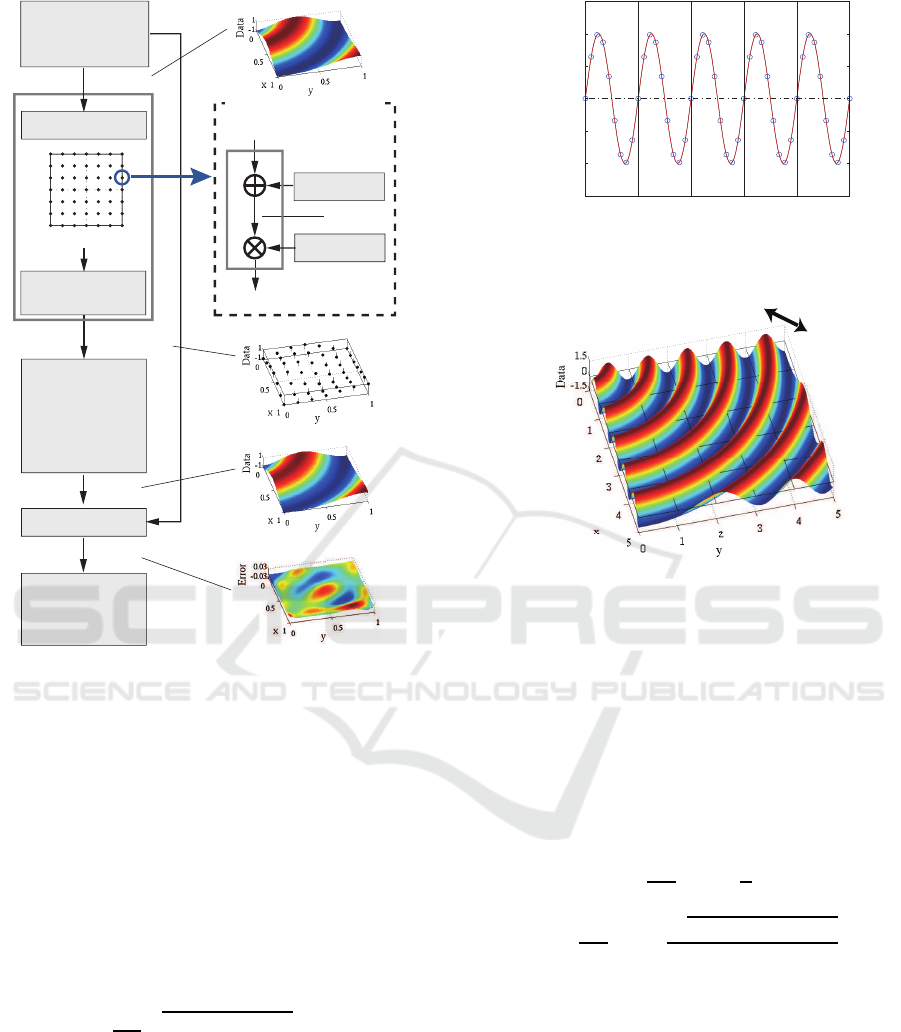
f
W
(x,y)
U
f
O
(x
i
,
y
i
)
f
R
(x,y)
f
E
(x,y)
f
N
(x
i
,
y
i
)
f
W
(x
i
,
y
i
)
f
S
(x
i
,
y
i
)
f
O
(x
i
,
y
i
)
Data loss
0 0.5 1
0
0.5
1
y
x
Generate
environment
characteristics
Sensor node model
Noise
Sensor nodes
Data
aggregation
Recover
environment
characteristics
by polynomial
regression
Extract error
Analyse
data reliability
evaluation
Environment characteristics
Recovered function
Aggregate data
Error data
Figure 2: Data reliability evaluation flow (based on Yoneda
et al., 2014).
Where f
O
(x
i
,y
i
) represents the sampled data consid-
ering the effect of noise and data loss. The amount of
data in f
O
(x
i
,y
i
) decreases compared with the number
of f
S
(x
i
,y
i
). The error of the recovered data is defined
as
f
E
(x,y) = f
R
(x,y) − f
W
(x,y) (5)
The data accuracy that are sampled at fixed intervals
using the above continuous functions are compared
with the accuracy of the evaluated data. The root-
mean-square error (RMSE) at each comparison point
is defined as data reliability. RMSE is given
RMSE =
1
σ
W
q
mean( f
E
(x,y)
2
) × 100(%) (6)
In the evaluation, we carry out 1000 iterations to min-
imize the effect of noise variation and data loss.
2.2.2 Parameter Setting
To evaluate the data recovery reliability, the following
conditions are considered.
0 1 2 3 4 5
−1.5
−1
−0.5
0
0.5
1
1.5
t : Partition region size
Data
(a) one-dimensional case
Partition region size
(b) two-dimensional case
Figure 3: Examples of the recovery function.
Sinusoidal Environmental Characteristics. The
correlations among the actual environmental data are
complex. However, to determine a generalized index,
it is preferable to use simple data characteristics. In
this study, a sinusoidal wave is assumed as the ba-
sic environmental characteristic because any arbitrary
characteristic can be expressed as a linear combina-
tion of a sinusoidal wave. The following equations
are the sinusoidal functions used for one- and two-
dimensional data.
f
W
(t) =
A
pp
2
sin
2π
t
L
+ θ
(7)
f
W
(x,y) =
A
pp
2
sin
2π
p
(x−x
0
)
2
+(y−y
0
)
2
L
+θ
!
(8)
Where (x
0
,y
0
) is showing the position of the wave
generation source, A
pp
is the peak-to-peak amplitude,
L is the wavelength and θ is the phase.
Observation Region. The observation region is the
region where the polynomial regression is applied.
The observation region is partitioned and then
polynomial regression is applied to each partition.
Each data recovery function is joined to express
the characteristics of the observation region. The
partitions of the region are determined by the cycle
Environmental Data Recovery using Polynomial Regression for Large-scale Wireless Sensor Networks
163

0
0.5
0.25
1
1.5
2
2.5
0.5 1 1.5 2
RMSE (%)
Partition region Size
5th order
6th order
7th order
8th order
9th order
(a) one-dimensional case
0
0.5
0.25
1
1.5
2
2.5
0.5
1
1.5
2
RMSE (%)
Partition region Size
5th order
6th order
7th order
8th order
9th order
(b) two-dimensional case
Figure 4: Precision of polynomial regression.
(wavelength) of the highest frequency of the environ-
mental characteristics.
Number of Sensor Nodes. The sensor nodes are
arranged at equal intervals in the observation region,
including the upper boundary. In the case of two-
dimensional structures, the sensor nodes are set on a
grid. The density of the sensor nodes is represented
by the number of sensor nodes N in the observation
region. When the analysis is in the time domain, the
one-dimensional coordinate axis is evaluated with
respect to the time axis. In this case, the number of
sensor nodes in the observation region represents the
number of sampled data.
Noise. Electromagnetic noise generated at the sensor
interface of an amplifier and an analogue-to-digital
converter and electromagnetic noise in the environ-
ment mainly contribute to data noise. The SNR is
defined by following equation.
SNR = 10log
10
var( f
S
)
var( f
N
)
(9)
White noise (Gaussian noise) is added in the reliabil-
ity evaluation.
0.001
0.01
0.1
1
10
1 10 100 1000
RMSE (%)
Number of Sensor Nodes N
order = 9
30 dB
40 dB
50 dB
noise-free
×4
×1/2
(a) 1-dimensional case
0.001
0.01
0.1
1
10
10 100 1000 10000
RMSE(%)
Number of Sensor Nodes N
order = 9
30 dB
40 dB
50 dB
noise-free
×4
×1/2
(b) 2-dimensional case
Figure 5: Required number of sensor nodes.
Data Loss. Data loss occurs because of data colli-
sions or intermittent failures in the wireless commu-
nication. To simulate the effect of data loss, we use a
pseudorandom data generation technique.
3 DATA RELIABILITY OF
PERIODIC CHARACTERISTICS
The reliability of recovered data that are re-sampled
from the recovered function is evaluated by com-
paring with the environmental source characteristics
function. The data reliability is evaluated using the
conditions described in the previous section. Fig-
ure 3 shows the sinusoidal signal that is assumed as
the environmental characteristics of one- and two-
dimensional conditions.
The SNR at each sensor node is set at 40 dB.
Therefore, the reference position of the RMSE is de-
termined at 1.0%. When the number of sensor nodes
is increased, the reference position of the RMSE is
0.5%. Without sensor node noise, the reference posi-
tion of the RMSE is 0.25%.
SENSORNETS 2016 - 5th International Conference on Sensor Networks
164

10
20
30
40
50
60
1 10 100 1000
Precision of Each
Sensor Node (SNR) [dB]
Number of Sensor Nodes N
order = 9
1.0%
0.50%
0.25%
×4
6dB
(a) 1-dimensional case
10
20
30
50
60
10 100 1000 10000
Precision of Each
Sensor Node (SNR) [dB]
Number of Sensor Nodes N
order = 9
1.0%
0.50%
0.25%
×4
6dB
(b) 2-dimensional case
Figure 6: Sensor accuracy (based on Yoneda et al., 2014).
3.1 Application Range of the
Polynomial Regression
Firstly, the relation between the partition region cycle
and RMSE was analysed by changing the order
of the polynomial without the sensor node noise.
The number of sensor nodes is ten for the one-cycle
partition region in the one-dimensional case and 10
× 10 for the one-cycle partition region in the two-
dimensional case. We also examined the five-cycle
partition region and monitored the maximum error.
Results for the one- and two-dimensional sinusoidal
signals (Fig. 3) are shown in Fig. 4. For 0.25% error
and one-cycle partition region, the order of the poly-
nomial should be higher than seven for one- and two-
dimensional signals.
3.2 Effect of Sensor Node Number
The number of sensor nodes is thought to strongly af-
fect the data evaluation reliability. The relation be-
tween the number of sensor nodes and RMSE was
analysed for SNR of 50, 40 and 30 dB at each sen-
sor node. And ninth-order polynomial was used
in the analysis. The results for the one- and two-
dimensional cases are shown in Fig. 5. Obviously,
the errors reduced with the number of sensor nodes.
The increasing number of sensor nodes reduced the
RMSE owing to noise. Figure 6 shows the results
for the required SNR at each sensor node when the
RMSE is 0.25%, 0.5% and 1%. The precision of each
sensor node is improved by increasing the number of
sensor nodes.
There are two ways to improve the data evalua-
tion reliability. The first is to increase the number of
sensor nodes and the second is to use high SNR. If
the number of sensor nodes is increased four times,
the RMSE decreases 50%. If the SNR of each sensor
node is improved by 6 dB, the RMSE decreases by
50%.
3.3 Effect of Data Loss
The relation between data loss rate and the RMSE
was analysed. A ninth-order polynomial and 40-dB
SNR at each sensor node was assumed. The number
of sensor nodes was selected to satisfy the RMSE of
0.5% and 0.25%. In the one-dimensional case, 36 and
149 nodes were selected for the analysis. In the two-
dimensional cases, 225 and 841 were selected.
The results for the one- and two-dimensional
cases are shown in Fig.7. The RMSE increases with
data loss rate, of course. However, by increasing
the number of sensor nodes, the RMSE decreases.
The number of sensor nodes satisfies the RMSE of
0.25% adequately, whereas the data loss rate is 60%
for RMSE of 0.5% in the one-dimensional case and
65% in the two-dimensional case. These results sug-
gest that a redundant system can enhance the data re-
liability.
4 RELIABILITY IN THE
FREQUENCY DOMAIN
The reliability of the recovered data using polynomial
regression was also evaluated in the frequency do-
main (Ohba et al., 2015). The fast Fourier transform
(FFT) was applied to the recovered data.
4.1 FFT Analysis
The one-dimensional sinusoidal environmental char-
acteristics are assumed to be the same as in the pre-
vious sections. Recovered data at fixed intervals are
obtained by sampling the data recovered by polyno-
mial regression. FFT is applied to the recovered data.
The signal-to-noise and distortion ratio (SNDR) and
spurious-free dynamic range (SFDR) were evaluated.
Environmental Data Recovery using Polynomial Regression for Large-scale Wireless Sensor Networks
165

0.1
1
10
0 20 40 60 80 100
RMSE (%)
Data Loss Rate (%)
N = 36
N = 149
0.5
60%
0.25
(a) 1-dimensional case
0.1
0.5
1
10
0 20 40 60 80 100
RMSE (%)
Data Loss Rate (%)
N = 15x15
N = 29x29
65%
0.25
(b) 2-dimensional case
Figure 7: Data loss robustness (based on Yoneda et al.,
2014).
The SFDR is used to discuss the effect of harmonic
distortion.
When the fundamental frequency is f
0
, the num-
ber of FFT points is FFT
POINT
and the sampling fre-
quency is F
S
, f
0
is
f
0
=
F
S
FFT
POINT
(10)
Therefore, the input signal frequency f
in
and wave-
length of the input signal per division λ
in
is
f
in
= m f
0
(11)
λ
in
=
m
D
n
(12)
Where D
n
is the number of divisions and m is an inte-
ger number.
4.2 Data Reliability in the FFT Analysis
4.2.1 Effect of Input Signal Cycle (Wavelength)
The relation between signal cycle (wavelength) in the
polynomial regression and the evaluation indices of
gain, SNDR and SFDR was analysed using FFT. In
the analysis, a ninth-order polynomial, 40-dB SNR at
each sensor node, 32 divisions dividing FFT points
into partition region and 1024 of FFT points are as-
sumed. The results are shown in Fig. 8. This is
showing the relation between input frequency cycle
(wavelength) for polynomial regression and the eval-
uation indexes. Decreases of 1 dB are tolerated by the
SNDR and SFDR and for wavelength with the max-
imum partition of 1.6 cycles. Above 1.6 cycles, the
partition region signals are filtered out. The gain is
flat up to the three-cycle partition region. Thus, the
polynomial regression acts as a low-pass filter. This
means that the SNDR and SFDR improvebecause the
polynomial regression limits the bandwidth of the en-
vironmental signals.
4.2.2 Effect of the Number of Sensor Node
The number of sensor nodes per partition region is
evaluated. The results are shown in Fig. 9. The FFT
results for the source environmental signals were 40-
dB SNDR and 59-dB SFDR. For 13 sensor nodes, the
SNDR is the same as the result of the source envi-
ronmental signals. For 25 sensor nodes, the SNDR is
the same as the result of source environmentalsignals.
Higher SNDR and SFDR are possible by increasing
the number of sensor nodes. By increasing the num-
ber of sensor nodes four times, both SNDR and SFDR
improved by 6 dB.
4.2.3 Frequency Spectrum
The frequency spectrum is evaluated by FFT. The re-
sults are shown in Fig. 10. Based on the results of
Figs. 8 and 9, the 1.6-cycle (wavelength) input sig-
nal region and 25 sensor nodes per partition region
were assumed. Compared with the spectrum of the
source environmental signal, the noise level of the
high-frequency region is filtered out. Table 1 sum-
marizes the FFT results and Table 2 summarizes the
conditions of the FFT analysis. By limiting the ob-
servation region in the polynomial regression, both
SNDR and SFDR are improved.
Table 1: FFT analysis result.
SNDR[dB] SFDR[dBc]
(A) FFT 40.0 59.0
(B) FFT
using recovered data
45.2 59.9
(=B-A) Difference +5.2 +0.9
SENSORNETS 2016 - 5th International Conference on Sensor Networks
166

-12
-9
-6
-3
0
3
0
20
40
60
80
100
0 1 2 3 4
SNDR [dB] SFDR [dBc]
Gain [dB]
Gain [dB]
3
1.6
SNDR [dB]
SFDR [dBc]
λin
Figure 8: SNDR, SFDR and gain vs. input wavelength
(based on Ohba et al., 2015).
30
40
50
60
70
80
10 100 1000
SNDR [dB]
SFDR [dBc]
6dB
×4
25
SNDR = 40.0 [dB]
SFDR = 59.0 [dBc]
×4
SNDR [dB] SFDR [dBc]
Number of Sensor Nodes
N
13
6dB
Figure 9: SNDR and SFDR vs. number of sensor
nodes(based on K. Ohba, 2015).
-100
-80
-60
-40
-20
0
1 10
100
1000
λin = 31/32 (A)
λ
λ
in = 31/32 (B)
using recovered data
m (=fin/f0)
Power spectrum [dB]
in = 3λ
in = 1
λ
Figure 10: Frequency spectrum with and without recovered
data.
Table 2: FFT analysis conditions.
Parameters Conditions
Noise 40[dB]
Polynomial regression order 9
FFT points 1024
Division 32
5 ARBITRARY
CHARACTERISTICS
RECOVERY BY POLYNOMIAL
REGRESSION
In sections 3 and 4, it was clarified that polynomial
regression can recover the sinusoidal environmental
characteristics. Polynomial regression for arbitrary
characteristics is also validated by selecting the or-
der of the polynomial equation for each partition re-
gion. Scale-space filtering (SSF) (Witkin, 1984) and
Akaikefs information criterion (AIC) (Akaike, 1974)
were used to select the partition region and the order
of the polynomial regression based on aggregate data.
The SSF detects extreme values by the convolution
of the Gaussian function. The partition region is ob-
tained as the region between the extreme points. The
AIC is a statistical measure that estimate the quality
of the environmental source characteristics from ag-
gregate data, including noise and data loss. The order
of the polynomial regression for the partition region is
obtained by the SSF. By detecting the extreme values
by SSF and estimating the quality of source charac-
teristics using polynomial regression between the ap-
propriately selected extreme points by AIC, arbitrary
characteristics can be recovered (Haze, et al., 2012).
Figure 11 shows extreme values of arbitrary envi-
ronmental characteristics with 40-dB SNR detected
by SSF. The observation region is divided into par-
tition regions using the extreme values and the order
of polynomial regression is thus optimized. The re-
gions divided by the criterion of extreme values are
the partition regions, and the order of the polynomial
regression is set at each partition region. Figure 12
shows the recovered data from arbitrary characteris-
tics with 40-dB SNR using the SSF, AIC and poly-
nomial regression. The RMSE is under 0.1%; thus,
the polynomial regression can obviously recover the
arbitrary environmental characteristics.
0 0.5 1 1.5 2 2.5 3 3.5 4
−0.5
0
0.5
1
1.5
2
2.5
t
Data
0
0.5
1
Criterion of Extreme value
Environment characteristics: f
O
Extreme value
Figure 11: Extreme values of arbitrary characteristics.
Environmental Data Recovery using Polynomial Regression for Large-scale Wireless Sensor Networks
167
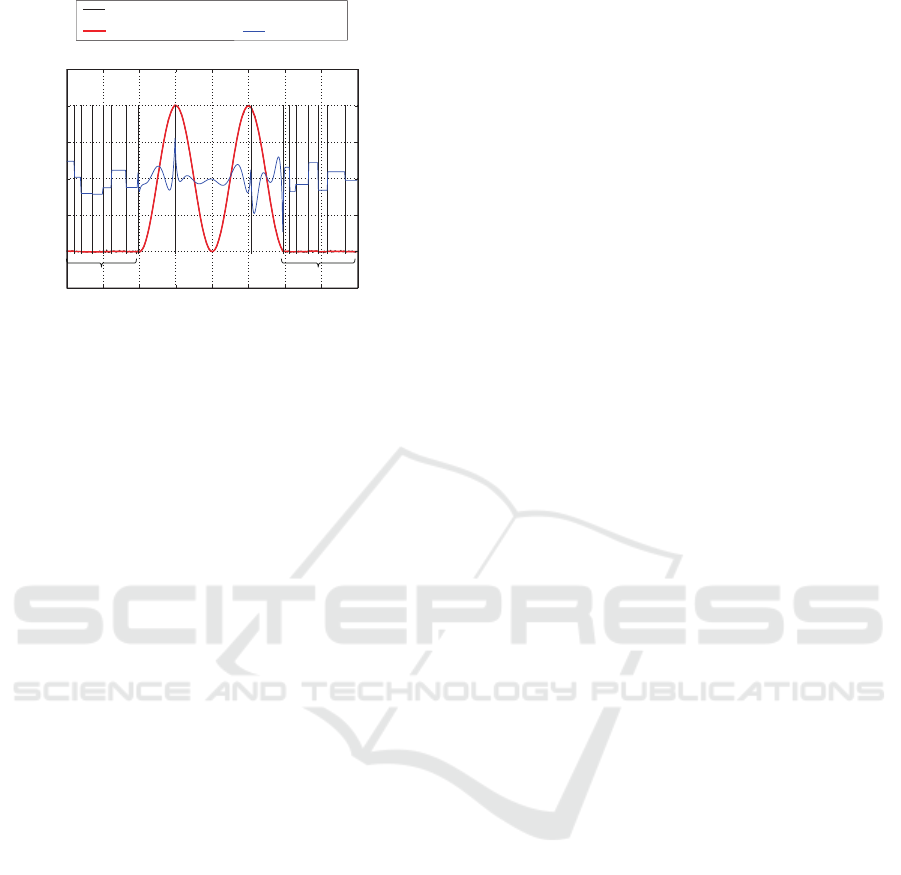
0 0.5 1 1.5 2 2.5 3 3.5 4
−0.5
0
0.5
1
1.5
2
2.5
t
Data
RMSE = 0.0029538 (0.41747%)
6
th
0
th
0
th
5
th
5
th
−0.03
−0.02
−0.01
0
0.01
0.02
0.03
Error
Environment characteristics: f
O
Recovered function: f
R
Error data: f
E
Figure 12: Data recovery function based on arbitrary char-
acteristic.
6 CONCLUSIONS
We used polynomial regression for environmental
data recovery from large-scale WSNs.
(1) A data reliability evaluation procedure for WSN
was proposed.
(2) The recovered data reliability depends on the or-
der of the polynomial regression, the number of sen-
sor nodes and the effect of noise and data loss were
quantified.
(3) From FFT analysis, it is seen that polynomial re-
gression act as a low-pass filter. Data recovery using
polynomial regression enhances the SNDR or SFDR
in the WSNs system.
(4) Polynomial regression can recover arbitrary envi-
ronmental characteristics and can be used with SSF
and AIC.
In conclusion, environmental data recovery tech-
nique using polynomial regression can be applied to
large-scale wireless sensor networks.
ACKNOWLEDGEMENTS
Part of this work was a joint research project of Tokyo
Institute of Technology and Fujitsu Laboratories Lim-
ited. We would like to express our thanks to all who
supported this project.
REFERENCES
Sivrikaya, F., et al., 2004. Time synchronization in sensor
networks: a survey.h Network, IEEE, 18.4: 45-50.
K. Yamashita, et al., 2014. Implementation and Evalua-
tion of Architecture Search Simulator Including Dis-
turbance for Wide-range Grid Wireless Sensor Net-
work.h Multimedia, Distributed, Cooperative, and
Mobile Symposium. 1368-1377.
Doherty, L., et al., 2000. Algorithms for position and data
recovery in wireless sensor networks.h Diss. Depart-
ment of Electrical Engineering and Computer Sci-
ences, University of California at Berkeley.
Y. Yoneda, et al., 2014. A study on Data Reliability Evalu-
ation Index of Wireless Sensor Network for Environ-
mental Monitoring.h The 41st SICE Symposium on
Intelligent Systems.
K. Ohba, et al., 2015. A method of recovering environ-
ment data using polynomial regression for large-scale
wireless sensor networks.h IEICE Technical Report
ASN2015-72.
A. P. Witkin, 1984. SCALE-SPACE FILTERING: A
New Approach To Multi-Scale Description,h IEEE
International Conference on Acoustics, Speech
and Signal Processing, Vol. 9, pp. 150–153,
DOI:10.1109/ICASSP.1984.1172729.
H. Akaike, 1974. A New Look at the Statistical Model Iden-
tification,h IEEE Transactions on Automatic Control,
Vol. AC-19, No. 6, DOI:10.1109/TAC.1974.1100705.
K. Haze, et al., 2012. Modeling home appliance power con-
sumption by interval-based switching Kalman filters.h
Technical Report of IEICE, 112.31: 39-44.
SENSORNETS 2016 - 5th International Conference on Sensor Networks
168
