
Estimation of Working Memory Load using EEG Connectivity
Measures
Sylvie Charbonnier
1
, Raphaelle Roy
1
, Radka Doležalová
1
, Aurélie Campagne
2
and Stéphane Bonnet
3
1
Gipsa-Lab, Univ. Grenoble Alpes, CNRS, Grenoble Campus BP46, St Martin d’Hères, France
2
LPNC, Univ. Grenoble Alpes, CNRS, Grenoble Campus BP46, St Martin d’Hères, France
3
CEA, LETI, Univ. Grenoble Alpes, MINATEC Campus, Grenoble, France
Keywords: Workload, EEG, Connectivity.
Abstract: Working memory load can be estimated using features extracted from the electroencephalogram (EEG).
Connectivity measures, that evaluate the interaction between signals, can be used to extract such features
and therefore provide information about the interconnection of brain areas and electrode sites. To our
knowledge, there is no literature regarding a direct comparison of the relevance of several connectivity
measures for working memory load estimation. This study intends to overcome this lack of literature by
proposing a direct comparison of four connectivity measures on data extracted from a working memory load
experiment performed by 20 participants. These features are extracted using pattern-based or vector-based
methods, and classified using an FLDA classifier and a 10-fold cross-validation procedure. The relevance of
the connectivity measures was assessed by statistically comparing the obtained classification accuracy.
Additional investigations were performed regarding the best set of electrodes and the best frequency band.
The main results are that covariance seems to be the best connectivity measure to estimate working memory
load from EEG signals, even more so with signals filtered in the beta band. point.
1 INTRODUCTION
Monitoring mental states using physiological
signals, and more specifically EEG (electro-
encephalogram) signals, has received more and more
attention from researchers these last years. Indeed, it
possesses numerous human factors applications,
ranging from safety (e.g. driving, nuclear plant
monitoring), to smart technology development
(Fairclough, 2009; Parasuraman et al., 2012).
Several mental states are currently under research
focus, such as mental fatigue, attention, and
affective states. Amongst them is working memory
load, which reflects task difficulty and the associated
mental effort (Gevins and Smith, 2007). This
difficulty can be characterized in terms of quantity
of engaged cognitive resources. Monitoring working
memory load is particularly relevant for
implementing user adaptive interfaces and user
monitoring devices for safe transportation.
Working memory load modulates the EEG
signals recorded on the scalp. Several studies
showed that the band power in the theta (4-8 Hz)
and delta (2-4 Hz) frequency bands at frontal sites
increases with workload, while the band power in
the alpha band (8-12 Hz) at parietal sites decreases
(Holm et al. 2009; Antonenko et al., 2010; Roy et al,
2013).
Working memory load estimation can be
performed thanks to tools that have been developed
for active Brain Computer Interfaces (BCIs). Thus,
most of the processing chains dedicated to workload
estimation that are reported in the literature include a
feature extraction step (e.g. frequency filtering) and
a translation step (e.g. classification). Additionally,
spatial filtering techniques commonly used for
active BCI applications have recently been applied
to enhance working memory load estimation. The
most commonly used features are power band values
or their log variance after spatial filtering (Roy et al.,
2013). Connectivity measures have also, yet less
often, been applied to workload estimation, such as
coherence, phase coherence and functional
connectivity estimated by directed transform
function (resp. Belyavin et al., 2007; Grimes et al.,
2008; Zhang et al., 2015). These measures estimate
interactions between brain regions from EEG
signals. To our knowledge, there is no literature
122
Charbonnier, S., Roy, R., Doležalová, R., Campagne, A. and Bonnet, S.
Estimation of Working Memory Load using EEG Connectivity Measures.
DOI: 10.5220/0005638201220128
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 122-128
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
regarding a direct comparison of the relevance of
several connectivity measures for working memory
load estimation, nor any assessment of the relevance
of pattern-based versus vector-based methods.
The main goal of this article is therefore to
propose a comparison of several connectivity
measures to determine which one enables the more
accurate estimate of working memory load. This
study proposes a traditional signal processing chain
using EEG signals recorded at different locations on
the scalp. It is formed of a pre-processing step, a
feature extraction step, and a classification step
using FLDA (Fisher Linear Discriminant Analysis).
The originality of the method comes from the
features that are used, i.e. connectivity measures,
which are either vector-based or pattern-based
features. Several methods such as cross-correlation,
spatial covariance, spectral coherence and phase
locking value are implemented. Their performance,
measured by the classification accuracy reached, is
compared. The accuracy is computed from a
database extracted from an experiment in which
workload was manipulated by varying the number of
items in working memory load. Additional
investigations were performed regarding the best set
of electrodes and the best frequency band.
The paper is organized as follows. The
experimental design and the data used to evaluate
the performance of the method are described in
section 2, the processing chain and the connectivity
measures are presented in section 3, the results are
detailed and discussed in section 4.
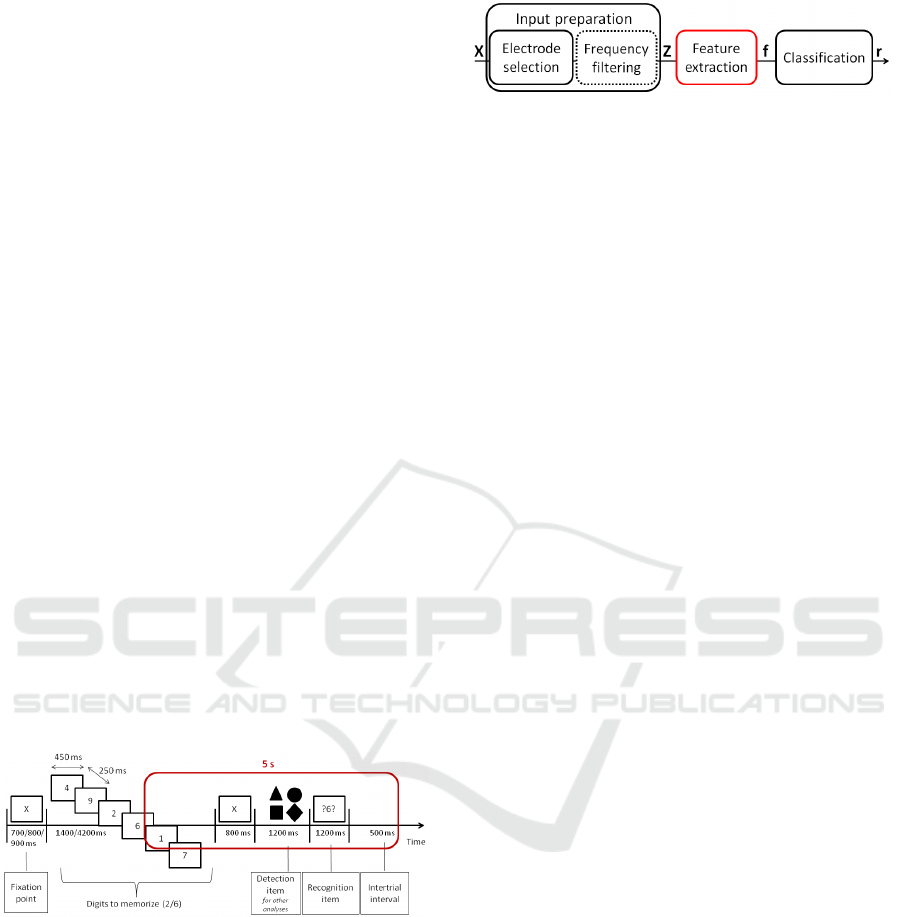
Figure 1: Trial structure. Participants memorize a list of 2
or 6 digits, and answer whether the probe item was in the
list. The circled window was used for analysis.
2 MATERIALS
This research was promoted by Grenoble’s hospital
(France) and was approved by the French ethics
committee (ID number: 2012-A00826-37).
2.1 Experimental Design
Twenty healthy right-handed volunteers (9 females;
Figure 2: Global structure of the processing chain.
age: M = 25 years, S.D. = 3.5) participated in the
experiment. The experiment lasted for 10 minutes
and consisted of 80 trials. For each trial, the
participants had to memorize a list of sequential
digits visually presented on a computer screen.
Then, a probe item flanked with question marks was
displayed (Fig. 1). They had to answer as quickly
and as accurately as possible whether the probe was
present or not in the memorized list using a response
box. Two levels of workload (WKL) were
considered, i.e. 2 and 6 digits to memorize (low and
high WKL respectively). Trials of low and high
WKL were pseudo-randomly presented.
2.2 Data Acquisition and Preprocessing
Participants’ EEG activity was recorded using a
BrainAmpTM system (Brain Products, Inc.) and an
Acticap® equipped with 32 Ag-AgCl active
electrodes that were positioned according to the
extended 10-20 system. The reference and ground
electrodes used for acquisition were those of the
Acticap, i.e. FCz and AFz respectively. The data
were sampled at 500 Hz. The EOG activity was also
recorded using two electrodes positioned at the eyes
outer canthi, and two respectively above and below
the left eye. Moreover, the EEG signal was band-
pass filtered between 1 and 40 Hz, re-referenced to a
common average reference and corrected for ocular
artifacts using the signal recorded from the EOG
electrodes and the SOBI algorithm. Time segments
of 5 s were then selected (circled on Figure 1). Thus,
for each participant, the database consisted of 80 5 s
epochs, 40 in the low WKL condition, and 40 in the
high WKL condition.
3 METHODS
3.1 Processing Chain
Let X be the 5 s epoch. It is a 32 by 2500 matrix.
The processing chain is a traditional one, formed of
a pre-processing step, a feature extraction step and a
classification step (Figure 2).
In the pre-processing step, specific EEG
channels are selected and filtered in a frequency
Estimation of Working Memory Load using EEG Connectivity Measures
123
band of interest using a 5th order Butterworth filter.
The bands are either the theta (4-8 Hz), alpha (8-12
Hz), beta (13-30 Hz) or gamma band (>30 Hz). In
this step, X is transformed into a l by 2500 matrix Y,
with l the number of selected channels. Then, in the
feature extraction step, the feature vector f is
computed from Y using connectivity measures, as
detailed in section 3.2. The length of f depends on
the used connectivity measure. Next, f is
transformed into one of two WKL levels, low or
high, in the classification step.
3.2 EEG Channel Selection
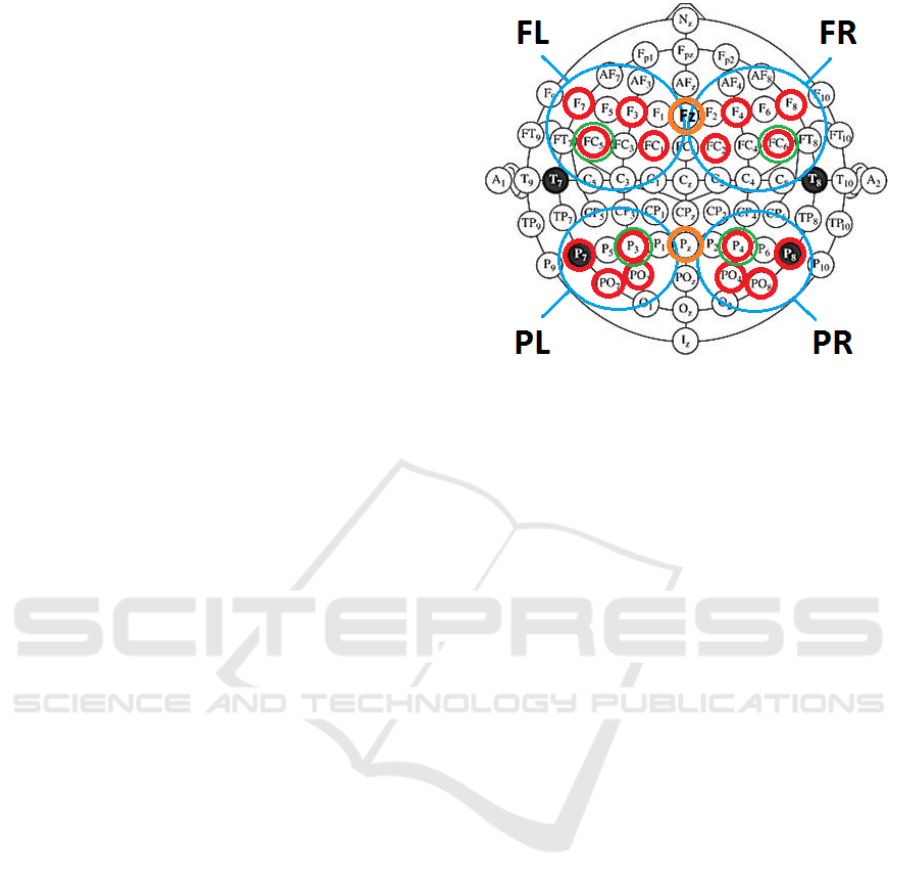
Five different sets of electrodes were used. The
selected channels and thus the brain regions used to
measure interactions between the EEG signals were
different for each set. They were selected according
to the literature as detailed below.
Set 1: In order to analyze the interactions
between frontal and parietal sites, 4 regions of
interest (ROIs) are created: frontal right area (F4,
F8, FC2, FC6), frontal left area (F7, F3, FC5, FC1),
parietal right area (P4, P8, PO4, PO8) and parietal
left area (P3, P7, PO3, PO7). These 4 regions were
reported as regions where EEG is altered when
workload changes (Roy et al, 2013). The EEG
signals of each ROI are averaged to form 4 virtual
electrodes, circled in blue in Figure 3. Here, l is
equal to 4.
Set 2: Only 1 channel is selected from each ROI,
namely FC5, FC6, P3 and P4, circled in green in
Figure 3. This selection is performed so as to check
that no relevant information is lost by merging the
signals into ROIs. Here, l is equal to 4.
Set 3: In order to analyze the interactions
between central and parietal sites in the middle of
the scalp, 2 major electrode sites are selected,
namely Fz, and Pz (Gevins and Smith, 2007), circled
in orange in Figure 3. Here, l is equal to 2.
Set 4: Since connectivity measures of frontal
areas were reported to be particularly sensitive to
workload modulations (Zhang and Tian, 2015), in
order to analyze the interactions between the signals
from only this particular site, 4 electrodes located at
the frontal right site are selected, namely F4, F8,
FC2 and FC6, circled in red in Figure 3. Here, l is
equal to 4.
Set 5: In the same manner, in order to analyze
the interactions between the signals from only this
particular site, 4 electrodes located at the frontal left
site are selected, namely F7, F3, FC5 and FC1,
circled in red in Figure 3. Here, l is equal to 4.
Figure 3: Illustration of the 5 different electrode sets.
3.3 Classification
For each participant, a training set is used to learn
the classification function and a validation set is
used to evaluate the performances. Two different
classification method types are investigated –
pattern-based methods and vector-based methods.
Pattern-based methods are used when the
connectivity measure represents a function in time,
such as cross-correlation or PLV. A pattern of high
WKL (respect. low) is computed by averaging all
the functions extracted from the epochs of the
learning set labelled high WKL (respect. low). The
Euclidian distances between the function extracted
from the candidate epoch of the validation set and
the two patterns are computed and the candidate
epoch is assigned to the label whose pattern is the
closest.
As for vector-based methods, a feature vector is
built from the connectivity measures by selecting
specific values in the measures, such as the mean or
maximal values. The classification method used is
the Fisher’s Linear Discriminant Analysis (FLDA),
which is very popular in BCI (Lotte et al., 2007).
3.4 Performance Evaluation
The performance of each processing chain is
assessed based on its intra-subject binary
classification accuracy with a ten-fold random cross
validation procedure. The 80 epochs of each
participant are randomly split into 10 subsets, which
are used one after the other as a validation set while
the 9 others are grouped to form the training set
while the 9 others are grouped to form the training
set. The performance of the different processing
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
124

chains is compared using statistical tests. Hence,
repeated-measures ANOVAs were used to detect
significant differences amongst group means and
Tukey post-hoc tests were used to find means that
were significantly different from each other. The
first ANOVA had 2 factors –electrode set and
pattern-based classification method (respectively 5
and 2 levels). The second one also had 2 factors –
electrode set and vector-based classification method
(respectively 5 and 7 levels). A single ANOVA
could not be performed to directly compare those
methods as the same number of levels could not be
reached for both. Lastly, an additional ANOVA was
performed for the two best classification methods of
each type and their best electrode set as previously
determined. These had only one factor, namely the
frequency band (5 levels). The significance level
used was α = 0.05.
3.5 Connectivity Measures
Interactions between brain regions were estimated
with 4 connectivity measures: cross-correlation,
covariance, coherence and PLV (for a review on
connectivity measures see Greenblatt et al., 2012).
Cross-correlation, covariance and coherence were
computed using the signals filtered in the [1-40 Hz]
band as well as in the theta (4-8 Hz), alpha (8-12
Hz), beta (13-30 Hz) or gamma band (>30 Hz). PLV
was computed using the signals filtered in the [1-40
Hz] band only.
Let us note l, the number of EEG signals and N
the number of samples in an epoch Y,
y
i,
the signal
n°i and
y
ik
the value at time k of signal n°i.
3.5.1 Cross-correlation
The cross-correlation is a measure of similarity of
two time series as a function of the lag of one
relative to the other. It varies between -1 (negative
linear relationship) to 1 (positive relationship). 0
means that there is no linear relationship. It is
computed as follows:
c
1
Nτ
y
y
σ
y
y
σ
(1)
where and σ
y
denote mean and variance. The
cross-correlation is a function of length 2N-1.
l(l-1)/2 combinations of signals, and thus l(l-1)/2
cross-correlation functions, can be computed from
Y. For the pattern-based methods, the features used
are the l(l-1)/2 functions formed of 2N-1 samples.
Whereas for the vector-based methods, the feature
vector is built by extracting the mean, maximal or
minimal value of each of the l(l-1)/2 functions. Its
length is thus l(l-1)/2.
3.5.2 Covariance
The spatial covariance between y
i,
and y
j,
is
calculated as follows:
1
(2)
The covariance is the non-normalized correlation
at τ=0.
l(l+1)/2 spatial covariances can be calculated
from Y and stored in the feature vector f.
3.5.3 Spectral Coherence
The spectral coherence, also called magnitude
squared coherence, is a measure of the degree of
relationship, as a function of frequency, between two
signals. It is a real-valued function varying between 0
and 1. It is expressed as:
(3)
with f, the frequency in Hz, S
yiyi
, the spectral density
of
y
i
and S
yiyj
the cross power spectral density of y
i
and
y
j
. In this work, the spectral density is computed
using Welch's averaged modified periodogram with a
Hamming window of 512 samples and 50% overlap.
l(l-1)/2 coherence functions can be computed
from Y. For the vector-based methods, the feature
vector is built by extracting the mean or maximal
value of each of the l(l-1)/2 functions.
3.5.4 PLV
The phase locking value (PLV) measures the
stability of the phase difference between two signals
y
i
and y
j
. It is expressed as:
1
(4)
(5)
where M denotes the number of samples in the time
window, φ
1
and φ
2
are instantaneous phases from
analytic signals z
i
, z
j
(5), which can be obtained with
Hilbert transform HT from y
i
, y
j
.
Estimation of Working Memory Load using EEG Connectivity Measures
125
The PLV has values between 0 and 1, where 0
means total randomness and no phase
synchronization between the signals and 1 means
complete phase synchronization. It was computed on
a sliding window of 512 samples with a 75%
overlap, which provided 15 values per epoch. And
l(l-1)/2 PLV functions were obtained per epoch.
For the pattern-based method, the features used
are the l(l-1)/2 functions formed of the 15 samples.
Whereas for the vector-based method, the feature
vector is built by extracting the mean or the maximal
value of each of the l(l-1)/2 functions.
4 RESULTS
Two different types of classification methods were
investigated - pattern based methods (using cross-
correlation or PLV functions) and vector based
methods (using the maximal cross-correlation
amplitude, the covariance, the coherence mean or
maximal value, the PLV mean or maximum value).
The classification accuracy for each participant
(using a ten-fold cross validation method) was
computed for each classification method, each
connectivity measure, each frequency band and each
electrode subset. As detailed earlier, the results were
analyzed using ANOVAs and Tukey’s tests.
4.1 Electrode Sets
The first 2 ANOVAs showed that there was no
statistical difference in the results when different
electrode subsets were used, regardless of the
classification method (pattern-based methods:
p=0.36; vector-based methods: p=0.84).
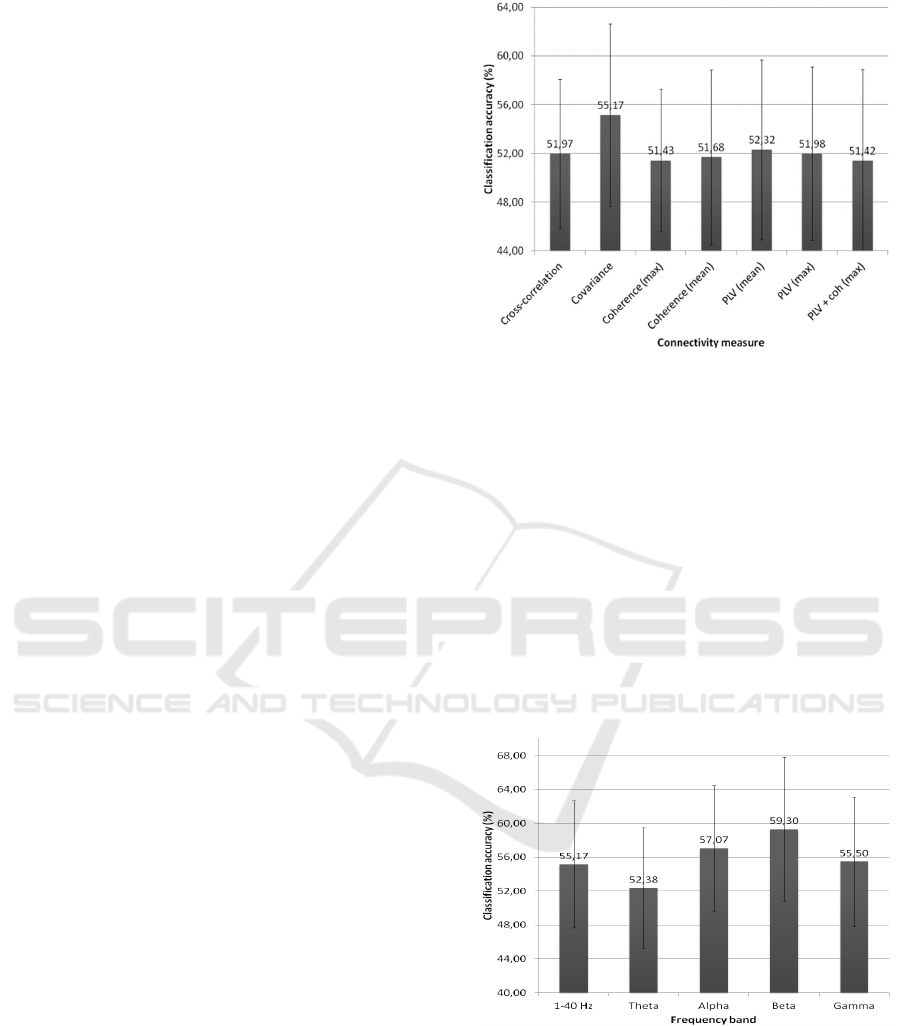
4.2 Classification Methods
When using the pattern-based classification
methods, the cross-correlation function gave better
results than the PLV function regardless of the
electrode set (p<0.05). When using the vector-based
classification methods, the best method was
covariance (p<0.001). It gave the best results
regardless of the electrode set. The classification
accuracies for the vector-based methods are
displayed in Figure 4.
4.3 Frequency Bands
We investigated the chain performance deeper by
assessing the impact of the considered frequency
band. As regards the pattern-based methods,
Figure 4: Mean classification accuracy reached using
signals filtered in the [1-40 Hz] band for each vector-
based method.
cross-correlation gave better results when the signals
were filtered in the [1-40 Hz] band than when the
signals were filtered in the theta or gamma bands
(p<0.05). However, the results were not
significantly different when the signals were filtered
in the alpha or beta band. Regarding the vector-
based classification methods, the best results were
obtained with covariance using the signals filtered in
the beta band (p<0.001). Covariance gave results
that were significantly better in the beta band than in
the [1-40 Hz], theta or gamma bands (p<0.001)
(Figure 5).
Figure 5: Mean classification accuracy obtained using
covariance for each frequency band. 1: [1-40 Hz]; 2: theta;
3: alpha; 4: beta; 5: gamma band.
4.4 Best Results
Amongst all investigated methods, electrode sets and
frequency bands, the best results were obtained with
the covariance when the signals were filtered in the
beta band. The highest mean accuracy, computed
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
126
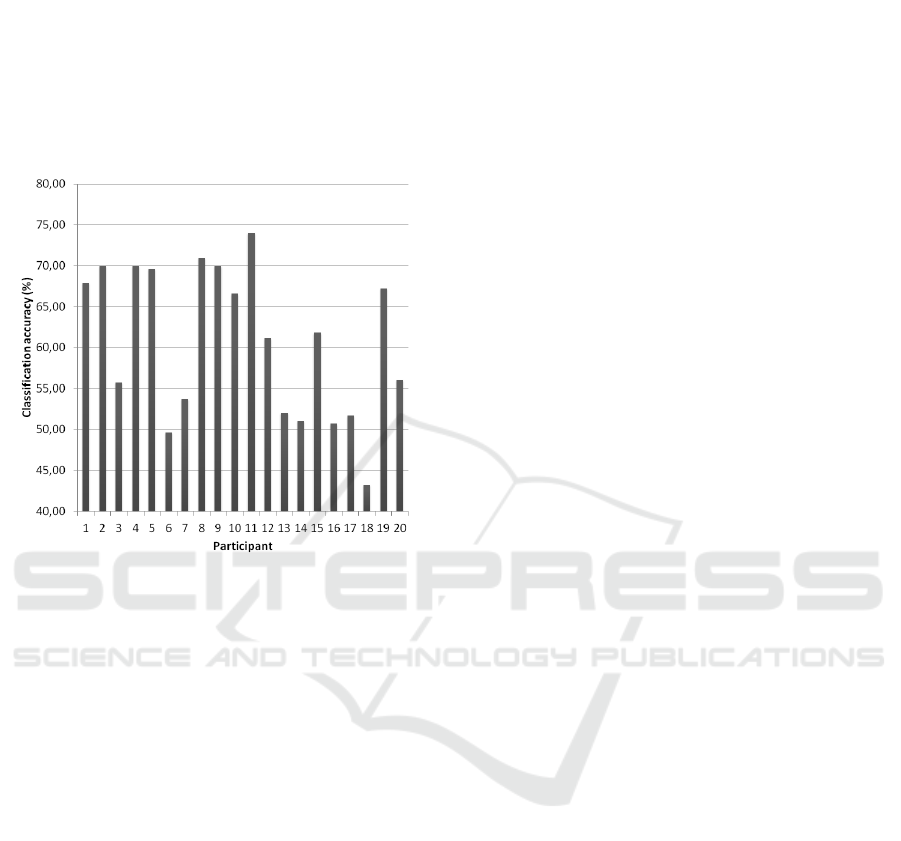
with the 20 participants was 60.64%. It was reached
with the electrode subset #2, with 4 channels
selected from frontal right, frontal left, parietal right
and parietal left areas. It was proved to be
significantly different from random. Figure 6
presents the obtained accuracy in this configuration
for each participant. It can be seen that the
performance reaches at least 70% for 5 participants
out of 20.
Figure 6: Obtained accuracy with the chain based on
covariance in the beta band with the electrode set #2 for
each participant.
The highest accuracy reached with pattern-based
cross-correlation was 57% and was proved to be
significantly different from random. This accuracy
was obtained in the [1-40 Hz] band using electrodes
from the frontal right scalp region (electrode subset
#4).
5 DISCUSSION
This article presents a direct comparison of several
connectivity measures in order to better estimate
working memory load. The best results are reached
using covariance in the beta band with as high as
61% using 4 electrodes evenly distributed on the
scalp.
The global accuracy may seem rather low. Yet,
they are in the same range than the accuracy reached
by Roy and collaborators (2013) on the same data
set, who obtained 63% of mean accuracy. The
processing chain designed by Roy et al. made use of
the 32 electrodes. It consisted of a Common Spatial
Pattern filter able to enhance the signal differences
in the two classes and an FLDA classifier. The best
results were also obtained when the signals were
filtered in the beta band. Therefore here using
covariance, we can reach the same performance
using only 4 electrodes which is a nice improvement
for future real-life implementations. Moreover,
contrary to most of the literature, here we estimate
workload between two states of engagement in a
task. Indeed, several authors obtain very high
classification accuracies, however they only estimate
workload between a state of engagement and a state
of relaxation (e.g. Heger et la., 2010). It should be
better to say that they evaluate task engagement.
Thus, the results have better be compared to that of
Grimes and collaborators (2008) who obtained 65%
of correct classifications. Hence, the results of this
study are in line with the literature and provide
information as to which combination of method,
band and electrode set are the more relevant for
workload estimation.
Regarding the comparison between connectivity
measures, the covariance performed significantly
better than all the other methods. One explanation
could be that the energy of the filtered signals is kept
when the covariance is used while the cross-
correlation, the coherence and the PLV are
normalized values where the information on the
energy of the signal is lost. Energy could be a
discrimant feature to detect workload levels.
Finally, no significant difference could be found
when the different electrodes subsets were used.
This could be explained by the fact that the
electrodes subsets were selected according to the
literature and defined areas that are all known to be
affected by a change in the workload level.
This work shoul be pursued by evaluating the
relevance of covariance for other mental states such
as loss of control for driving applications.
6 CONCLUSIONS
This article presents a direct comparison of several
bivariate connectivity measures in order to better
assess working memory load. Covariance in the beta
band seems to enable a better classification of this
mental state. Only multivariate connectivity
measures were tested. Multivariate measures could
also be tried in the future. This is a promising
preliminary work towards better user state
estimation.
Estimation of Working Memory Load using EEG Connectivity Measures
127

ACKNOWLEDGEMENTS
Grenoble Neurophysiology facility IRMaGe was
partly funded by the French program
“Investissement d’Avenir” run by the “Agence
Nationale pour la Recherche”: Grant
“Infrastructure d’Avenir en Biologie Santé ”
(ANR-11-INBS-0006).
REFERENCES
Antonenko, P., Paas, F., Grabner, R., Gog, T., 2010. Using
electroencephalography to measure cognitive load.
Educational Psychology Review, 22, 425-438.
Belyavin, A., Ryder, C., Dickson, B., 2007. Development
of gauges for the QinetiQ cognition monitor.
Foundations of Augmented Cognition, 3-12.
Fairclough, S. H., 2008. Fundamentals of physiological
computing. Interacting with Computers, 21, 133-145.
Gevins, A., Smith, M. E., 2007. Electroencephalography
(EEG) in Neuroergnomics. In Neuroergonomics: The
brain at work , Parasuraman, R. and Rizzo, M. (Eds),
New York, NY: Oxford University Press Inc.
Greenblatt, R, Pflieger, M. P., Ossadtchi, A., 2012.
Connectivity measures applied to human brain
electrophysiological data. J. Neurosci. Meth., 207 (1),
1-16.
Grimes, D., Tan, D. S., Hudson, S. E., Shenoy, P., Rao, R.
P., 2008. Feasibility and pragmatics of classifying
working memory load with an electroencephalograph,
835-844, ACM Press.
Heger, D., Putze, F., Schultz, T., 2010.Online workload
recognition from EEG data during cognitive tests and
human-machine interaction. Advances in Artificial
Intelligence, 410-417.
Holm, A., Lukander, K., Korpela, J., Sallinen, M., Müller,
K. M. I., 2009. Estimating Brain Load from the EEG.
ScientificWorld J., 9, 639-651.
Lotte, F., Congedo, M, Lécuyer, A., Lamarche, F., B.
Arnaldi, 2007. A review of classification algorithms
for EEG-based brain-computer interfaces. J. Neur.
Eng., 4, R1-R13.
Parasuraman, R., Christensen, J., Grafton, S., 2012.
Neuroergonomics: The brain in action and at work.
NeuroImage, 59, 1- 3.
Roy, R. N., Bonnet, S., Charbonnier, S., Campagne, A.,
2013. Mental fatigue and working memory load
estimation: Interaction and implications for EEG-
based passive BCI. In Proc. IEEE. Eng. Med. Biol.
Soc. Conf., 6607-6610.
Zhang, D., Tian, X., 2015. How Networked Brain
Changes when Working Memory Load Reaches the
Capacity? In Proc. IEEE. Neural Eng. Conf., 980.983.
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
128
