Transport Planning in Processing Plants for the Fruit Industry

Wladimir E. Soto-Silva

, Marcela C. González-Araya

Lluis M. Pla-Aragones

and Esteve Nadal-Roig

Programa de Doctorado en Ingeniería y Tecnologías de la Información, Universidad de Lleida, Lleida, Spain

Departamento de Ingeniería Industrial, Facultad de Ingeniería, Universidad de Talca,

Camino a Los Niches km 1, Curicó, Chile

Departamento de Matemática, Universidad de Lleida, Lleida, Spain

Keywords: Transportation Planning, Optimization, Fruit Industry, Operational Planning.

Abstract: Processing plants are central for the operation of fruit supply chains. One of the main aspects to consider is

fruit transportation to the processing plant. Hence, this work proposes a mixed integer linear programming

model to support the fruit transport planning from the storage facilities to the processing plant. The aim of

the model is to minimize the daily transportation costs and associated costs of different storage facilities

from where fruits are supplied to the plant in order to meet the demand. The model considers plant

processing capacity, fruit demand, number and type of trucks available and the inventory of fruit in each

type of storage facilities. The model was applied to a real case study of a processing plant located in the

O'Higgins Region (Chile), where reported savings only in transport costs reached about 23 percent.

1 INTRODUCTION

Catalá et al. (2013) agreed that in the recent years,

there has been an increase in the development of

optimization models to support decision making

regarding supply chain management (SCM) in

manufacturing industries. However, this increase in

proposals has not been observed in the agribusiness

sector (Plà et al., 2014). This is also confirmed by

reviews on models applied to the agribusiness sector

done by France and Thornley (1984), Glen (1987),

Lucas and Chhajed (2004), Weintraub and Romero

(2006), Ahumada and Villalobos (2009), Audsley

and Sandars (2009), Bjorndal et al. (2012) and Soto-

Silva et al. (2015).

The review of Ahumada and Villalobos (2009)

presented a classification of optimization models

proposed for the agri-food industry into two

categories: models for perishable agricultural

products (fresh products) and models for non-

perishable products. The fruit industry embraces

both products because as most of the fruit

production is consumed in fresh, there are another

important part processed (e.g canned) and consumed

as long life product.

In supply chains, storage plays an important role;

however, in the supply chain of perishable products,

this activity is critical. Hence, it is common to find

the fruit industry organized as fruit supply chains

with three main stages: production, storing and

processing-distribution (Nadal-Roig and Plà, 2015).

In this regard, Verdouw et al. (2010) stated that the

management of the supply chain of fresh fruit

requires special considerations to maintain freshness

and product quality, involving more limited delivery

times and more controlled storage conditions (low

temperature, less punts, etc.). Farmers perform

actions to minimize losses due to quality

deterioration like cool storage. Pittia et al. (1999)

and McHugh and Senesi (2000) discussed different

techniques of preserving the raw material quality

over time. These techniques refer to microbiological

and blanching treatments for preserving fruit quality

in cold storages facilities.

The development of optimization models to

support fruit supply chain management and

coordination, Blanco et al. (2005) presented a model

for production scheduling in an apples and pears

packing plant. The authors proposed a mixed integer

programming model to plan the production process,

in order to maximize profit estimated by fruit sale

incomes less raw material purchase, cold storage and

labor costs. As result, an annual schedule

considering packaging plant constraints was

Soto-Silva, W., González-Araya, M., Pla-Aragones, L. and Nadal-Roig, E.

Transport Planning in Processing Plants for the Fruit Industry.

DOI: 10.5220/0005646100710078

In Proceedings of 5th the International Conference on Operations Research and Enter prise Systems (ICORES 2016), pages 71-78

ISBN: 978-989-758-171-7

developed. In a related research, Blackburn and

Scudder (2009) presented a mathematical model to

determine the loss in value of perishable agricultural

products depending on the type of storage. This

research corroborated that cold storages allow fruit

industry for a better fruit quality during postharvest.

In the literature, there are also optimization

models to support decisions in distribution and

transportation for supply chains of perishable and

non-perishable agricultural products. For instance,

Mula et al. (2006) and Mula et al. (2010) presented

reviews of the different optimization models applied

to transportation planning in supply chains. More

recently, Nadal-Roig and Plà (2015) proposed a

linear programming model that minimizes the

associated costs to transport from cooperatives to a

fruit logistic center. The model scheduled the daily

transport routes in order to satisfy the demand of the

logistic center, at a minimal cost. Furthermore, the

authors emphasized another complex task in fruit

supply chain like the planning and coordination of

different agents involved in production, processing,

storage and distribution.

Thus, it seems from literature that managing fruit

storages of different types and the coordination of a

fruit supply chain requires a sound transport

planning. Currently, optimization models to decision

support for daily transportation planning from

warehouses or storage centers, with different types

of cold storages, to the processing plants has not

been yet proposed. Even less, there are such

optimization models used in practice to the

knowledge of authors. Surprisingly, transportation

models for nearby industries of the primary sector

like forestry (Weintraub et al., 1996) or sugar

industry (Lopez-Milan and Plà-Aragonés, 2014)

have been developed successfully, but not to the

fruit industry (Oliva, 2011). So that, to cover this

gap in this paper, a mixed integer linear

programming model to find the optimal transport

planning from warehouses with different cooling

technologies to a fruit processing plant is proposed.

The model minimizes the total cost associated with

transport and proposes the opening of the cold

storage facilities grouped in warehouses. Finally,

we applied the model to a real case study in a

processing plant of Japanese plums and canned

peaches.

Therefore, this paper is structured as follows. In

section 2, the description of the problem of transport

and storage in Chile is presented. In section 3, the

proposed mathematical model for transportation

planning in the fruit industry is presented. In section

4, a case study obtained from a Chilean company for

establishing fruit transportation planning is carried

out. In section 5 are presented the conclusions as

well as further research.

2 FRUIT STORAGE AND

TRANSPORT TO PROCESSING

PLANTS

The planning and coordination of different agents

involved in production, processing, storage and

distribution are unavoidable tasks in a fruit supply

chain. In the network of fruit supply chains, each

stakeholders transport the fruit downstream to the

next level in the chain. The activities developed at

each level are briefly described below.

Harvesting is done by producers who are

generally the farms’ owners. Crops are collected

using containers, which are transported from the

farm to the storage facilities (cold storages), or

directly to the process plant. Note that the plant is

responsible for assigning the fruit destination. Each

plant purchases the fruits and takes care of his

retirement from the orchards.

The storage time depends on the fruit and

variety. For example, apples and pears, depending

on the variety, may be stored for up to 9 months. On

the contrary, cherries are not stored. They must be

processed the same day they are harvested.

However, for all stored fruit, the cooling system

must be considered to control the ripening process of

these (Nadal-Roig and Plà, 2015).

Processing is performed in processing plants

with a different degree of complexity. The simplest

process is exhibited in packing plants where fruit is

intended for fresh consumption. Minimal processing

is gaining popularity as a way to diversify the

production offered to the market.

Retailing varies depending on product quality,

added value and amount sent to the market.

Although the usual way is that retailing firms place

orders to processing plants and distribute the fruit

among consumers, it is also common for small and

local production the access to the market from

storage facilities hold by producers.

In general, the fresh fruit arrives to processing

plants from different cold storage facilities,

according to the plants and retail demands. So, an

important issue for managers is to decide which and

when a cold storage facility must be opened in order

to pick the fruit up for satisfying the demands. This

decision depends on the stored fruit and technology

of the cold storage facilities.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

The structure of the fruit supply chain can have

different configurations, but the basic elements

inherent in the stakeholders remain the same

(Verdouw et al., 2010). For example, at the bottom

of the fruit supply chain in Chile are the farmers,

who sell their products to processing plants. The

processing plants either store the fruit in storage

centers (which are owned or rented) or process the

fruit immediately in the plant. This approach is

different from other countries like Spain, where

farmers usually are grouped in cooperatives owning

storages centers supplying to the processing plants.

In this case, there is not a change of ownership for

the fruit, because these stages are managed by a

cooperative of producers integrated in a sole

company.

Different types of cold storage facility are

available, and these are: the Conventional Cold

technology storage facility (CC), where the

temperature control is performed by a thermostat,

thereby maintaining the fruit for a period

approximately of 3 months; The Smart Fresh

technology storage facility (SF), which has a built-

diffusion system phytoregulator for protecting the

fruit from the effects of ethylene during storage,

allowing the fruit to maintain a period approximately

of 6 months; and Controlled Atmosphere technology

storage facility (CA), where the concentrations of

oxygen, carbon dioxide and nitrogen are controlled

as well as the temperature and humidity. That is, the

atmosphere in the storage facility is controlled,

thereby maintaining the fruit for a period

approximately of 9 months. Generally, plants have

more storage, in order to have fruit for processing

throughout the year. There is also possible some

changes between types of storages. For instance, the

transformation of a conventional cold storage

facility into a Smart Fresh depends on the demand

and need for each company according to their

estimated time of fruit supply.

In Chile, in each cold storage facility is only

possible to store one type of fruit at a time (Oliva,

2011). According to the Center for Natural Resource

Information (CIREN, 2005), in 2004, Chile had

approximately 201 agro-companies and 2,349 cold

storage facilities.

Quite often, the fruit transportation from

warehouses is coordinated by processing plants to

satisfy subsequently the orders they receive at the

same time from retailers. This transport must be

planned according to the availability of trucks and /

or drivers (Hsiao et al., 2010), in order to meet the

demand of different varieties. Also, it is important to

consider daily variations of processed fruit

quantities, because of unforeseen changes in demand

or in order priorities. Moreover for the fruit

transportation, a fleet of trucks is rent and the

payment thereof is made according to the number of

daily trips made. On the other hand, the availability

of a fixed number of trucks is necessary to ensure a

minimum and maximum number of daily (Oliva,

2011).

3 MODEL FOR PLANNING THE

DAILY TRANSPORTATION

STORAGE FACILITIES TO

THE PROCESSING PLANTS

The formulation of the proposed model for planning

the daily transport from the storage facilities to

processing plants model is presented. The indices,

parameters and decision variables of the model can

be found in the Appendix.

Mathematical formulation





















































(1)

s.t













∀,



.



(2)

















∀  , ,.

(3)















∀

(4)







  ∀  ,.

(5)











∀.

(6)











∀.

(7)

Transport Planning in Processing Plants for the Fruit Industry













∀, 





.

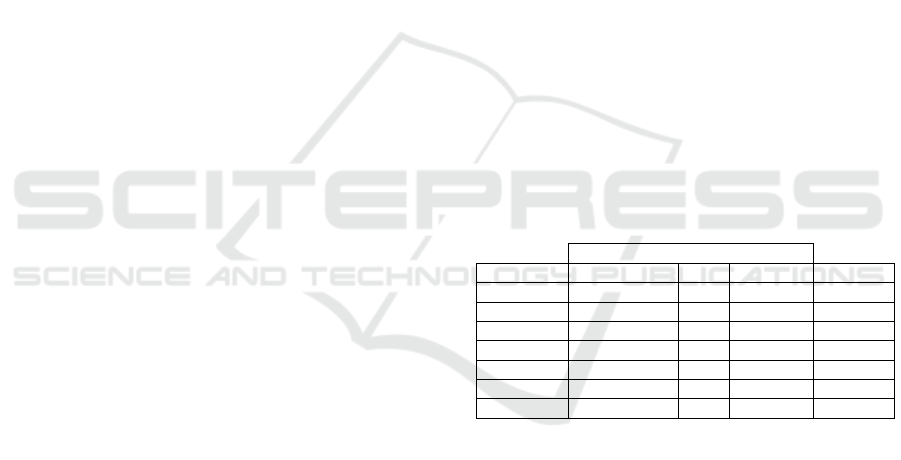
(8)







 0∀,





,.

(9)





Ζ



∀,,.

(10)

The objective function minimizes the costs

associated with transport from cold storage to

processing plants and the fixed costs for the opening

of the different types of storage facilities. Thus, the

objective function can be decomposed as follows:

Minimize: transportation cost + fixed cost for

opening conventional cold storage facilities + fixed

cost for opening Smart Fresh storage facilities +

fixed cost for opening controlled atmosphere storage

facilities.

The aim of the fixed costs is to prioritize the

quality of the fruit to be processed, where the

technology of cold storage facility opening is

relevant. For this reason, the model has to consider

that in conventional cold storage facilities fruit

quality deteriorates before than fruits stored in

controlled atmosphere. Thus, the fixed for opening

conventional cold storage facilities is lower than that

for Fresh and controlled atmosphere. Likewise, fixed

for opening Smart Fresh storage facilities is lower

than that for controlled atmosphere.

Constraint (2) states that the amount of fruit

removed from storages by trucks should be greater

than or equal to processing plant demand. Constraint

(3) restricts the amount of fruit transported daily

from a warehouse to a plant by a truck must be less

or equal to the capacity of the truck by the number

of trips made on the day between the warehouse and

plant. Constraint (4) shows that each truck must not

exceed the maximum number of usage hours. The

ivp

parameter counts the total hours of a trip

between a warehouse and a plant, where it is

considered the truck travel time, holding time, the

loading and unloading time in both the plant and

store. The restriction (5) shows that must not exceed

a certain amount of trips per each truck, between a

store and a plant, because the production capacity of

the plants. Constraint (6) limits the maximum

number of truck trips and the constraint (7) limits the

minimum number of truck trips. Thus, the

constraints 6 and 7 balance the number of trips that

can make the trucks and therefore, maintaining a

fixed number of trucks available for transportation

daily. Constraint (8) states that shipped weight in kg

for a certain kind of fruit to a processing plant, from

a particular cold storage must be less or equal to the

stock of fruit available. Constraints (9) and (10)

correspond to no negativity and integrality of the

decision variables, respectively.

4 CASE STUDY OF A CHILEAN

COMPANY

The studied company is currently one of the fruit

leading exporters of Chile. Their orchards are

located in the Metropolitan Region and the Region

of O'Higgins.

The company stores two types of fruits in cold,

with these Japanese plums and canning peaches.

In 2013, a total of 642.0 t of Japanese plums and

9392.2 t of canning peaches stored in cold storage

facilities, which must be transported during the

season to the plant for processing. In addition, the

company has six warehouses with 62 cold storage

facilities, of which 23 have a capacity of 400 bins,

30 have a capacity of 600 bins, and nine have a

capacity of 1000 bins. It should be noted that one bin

is a reservoir with a capacity of about 400 kg. The

distribution of cold storage in warehouses according

to their cold technology is presented in Table 1.

Table 1: Number of cold storage facilities in the

warehouses according to its technology.

Storage facilities’ type

Warehouse CC SF CA Total

#1 5 - - 5

#2 2 8 - 10

#3 - 4 - 4

#4 2 7 6 15

#5 2 2 2 6

#6 10 6 6 22

Total 21 27 14 62

As it is seen in Table 1, the company has 21 CC

storage facilities (Conventional Cold), 27 SF storage

facilities (Smart Fresh) and 14 CA storage facilities

(Controlled Atmosphere). The company performs

the distribution of the fruit to cold storage

warehouses, based on the experience of the charge

of the process, taking into account the distance

between each field and warehouse, plus the

availability of cold storage facilities.

For the transportation of fruit, the company has

four trucks. These trucks are assigned to different

warehouses based on the experience of the plant

manager and production manager of the company.

Transportation decisions to the plant are made

daily, based on the orders of costumers accepted for

the day. Three different instances are considered for

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

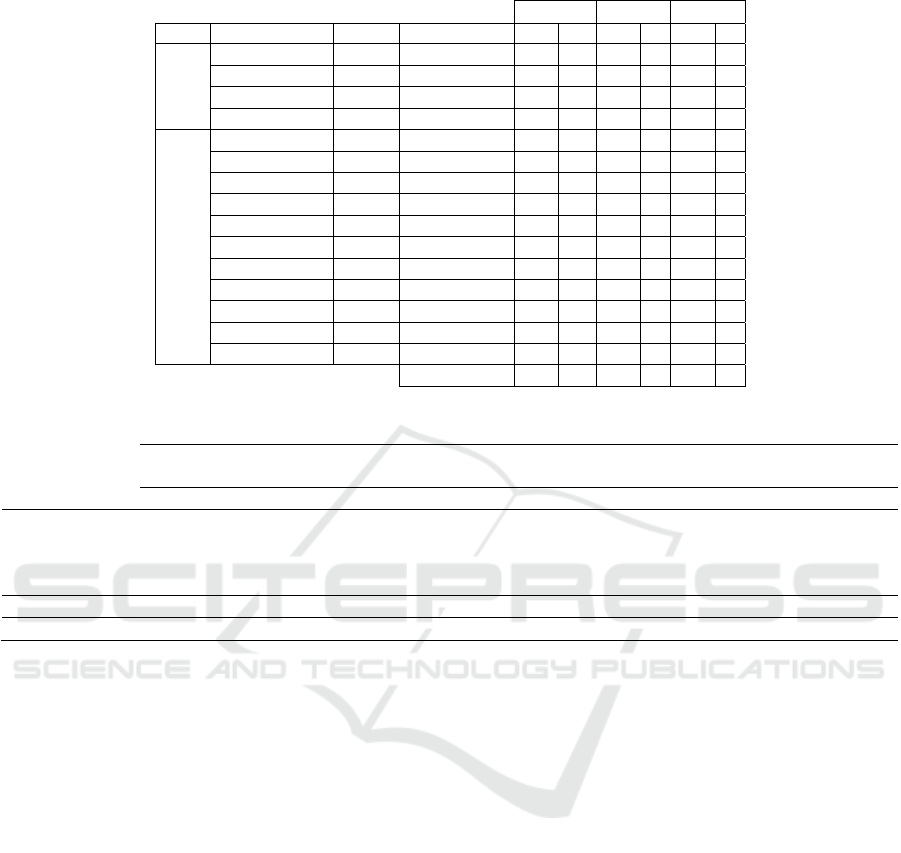
Table 2: Processing plant demands for each analyzed day.

Day 0 Day 30 Day 90

Fruit Type Variety Variety Bins t Bins t Bins t

Plum

Japanese plums

Angeleno 80 32 0 0 0 0

Japanese plums

Black Diamond 0 0 0 0 0 0

Japanese plums

Larry Anne 0 0 0 0 0 0

Japanese plums

Saphiro 0 0 0 0 0 0

Peach

Canning peaches

Andross 40 16 80 32 50 20

Canning peaches

Ross Peach 20 8 40 16 30 12

Canning peaches

Loadell 0 0 0 0 25 10

Canning peaches

Bowen 0 0 40 16 40 16

Canning peaches

Carson 40 16 35 14 35 14

Canning peaches

V10

Klampt 40 16 0 0 0 0

Canning peaches

V11

Everst 0 0 0 0 20 8

Canning peaches

V12

Hesse 0 0 15 6 15 6

Canning peaches

V13

Kakama 0 0 0 0 0 0

Canning peaches

V14

Tirrenia 40 16 0 0 0 0

Canning peaches

V15

Rizzi 0 0 0 0 0 0

Total 260 104 210 84 215 86

Table 3: Scheduled trips from the warehouses to processing for each analyzed day.

Day 0 Day 30 Day 90

Truck Truck Truck

From

# 1 # 2 # 3 # 4 # 1 # 2 # 3 # 4 # 1 # 2 # 3 # 4

W1 0 1 1 0 1 1 0 0 0 1 0 0

W4 2 0 0 0 2 0 0 0 2 0 0 0

W5 0 0 0 1 0 0 1 1 0 0 0 1

W6 2 0 0 0 0 0 0 0 0 0 1 0

# Trips

4 1 1 1 3 1 1 1 2 1 1 1

Tons

41.6 12.8 26.4 23.2 31.2 11.6 14.8 26.4 20.8 12.8 26.0 26.4

the analysis of the case study. These instances

correspond to the production planning of the

processing plant in three different days. The first

instance is the starting day of the processing fruit

period, day 0, where all the stock is available. For

the second instance, we consider the data of the day

after the beginning of operations at the plant. At

this time, the stock of stored fruit has decreased a

25%. The third instance is the day 90

after the

beginning of operations at the plant. At this time,

fruit available in cold storage has decreased a 59%

compared to the beginning of the season.

In Table 2, the demands of the plant for each

fruit varieties are presented in each of the proposed

instances (analyzed days).

As it is seen in Table 2, the first instance (day 0)

has a demand of 104 t, and 6 varieties of fruit are

claimed. In the second instance (day 30) the demand

is 84 t, where five types of fruit are demanded, and

in the third instance (day 90) has a demand of 86 t,

with a demand of 7 varieties of fruit.

Note that in all three scenarios some of the

varieties of fruit were not shipped, because in the

days analyzed were not required. However, these

varieties were required on other days during

planning.

The number of trips by trucks and the

warehouses which trucks should be directed are

presented in Table 3.

As it is seen in Table 3, a total of 7, 6 and 5 trips

to the processing plant are required at day 0, 30 and

90 respectively. Considering the three instances, the

truck #1 (truck type 1) is always performing most of

the trips representing the 40%, 37% and 24% of the

total number of tons transported at day 0, 30 and 90

respectively. The results concerning to the number

of fruit tons to be transported from different

warehouses to the processing plant in each truck are

presented in Table 4.

As it is seen in Table 4, 104.0 t are transported

from the storage facilities to the processing plant at

day 0, satisfying the demand of each of the varieties.

The model aims to use the fruit for those storage

facilities whose are Conventional Cold type (CC),

opening 5 cold storage facilities of this type,

followed by the opening of Smart Fresh (SF) 3

storage facilities, and finally, gives 1 controlled

atmosphere (CA) storage facilities, just to minimize

Transport Planning in Processing Plants for the Fruit Industry

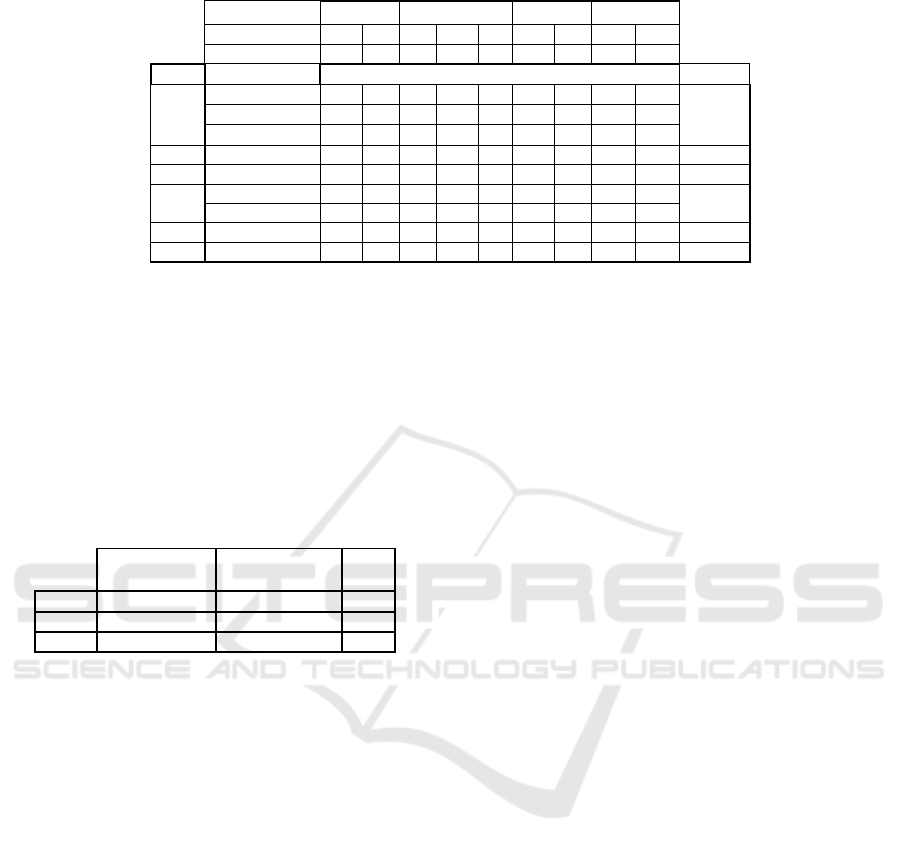
Table 4: Transport planning from warehouses to processing plant at day 0.

Warehouse W1 W4 W 5 W 6

Type CC CC CC SF SF SF CA CC CC

Cold Storage # 1 5 20 22 25 37 40 43 46

Variety Truck #

Total (t)

# 1 - - 0.8 - - - - - -

32.0

# 2 12.8 - - - - - - - -

# 3 18.4 - - - - - - - -

# 4 - - - - - 16.0 - - - 16.0

# 3 - 8.0 - - - - - - - 8.0

# 1 - - - - 4.0 - - - 4.8

16.0

# 4 - - - - - - 7.2 - -

V10

# 1 - - - 16.0 - - - - - 16.0

V14

# 1 - - - - - - - 16.0 - 16.0

the fixed costs of opening of different types of cold

storage facilities. The opening of the CA storage

facilities is influenced because the demand for the

variety of fruit could not be satisfied with that was

stored in the standard CC and SF storage facilities.

In relation to transport costs and fixed opening costs

of cold storage, in Table 5 the results for the three

instances studied are presented.

Table 5: Transportation costs and opening fixed costs of

cold storage facilities (in $USD*).

Transportation

costs

Storage facility

opening fixed

Total

cost

Day 0

317 91

408

Day 30

244 93

337

Day 90

285 104

389

* 1 USD = 555.15 CLP, exchange rate in February 21st of 2014

(www.bcentral.cl).

Note that the instances (days 0, 30 and 90) are

real cases in the processing plant, so that the demand

and stocks at the beginning of the day are real for the

company.

Comparing the cost of transportation plans

derived from the optimal solution of each instance

versus actual planning that took place at each

studied day in the company, the first instance

reported savings of 22%, in the second scenario

savings of 26% and in the third scenario 20% saving

respectively representing an average savings of 23%

during the season.

5 CONCLUSIONS

In this research, a mathematical optimization model

with the aim to plan the daily transport from the

storage centers in the fruit processing plant,

minimizing the costs associated with transport is

presented. The model also performs an optimal

opening of the storage facilities depending on the

type presented technology associated with the

cooling of each of them. The processing plant makes

both its own and leased storage to have fruit

throughout the season progresses and thereby meets

demand.

For the Chilean case, it is important to segment

the cold storage facilities according the cool

technology, since a plan about what cold storage

facilities will be opened first for the season, in order

to ensure the quality of the fruit that is sent to

process is needed. The mathematical formulation

presented by Nadal-Roig and Plà (2015) is the basis

for the extension developed in this paper where

various processing plants and different types of

storing facilities are considered.

As the model is intended for practical use, the

computational performance of the model is analyzed

under two scenarios in which the amount of storage

centers, trucks fleet, demand, availability of fruit in

cold storage and quantity of plants vary, obtaining

the optimal solution in both cases. For the smaller

scenario (6 warehouses, 62 cold storage facilities

with 10 million kilos of stored fruit and a processing

plant), the model provided the optimal solution after

10 seconds, while for the scenario where the

parameters mentioned increased twice, the optimal

solution was reached in 3600 seconds. This shows

that for the more complex cases that could be

expected in the Chilean fruit industry, it would be

possible to deliver an optimal solution in a

reasonable computational time.

Finally, the model is applied to a real case of a

fruit processing plant in the O'Higgins Region,

Chile, which has 62 cold storage facilities, grouped

into 6 warehouses. The company processes varieties

of peaches and plums, having a total of 15 varieties.

Each season holds approximately 10 million kilos of

fruit. The model, when applied to three days

observed in the 2013 season, achieved cost savings

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

average transport of about 23 percent relative to the

value observed transport cost. Regarding the

reduction in the costs of opening cold storage, it has

been possible to demonstrate the solution delivered

by the model is consistent with the priority

established in practice for opening storage facilities.

Future extensions of the model are exploring to

incorporate the temporary nature in the transport

planning, i.e. including tactical decisions like the

transportation planning for the entire season. Hence,

the optimal size of the fleet could be assessed. This

research would require good estimates of both truck

type’s characteristics and the demand for each

variety of fruit to be processed in a season.

Finally, it would be interesting to integrate this

model into existing mathematical models that

consider operations in the orchards or the filling of

different types of cold storage, depending on the

quality of harvested fruit.

REFERENCES

Audsley, E. & Sandars, D.L. (2009) A review of the

practice and achievements from 50 years of applying

OR to agricultural systems in Britain. OR Insight.

22(1). p.2–18.

Ahumada, O. & Villalobos, J.R. (2009) Application of

planning models in the agrifood supply chain: A

review. European Journal of Operational Research.

195. p.1-20.

Bjorndal, T., Herrero, I., Newman, A., Romero, C. &

Weintraub, A. (2012) Operations research in the

natural resource industry. International Transactions

in Operational Research. 19 (1-2). p. 39-62.

Blanco, A., Masini, G., Petracci, N. & Bandoni, J. (2005)

Operations management of a packaging plant in the

fruit industry. Journal of Food Engineering. 70.

p.299–307.

Blackburn, J. & Scudder, G. (2009) Supply Chain

Strategies for Perishable Products: The Case of Fresh

Produce. Production and Operations Management.

18(2). p.129–137.

Catalá, L.P., Durand, G.A., Blanco, A.M. & Bandoni, J.A.

(2013) Mathematical model for strategic planning

optimization in the pome fruit industry. Agricultural

Systems. 115. p.63-71.

CIREN – Centro de Información de Recursos Naturales

(2005). Report N°4: Storage Cold Capacity in Fruit

Industry. In Spanish. Download from the link:

http://bibliotecadigital.ciren.cl/gsdlexterna/collect/bdir

enci/index/assoc/HASH01ba.dir/bolfrut4.pdf.

France, J. & Thornley, J. (1984) Mathematical Models in

Agriculture. London: Butterworths.

Glen, J. (1987) Mathematical Models in Farm Planning: a

survey. Operations Research. 35 (5). p.64-665.

Hsiao, H.I., Kemp, R.G.M., van der Vorst, J.G.A.J. &

Omta, S.W.F. (2010) A classification of logistic

outsourcing levels and their impact on service

performance: Evidence from the food processing

industry. International Journal of Production

Economics. 124. p.75-86.

Lopez-Milan, E. & Plà-Aragonés, L.M. (2014) An

Operational Computerised System to Manage the

Supply Chain of Sugar Cane. Annals of Operations

Research. 219. p.285-297.

Lucas M, Chhajed D (2004) Applications of location

analysis in agriculture: a survey. J. Oper. Res. Soc. 55:

561–578.

Mchugh A, Senesi R (2000) Apple Wraps: A Novel

Method to Improve the Quality and Extend the Shelf

Life of Fresh-cut Apples. Journal Food. Sci. 65(3):

480–485.

Mula J, Poler R, Garcıa-Sabater J, Lario F (2006) Models

for production planning under uncertainty: A review.

Int. J. Prod. Econ. 103: 271–285.

Mula J, Peidro DD, Vicens E (2010) Mathematical

programming models for supply chain production and

transport planning. Eur. J. Oper. Res. 204:377-390.

Nadal-Roig E, Plà L (2015) Optimal transport planning for

the supply to a fruit logistic center. In: Plà-Aragonés,

L.M. (Ed.) Handbook of Operations Research in

Agriculture and the Agri-Food Industry. Springer-

Verlag. In press.

Oliva M (2011) Optimization Model for Agribusiness’

Apple Supply Chain. Master Thesis Dissertation,

Programa de Magíster en Gestión de Operaciones,

Facultad de Ingeniería. Universidad de Talca. In

Spanish.

Plà LM, Sandars D, Higgins A (2014) A perspective on

Operational Research prospects for agriculture. J.

Oper. Res. Soc. 65: 1078–1089.

doi:10.1057/jors.2013.45.

Pittia P, Nicoli M, Comi G, Massini R (1999) Shelf-life

extension of fresh-like ready-to-use pear cubes. J. Sci.

Food Agr. 79: 955–960.

Soto-Silva W, Nadal–Roig E, Gonzalez–Araya M, Plà-

Aragones L (2015) Operational Research Models

Applied to the Fresh Fruit Supply Chain. Accepted to

Eur. J. Oper. Res. DOI: 10.1016/j.ejor.2015.08.046.

Verdouw N, Beulens A, Trienekens J, Wolfert J (2010)

Process modelling in demand-driven supply chains: A

reference model for the fruit industry. Comput.

Electron. Agr. 73: 174–187.

Weintraub A, Romero C (2006) Operations Research

Models and the Management of Agricultural and

Forestry Resources: A Review and Comparison.

Interfaces: 46(5): 446-457.

Weintraub A, Epstein R, Morales J, Serón J, Traverso P

(1996) A truck scheduling system improves efficiency

in the Forest industries. Interfaces 26(4): 1–12.

APPENDIX

Sets, parameters and variables used in the

Transport Planning in Processing Plants for the Fruit Industry

formulation

The sets used by the model are the following:

P: Processing plants set.

F: Varieties of fruit stored in different storage

facilities available for the storage of products.

V: Set of trucks available.

I: Set of storages available for the fruit

: Set of Conventional Cold storage facilities in the

storage i

: Set of ‘Smart Fresh’ storage facilities in the

storage i

: Set of Controlled Atmosphere in the storage i.

: C

U C

: Set of storage facilities in the

storage i

The parameters considered by the model are the

following:

: Fuit demand f, fF, from the processing plant p,

p P.

: Maximum capacity for the truck v, vV.

ivp

: Travel time that warehouse i, i



I, with the

truck v, v



V, with destination to the processing

plant p, p



: Maximum number of hours of driving for the

truck v, vV.

: Maximum number of trip for the truck v, vV.

: Minimum number of trip for the truck v, vV.

: Opening fixed cost for the storage facilities type

f (Type CC: Conventional cold).

: Opening fixed cost for the storage facilities type

s (Type SF: Smart Fresh).

: Opening fixed cost for the storage facility type a

(Type CA: Controlled atmosphere).

ivp

: Transportation cost from the warehouse i, i



with the truck v, v



V, with destination to the

processing plant p, p



N: Number of trucks allowed removing fruit to the

warehouses

icv

: Stock available in the storage i, and storage

facility c, c



, of the fruit f, f



The decision variables of the model are the

following:

icvfp

: kg transported from the storage i, from the

storage facility c, c



, and fruit type v, v



and truck f, f



F, with destination to the

processing plant p, p P.

ivp

= Number of trips from the storage i done by the

truck v,v



V, to the processing plant p, p



ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems