Generating Metamodel Instances Satisfying Coverage Criteria via SMT
Solving
Hao Wu
Computer Science Department, National University of Ireland, Maynooth, Republic of Ireland
Keywords:
Metamodel, Satisfiability Modulo Theories (SMT), Coverage Criteria, Graph.
Abstract:
One of the challenges for using metamodels in Model Driven Engineering is to automatically generate meta-
model instances. Each instance should satisfy many constraints defined by a metamodel. Such instances
can then be used for verifying or validating metamodels. Recent studies have already shown that this can be
tackled by using SAT/SMT solvers. However, such instance generation does not take coverage criteria into
account, and instances satisfying specified coverage criteria could be useful for testing model transformation.
In this paper, we present an approach consisting of two techniques for coverage oriented metamodel instance
generation. The first technique realises the standard coverage criteria defined for UML class diagrams, while
the second technique focuses on generating instances satisfying graph-based criteria. With our approach, both
kinds of criteria are translated to SMT formulas which are then investigated by an SMT solver. Each success-
ful assignment is then interpreted as a metamodel instance that provably satisfies a coverage criteria or a graph
property. We have already integrated this approach into our existing tool to demonstrate the feasibility.
1 INTRODUCTION
A model provides a representation of aspects of a sys-
tem. This can include design models such as UML
class or sequence diagrams, or implementation mod-
els, such as source code in a programming language.
A metamodel is a model that is used to describe the
structure of other models, modelling languages or do-
main specific languages. Each instance of a meta-
model is then a model that can be regarded as a test
case. These test cases are important not just for val-
idating a metamodel itself, but also useful for testing
the tools and frameworks that process the models de-
fined by that metamodel such as model transofrma-
tion.
For example, given a domain specific language L,
say, a metamodel would usually define the abstract
syntax and static semantics of the language. A typical
representation of the metamodel would be as a UML
class diagram (using a subset of the constructs) with
constraints specified using the Object Constraint Lan-
guage (OCL). A set of instances of this metamodel
would be programs written in language L, and would
allow language engineers to check that they had spec-
ified the relevant constructs correctly.
A number of approaches and tools have already
provided a way of generating these instances (Ehrig
et al., 2009; Gonz
´
alez P
´
erez et al., 2012; Cabot et al.,
2014). However, these instances are not measured
via any criteria. At least, meeting some criteria such
as standard coverage criteria for UML class diagram
would help users to increase their confidence in de-
signing or validating metamodels. Furthermore, users
may also wish to generate instances that possess cer-
tain coverage metrics for other testing purposes such
as using depth of inheritance tree for testing inher-
itance relationships. Thus, naively generating in-
stances from a metamodel without taking account of
coverage criteria or other properties is not very ade-
quate.
This paper addresses the issue of generating meta-
model instances satisfying coverage criteria. More
specifically, this paper makes the following contribu-
tions:
• A technique that enables metamodel instances to
be generated so that they satisfy partition-based
coverage criteria.
• A technique for generating metamodel instances
which satisfy graph properties.
Both two techniques that encode coverage criteria and
graph properties into a set of SMT formulas. These
formulas are then combined with the formulas gener-
ated from our previous work, and solved by using an
40
Wu, H.
Generating Metamodel Instances Satisfying Coverage Criteria via SMT Solving.
DOI: 10.5220/0005650000400051
In Proceedings of the 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2016), pages 40-51
ISBN: 978-989-758-168-7
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

external SMT solver (Wu et al., 2013). Each success-
ful assignment for the formulas is interpreted as an in-
stance. We have already automated this process into
a tool to demonstrate the feasibility of this approach.
2 BACKGROUND
In this section, we briefly review the standard cover-
age criteria defined for UML class diagram, notations
we use for expressing a metamodel as a graph, and
basic SMT encodings from our previous work. For-
mally, we consider all metamodels in this paper as
being presented as UML class diagrams, and repre-
sented as graphs.
2.1 Metamodel Coverage Criteria
A metamodel is a structural diagram and can be de-
picted using the UML class diagram notation. Thus,
the coverage criteria defined for UML class diagram
can also be borrowed for metamodels. In particular,
we focus on the coverage criteria presented in (An-
drews et al., 2003) (Ghosh et al., 2003), especially the
work focused on testing the structural elements of a
UML class diagram. These coverage criteria are stan-
dard criteria for testing a UML class diagram and they
are defined as follows:
• Generalisation coverage (GN) which describes
how to measure inheritance relationships.
• Association-end multiplicity coverage (AEM)
which measures association relationships defined
between classes.
• Class attribute coverage (CA) which measures the
set of representative attribute value combinations
in each instance of class.
AEM and CA are partition-based testing criteria
which means that testing results depend on the choice
of a representative value from each partition (Ostrand
and Balcer, 1988). Therefore, the value domain is
partitioned into several equivalence classes, and each
value from an equivalent class is expected to have the
same results. The partitions can also be decided using
domain knowledge-based partitioning.
For example, to satisfy the CA criterion for the
metamodel in Figure 1, we may assume a user could
choose a representative value of 18
1
, and this allows
the attribute age in the abstract class Person to be di-
vided into 3 partitions which are 18 < age, age = 18
and age > 18. The hypothesis is that any single value
1
A user may choose a different representative value, this
depends on the knowledge about a specific domain.
from one of the three partitions is expected to have the
same results for all other values from that partition
(Myers and Sandler, 2004). Similarly, to satisfy the
AEM criterion, the binary association (employees) in
the metamodel can also be divided into two partitions:
a Department that has no Manager or a Department
that has multiple Managers. The multiple number
of Managers can be a boundary value chosen by a
user. For example, it can be the maximum value that
an integer can hold or 5 if it is determined by spe-
cific domain knowledge about the model. Finally, to
satisfy the GN criterion, the inheritance relation can
be covered by ensuring the creation of an instance of
Manager.
In this paper, we focus on generating instances
meeting CA and AEM criteria by providing a general
SMT encoding. For GN, it has already been incorpo-
rated into our previous work. Our previous work takes
a metamodel, presented as a class diagram with OCL
constraints, augmented with quantitative constraints,
and uses an SMT solver to generate instances. Our
earlier work also supports a subset of OCL, this in-
cludes: constraints on an attribute, navigation over an
association, and nested quantifiers over a collection of
instances. To facilitate the transformation from class
diagrams with OCL constraints to SMT formulas we
use a bounded typed graph as an intermediate repre-
sentation.
2.2 Bounded Typed Graphs
Our previous work considered classes in a metamodel
as nodes, and relationships between classes are edges
linking one node to another (Wu et al., 2013). Thus,
we can formally define a graph, namely typed graph
(T G) as: T G = (V
T
,E
T
), where V
T
and E
T
represents
a set of nodes (classes) or edges (associations and in-
heritances).
Each valid instance of a metamodel is also a
graph: G = (V
G
,E
G
), where V
G
is set of nodes (ob-
jects) and E
G
is set of edges (links), but preserve
extra type information about the classes in a meta-
model. Thus, we now can define a mapping between
two graphs T G and G: type = (type
V
,type
E
) where
type
V
: V
G
→ V
T
and type
E
: E
G
→ E
T
.
Now, we formally define a bounded typed graph
as: T G
b
= (V
T
,E
T
,b) where b is a bound function
b : V
T
→ Z
+
that maps a typed node (non-abstract)
to an integer. This integer specifies an upper bound
of the same typed node that an instance may con-
tain. Therefore, using this bound function, we can
bound our search space to guarantee the termination
for metamodel instance generation.
For example, Figure 1 and 2 show a meta-
Generating Metamodel Instances Satisfying Coverage Criteria via SMT Solving
41

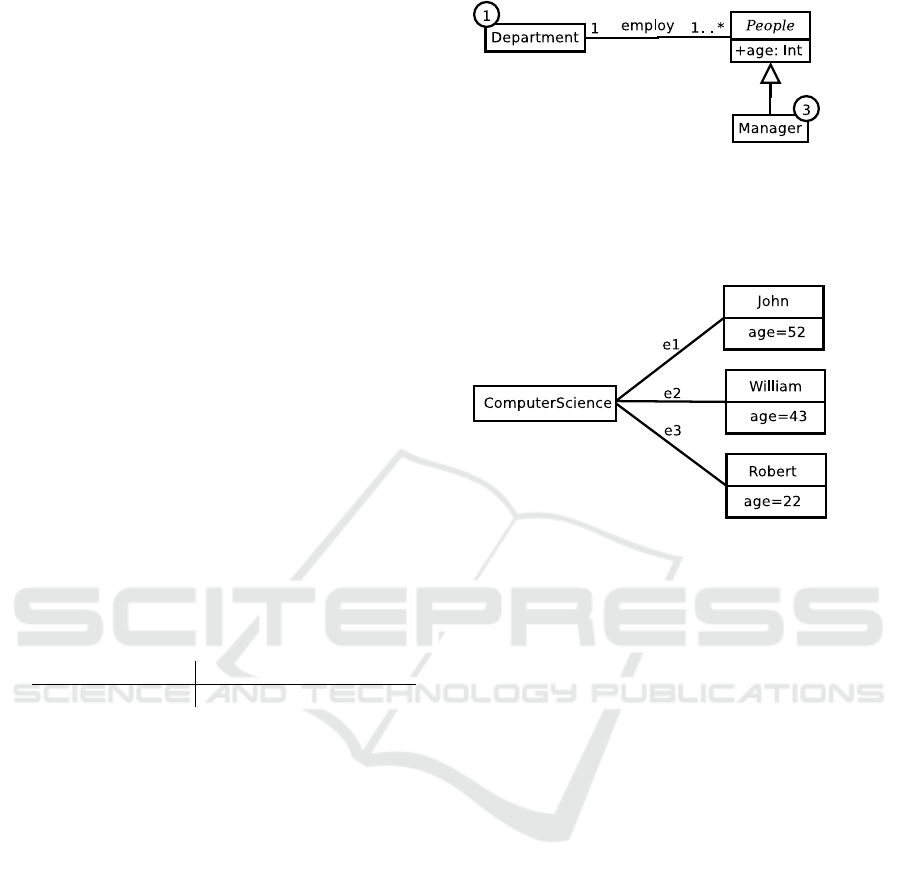
model represented as a bounded typed graph and
an instance of it. The bounded typed graph
(metamodel) and graph (model) can be related
with type such that type
V
(ComputerScience) =
Department, and type
V
(John) = type
V
(Willam) =
type
V
(Robert) = Manager. Similarly,type
E
(e1) =
type
E
(e2) = employ.
To generate valid instances from a metamodel, we
form a finite universe based on each bound defined
for a typed node. This includes generating all pos-
sible links based on a particular association (edge)
defined within the bound. We then use correspond-
ing translation rules to encode them into SMT for-
mulas. For example, for the typed graph shown
in Figure 1, we form a finite universe containing
1 Department (ComputerScience) and 3 Managers
(John,William,Robert). For the association employ,
we form an adjacent matrix that describes all possi-
ble connections between Department and Manager.
Each entry in the matrix is an SMT boolean variable
indicating whether a link is selected or not. We then
disjunct each entry in the matrix. The following steps
show this basic translation for the metamodel in Fig-
ure 1 to the SMT formulas:
1. Form a finite universe:
{ComputerScience,John,William, Robert}
2. For association employ, we form an adjacency
matrix:
John William Robert
ComputerScience e
1
e
2
e
3
3. Generate SMT formula: e
1
∨ e
2
∨ e
3
The SMT formula captures the meaning of associa-
tion employ: each Department is associated with at
least one of the Mangers. Figure 2 shows an exam-
ple of only e
1
, e
2
and e
3
are assigned to be true by an
SMT solver, representing John, William and Robert
are employed by the ComputerScience department.
In this paper, we assume all OCL constraints de-
fined over a metamodel are not conflicted with both
criteria. For example, a representative value of 18 is
chosen for the attribute age, and an OCL constraint is
defined as sel f .age <> 18.
3 PARTITION-BASED INSTANCE
GENERATION
The main idea for generating instances that satisfying
CA and AEM coverage criteria is by adding additional
constraints expressed as SMT formulas to block ir-
relevant instances during the search. Each successful
Figure 1: An example of a metamodel, represented as a
bounded typed graph. The bounds for Department and
Manager are depicted with a number in a circle on each
class. In this case, they are 1 and 3 for Department and
Manager respectively. No bound is specified for People as
it is an abstract class.
Figure 2: An instance of metamodel in Figure 1. This in-
stance contains 1 instance of department and 3 instances of
manger.
assignment is then interpreted as an instance that sat-
isfies the coverage criteria. In the following sections,
we show how these constraints can be expressed as
SMT formulas.
For the set of features P in a metamodel, the gen-
eral form of a constraint for each feature P
i
in P can
be expressed by:
|P
i
|
_
j=1
(T
i
= V
j
) ∧ F
i
where
• |P
i
| denotes the total number of partitions of a fea-
ture P
i
.
• T
i
is a partition switch, determines when a partic-
ular partition is to be switched on or off based on
V
j
.
• V
j
indicates the jth partition of a feature P
i
. This
implies that the value for V
j
chosen by an SMT
solver determines which particular partition is se-
lected.
• F
i
is a criteria f ormula that is connected with a
partition switch, indicating that when a partition
switch is on the criteria f ormula must be applied.
For different partition-based criteria, ensuring that
the instances generated by the SMT solver achieve
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
42

• When an attribute d is an integer type:
((T
i
= 0) ∧ (d < p)) ∨ ((T
i
= 1) ∧ (d = p))
∨ ((T
i
= 2) ∧ (d > p))
• when an attribute d is a boolean type:
((T
i
= 0) ∧ (d = f alse)) ∨ ((T
i
= 1)
∧(d = true))
Figure 3: SMT encoding for partitioning integer and
boolean type attribute.
those criteria, depends on criteria formulas in each
constraint. These criteria formulas are captured by
the corresponding SMT encoding, and we elaborate
these encodings in the Section 3.1 and 3.2.
3.1 Partitioning for Class Attributes
Achieving CA coverage requires that a constraint cov-
ers every partition created for each attribute, and this
is controlled by criteria formula. In other words, the
criteria formulas determine what value is to be as-
signed for an attribute in each instance.
Our current approach supports two types of at-
tributes: integer and booelan, and the SMT encodings
for those two types of attribute are presented in Figure
3.
As shown in Figure 3, for each ith attribute in a
class, a partition switch (T
i
) is created. For an inte-
ger type attribute, T
i
has a value of 0, 1 or 2 indicat-
ing 3 partitions: > p , = p and < p , where p is a
representative value chosen by a user, each partition
has a corresponding criteria formula. If no particu-
lar value is given, a value p = 0 will be chosen as
default. These three partitions are directly expressed
into SMT formulas. Similarly, an SMT encoding for
a boolean type attribute is formed except that the par-
tition switch is either 0 or 1, since a boolean value can
only be true and f alse.
3.2 Partitioning Associations
Associations between classes are an important part of
a metamodel, and it is desirable that generated in-
stances should also cover these associations for dif-
ferent partitions. The standard coverage criteria for
associations, known as Association-end multiplicity
(AEM), has already been defined in (Andrews et al.,
2003), and in this section we show how this can be
extended to metamodels and incorporated into our ap-
proach.
3.2.1 Partitioning Unidirectional Associations
To implement AEM coverage for unidirectional asso-
ciation, we specify criteria formulas corresponding to
the most frequently used association types defined in
a metamodel based on their multiplicities. These cri-
teria formulas determine how each node (object) in an
instance can be linked to others. For an association,
we form all possible links from typed node to another
based on the bound defined for each class at both as-
sociation ends, and we then apply the corresponding
translation rule to form a set of SMT formulas.
As shown in section 2.2, we use an adjacent matrix
E
re f
to represent all possible links for an association
re f between class A and B. The rows of the matrix,
denoted as E
row
, represent all links from one instance
of A to one instance of B. The columns of the matrix,
denoted as E
col
, represent all links from one instance
of B to one instance of A. Each entry e
i, j
in E
re f
is an
SMT boolean variable.
Figure 4 summarises 4 rules for common unidi-
rectional association patterns. For each rule, there is a
partition switch that is either 0 or 1 indicating that the
association is divided into two partitions. For exam-
ple, the second formula in Figure 4 shows an example
of the translation rules for unidirectional association
pattern 1..∗. This rule states that this association can
be partitioned into two partitions, and each partition is
controlled by a partition switch (T ) and a criteria for-
mula. One partition is that for each instance of A is as-
sociated with exactly one instance of B, and the other
is for each instance of A is linked with a k number
of instances of B. In order to know the exact k num-
ber of instances of B that can be associated with an
instance of A, both criteria formulas (associated with
T ) consist of an auxiliary matrix (Aux), where each
element (Aux
i, j
) in that matrix is an integer SMT vari-
able. Each Aux
i, j
uses either 1 or 0 to denote whether
a link in E
re f
is selected or not. To compute k number
of instances of B that connect to an instance of A, we
add up all Aux
i, j
s in the same row to k. For exam-
ple, Figure 5 shows a possible assignment found by
an SMT solver. Each instance of A is connected to 3
instances of B, since each row in the array is added
up to 3. Once an Aux
i, j
is chosen to be one, the cor-
responding e
i, j
in the matrix E
re f
is also switched on
(set to true). This indicates that a relevant link is pre-
sented in the instance.
3.2.2 Partitioning Bidirectional Associations
A bidirectional association distinguishes a unidirec-
tional association by counting links in two directions.
Therefore, a translation rule for a bidirectional asso-
ciation constrains both E
row
and E
col
. In general, the
translation rules in Figure 6 are similar to unidirec-
tional except that we need to correctly calculate the
possible maximum number of instances of B that an
instance of A connects to.
Generating Metamodel Instances Satisfying Coverage Criteria via SMT Solving
43

Association Pattern
Translation Rule
(Unidirectional)
(1) ((T = 0) ∧
|E
row
|
V
i=1
|E
col
|
W
j=1
¬e
i, j
)
∨ ((T = 1) ∧ (
|E
row
|
V
i=1
(
|E
col
|
W
j=1
(
|E
col
|
V
k=1,k6= j
¬e
i,k
) ∧ e
i, j
)))
(2) ((T = 0) ∧
|E
row
|
V
i=1
(
|E
col
|
∑
j=1
Aux
i, j
) = 1)
∨ ((T = 1) ∧
|E
row
|
V
i=1
(
|E
col
|
∑
j=1
Aux
i, j
) = k ∧ |E
col
| > 1)
where 1 < k ≤ |E
col
|
(3) ((T = 0) ∧
|E
row
|
V
i=1
|E
col
|
W
j=1
¬e
i, j
)
∨ ((T = 1) ∧
|E
row
|
V
i=1
(
|E
col
|
∑
j=1
Aux
i, j
) = k ∧ |E
col
| ≥ 1)
where 1 ≤ k ≤ |E
col
|
Figure 4: Translation rules for unidirectional association patterns.
Aux =
b
1
b
2
b
3
b
4
b
5
a
1
0 1 0 1 1
a
2
1 0 1 0 1
a
3
0 1 1 1 0
Figure 5: An example of a possible assignment found by an
SMT solver for the auxiliary matrix.
For example, the second rule in Figure 6 is for a
bidirectional association pattern 1 ↔ 1..∗
2
. This pat-
tern is partitioned into two partitions. One is for each
instance of A is connected to exactly one instance of
B, and one instance of B can only connect to one in-
stance of A. The other partition allows one instance
of A to connect to multiple instances of B. Both parti-
tions are controlled by a partition switch (T ), and have
two different criteria formulas. The first criteria for-
mula specifies the first partition is one instance of A
connects exactly one instances of B, and one instances
of B can only connect to one instances of A.
Since the second partition allows k number of in-
stances of B to be connected to an instance of A, the
criteria formula needs to compute the maximum pos-
sible number of instances of B that an instance of A
can connect to. We compute this number k by calcu-
lating the difference between the bound of B and the
bound of A, and adding 1. Thus, |E
row
| specifies b(A)
while |E
col
| gives b(B). To understand how k gets cal-
culated, we consider the following three scenarios:
1. |E
col
| = |E
row
|: we have equal number instances
2
We use x ↔ y to denote a bidirectional association with
two multiplicities x and y at two association ends
of A and B. Since the multiplicities for two
association-ends (1 and 1..∗) tell us that one in-
stance of A must be connected to at least one in-
stance of B, and one instance of B can only be
linked to one instance of A, this scenario now im-
plies that each instance of A connects each in-
stance of B, vice versa. Thus, the maximum num-
ber of instances of B that an instance of A can con-
nect to is k = 1.
2. |E
col
| > |E
row
|: we have more instances of B than
A. We first connect every instance of A to one
instance of B, and every instance of B connects
to only one instance of A. Now, we can add the
remaining number instances of B to one of the ex-
isting connections between instance of A and B,
and counts one link as already having been estab-
lished. Thus, k gives the maximum number of Bs
that one of the instance of A can connect to.
3. |E
col
| < |E
row
|: we have less instances of B than
A. However, this scenario violates the constraint
implied by the multiplicities, and is thus ruled out.
In all possible cases the minimum number of in-
stances of B has to be equal to the number instances
of A. Figure 7 shows an example where one instance
of A can connect to at most 3 (here we set k = 3) in-
stances of B.
Similarly, rule 1 in Figure 6 states that when the
first partition is chosen (T is 0), no links encoded by
e
i, j
are chosen. When the second partition is chosen
(T is 1), only one e
i, j
is chosen. This indicates that
a link (e
i, j
) between each instance of A and B is al-
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
44

Association Pattern
Translation Rule
(Bidirectional)
(1) ((T = 0) ∧
|E
row
|
V
i=1
|E
col
|
W
j=1
¬e
i, j
)
∨ ((T = 1) ∧
|E
row
|
W
i=1
(
|E
col
|
∑
j=1
Aux
i, j
) = 1)
(2) ((T = 0) ∧
|E
row
|
W
i=1
(
|E
col
|
∑
j=1
Aux
i, j
) = 1)
∨ ((T = 1) ∧
|E
row
|
W
i=1
(
|E
col
|
∑
j=1
Aux
i, j
) = k) ∧ |E
row
| < |E
col
|
where 1 < k ≤ |E
col
| − |E
row
| + 1
(3) ((T = 0) ∧
|E
row
|
V
i=1
|E
col
|
W
j=1
¬e
i, j
)
∨ ((T = 1) ∧
|E
row
|
W
i=1
(
|E
col
|
∑
j=1
Aux
i, j
) = k) ∧ |E
row
| ≤ |E
col
|
where 1 ≤ k ≤ |E
col
| − |E
row
| + 1
Figure 6: Translation rules for bidirectional association patterns.
Aux =
b
1
b
2
b
3
b
4
b
5
a
1
1 0 0 1 1
a
2
0 0 1 0 0
a
3
0 1 0 0 0
Figure 7: An example of an assignment found by an SMT
solver for an association between two classes A and B,
where the bounds for A and B are 3 and 5, respectively.
In this example an instance of A is linked with a maximum
of 3 instances of B. Since the sum of each column is 1, an
instance of B is only connected to a single instance of A.
lowed to be presented. Rule 3 for the association pat-
tern (1 ↔ ∗) has a criteria formula that combines the
first criteria formula from the first association-pattern
(1 ↔ 0..1) with the second criteria formula from the
second association-pattern (1 ↔ 1..∗) as they indicate
that either no links are chosen at all or choose exactly
k number of links between an instance of A and B.
4 INSTANCE GENERATION
USING GRAPH-BASED
CONSTRAINTS
The techniques described in the previous sections al-
low coverage criteria to be achieved for the class at-
tributes and associations in a metamodel. As such
they are standard coverage criteria for UML class di-
agrams, and may be applied to any metamodel. How-
ever, it is reasonable to suppose that a user will have
more sophisticated requirements, and wish to direct
the generation of instances so as to satisfy other con-
straints. For this reason, we present a new technique
that allows instance generation to meet the following
graph-based properties.
4.1 Directed Acyclic Graphs
Directed acyclic graphs (DAGs) are commonly used
in many areas, for example, the topology of a net-
work, data flow diagrams, etc. Regarding metamod-
eling, one may require a program to have a particular
depth of inheritance tree, or a particular call depth.
Thus, to ensure the generation of a DAG from a re-
flexive association in a metamodel, we only enable
the elements that are in the upper triangle of the ad-
jacency matrix, and disable the rest of the e
i, j
s in the
matrix, breaking all the cycles in the graph.
4.2 Sharing and Non-sharing Nodes
Since we use an adjacency matrix to capture all pos-
sible links (within the bounds) for an association, we
can also manipulate this matrix to form new formu-
las that can express how links are connected to each
other. In particular, we can facilitate the specifica-
tion of graph-based constraints by the user that will
direct instance generation. In order to facilitate in-
stance generation with such properties, we introduce
the following new properties.
In a graph, some nodes may have all their out-
going edges going to the same node and some may
not. We consider these nodes having sharing and non-
Generating Metamodel Instances Satisfying Coverage Criteria via SMT Solving
45

sharing properties. Sharing and non-sharing proper-
ties can only be applied to a non-reflexive association.
Before we precisely define sharing and non-sharing
properties, we first define two functions ( f and g).
1. Function f is an out-adjacency function (Ad j
+
)
that computes a set of nodes from all out-going
edges of a particular node. f : V
G
→ 2
V
G
, where
V
G
is the set of nodes, and 2
V
G
is the power set of
V
G
.
2. Function g is an in-adjacency function (Ad j
−
) that
computes a set of nodes from all in-coming edges
of a particular node. g : V
G
→ 2
V
G
, where V
G
is the
set of nodes, and 2
V
G
is the power set of V
G
.
With functions f and g, we are able to calculate a
set of nodes based on their in-coming and out-going
edges. Now we can use these two functions to define
the following sharing and non-sharing properties:
• A set of nodes L = {N
1
,N
2
,..., N
j
}, where |L| ≥
2, are said to be strong sharing nodes iff
(
j
T
i=1
f (N
i
)) 6=
/
0, ∀L
x
∈
j
S
i=1
f (N
i
) and g(L
x
) ⊆ L.
• A set of nodes L = {N
1
,N
2
,..., N
j
}, where |L| ≥ 2,
are said to be weak sharing nodes iff (
j
T
i=1
f (N
i
)) 6=
/
0, ∃L
x
∈
j
S
i=1
f (N
i
) and L ⊂ g(L
x
).
• A set of nodes L = {N
1
,N
2
,..., N
j
}, where |L| ≥ 2,
are said to be strong non-sharing nodes iff ∀L
i
∈
L, | f (N
i
)| = 1 and f (N
a
) ∩ f (N
b
) =
/
0, where 1 ≤
a < b ≤ j.
• A set of nodes L = {N
1
,N
2
,..., N
j
}, where |L| ≥ 2,
are said to be weak non-sharing nodes iff ∀N
i
∈ L,
| f (N
i
)| > 1 and f (N
a
)∩ f (N
b
) =
/
0, where 1 ≤ a <
b ≤ j.
To understand these definitions, we use two exam-
ples to illustrate sharing and non-sharing properties.
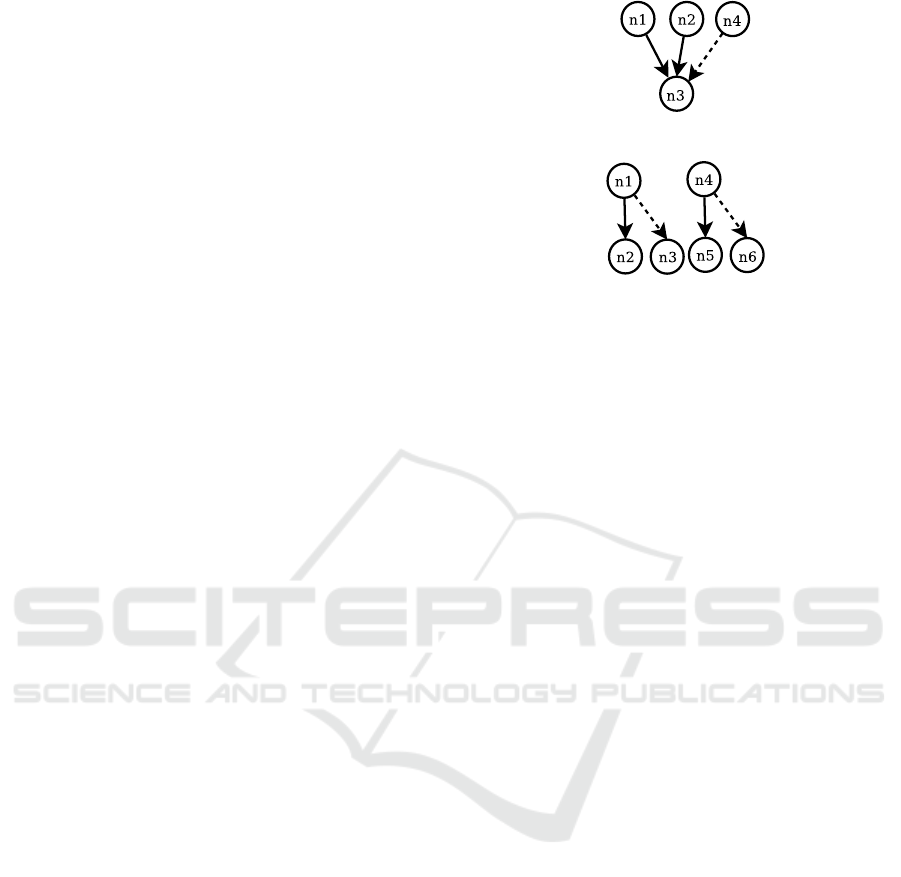
In Figure 8, a solid line is used to denote the exist-
ing links and a dashed line is used to represent pos-
sible links. The set of nodes n1 and n2 (with solid
lines) are considered as strong sharing nodes since
both their out-adjacency functions return n3 ( f (n1) =
f (n2) = {n3}), and n3’s in-adjacency function returns
n1 and n2 (g(n3) = {n1, n2}) . In other words, n3
can only be accessed by both n1 and n2 and no other
nodes. However, if a link from n4 to n3 is connected,
then the set of nodes n1 and n2 are regarded as weak
sharing nodes because n3’s in-adjacency function this
time returns three nodes: g(n3) = {n1,n2,n4}. Thus,
the set of nodes n1, n2 and n4 are considered as
strong sharing nodes ( f (n1) ∩ f (n2) ∩ f (n4) = n3),
and g(n3) ⊆ {n1,n2, n4}).
Figure 8: An example of sharing nodes in a graph.
Figure 9: An example of non-sharing nodes in a graph.
Similarly, in Figure 9 the solid lines between
nodes n1, n2 and n4, n5 make the set of nodes n1 and
n4 strong non-sharing nodes in the graph (| f (n1)| =
| f (n4)| = 1, and f (n1) ∩ f (n4) =
/
0). If n1 also con-
nects to n3 (a possible link), and n4 connects to n6,
then the set of nodes n1 and n2 are weak non-sharing
nodes, since they all connect to more than one other
node (| f (n1)| = | f (n4)| > 1).
Figure 11 shows a matrix for capturing an asso-
ciation in a metamodel. Suppose we want to give
strong sharing property to a set of nodes L = {a
1
,a
4
}.
This indicates that at least one of the b
0
s must be
shared by them. For example, e
1,1
and e
1,4
could be
selected at the same time, or e
2,1
and e
2,4
are cho-
sen ((e
1,1
∧ e
1,4
) ∨ (e
2,1
∧ e
2,4
)). This represents that
a
1
and a
4
they both have out-going edges to b
1
or
b
2
. This is captured by the first sub-formula of rule
(2) from Figure 10. Now, suppose e
1,1
and e
1,4
are
selected, then anything between them cannot be se-
lected otherwise they are not strong sharing nodes.
Thus, e
1,2
and e
1,3
are disabled when e
1,1
and e
1,4
are selected ((e
1,1
∧ e
1,4
) → (¬e
1,2
∧ ¬e
1,3
)). This is
captured by the second sub-formula of rule (2) from
Figure 10.
Similarly weak sharing, strong and weak non-
sharing properties are captured in rule (1) (3) and (4)
in Figure 10. In each formula listed in Figure 10, we
use L to denote a set of nodes to be assigned with one
of the four properties, and |L| ≥ 2. For weak shar-
ing property, the Formula is similar to the Formula
for strong sharing property except that we drop the
second sub-formula. Instead, we add a formula that
states that at least one of the a
0
s not specified in L can
be linked to the b
0
s. The formula for the strong non-
sharing property indicates that only one link can be
selected according to specified nodes in L. It indicates
that as long as one link is selected all other links in the
same row and column are switched off. Similarly, for
weak non-sharing property, the formula indicates that
there could be multiple links selected according to a
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
46

Property SMT Formula
(1) Weak sharing
|E
row
|
W
i=1
|L|
V
k=1
e
i,L
k
∧
|E
row
|
V
i=1
|E
col
|
W
j=1, j /∈L
e
i, j
(2) Strong sharing (
|E
row
|
W
i=1
|L|
V
k=1
e
i,L
k
) ∧ (
|E
row
|
V
i=1
(
|L|
V
k=1
e
i,L
k
→
|E
col
|
V
j=1, j /∈L
¬e
i, j
))
(3) Strong non-sharing
(
|L|
V
k=1
|E
row
|
W
i=1
(
|E
row
|
V
j=1, j6=i
¬e
j,k
) ∧ e
i,L
k
) ∧ (
|E
row
|
V
i=1
(
|L|
V
k=1
e
i,L
k
→
|E
col
|
V
j=1, j /∈L
¬e
i, j
))
(4) Weak non-sharing (
|L|
V
k=1
|E
row
|
W
i=1
e
i,L
k
) ∧ (
|E
row
|
V
i=1
(
|L|
V
k=1
e
i,L
k
→
|E
col
|
V
j=1, j /∈L
¬e
i, j
))
Figure 10: The SMT formulas for capturing sharing/non-sharing properties.
a
1
a
2
a
3
a
4
b
1
e
1,1
e
1,2
e
1,3
e
1,4
b
2
e
2,1
e
2,2
e
2,3
e
2,4
b
3
e
3,1
e
3,2
e
3,3
e
3,4
Figure 11: An example of matrix for illustrating sharing
and non-sharing properties. In this example, each e
i, j
is
represented as a link from a
j
to b
i
.
specific node in L. This indicates that a node can con-
nect to at least one or more nodes. Since connections
to multiple nodes are allowed, all other nodes in the
same row must be disabled.
5 EVALUATION
In this section, we first briefly describe a tool that
is extended with partition-based and graph-based in-
stance generation, then we present our initial evalua-
tion, and finally we discuss its capabilities and limita-
tions.
5.1 Implementation
We have implemented and integrated the partition-
based and graph-based criteria described in this pa-
per in our existing tool, ASMIG
3
. ASMIG takes in
a metamodel in ecore format (with a bound defined
for each class in that metamodel) and an OCL file,
outputs all consistent models (if it has any) within
those bounds. To enumerate “all possible” instances,
ASMIG blocks all previously generated instances by
adding the negation of satisfiable assignments found
by an SMT solver one at a time until no more satisfi-
able assignment is possible. ASMIG is purely written
in Java and it consists of about 22000 (excluding UI)
lines of code (LOC) with about 8300 LOC dedicated
to the techniques described in this paper. To construct
ASMIG, we re-engineered a parser extracted from the
3
available at: https://bitbucket.org/classciwuhao/asmig
USE tool (Kuhlmann et al., 2011), adapting it to use
as our front-end for reading the OCL invariants. The
current version of ASMIG uses Z3 as its default back-
end SMT solver (De Moura and Bjørner, 2008), sup-
ports generating formulas in SMT2 standard (Barrett
et al., 2010).
5.2 Results
The evaluation for both partition-based and graph-
based criteria is performed on a machine with a
2.93GHz Intel Core 2 Duo and 4GB memory, the
results and time are recorded in Figure 12 and 13.
More detailed results, along with further examples,
are available at our website
8
.
Figure 12 shows the results for partition-based cri-
teria based on a total of 15 metamodels. For each
metamodel, we record translation time and average
instance generation time. To evaluate scalability, we
select a variety of metamodels such as general pur-
pose programming languages, domain specific lan-
guages, ranging from small size to large size. We
believe these metamodels are good representatives in
terms of their usage in different domains. To effec-
tively evaluate partition-based technique, we change
ASMIG’s internal configuration in order to set a large
enough upper bound for each non-abstract class, this
would guarantee each non-abstract class to be ini-
tialised at least once and up to that upper bound. The
total bounds column in Figure 12 shows the sum of
each bound for every non-abstract class in the meta-
model. The total instances column indicates the num-
ber of instances generated in order to achieve full cov-
erage for the CA and AEM criteria. For the class at-
tributes coverage criteria (CA), ASMIG allows users
4
Available at: http://www.emn.fr/z-info/atlanmod/
5
From Eclipse Modeling Framework Royal and Loyal
Example Project
6
Extracted from Eclipse Modeling Framework
7
Available at: http://www.jamopp.org/
8
http://www.cs.nuim.ie/∼haowu/ASMIG/Results/
Generating Metamodel Instances Satisfying Coverage Criteria via SMT Solving
47

Number of Total Time in ms
Metamodel Classes Assocs Attribs Bounds Instances Translation Avg Finding
Finite State Ma-
chine 1.0
4
16 7 0 16 4 485 30
DOT (Graphviz)
1.0
4
26 20 0 21 4 512 50
Royal & Loyal
5
15 41 2 40 8 535 65
Ant
4
48 27 0 56 4 673 71
CPL 1.0
4
32 16 0 38 4 513 91
Maven
(maven.xml)
0.3
4
58 32 0 65 4 559 108
Ecore
6
22 40 0 31 4 585 195
UML2 Class Dia-
gram
6
40 26 46 35 8 721 966
HTML
4
59 7 0 59 4 673 1562
Java
7
233 104 1 183 8 971 2629
Company
8
7 6 6 13 12 487 36
C++ 1.0
4
16 4 5 20 8 499 22
GraphML
4
11 13 2 20 8 496 53
Hierarchical State
Machine 1.0
4
15 16 0 33 4 510 72
BibTexML1.2
4
28 4 0 18 4 510 28
Figure 12: Results of using our tool to generate instances of 15 publicly-available metamodels. For each metamodel we show
its size (in terms of classes, associations and attributes), the bound on the number of classes in a metamodel, the number of
instances generated, and two measures of the time taken.
to choose a representative value, but for general pur-
pose, we choose the default value 0 to obtain three
partitions (< 0, = 0 and > 0) for each integer type
attribute. For the association-end multiplicity criteria
(AEM), we set 3 instances as an upper bound for each
association that has a multiplicity of ∗. We choose
this upper bound because it is easy for us to distin-
guish this from a one-to-one multiplicity for both as-
sociation ends.
Figure 13 shows the results for ASMIG to gen-
erate 100 instances of a subset of Java program-
ming language metamodel based on specific bounds
for four different CK metrics (Chidamber and Ke-
merer, 1994). We choose this metamodel because
the graph-based criteria focus on a specific associ-
ation such as an inheritance relationship must be a
directed acyclic graph. We choose CK metrics be-
cause these metrics possess good graph properties.
For simplicity, we consider the complexity of WMC
as the sum of the methods in a class. To correctly
calculate LCOM value, we first use an SMT solver
to select a list of nodes to be connected, then apply
sharing/non-sharing properties to those nodes. There
are a number of possible definitions of the LCOM
metric which are supported by ASMIG. We choose
LCOM3 here which represents the methods accessing
common fields as a connected graph. Thus, a value of
2 for LCOM3 means 2 connected graphs with respect
to method accessing fields. For each of the four met-
rics in Figure 13 we specified three different metric
values (shown in the values column) causing the cal-
culated bounds to vary between 3 to 10. For DIT, we
directly apply the method described in Section 4.1.
For NOC, we first fix the number of links between
two nodes via an auxiliary matrix as shown in Sec-
tion 3.2, then apply strong sharing properties to these
nodes. All the detailed instances generated for above
metrics are available at our website
8
.
5.3 Discussion
Capabilities. (1) The partition-based technique in
section 3.1 and section 3.2 allows one to achieve a
full equivalence partitioning testing by iteratively se-
lecting a different representative value. Equivalence
partitioning testing is considered as one of the im-
portant techniques for testing object oriented system
(Binder, 1999) (Gutjahr, 1999). For CA, equivalence
partitioning testing for a valid range of 0..100 can be
achieved via two steps. Firstly, pick 0 as the rep-
resentative value covering < 0, = 0 and > 0, then
choose 100 covering < 100, = 100 and > 100. Sim-
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
48

CK Metric Total Time in ms
Metric Value Bound Translate Finding
WMC
2 3 446 31
3 6 444 59
5 10 461 120
DIT
2 3 456 53
4 6 457 54
8 10 460 180
NOC
2 3 469 64
4 6 481 65
8 10 489 180
LCOM
2 3 476 63
2 6 470 42
3 10 484 138
Figure 13: Results of generating 100 instances which sat-
isfy constraints based on four of the CK metrics. Each met-
ric was constrained using three values, and the calculated
bounds are shown, as well as two measures of the time taken
to generate appropriate instances.
ilarly, for AEM, one can set a larger bound just out-
side the boundary (the boundary can be decided by
using knowledge of the problem domain) for each
class at two ends of an association. (2) Having in-
stances meeting graph-based constraints provides a
way of analysing or measuring a software system
such as generating a control flow graph via specify-
ing sharing/non-sharing properties on specific nodes.
Viewing a metamodel or an instance as a graph brings
one kind of diversity of instance generation for those
who require models that are based on particular shape
of a graph.
Limitations. (1) Currently, our SMT formulas do
not fully support a graph criteria that constrains over
more than a single association. For example, metrics
like response for a class (RFC) or coupling between
object classes (CBO) typically constrain over two dif-
ferent associations. However, this can be avoided via
a sequence of SMT solving, and use the assignment
from previous successful solving as the input to the
next SMT solving. For example, for RFC, one could
fix a set of methods first, then use SMT solver to
distribute the number of methods directly called by
that set of methods, finally apply sharing/non-sharing
properties to those methods are selected from previ-
ous SMT solving. (2) We admit that both partition-
based and graph-based criteria may not be sufficient
enough to fulfill users’ expectation of the diversity of
instances. One may certainly require a different crite-
ria for validating a metamodel based on different test-
ing strategies. CA and AEM criteria both are part of
standard coverage criteria for UML class diagrams,
and graph-based criteria provides a way of generating
instances based on describing graph properties. With
both kinds of instance generation, we can at least pro-
vide a certain degree of confidence in designing, test-
ing or validating a metamodel. In the future, we will
investigate a more general approach that would allow
language engineers to describe customised coverage
criteria via a simple domain specific language.
6 RELATED WORK
One of the challenges with metamodelling is that it
is difficult to instantiate a metamodel since instances
have to conform to both the metamodels’ structural
constraints and additional semantic constraints writ-
ten in a language such as OCL. Although much recent
research has endeavoured to instantiate metamod-
els using different approaches and techniques (Anas-
tasakis et al., 2007; Ehrig et al., 2009; Gonz
´
alez P
´
erez
et al., 2012; Macedo and Cunha, 2013), the ability to
coverage criteria directed instance generation is still
quite limited.
One of the earliest approaches to generating pro-
grams using coverage criteria is Purdom’s algorithm,
based on generating programs that cover all the rules
in a context free grammar (CFG) (Purdom, 1972).
However, a metamodel captures more than a CFG be-
cause the static semantics can be defined, e.g. using
extra OCL constraints. Though work has been done
on extending Purdom’s approach to attribute gram-
mars (Harm and L
¨
ammel, 2000), thus incorporating
semantic constraints, the core generation framework
is still based on rule coverage, and more general cov-
erage criteria are not considered.
The most closely related research to our work is
the model finding tool Alloy (Jackson, 2002). Alloy
translates a relational specification into formulas for
a SAT solver, and each successful assignment for the
SAT instances can be mapped back to the problem
domain, and much of the research built around Al-
loy facilitates instance generation. In previous work
we have used Alloy to generate instances of meta-
models using the Eclipse Modeling Framework, and
then applied test-suite reduction techniques in order to
pick out instances contributing to a coverage criteria
(McQuillan and Power, 2008). However much of our
work (and that of others) was limited by the capabil-
ities of Alloy, particularly in relation to coverage ori-
ented generation and quantitative constraints (Anas-
tasakis et al., 2007; Bordbar and Anastasakis, 2005;
Kuhlmann et al., 2011; Sen et al., 2009; Kuhlmann
and Gogolla, 2012).
The latest version of Alloy employs a powerful
relational engine called kodkod (Torlak and Jackson,
2007), which outperforms previous versions of Alloy
Generating Metamodel Instances Satisfying Coverage Criteria via SMT Solving
49

on large-scale problem solving. However, a major
disadvantage is the dependence on SAT solvers which
perform poorly when dealing with numeric quanti-
ties, using calculations such as addition, multiplica-
tion, comparison, etc.
Graph grammars offer a natural way to describe
the instance generation process and so have an advan-
tage for generating metamodel instances (Ehrig et al.,
2009; Hoffmann and Minas, 2011). Though graph
grammars deal with graphs, it is more difficult to user
their grammars to quantify a set of nodes than using
first-order logic. Parsing a graph is expensive because
graph matching is not always deterministic. Thus, the
cost of using graph grammars to produce instances
that meet graph-based constraint could be very high.
Cabot et al. propose a detailed systematic pro-
cedure that reduces the problem of UML class di-
gram instantiation to a Constraint Satisfaction Prob-
lem (CSP) (Gonz
´
alez P
´
erez et al., 2012; Cabot et al.,
2008; Cabot et al., 2014). The main advantage is that
CSP provides a high-level language so that a partic-
ular constraint problem is programmable. Our ap-
proach distinguishes with theirs by reducing it to an
SMT problem. SMT encoding provides a much better
expressiveness power than SAT, and it is more natu-
ral to encode a problem into SMT formulas. Much
research has been made in improving SMT solvers’
expressiveness and performance (Barrett et al., 2010;
De Moura and Bjørner, 2008; Barrett et al., 2011;
Cimatti et al., 2013), which make them more suit-
able for complicated tasks such as verification, test
case generation, program synthesis, etc (B
¨
uttner et al.,
2012; Felbinger and Schwarzl, 2014; Tillmann and
De Halleux, 2008; Gulwani, 2010).
Soeken et al. encode a UML class diagram in a set
of operations on bit-vectors which can be solved by
SMT solvers using bit-vector theory (Soeken et al.,
2010). A successful assignment for each bit-vector
can be interpreted as an instance of the UML class di-
agram. They also propose an approach to encode a
subset of OCL constraints as bit-vectors, and provide
a list of corresponding mappings between OCL col-
lection data types and bit-vector operations (Soeken
et al., 2011). However, their approach does not
support structural constraints on the metamodel, es-
pecially the quantitative constraints for associations.
Furthermore, it is unlikely to use their approach to
generate instances satisfying graph-based constraints
because they do not represent a metamodel as a graph
and provide no tool support.
7 CONCLUSION
In this paper, we have presented a new approach to
improve metamodel instance generation by consider-
ing two kinds of coverage criteria: standard coverage
criteria defined for UML class diagram and graph-
based criteria. Both kinds of criteria are translated
to SMT formulas and solved using an external SMT
solver. We have already implemented and integrated
our techniques into a tool, and results reveal both its
capabilities and limitations. In the future, we plan to
improve expressiveness of graph properties to allow
users to be able to describe more complicated graph
shapes. We will also investigate a way of detecting
the conflicts between coverage criteria and OCL in-
variants defined for a metamodel.
REFERENCES
Anastasakis, K., Bordbar, B., Georg, G., and Ray, I. (2007).
UML2Alloy: A challenging model transformation. In
ACM/IEEE 10th International Conference on Model
Driven Engineering Languages and Systems, pages
436–450, Nashville, TN. Springer.
Andrews, A., France, R., Ghosh, S., and Craig, G. (2003).
Test adequacy criteria for UML design models. Soft-
ware Testing, Verification and Reliability, 13(2):95–
127.
Barrett, C., Conway, C. L., Deters, M., Hadarean, L., Jo-
vanovi
´
c, D., King, T., Reynolds, A., and Tinelli, C.
(2011). CVC4. In The 23rd International Confer-
ence on Computer Aided Verification, pages 171–177.
Springer.
Barrett, C., Stump, A., and Tinelli, C. (2010). The SMT-LIB
Standard: Version 2.0. In 8th International Workshop
on Satisfiability Modulo Theories, Edinburgh, UK. El-
sevier Science.
Binder, R. (1999). Testing Object Oriented Systems: Mod-
els, Patterns and Tools. Addison-Wesley.
Bordbar, B. and Anastasakis, K. (2005). UML2Alloy: A
tool for lightweight modelling of discrete event sys-
tems. In International Conference on Applied Com-
puting, pages 209–216, Algarve, Portugal. IADIS.
B
¨
uttner, F., Egea, M., and Cabot, J. (2012). On verify-
ing ATL transformations using ’off-the-shelf’ SMT
solvers. In 15th International Conference on Model
Driven Engineering Languages and Systems, pages
432–448.
Cabot, J., Claris
´
o, R., and Riera, D. (2008). Verification of
UML/OCL class diagrams using constraint program-
ming. In IEEE International Conference on Software
Testing Verification and Validation Workshop, pages
73–80, Berlin, Germany. IEEE Computer Society.
Cabot, J., Claris
´
o, R., and Riera, D. (2014). On the veri-
fication of UML/OCL class diagrams using constraint
programming. Journal of Systems and Software, 93:1–
23.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
50

Chidamber, S. and Kemerer, C. (1994). A metrics suite for
object oriented design. IEEE Transactions Software
Engineering, 20(6):476–493.
Cimatti, A., Griggio, A., Schaafsma, B. J., and Sebastiani,
R. (2013). The mathSAT5 SMT solver. In The 19th
International Conference on Tools and Algorithms for
the Construction and Analysis of Systems, pages 93–
107, Rome, Italy.
De Moura, L. and Bjørner, N. (2008). Z3: an efficient SMT
solver. In 14th International Conference on Tools and
Algorithms for the Construction and Analysis of Sys-
tems, pages 337–340, Budapest, Hungary. Springer.
Ehrig, K., K
¨
uster, J. M., and Taentzer, G. (2009). Generat-
ing instance models from meta models. Software and
Systems Modeling, 8(4):479–500.
Felbinger, H. and Schwarzl, C. (2014). Suitability anal-
ysis of CSP- and SMT-solvers for test case gener-
ation. In The 6th International Workshop on Con-
straints in Software Testing, Verification, and Analy-
sis, pages 40–49. ACM.
Ghosh, S., France, R., Braganza, C., and Kawane, N.
(2003). Test adequacy assessment for UML design
model testing. In 14th International Symposium on
Software Reliability Engineering, pages 332–343.
Gonz
´
alez P
´
erez, C. A., Buettner, F., Claris
´
o, R., and Cabot,
J. (2012). EMFtoCSP: A tool for the lightweight ver-
ification of EMF models. In Formal Methods in Soft-
ware Engineering: Rigorous and Agile Approaches,
Zurich, Suisse.
Gulwani, S. (2010). Dimensions in program synthesis. In
The 12th International ACM SIGPLAN Symposium on
Principles and Practice of Declarative Programming.
ACM.
Gutjahr, W. J. (1999). Partition testing vs. random testing:
The influence of uncertainty. IEEE Transactions on
Software Engineering, 25(5):661–674.
Harm, J. and L
¨
ammel, R. (2000). Testing attribute gram-
mars. In 3rd Workshop on Attribute Grammars and
their Applications, pages 79–99, Ponte de Lima, Por-
tugal.
Hoffmann, B. and Minas, M. (2011). Generating instance
graphs from class diagrams with adaptive star gram-
mars. In 3rd International Workshop on Graph Com-
putation Models.
Jackson, D. (2002). Alloy: a lightweight object modelling
notation. ACM Transactions on Software Engineering
Methodologies, 11(2):256–290.
Kuhlmann, M. and Gogolla, M. (2012). Strengthening SAT-
based validation of UML/OCL models by represent-
ing collections as relations. In Modelling Foundations
and Applications, volume 7349 of Lecture Notes in
Computer Science, pages 32–48. Springer.
Kuhlmann, M., Hamann, L., and Gogolla, M. (2011). Ex-
tensive validation of OCL models by integrating SAT
solving into USE. In 49th International Conference on
Objects, Models, Components, Patterns, pages 290–
306, Zurich, Switzerland. Springer.
Macedo, N. and Cunha, A. (2013). Implementing QVT-R
bidirectional model transformations using Alloy. In
The 16th International Conference on Fundamental
Approaches to Software Engineering, pages 297–311.
Springer, Rome, Italy.
McQuillan, J. A. and Power, J. F. (2008). A metamodel
for the measurement of object-oriented systems: An
analysis using Alloy. In 1st International Conference
on Software Testing Verification and Validation, pages
288–297, Lillehammer, Norway. IEEE Computer So-
ciety.
Myers, G. J. and Sandler, C. (2004). The Art of Software
Testing. John Wiley & Sons.
Ostrand, T. J. and Balcer, M. J. (1988). The category-
partition method for specifying and generating fuc-
tional tests. Communications of the ACM, 31(6):676–
686.
Purdom, P. (1972). A sentence generator for testing parsers.
BIT Numerical Mathematics, 12(3):366–375.
Sen, S., Baudry, B., and Mottu, J.-M. (2009). Automatic
model generation strategies for model transformation
testing. In 2nd International Conference on Theory
and Practice of Model Transformations, pages 148–
164. Springer.
Soeken, M., Wille, R., and Drechsler, R. (2011). En-
coding OCL data types for SAT-based verification of
UML/OCL models. In 5th International Conference
on Tests and Proofs, pages 152–170, Zurich, Switzer-
land. Springer.
Soeken, M., Wille, R., Kuhlmann, M., Gogolla, M., and
Drechsler, R. (2010). Verifying UML/OCL models
using boolean satisfiability. In Design, Automation
Test in Europe Conference Exhibition, pages 1341–
1344, Dresden, Germany.
Tillmann, N. and De Halleux, J. (2008). Pex: White box
test generation for .NET. In The 2nd International
Conference on Tests and Proofs, pages 134–153.
Torlak, E. and Jackson, D. (2007). Kodkod: a rela-
tional model finder. In 13th International Confer-
ence on Tools and Algorithms for the Construction
and Analysis of Systems, pages 632–647, Braga, Por-
tugal. Springer.
Wu, H., Monahan, R., and Power, J. F. (2013). Exploit-
ing attributed type graphs to generate metamodel in-
stances using an SMT solver. In 7th International
Symposium on Theoretical Aspects of Software Engi-
neering, Birmingham, UK.
Generating Metamodel Instances Satisfying Coverage Criteria via SMT Solving
51