Two-photon Excitation of Hydrogen Atom by Sub-Femtoseconds
Electromagnetic Pulses
V. A. Astapenko and S. V. Sakhno
Department of Radioelectronics and Applied Informatics, Moscow Institute of Physics and Technology,
9 Institutsky lane, Dolgoprudnyi, Russia
Keywords: Ultrashort Pulses, Excitation, Sub-Femtoseconds Electromagnetic Pulses, Corrected Gaussian Pulse.
Abstract: The development of methods of generation of ultrashort pulses (USP) of femto- and attosecond duration
ranges with controlled parameters necessitates the theoretical study of features of their interaction with a
matter. Among such features that do not exist in case of “long” pulses should first of all be the nonlinear
dependence of the photoprocess probability W on the USP duration as well as the dependence on the carrier
phase with respect to the pulse envelope. It should be noted that if the dependence of the probability W on
the phase manifests itself either only for very short pulses, when ωt < 1 (w is carrier frequency of the pulse,
t its duration), or in case of a nonlinear photoprocess, the function W(t) can differ from a linear function in
the limit ωt > 1 too for fields of moderate strength, when the perturbation theory is applicable. The present
work is dedicated to the theoretical analysis of two-photon excitation of hydrogen atom in a discrete energy
spectrum by ultrashort electromagnetic pulses of femto- and subfemtosecond ranges of durations. As
examples, excitation of hydrogen atom from the ground state to excited states with a zero orbital moment is
considered.
1 INTRODUCTION
The development of methods of generation of
ultrashort pulses (USP) of femto- and attosecond
duration ranges with controlled parameters
necessitates the theoretical study of features of their
interaction with a matter. The relevance of such
research is mentioned in many contemporary works,
for example in the paper of Hassan, Wirth, Grguras
(2012) and others.
According to Astapenko, Bagan (2013), among
such features that do not exist in case of “long”
pulses should first of all be the nonlinear
dependence of the photoprocess probability W on
the USP duration () as well as the dependence on
the carrier phase with respect to the pulse envelope
().
Apolonski, Dombi, Paulus et al. (2004) are noted
that if the dependence of the probability W on the
phase  manifests itself either only for very short
pulses, when  < 1 ( is carrier frequency of the
pulse), or in case of a nonlinear photoprocess, the
function W() can differ from a linear function in the
limit  > 1 too for fields of moderate strength,
when the perturbation theory is applicable.
To describe photoprocesses in an USP field,
various theoretical methods were used. Thus in the
work of Matveev, Matrasulov (2012) the sudden
perturbation approximation was used to describe
scattering of attosecond pulses by different quantum
systems: atoms, ions, molecules, and clusters. In the
paper of Krainov, Bordyug (2007), excitation of a
two-level system under the USP action was studied
with the use of solution of the Schrödinger equation,
and photoionization of atoms was calculated both
within the framework of the perturbation theory
(Get, Krainov 2013) and in the Landau-Dykhne
approximation (Rastunkov, Krainov 2007). In the
latter work it was shown in particular that ionization
of an atom by an intense single-cycle cosine pulse is
much more efficient than under the action of a sine
pulse.
In the paper of Astapenko (2010), within the
framework of the perturbation theory the formula
was obtained that describes the total probability of
single-photon absorption of an USP (during all time
of its action) in terms of the spectral cross-section of
photoabsorption and the Fourier transform of the
strength of the electric field in a pulse. The
Astapenko, V. and Sakhno, S.
Two-photon Excitation of Hydrogen Atom by Sub-Femtoseconds Electromagnetic Pulses.
DOI: 10.5220/0005650300510054
In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 53-56
ISBN: 978-989-758-174-8
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
53

expression derived in this work was widely used
further (Astapenko 2011) for analysis of single-
photon absorption and spontaneous scattering by
various targets (Rosmej, Astapenko & Lisitsa 2014).
The present work is dedicated to the theoretical
analysis of two-photon excitation of hydrogen atom
in a discrete energy spectrum by ultrashort
electromagnetic pulses of femto- and
subfemtosecond ranges of durations. As examples,
excitation of hydrogen atom from the ground state to
excited states with a zero orbital moment is
considered.
2 CALCULATIONS
The amplitude of the two-photon transition
fi 
during the action of an electromagnetic pulse in the
second order of the perturbation theory is given by
the following expression:

 












 itVtVftdtd
i
A
t
ph
fi
ˆˆ
2
2

(1),
where
  
tEtdtV
ˆ
ˆ

(2),
is the operator of electromagnetic interaction in the
form of a length,

td
ˆ
is the operator of the electric
dipole moment of an atom in the interaction
representation:





 tHidtHitd
00
ˆ
exp
ˆ
ˆ
exp
ˆ

(3),
0
ˆ
H
is the Hamiltonian of an unperturbed atom,

tE
is the electric field strength. We assume an
electromagnetic pulse to be linearly polarized and
the usability condition for the dipole approximation
to be fulfilled.
Using the expansion in terms of the complete system
of functions
n
, from the formulas (1) - (3) we
find:


  
tEtEddtititdtd
i
A
nifn
n
nifn
t
ph
fi
















 exp
2
2

(4),
where
nifn
dd ,
are the matrix elements of the
electric dipole moment of an atom. Now let us
express the electric field strengths in the right-hand
side of the equation (4) in terms of their Fourier
transforms



E
and




E
:
    
;2exp








 dtiEtE
    








 2exp dtiEtE
(5)
and make the substitution of the time variable:






tt
(6),
which will allow integration with respect to the time
t

with appearance of the delta function










fi
(7),
under the sign of integration with respect to the
frequencies





,
. In the formula (7),
fi

is the
transition eigenfrequency that is assumed to be a
positive value.
The formula (7) describes the law of
conservation of energy in excitation of the transition
fi 
by monochromatic components of the
electric field of a pulse




E
and



E
:








fi
(8).
The delta function (7) and accordingly the
equation (8) were obtained under the assumption
that the spectrum of an electromagnetic pulse is
considerably wider than the spectral width of the
transition
fi 
. This assumption is knowingly
fulfilled for neutral atoms and femtosecond (and
shorter) electromagnetic pulses.
It should be noted that if both frequencies





,
are positive, excitation of the transition
occurs due to two-photon absorption, but if one of
these frequencies is negative, there is stimulated
Raman scattering. The negativeness of both
frequencies is impossible since under the assumption
0
fi

, and the equation (8) should be fulfilled.
The presence of the delta function (7) allows
integration with respect to the frequency



, so
under the integral with respect to


d
the product
of electric field strengths will remain:










fi
EE
.
Assuming that the energies of intermediate states
n
have negative imaginary additives, it is possible
to integrate with respect to the time variable

. As a
result, for the probability of two-photon excitation of
the bound-bound transition
fi 
during the
PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology
54

action of a linearly polarized electromagnetic pulse (
z//E
) we obtain the expression:
 





2
2
2
2
22
2
1









fifi
ph
fi
ph
fi
MEEdAW

(9),
here








n
ni
z
ni
z
fn
fi
i
dd
M
0
1
2



(10),
is the two-photon matrix element that for the
transition between states with a zero orbital moment
can be expressed in terms of the radial Green’s
function



irIrrgrfM
plfi





 ;,
3
2
1
2
(11),
where
p
I
is the atomic ionization potential. In
writing the equation (11), the selection rules are
taken into account, from which it follows that in the
case under consideration (
0
fi
ll
) the
contribution to the sum over intermediate states is
made only by states with the quantum number of an
orbital moment
1
n
l
.
It should be noted that the expression (9) is
meaningful in case of applicability of the
perturbation theory, that is, when

1
2

ph
fi
W
.
In calculation of the probability of excitation of a
hydrogen atom we will use the Sturmian expansion
of the Coulomb Green’s function that looks like (in
at. u.):

  




















0
3
1
2!
/2,4,/2,4,4
exp
9
4
;,
k
l
kk
rkFrkFkrrrr
rrg



(12),
where



2
1

(13),

xbaF ,,
is the confluent hypergeometric
function,

z
is the gamma function.
Hereafter we will consider two-photon excitation
of hydrogen atom under the action of a pulse of a
corrected Gaussian shape (CGP). The CGP Fourier
transform is (Rosmej, Astapenko & Lisitsa 2014):

 


22
22
22
0
2
2
2
2
12
,,,













ii
cor
eeEiE
(14),
where
0
E
,

,

are the amplitude, duration,
and carrier frequency of a pulse,


is the “current”
frequency,  is the carrier phase with respect to the
envelope. From the formula (14) it follows in
particular that the constant component of a CGP is
equal to zero:


00
'
 
cor
E
.
Let us introduce the normalized probability of
two-photon excitation:



2
0
2
2
~
E
W
W
ph
fi
ph
fi

(15),
where the amplitude of the electric field strength
0
E
is measured in atomic units.
3 RESULTS
The results of calculations by the above formulas of
the normalized probability of two-photon excitation
of the transition
ss 21 
in a hydrogen atom
under the action of a CGP are given in Figs. 1, 2.
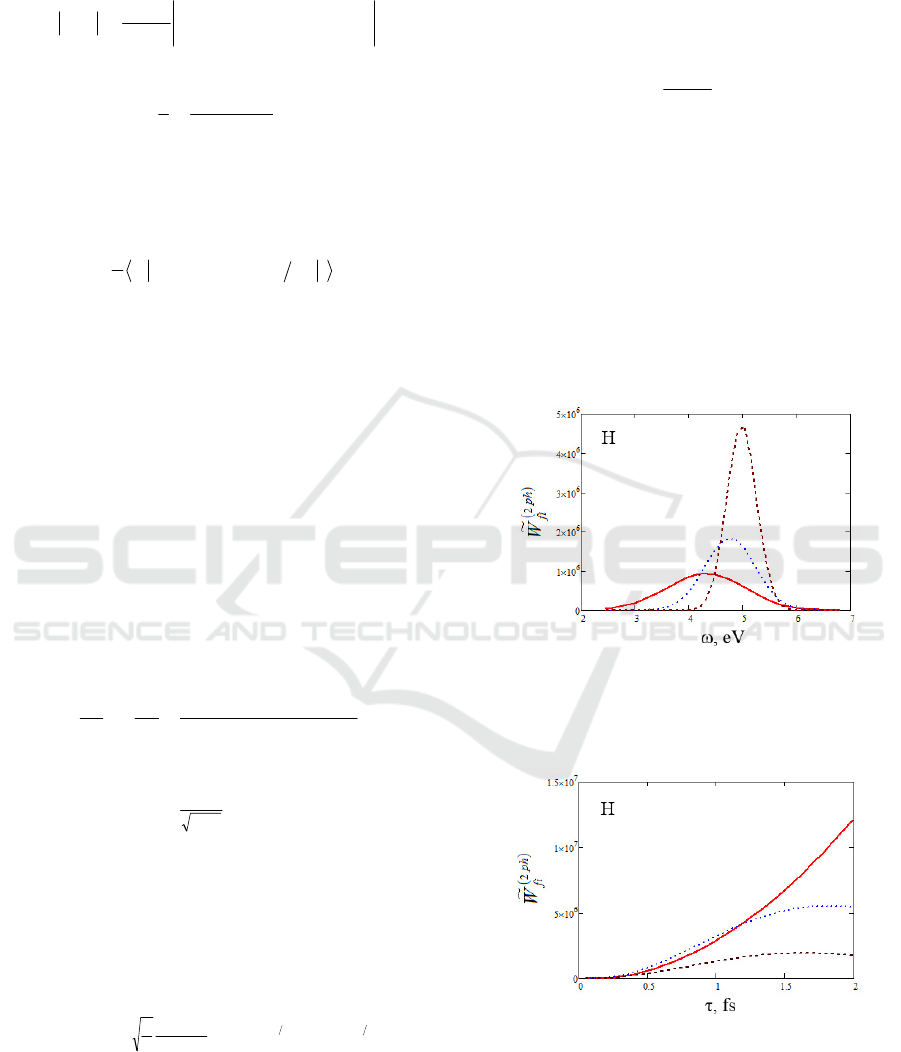
Figure 1: The spectrum of the normalized probability of
two-photon excitation of a hydrogen atom at the transition
1s-2s for different CGP durations: solid curve -  = 0.48
fs, dotted curve -  = 0.72 fs, dashed curve -  = 1.2 fs.
Figure 2: The normalized probability of two-photon
excitation of a hydrogen atom at the transition 1s-2s as a
function of pulse duration for different carrier frequencies
of a CGP: solid curve –  = 5.1 eV (two-photon
resonance), dotted curve -  = 4.84 eV, dashed curve - 
= 5.39 eV.
It should be noted that for E
0
= 10
-2
at. u. the
Two-photon Excitation of Hydrogen Atom by Sub-Femtoseconds Electromagnetic Pulses
55

representative absolute value of the probability of
two-photon excitation of a hydrogen atom for the
problem parameters presented in Figs. 1-2 is 10
-5
.
From Figs. 1-2 it follows that the spectral and time
dependences of the probability of two-photon
excitation of atoms under consideration by femto-
and subfemtosecond pulses are similar and differ
only by numerical values.
Thus in both cases the spectrum of the excitation
probability is broadened with decreasing pulse
duration, and the spectral maximum in this case is
shifted to the region of lower carrier frequencies.
The dependence of the probability of two-photon
excitation on the CGP duration (for
fi


2
) is a
curve with a maximum, the position of which is
shifted to the region of long durations when the
carrier frequency approaches the half transition
frequency. In case of fulfilment of the two-photon
resonance condition
fi


2
, the excitation
probability monotonically increases with pulse
duration.
4 CONCLUSIONS
In the present work, the features of two-photon
excitation of atoms in a discrete spectrum under the
action of ultrashort electromagnetic pulses were
studied theoretically. An expression for the
probability of two-photon excitation of a bound-
bound transition during the action of a linearly
polarized electromagnetic pulse was obtained. Based
on this expression, a case of excitation of hydrogen
atom was considered. A decrease in pulse duration
results in spectral broadening and shift of the
maximum of the spectral dependence to the region
of lower values of carrier frequencies, and a
decrease in the peak value of the probability at the
maximum. In a nonresonance case (
fi


2
), the
probability of two-photon excitation as a function of
pulse duration is a curve with a maximum, the
position of which, with decreasing carrier frequency,
is shifted to the region of long times and is increased
in amplitude. In case of a two-photon resonance
(
fi


2
), the dependence goes to a
monotonically increasing function.
REFERENCES
Apolonski, A., Dombi, P. & Paulus, G., Phys. Rev. Lett.
92 (2004) 073902.
Astapenko, V., Phys. Lett. A. 374 (2010) 1585.
Astapenko, V., JETP. 112 (2011) 193.
Astapenko, V. & Bagan, V., J. Phys. Science and
Application. 3 (2013) 269.
Bordyug, N. & Krainov, V., Las. Phys. Lett. 4 (2007) 418.
Get, A. & Krainov, V., Contrib. Plasma Phys. 53 (2013)
140.
Hassan, M., Wirth, A., Grguras, I., Moulet, A., Luu, T.,
Gagnon, J., Pervak, V. & Goulielmakis, E., Rev. Sci.
Instrum. 83 (2012) 111301.
Matveev, V. & Matrasulov, D., JETP Lett. 96 (2012) 700.
Rastunkov, V. & Krainov, V., J. Phys. B. 40 (2007) 2277.
Rosmej, F, Astapenko, V & Lisitsa, V, Phys. Rev. A. 90
(2014) 043421.
PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology
56