A Practical-time Attack on Reduced-round MISTY1

Nobuyuki Sugio

, Yasutaka Igarashi

, Toshinobu Kaneko

and Kenichi Higuchi

NTT DOCOMO, INC., 3-6 Hikarinooka, Yokosuka, Kanagawa, 239-8536, Japan

Tokyo University of Science,2641 Yamazaki, Noda, Chiba, 278-8510, Japan

Keywords:

MISTY1, Symmetric Key Algorithm, Block Cipher, Higher Order Differential Attack.

Abstract:

MISTY1 is a symmetric key algorithm which has been standardized by ISO and that its modiﬁed version is

used in GSM and 3G mobile networks. MISTY1 is a 64-bit block cipher supporting key length of 128 bits. In

this paper, we focused on evaluating the security of MISTY1 against higher order differential attack. We show

6-round MISTY1 with 4 FL layers is attackable with 2

blocks of chosen plaintexts and 2

43.31

times of data

encryption. This is the best practical-time attack on reduced-round MISTY1.

1 INTRODUCTION

MISTY1 is one of the symmetric key algorithms.

MISTY1 is a 64-bit block cipher supporting key

length of 128 bits. MISTY1 was proposed by Mat-

sui in 1997 (Matsui, 1997). The number of rounds is

8. MISTY1 achieves a provable security against dif-

ferential cryptanalysis and linear cryptanalysis with

round function FO. Designer adds on an auxiliary

function FL in order to become secure against other

attacks. MISTY1 was selected as one of the NESSIE-

recommended ciphers portfolio and was adopted as

the international standard by ISO/IEC 18033-3 (ISO,

2010). CRYPTREC project has chosen MISTY1 as

one of the e-Government Recommended candidate ci-

phers in 2013 (CRYPTREC, 2013). Furthermore, the

block cipher KASUMI designed as a slight modiﬁca-

tion of MISTY1 is used in the GSM/3G mobile net-

works, which makes it one of the most widely used

block ciphers today.

Up to now, many cryptanalytic methods were used

to evaluate the security of MISTY1 such as higher or-

der differential attack, impossible differential attack,

integral attack, and multi-dimensional zero correla-

tion linear attack. The main previous attacks are as

follows. Tsunoo et. al. proposed 46-th order differ-

ential and showed 7-round MISTY1 with 4 FL lay-

ers was attackable with 2

54.1

chosen plaintexts and

120.7

encryptions (Y. Tsunoo and Kawabata, 2008).

Jia et. al. constructed a 7-round impossible differ-

ential and mounted impossible differential attack on

7-round MISTY1 with 3 FL layers (Jia and Li, 2012).

Yi presented zero-correlation linear attack on 7-round

MISTY1 with 4 FL layers, that requires 2

62.9

known

plaintexts and 2

118

encryptions (Yi and Chen, 2014).

Todo introduced Integral attack by division property,

and showed that the secret key of the full MISTY1 can

be recovered with 2

63.58

chosen plaintexts and 2

121

time complexity (Todo, 2015). Bar On improved the

attack proposed by Todo, and presented full MISTY1

was attackable with 2

chosen plaintexts and 2

69.5

encryptions (Bar-On, 2015a).

Most of the previous attacks aimed at maximiz-

ing the number of attacked rounds, and as a result,

their complexities are highly impractical. In this pa-

per, we focused on evaluating the security of MISTY1

in terms of practical-time complexity. The previous

practical-time attack was proposed by Hatano et. al.

(Y. Hatano and Kaneko, 2004), and Dunkelman et. al.

(Dunkelman and Keller, 2013), respectively. The best

practical-time attack was higher order differential at-

tack on 5-round MISTY1 with 4 FL layers.The neces-

sary computational complexity by using higher order

differential can be estimated as sum of the following

2-steps.

1. Preparation of data

2. Key recovery

The order of differential affects both steps. Therefore,

it is very important to discover the lower order differ-

ential characteristics to reduce the complexity for an

attack. The results we obtain are the following.

1. We implemented the 46th-order differential for

4-round MISTY1 introduced in (Y. Tsunoo and

Kawabata, 2008) on a computer which mounted

Graphics Processing Unit (GPU) co-processors

Sugio, N., Igarashi, Y., Kaneko, T. and Higuchi, K.

A Practical-time Attack on Reduced-round MISTY1.

DOI: 10.5220/0005652202350242

In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), pages 235-242

ISBN: 978-989-758-167-0

235

Table 1: Summary of single-key attacks on MISTY1.

Rounds FL layers Data Time Attack algorithm Reference

5 4 2

CP 2

Higher Order Differential (Y. Hatano and Kaneko, 2004)

6 4 2

CP 2

123.4

Impossible Differential (Dunkelman and Keller, 2008)

6 4 2

53.7

CP 2

53.7

Higher Order Differential (Y. Tsunoo and Kawabata, 2008)

6 4 2

CP 2

43.31

Higher Order Differential Section5

7 0 2

50.2

KP 2

114.1

Impossible Differential (Dunkelman and Keller, 2008)

7 3 2

KP 2

124.4

Impossible Differential (Jia and Li, 2012)

7 4 2

62.9

KP 2

118

Multi-Zero Correlation (Yi and Chen, 2014)

7 4 2

54.1

CP 2

120.7

Higher Order Differential (Y. Tsunoo and Kawabata, 2008)

7 5 2

51.45

CP 2

121

Higher Order Differential (Bar-On, 2015b)

8 5 2

63.58

CP 2

121

Integral by division property (Todo, 2015)

8 5 2

CP 2

69.5

Integral by division property (Bar-On, 2015a)

CP: Chosen Plaintexts, KP : Known Plaintexts.

Table 2: The Key Scheduling of MISTY1.

i+2

i+7

i+4

i+5

i+1

i+3

i+1

(odd i) K

i+1

(odd i)

(even i) K

(even i)

and found 16-bits of the above characteristic was

always 0. We gradually reduced the order of dif-

ferentials for 4-round MISTY1 by computer ex-

periment, and discovered new 38-th order differ-

ential characteristics for 4-round MISTY1 which

held 7-bits of those differential characteristics 0

2. We can attack 6-round MISTY1 with 4 FL layers

by using the 38-th order differential characteris-

tic. The complexity for the attack needs 2

cho-

sen plaintexts and 2

43.31

encryptions. Our method

can reduce the necessary number of chosen plain-

texts and the computational cost for the attack of

6-round MISTY1 with 4 FL layers illustrated in

(Y. Tsunoo and Kawabata, 2008) by a factor of

. This is the best practical-time attack on 6-

round MISTY1. Summary of main attacks on

MISTY1 are shown in Table 1.

The remainder of this paper is organized as fol-

lows. Section 2 gives a brief introduction of MISTY1.

Section 3 explains higher order differentials and its

application for an attack. Section 4 shows previous

higher order differentials and presents a new higher

order differential for 4-round MISTY1. Section 5

proposes higher order differential attack on 6-round

MISTY1 with 4 FL layers. Section 6 summarizes this

paper.

The characteristic of 38-th order differential equals to

the characteristic of 46-th order differential for 4-round

MISTY1 estimated in (Y. Tsunoo and Kawabata, 2008)

2 MISTY1

MISTY1 is a Feistel type 64-bit block cipher support-

ing secret key length of 128 bits. MISTY1 was pro-

posed by Matsui in 1997 (Matsui, 1997). The number

of rounds which designer recommends is 8. MISTY1

achieves a provable security against differential crypt-

analysis and linear cryptanalysis with round function

FO. Designer adds on an auxiliary function FL in or-

der to become secure against other attacks.

Figure 1 shows the main structure and components

of the cipher. The round function FO

(1 ≤ i ≤ 8) is

a variant of a 3-round Feistel construction which has

16-bit bijective function FI

i j

(1 ≤ j ≤ 3) and 16-bit

extended key KO

i j

(1 ≤ j ≤ 4), KI

i j

(1 ≤ j ≤ 3). FI

i j

is a variant of a 3-round Feistel construction and its in-

put is divided into left 9-bit data and right 7-bit data,

which are transformed by bitwise XOR operations de-

noted by the symbol ⊕ and substitution tables S7 and

S9. KI

i j1

and KI

i j2

are left 7-bit data and right 9-bit

data of KI

i j

, respectively. The key dependent linear

function FL

are composed of bitwise AND operation

denoted by the symbol ∩, OR operation denoted by

the symbol ∪, XOR operations and KL

i j

(1 ≤ j ≤ 2).

The key schedule of MISTY1 takes the 128-bit se-

cret key K to generate extended keys. Let K

(1 ≤ i ≤

8) be the i-th (from left) 16-bit data of the secret key

K, and let KO

(1 ≤ i ≤ 8) be the output of FI

i j

where

the input of FI

i j

is K

and the key KI

i j

is K

i+1

. Also,

identify K

with K

. The correspondence between the

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

236

Figure 1: Outline of MISTY1.

symbols KO

i j

, KI

i j

, KL

i j

and the actual key is shown

in Table 2. Here, K

is the output of FI

i, j

where the

input is K

and the key is K

i+1

2.1 Notations Used in This Paper

We use the following notations for intermediate val-

ues during the MISTY1 encryptions process.

• The plaintext and ciphertext are denoted by P and

C. The left 32-bit value of P is denoted by P

and

the right 32-bit value of P is denoted by P

. The

left 32-bit value of C is denoted by C

and the

right 32-bit value of C is denoted by C

, respec-

tively.

• The input of i-th round (1 ≤ i ≤ 8) are denoted by

. We denote the intermediate value after appli-

A Practical-time Attack on Reduced-round MISTY1

237

cation of FL functions by X

• Let Z be a intermediate variable. Z[k] denotes k-th

bit of Z and Z[k − l] denotes bits from k to l of Z

respectively.

3 HIGHER ORDER

DIFFERENTIAL ATTACK

This section gives an overview of higher order differ-

ential attack.

3.1 Higher Order Differential (Lai,

1994)

Let E(·) be an encryption function as follows.

Y = E(X;K) (1)

where X ∈ GF(2)

, K ∈ GF(2)

, Y ∈ GF(2)

. For a

block cipher, X, K and Y denote plaintext, key and

ciphertext respectively. Let {a

,· ·· ,a

} be a set

of linearly independent vectors in GF(2)

and V

(i)

be a sub-space spanned by these vectors. We deﬁne

∆

(i)

E(X; K) as an i-th order differential of E(X; K)

with respect to X as follows.

∆

(i)

E(X; K) =

A∈V

(i)

E(X ⊕ A; K) (2)

In the following, we abbreviate ∆

(i)

as ∆

(i)

, when

it is clearly understood. In this paper, we use the

following properties of the higher order differential.

Property 1. If the degree of E(X; K) with re-

spect to X equals to d, then

deg

{E(X; K)} = d ⇔



∆

(d+1)

E(X; K) = 0

∆

(d)

E(X; K) = const

(3)

Property 2. Higher order differential has a linear

property on XOR sum. That means d-th order differ-

ential of the sum of each function equals to the sum

of d-th order differential of each function.

∆

(d)

{E(X

) ⊕ E(X

)} =

∆

(d)

E(X

) ⊕ ∆

(d)

E(X

)

(4)

3.2 Attack Equation

Consider an R-round iterative block cipher. Let

R−1

(X) ∈ GF(2)

be a part of the (R − 1)-th round

output and C(X) ∈ GF(2)

be the ciphertext corre-

sponding to the plaintext X ∈ GF(2)

. H

R−1

(X) is

expressed as follows.

R−1

(X) = F

R−1

(·· ·F

((F

(X;K

);K

),· ·· ,K

R−1

)

(5)

where K

∈ GF(2)

be the i-th round key and F(·) be

a function of GF(2)

× GF(2)

→ GF(2)

If the degree of H

R−1

(X) with respect to X is d,

we have the following equation from Property 1.

∆

(d+1)

R−1

(X) = 0 (6)

This equation holds with probability 1.

Let

F(·) be a decoding function that calculates

R−1

(X) from a ciphertext C(X ) ∈ GF(2)

R−1

(X) =

F(C(X); K

) (7)

where K

∈ GF(2)

denotes the R-th round key to de-

code H

R−1

(X) from C(X). From equation (6), (7) and

(2), we can derive following equation.

A∈V

(d+1)

F(C(X ⊕ A); K

) = 0 (8)

We can determine K

by solving (8). In the following,

we refer to equation (8) as an attack equation for key

recovery.

3.3 Algebraic Method

Shimoyama et al. proposed an effective method

of solving equation (8) (T. Shimoyama and Tsujii,

1999). This method, called algebraic method in this

paper, expands equation (8) as boolean polynomials

over GF(2), and linearizes by treating every higher or-

der variables like k

with new independent variables

like k

i j

. In the following, we use the term linearized

attack equation to refer to an attack equation that is

regarded as a linear equation.

Let L be the number of unknowns in the linearized

attack equation (8). Since the equation (8) is derived

by using an m-bit sub-block, we can rewrite equation

(8) as follows.

Ak = b , k =

,. ..,k

,· ·· ) (9)

where A, b, and k are the m ×L coefﬁcient matrix, the

m-dimensional vector, and the L-dimensional vector

over GF(2). k denotes linearized unknowns that are

expressed as monomials of the R-th round key K

We can obtain m linearized attack equations from

one (d + 1)-th order differential because equation (8)

is an m-bit equation. Therefore we need

L/m

sets

of the (d + 1)-th order differential for the unique so-

lution.

Since one set of (d + 1)-th order differential re-

quires 2

d+1

chosen plaintexts, the necessary number

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

238

of plaintexts D for the determination of a key is esti-

mated as

D = 2

d+1





(10)

If we use the same technique shown in (T. Shimoyama

and Tsujii, 1999), equation (9) requires 2

d+1

×(L+1)

times of

F(·) calculations. Since we have to prepare

L/m

sets of (d + 1)-th order differentials to deter-

mine k, the computational cost

is estimated as

T = 2

d+1

× (L + 1) ×





(11)

Hatano et. al. proposed the optimization for al-

gebraic method by analyzing the number of indepen-

dent unknowns l(≤ L) in equation (8) (Y. Hatano

and Kaneko, 2004). If we can analyze the num-

ber of independent unknowns l(≤ L) in equation (8),

the

l/m

× l coefﬁcient matrix A

and the

l/m

dimensional vector b

is sufﬁcient for solving the

linearized attack equation.

4 HIGHER ORDER

DIFFERENTIALS FOR

REDUCED ROUND MISTY1

This section explains the previous results of higher

order differential characteristic of MISTY1 and il-

lustrates new higher order differential characteris-

tics which we discovered. Here, α and β denote

ﬁxed and variable sub-block respectively. For ex-

ample, 64-bit variable Y consisting of a 3-bit vari-

ables a-th, b-th, and c-th bit of sub-block β (0 ≤

a,b, c ≤ 63, a 6= b 6= c) can be denoted as Y =

{

Y [i] ∈ α, Y [ j] ∈ β | i 6= j, j = a,b,c, a 6= b 6= c

}

. A

3-rd order differential of intermediate variable Z[k −l]

by using Y can be denoted as

Y =

{

Y [i] ∈ α, Y [ j] ∈ β | i 6= j, j = a,b,c,a 6=b 6= c

}

∆

(3)

Z[k − l]

(12)

where 0 ≤ i, j,k,l ≤ 63 and V

(3)

is a subspace based

on variable sub-block Y [ j].

4.1 Previous Results

Hatano et. al. proposed 14-th order differential of

3-round MISTY1 with FL functions (Y. Hatano and

This computational cost ignores the complexity of

solving linearized attack equation, because the computa-

tional cost is negligible as long as coefﬁcient matrix size

is small.

Kaneko, 2004).

P = {P[i] ∈ α, P[ j] ∈ β | i 6= j, 0 ≤ j ≤ 6,

16 ≤ j ≤ 22}

∆

(14)

[63 − 57] = 0

(13)

where V

(14)

is the subspace based on variable sub-

block P[22 − 16, 6 − 0].

Tsunoo et. al. proposed 46-th order differential

which was a 1-round extension of the 14-th order

differential to the direction to plaintext. Due to the

Feistel structure of MISTY1, the 3-round 14-th order

differential can be extended to a 4-round 46-th order

differential by taking all the 2

possible values in the

previous round. Thus, the following theorem could

be derived.

Theorem. For four consecutive rounds of MISTY1

with FL functions that starts at 1-st round, the

following equation independently holds under

any ﬁxed value of the key, constant value of the

P[i] (39 ≤ i ≤ 47, 55 ≤ i ≤ 63) and V

(46)

is the

subspace based on variable sub-blockP

, P[ j]

( 32 ≤ j ≤ 38, 48 ≤ j ≤ 54).

P = {P[i] ∈ α, P[ j], P

∈ β | 39 ≤ i ≤ 47,

55 ≤ i ≤ 63, 32 ≤ j ≤ 38, 48 ≤ j ≤ 54}

∆

(46)

[63 − 57] = 0

(14)

4.2 New Higher Order Differentials for

MISTY1

In this subsection, we describe the new higher order

differential characteristics for MISTY1 which were

discovered by computer experiment.

46-th Order Differential Characteristic. We

implemented 46-th order differential described in

equation (14) on a computer which mounts Graphics

Processing Unit (GPU) co-processors and found the

following 46-th order differential characteristic.

∆

(46)

[63 − 48] = 0 (15)

Although we veriﬁed equation (15) with 10 different

keys and ﬁxed sub-blocks, equation (15) always

held. Since the provability of 10 sets 16-bit random

variables incidentally becomes 0 is 2

−160

, we don’t

think equation (15) accidentally holds.

38-th Order Differential Characteristic. We

gradually reduced the order of differentials in

equation (15) and discovered the new higher order

A Practical-time Attack on Reduced-round MISTY1

239

β shown in 32-bit state (α, β, α, β) are 3-bits variables out of

7-bits sub-blocks, respectively.

Figure 2: A new 38th order differential of MISTY1.

differential characteristics as follows.

P = {P[i] ∈ α,P[ j,k],P

∈ β | i 6= j, i 6= k

32 ≤ i ≤ 63, j = k + 16,

k = h

(32 ≤ h

< h

≤ 38)}

∆

(38)

[63 − 57] = 0

(16)

where h

, h

and h

are bit patterns of variable

sub-block. The variations of 38-th order differential

illustrated in equation (16) exist





=35 patterns.

Other Characteristics. We searched for the new

higher order differential characteristics on 3-round, 4-

round and 5-round MISTY1 respectively. The results

are presented in Table 3.

5 38-TH ORDER DIFFERENTIAL

ATTACK ON REDUCED ROUND

MISTY1

In this section we apply 38-th order differential char-

acteristic to attack 6-round MISTY1 with 4 FL layers.

Table 3: The results of higher order differential characteris-

tics on MISTY1.

We abbreviate ∆

(i)

[63 − 57] = 0 (i = 7,14) as X

[63 − 57] = 0

in the table. This abbreviation is same other characteristics. The

symbol ’N/A’ means that we couldn’t ﬁnd a higher order diffe-

rential characteristic which satisﬁed ∆

(i)

[63 − 41] = 0

(1 ≤ i ≤ 31). (*1) is discovered by Hatano (Y. Hatano and

Kaneko, 2004). (*2)is discovered by Tanaka (H. Tanaka and

Kaneko, 1999). (*3)is discovered by Igarashi (Igarashi and

Kaneko, 2008).

Rounds i-th order diff. Output

FL without FL

3 14

(∗1)

(∗2)

[63 − 57] = 0

3 18 10 X

[63 − 48] = 0

3 N/A 26 X

[63 − 41] = 0

3 32 31 X

[63 − 32] = 0

4 38 32

(∗3)

[63 − 57] = 0

4 44 36 X

[63 − 48] = 0

4 50 47 X

[63 − 41] = 0

4 - 48 X

[63 − 32] = 0

5 - ∼53 Unknown

We estimate the complexity for an attack by means of

same procedure described in (Y. Tsunoo and Kawa-

bata, 2008). Using the chosen plaintext denoted in

equation (16), we have the following attack equation

by assuming KL

[15 − 9] = 0x7 f . (See ﬁgure 3.)

A∈V

(38)

{FO

[63 − 32]; KO

,KO

)[31 − 25]⊕

−1

(X ⊕A);KL

)[31 − 25]} = 0,

[63 − 32] = FL

−1

(X ⊕A);KL

,KL

)

where FL

−1

means an inverse function of FL. We di-

vide the attack equation into seven kinds of 1-bit at-

tack equations in order to increase the success prob-

ability. Assuming KL

[15 − 9] = 0x7 f , the seven

kinds of 1-bit attack equations are written as

A∈V

(38)

{FO

[63 − 32]; KO

,KO

)[i] ⊕

−1

(X ⊕A);KL

)[i]} = 0,

[63 − 32] = FL

−1

(X ⊕A);KL

,KL

)

(17)

where 25 ≤ i ≤ 31. Each 1-bit attack equation holds

with probability 2

−1

. Using those equations, we can

determine the key with probability 1 − 2

−7

, which

means KL

[15 − 9] 6= 0x00. Otherwise we can de-

termine KL

[15 − 9] = 0x00.

After linearization of the attack equation which

consists of 7-bits width, we obtain the total number

of unknown variables L = 1665 in a system of lin-

ear equations. If any of the unknown variables have

linear sum relations, the complexity for attack can

be reduced. In this paper, we chose independent un-

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

240

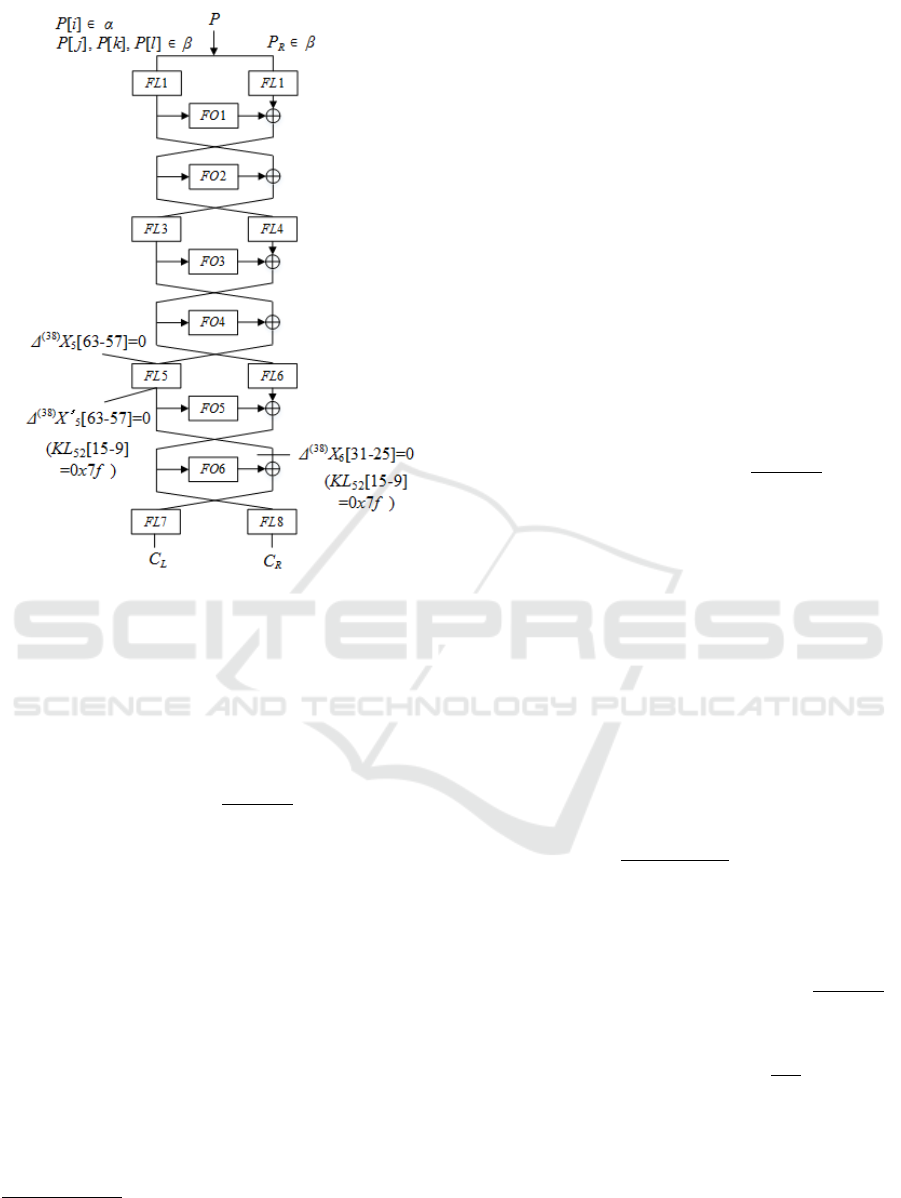
Figure 3: An attack on 6-round MISTY1 by using 38-th

order differential.

known variables

l = 189 as worst-case. Because ev-

ery linearized attack equation was derived by 1-bit

key KL

[i] assumption, additional 10 linear equa-

tions are needed to remove all false keys. From equa-

tion (10), the necessary number of chosen plaintexts

D is estimated as

D = 2



189 + 10



where m = 1 since the attack solves equation (17) for

each bit. Namely, D = 2

× 199 ≈ 2

45.7

. Here, we

can reduce the number of plaintexts D as follows. Let

us consider a 43-rd order differential denoted equa-

tion (18).

P =

{

P[i] ∈ α,P[ j,k,l], P

∈ β | i 6= j, k, l, j =k+16

}

k = h

,∼, h

(32 ≤ h

< h

≤ 38)

l = h

(32 ≤ h

≤ 38, or 48 ≤ h

≤ 54)

(18)

A 43-rd order differential described in equation (18)

can be used to construct 2





=320 sets of 38-th or-

der differential. The explanation is as follows. The

combination of choosing variable bit sub-blocks of

38-th order differential in equation (18) is





, be-

cause we have to choose 3-bits from (h

,∼, h

) as

It should be noted that the number of independent un-

known variables depends on the exact bit in attack equation.

See (Y. Tsunoo and Kawabata, 2008) in detail.

variable bit sub-blocks. When we regard one set of

43-rd order differential as some sets of 38-th order

differential, the number of ﬁxed bit sub-blocks in 43-

rd order differential is ﬁve. 5-bits pattern includes 2

possible values. Thus, a 43-rd order differential illus-

trated in equation (18) generates 2





=320 > 199

sets of 38-th order differential. Therefore, the neces-

sary number of chosen plaintexts D for key recovery

is estimated as 2

Now, we consider the time complexity for this at-

tack. The necessary computational cost for an attack

can be estimated as sum of the following 2-steps.

1. Preparation of ciphertexts

2. Key recovery

The time complexity for a preparation of ciphertexts

is estimated as 2

6-round MISTY1 encryptions.

From equation (11), the complexity for key recovery

is estimated as follows.

= 2

× (1665 + 1) ×



189 + 10



We can reduce the complexity by using a modulo 2

frequency distribution table. This table counts cipher-

text values appearing an odd number of times since

performing an XOR operation on the same value an

even number of times results in a value of 0. We pre-

pare 2 kinds of tables whose size are 2

with respect

to 18-bits C

[32 − 23,15 − 7] for 2 S9-boxes and 2

with respect to 14-bits C

[22 − 16, 6 − 0] for 2 S7-

boxes respectively. The cost for generating these ta-

bles is

= 2

× 2 × 199

table look-ups. If the computational cost for one table

look-up equals to the cost for a S7, S9 look-up, T

estimated as

× 2 × 199

6 × 9

≈ 2

40.9

encryptions because 6-round MISTY1 has 6 × 9 S-

boxes. The computational cost from equation (11) by

using these tables is estimated as

= (2 × 2

+ 2 × 2

) × (1665 + 1) ×



189 + 10



≈ 2

37.5

S-box look-ups. T

is estimated as

37.5

6×9

≈ 2

31.8

en-

cryptions. The complexity for solving a system of

equations resulting from linearization is negligible.

The overall time complexity T is estimated as

T = T

+ T

= 2

+ 2

40.9

+ 2

31.8

≈ 2

43.31

times of 6-round MISTY1 encryptions. The time

complexity T is dominated by the encryption of plain-

texts.

A Practical-time Attack on Reduced-round MISTY1

241

6 CONCLUSIONS

In this paper, we focused on evaluating the security of

MISTY1 in terms of practical-time complexity. We

implemented the 46th-order differential characteris-

tic for 4-round MISTY1 introduced in (Y. Tsunoo

and Kawabata, 2008) on a computer which mounts

GPU co-processors. We found 16-bits of 46-th order

differential characteristic was 0. We discovered the

new 38-th order differential characteristic for 4-round

MISTY1 whose characteristic is equal to the charac-

teristic estimated in (Y. Tsunoo and Kawabata, 2008).

We applied the 38-th order differential character-

istic to attack 6-round MISTY1 with 4 FL layers. The

complexity for attack needs 2

chosen plaintexts and

43.31

encryptions. By using 38-th order differential,

we can reduce the necessary number of data and time

complexity for an attack on 6-round MISTY1 with 4

FL layers by a factor of 2

. This is the best practical-

time attack on 6-round MISTY1.

REFERENCES

Bar-On, A. (2015a). A 2

attack on the full misty1. In

IACR ePrint Archive, 2015/746. IACR.

Bar-On, A. (2015b). Improved higher-order dierential at-

tacks on misty1. In Fast Software Encryption 22nd

International Workshop. Springer.

CRYPTREC (2013). CRYPTREC ciphers list,

http://www.cryptrec.go.jp/english/method.html.

Dunkelman, O. and Keller, N. (2008). An improved im-

possible differential attack on misty1. In ASIACRYPT,

volume 5350 of LNCS, pages 441-454. Springer.

Dunkelman, O. and Keller, N. (2013). Practical-time attacks

against reduced variants of misty1. In IACR ePrint

Archive, 2013/431. IACR.

H. Tanaka, K. H. and Kaneko, T. (1999). Strength of misty1

without ﬂ function for higher order differential attack.

In Applied Algebra, Algebraic Algorithms and Error-

Correcting Codes, volume 1719 of LNCS, pp 221-230.

Springer.

Igarashi, Y. and Kaneko, T. (2008). The 32nd-order differ-

ential attack on misty1 without ﬂ functions. In 2008

International Symposium on Information Theory and

its Applications, No.W-TI-4-4, pages 1503-1508. IE-

ICE.

ISO (2010). ISO/IEC 18033-3 information technology -

security techniques - encryption algorithms - part 3:

Block ciphers.

Jia, K. and Li, L. (2012). Impossible differential at-

tacks on reduced-round misty1. In 13th International

Workshop, WISA, volume 7690 of LNCS pages 1527.

Springer.

Lai, X. (1994). Higher order derivatives and differential

cryptanalysis. In Communications and Cryptography,

pages 227-233.

Matsui, M. (1997). New block encryption algorithm misty.

In Fast Software Encryption 4th International Work-

shop. Springer.

T. Shimoyama, Siho Moriai, T. K. and Tsujii, S. (1999). Im-

proving higher order differential attack and its appli-

cation to nyberg-knudesen’s designed block cipher. In

IEIEC Transactions, Fundamentals, Vol.E82-A, No.9,

pages 1971-1980. IEICE.

Todo, Y. (2015). Integral cryptanalysis on full misty1. In

CRYPTO 2015 volume 9215 of LNCS, pages 413-432.

Springer.

Y. Hatano, H. T. and Kaneko, T. (2004). Optimization

for the algebraic method and its application to an at-

tack of misty1. In IEIEC Transactions, Fundamentals,

Vol.E87-A, No.1, pages 18-27. IEICE.

Y. Tsunoo, Teruo Saito, M. S. and Kawabata, T. (2008).

Higher order differential attacks on reduced-round

misty1. In ICISC, volume 5461 of LNCS, pages 415-

431. Springer.

Yi, W. and Chen, S. (2014). Multidimensional zero-

correlation linear attacks on reduced-round misty1. In

CoRR, abs/1410.4312.

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

242