An Industry-focused Advertising Model
A. Murray
Department of Applied Mathematics, The University of Western Ontario, 1151 Richmond St. North, London, Canada
Keywords:
Optimal Control, Advertising, Stochastic Optimal Control, Mathematical Modelling.
Abstract:
In this paper a model is created that may be effectively used to determine the optimal spending trajectory for
an advertising campaign. Given a sufficient data set, all parameters present in the model should be easily
determinable, or at least accurately approximated, and justifications are given for the form of all parts of the
model. Finally, the solution to both the deterministic and stochastic versions of the model are given.
1 INTRODUCTION
The problem of predicting whether an ad campaign
will ultimately be successful is an important prob-
lem that is difficult to solve. Several models have al-
ready been proposed such as the Sethi model (Sethi,
1983) and the older Vidale-Wolfe advertising model
(Vidale and Wolfe, 1957). However, all advertising
models thus far have been purely theoretical and have
had limited applicability due to their assumptions and
simplifications. Justifications for each feature of the
new model come from a large data set provided by
a corporation that is actively engaged in numerous
advertising campaigns, however it has not been pre-
sented here due to confidentality issues.
Since (Gould, 1970) it has become standard prac-
tice to assume that the function relating market share
to advertising effort is concave. Indeed, it would
be unreasonable to assume differently as that would
imply that there would not be a diminished effect
from each additional advertisement. However, the
exact nature of the relationship between advertising
effort and market share is often quite difficult to de-
termine due to the inherent variance in this type of
data. Typically there is so much variance that almost
any concave function would model the relationship
quite well. Lewis and Rao (Lewis and Rao, shed)
demonstrate the difficulty in simply proving that a
given advertising campaign yielded a positive return
on investment, let alone the relationship between ad-
vertising spending and the resulting growth in market
share. Thus, a quadratic relationship between market
share and advertising expenditure is assumed since a
quadratic form yields a very simple form for the opti-
mal control. The purpose of the new model is to max-
imize long-term profit, however future profits must be
”discounted” due to the role that re-investment and in-
flation play. This effect is incorporated into the model
by multiplying the profit at time t by e
−δt
, where δ
is the rate at which the profit is discounted over time.
Thus the long-term profit can be described according
to the following function:
P =
∞
∑
0
(mx
t
−u
2
t
)e
−δt
. (1)
Where x
t
is the market share at time t, m is the rev-
enue per unit of market share, and u
t
is the advertising
effort at time t.
As in the Sethi model, x
t
is normalized by the mar-
ket share, however unlike the Sethi model the size
of the market does not remain constant. Instead, it
is assumed that the market size changes according to
the predefined function M
t
. Modelling market growth
and decline is a separate problem and no attempt to
do so is undertaken in this paper. The dynamics of
the market share are modelled as a discrete version of
those found in Equation 5 of (Murray and MacIsaac,
2015). A discrete model is used since firms cannot
feasibly control their advertising expenditure in real
time but only for periods of time with granularity
on the order of months, days, hours, etc. Equation
2 gives the deterministic version of the function de-
scribing the dynamics of the state equation where ρ
is the effectiveness of advertising, and D is the rate at
which market share decays (assumed to be linear for
simplicity).
x
t+1
−x
t
= ρu
t
√
M
t
−x
t
+ r(x
t
)(M
t
−x
t
) −Dx
t
, (2)
where 0 ≤ x
t
≤ M
t
. It is known that the function
describing the decay of the market share is concave
Murray, A.
An Industry-focused Advertising Model.
DOI: 10.5220/0005653300870091
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 87-91
ISBN: 978-989-758-171-7
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
87

however a quadratic relationship (−
Dx
2
2
) once again
results in the simplest optimal control. The growth
due to ranking, r(x
t
) is defined as follows:
r(x
t
) =









r
k
, if x
t
≥ T
k
,
. . .
r
1
, if T
2
> x
t
≥ T
1
,
0, otherwise
which captures the effect that ranking systems have
on market share growth. Each T
i
is the market share
threshold to enter into the i
th
ranking tier. As the mar-
ket share grows, so too will the ranking and likewise
a higher ranking spurs more growth. For more in-
formation on the dynamics of the ranking system see
(Murray and MacIsaac, 2015). In equation 1 it has
been assumed that the rankings are in a state of equi-
librium and thus have taken it to only be dependent
on the market share. In general, the advertising rate
of each company will affect their rankings and thus
affect the rankings of other firms as well. For more
research on the optimization of advertising revenue in
a system with many competing firms see (Fruchter,
1999), (Horsky, 1988) and (Erickson, 1995).
2 DETERMINISTIC SOLUTION
The current value Hamiltonian from equations 1 and
2 is
H = mx
t
−u
2
t
+λ(ρu
t
√
M
t
−x
t
+r(x
t
)(M
t
−x
t
)−Dx
t
),
(3)
which is almost identical to what is seen in the Sethi
model. Indeed, the optimal control takes a similar
form to that of the Sethi model:
u
∗
(x) =
λρ
√
M −x
2
. (4)
If we attempt to derive λ while taking r to depend
on x then the solution becomes intractable. However,
by Bellman’s Optimality Principle (Bellman, 1957),
each sub-path of an optimal path must be optimal.
Thus, for each interval where r is constant a solution
may be obtained. By solving equation 5, for a par-
ticular value of r, we can determine the current value
adjoint variable λ
t
.
λ
t+1
−λ
t
=
−dH
dx
= −m+λ

D + δ + r +
ρu
∗
2
√
M −x

.
(5)
When equation 4 is substituted into equation 5 we get:
λ
t+1
−λ
t
=
−dH
dx
= −m + λ

D + δ + r +
ρ
2
λ
4

,
(6)
which is a Ricatti Equation. The optimal path will re-
quire λ(0) = lim
t→∞
λ
t
. The optimal long term equi-
librium of λ
t
can be determined by setting λ
t+1
−λ
t
=
0 and solving for λ
t
in equation 6. The solution to
which is
lim
t→∞
λ
t
=
−2(D + r + δ −A))
ρ
2
(7)
where A =
p
2mρ
2
+ (r + D + δ)
2
. Solving equation
6 with the initial condition λ(0) = lim
t→∞
λ
t
yields
λ
t
=
−2(D + r + δ −A)
ρ
2
. (8)
If equation 2 is evaluated with the lambda obtained in
equation 8 then we get
x
t+1
−x
t
=
λρ
2
(M −x
t
)
2
+ r(M −x
t
) −Dx
t
. (9)
The solution of equation 9 with initial condition
x(0) = x
0
is
x
t
= (x
0
−
M(λρ
2
+ 2r)
B
)e
−Bt
2
+
M(λρ
2
+ 2r)
B
. (10)
For a particular value of r where B = 2D + λρ
2
+ 2r.
The full, piece-wise optimal path of x
t
is given by
x
t
=









x
t
|
r=r
k
, if x
−1
(T
k
) ≤t
. . .
x
t
|
r=r
1
, if x
−1
(T
1
) ≤t < x
−1
(T
2
)
x
t
|
r=0
, otherwise
If equation 8 is substituted into equation 4 then the
following optimal feedback control is obtained:
u∗
t
=
−(D + r + δ −A)
√
M −x
t
ρ
. (11)
Figure 1 illustrates how the state and control func-
tions change when ranking is introduced. The dra-
matic decreases in the optimal advertising rate are due
to each changes in ranking.
The y-axis for x(t) is market share and the y-axis
for u(t) is measured in arbitrary cost units. The mar-
ket in Figure 1 is being modelled as growing linearly
at a very slow rate, but is still visible in the upward
bend in the optimal state and control functions.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
88

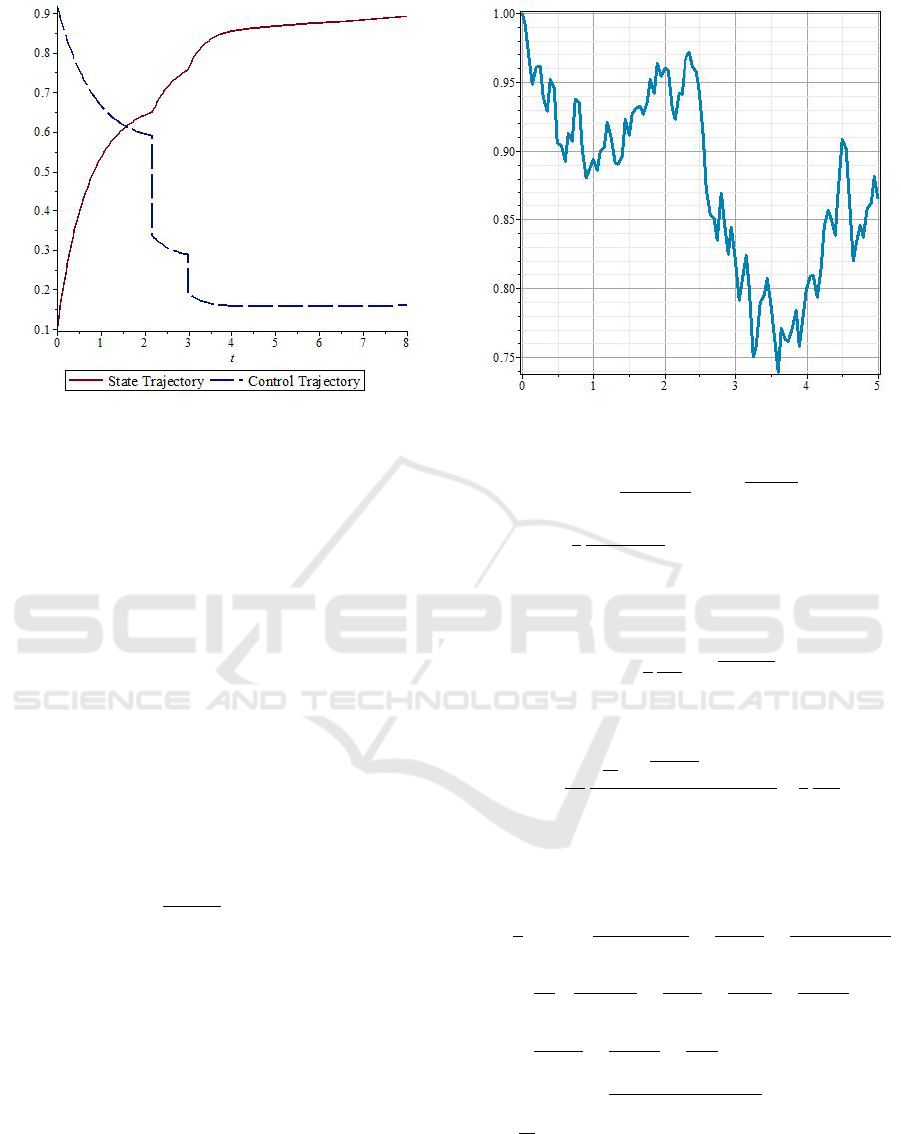
Figure 1: Comparison of x(t) and u(t) in the deterministic
case.
3 STOCHASTIC SOLUTION
A major departure from previous advertising models
is made by incorportating dynamics into the effective-
ness of advertising. While the effectiveness, ρ is tra-
ditionally treated as a constant it will be assumed that
ρ evolves randomly through time according to a white
noise process w(ρ
t
). Doing so takes into account ef-
fects like competing ads, changing ad ”creatives” and
other phenomenon that may impact how receptive an
audience is to a given ad campaign. It should be
noted that multiple competing firms would be more
accurately modelled by a many-player game theoretic
approach as seen in (Prasad and Sethi, 2004). The
stochastic model that will be used is similar to Equa-
tion 2,
x
t+1
−x
t
= ρ
t
u
t
√
M
t
−x
t
+ r(x
t
)(M
t
−x
t
) −Dx
t
,
(12)
however it includes the following dynamics:
ρ
t+1
−ρ
t
= w(ρ
t
). (13)
Where ρ(0) = ρ
0
and as in Section 1, 0 ≤ x
t
≤ M
t
∀t
and x(0) = x
0
. Again we seek to maximize equation
1 but first we solve for the Value function V (x
t
, ρ
t
).
Note that we need not make restrictions on the parity
of ρ
t
and indeed, a negative value for advertising ef-
fectiveness could be interpreted as a poor public view
of the firm and/or its products. Shown in Figure 2 is a
sample path for how ρ
t
may vary over time.
By (Bensoussan, 1982) the current-value function
for this problem satisfies the following HJB equation:
Figure 2: A sample path for the advertising effectiveness
over time.
δV (x
t
, ρ
t
) = max
u
t

∂V (x
t
, ρ
t
)
∂x
t
(ρ
t
u
t
√
M
t
−x
t
−Dx
t
+ r)+
1
2
∂
2
V (x
t
, ρ
t
)
∂ρ
2
t
w
2
(ρ
t
) + mx
t
−u
2
t

.
(14)
It can be easily verified that the optimal control for
this case is:
u
t
∗ =
1
2
∂V
∂x
t
ρ
t
√
M
t
−x
t
. (15)
Substituting equation 15 into equation 14 yields
δV = mx
t
+
∂V
∂x
t

∂V
∂x
t
ρ
2
t
√
M
t
−x
t
−Dx
t
+ r

4
+
1
2
∂
2
V
∂ρ
2
t
w
2
(ρ
t
).
(16)
The details of the solution to equation 16 are left out
for the sake of brevity, however the result is
V =
1
δ

mx
t
+
G
2
t
(M
t
−x
t
)
4ρ
2
t
−
G
t
Dx
t
ρ
2
t
+
G
t
r(M
t
−x
t
)
ρ
2
t
+
σ
2
2

−2m
2
x
t
H
3
t
−
6mx
t
ρ
2
t
H
t
+
6G
t
x
t
ρ
4
t
+
2m
2
ρ
t
δH
2
t
−
5G
t
m
ρ
3
t
δH
t
−
G
t
m
2
ρ
t
δH
3
t
+
3G
2
t
ρ
5
t
δ

(17)
where G
t
= 2(
p
(δ + D + r)
2
+ mρ
2
t
−δ −D −r) and
H
t
=
G
t
2
+ δ + D + r. Inserting equation 17 into equa-
tion 15 yields the optimal feedback control for the
stochastic problem as shown in equation 18.
An Industry-focused Advertising Model
89

u
t
∗ =
1
2δ

m −
G
2
t
4ρ
2
t
−
G
t
D
ρ
2
t
−
G
t
r
ρ
2
t
+ σ
2

3G
t
ρ
4
t
−
m
2
H
3
t
−
3m
ρ
2
t
H
t

ρ
t
√
M
t
−x
t
(18)
Figure 3 is a sample path for the stochastic optimal
feedback control using the advertising effectiveness
path seen in Figure 2.
Figure 3: A sample path for optimal advertising spending
over time.
4 CONCLUSION
Both the deterministic and stochastic problems have
been solved and although the form of the optimal
control in the stochastic case is quite complex, it is
still straight-forward to implement computationally,
allowing advertisers to automate their spending on as
granular a level as is feasible. Shown below is a com-
parison of the controls for the stochastic versions of
the Sethi model and the model presented in this pa-
per.
Although the discrete nature of the model does not
impact the form of the optimal control, it has been
formulated in this way to be more immediately ap-
plicable to problems in industry. As Figure 4 illus-
trates, the ranking plays a large part in the difference
between the new and old forms of the optimal control.
A more subtle difference comes from the non-
constant size of the market. In Figures 1, 3 and 4
the market was assumed to slightly grow at a constant
rate. This is most noticeable in the tail of the functions
shown in Figure 1, however Figure 5 exaggerates the
growth to demostrate the impact that a non-constant
Figure 4: Sample paths for optimal advertising spending
over time under the Sethi model (upper path) and new
model (lower path).
Figure 5: Sample paths for optimal advertising spending
over time under the Sethi model and new model where the
new model assumes a large linear growth in the market over
time.
market has on the optimal control. In well-established
industries the non-constant market will not likely play
a very big part in determining the advertising budget.
However, if the market is either quickly exanding or
quickly diminishing then this must be taken into ac-
count when determining the advertising strategy and
the models presented in this paper dictate such a strat-
egy.
The models presented in this paper could be ex-
tended to allow for interactions between advertisers,
although the budgets and spending of competing ad-
vertisers is not typically known and thus such an ex-
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
90

tension would serve as a largely theoretical exercise.
However, Chintagunta and Vilcassim (Chintagunta
and Vilcassim, 1992) show that if each player only
has knowledge of the past strategies of their opponent
then the resulting optimal control formulation more
closely aligns with what is empirically observed. Fur-
thermore, the interaction between advertising and the
market could be explored. If the market is defined as
the set of people who would be willing to purchase the
product then for nascent industries the market would
be quite small, but could be expanded through adver-
tising efforts.
REFERENCES
Bellman, R. (1957). Dynamic Programming. Princeton
University Press.
Bensoussan, A. (1982). Stochastic Control by Functional
Analysis Methods. North-Holland Publishing, New
York.
Chintagunta, P. and Vilcassim, N. (1992). An empirical
investigation of advertising strategies in a dynamic
duopoly. Management Science, 38:1230–1244.
Erickson, G. (1995). Advertising strategies in a dynamic
oligopoly. Journal of Marketing Research, 32:23–237.
Fruchter, G. (1999). The many-player advertising game.
Management Science, 45:1609–1611.
Gould, J. (1970). Diffusion processes and optimal advertis-
ing policy.
Horsky, D. (1988). Dynamic advertising strategies of com-
peting durable good producers. Marketing Science,
7:356–367.
Lewis, R. and Rao, J. (accepted, soon to be published). On
the near impossibility of measuring the returns to ad-
vertising. Quarterly Journal of Economics.
Murray, A. and MacIsaac, A. (2015). Extension of the sethi
model to the advertising of digital products. In SIAM
CT15, Control & its Applications.
Prasad, A. and Sethi, S. (2004). Competitive advertising
under uncertainty: A stochastic differential game ap-
proach. Journal of Optimization Theory and Applica-
tions, 123:163–185.
Sethi, S. (1983). Deterministic and stochastic optimization
of a dynamic advertising model. Optimal Control and
Applications, 4:179–184.
Vidale, M. and Wolfe, H. (1957). An operations-research
study of sales response to advertising. Operations Re-
search, 5:370–381.
An Industry-focused Advertising Model
91