Similarity Assessment as a Dual Process Model

of Counting and Measuring

Bert Klauninger and Horst Eidenberger

Institute for Interactive Media Systems, Vienna University of Technology, Vienna, Austria

Keywords:

Dual Process Model, Similarity Assessment, Combined Kernels, Counting and Measuring, Quantisation,

Generalisation, Taxonomic and Thematic Reasoning, Image Similarity.

Abstract:

Based on recent ﬁndings from the ﬁeld of human similarity perception, we propose a dual process model

(DPM) of taxonomic and thematic similarity assessment which can be utilised in machine learning applica-

tions. Taxonomic reasoning is related to predicate based measures (counting) whereas thematic reasoning is

mostly associated with metric distances (measuring). We suggest a procedure that combines both processes

into a single similarity kernel. For each feature dimension of the observational data, an optimal measure is

selected by a Greedy algorithm: A set of possible measures is tested, and the one that leads to improved clas-

siﬁcation performance of the whole model is denoted. These measures are combined into a single SVM kernel

by means of generalisation (converting distances into similarities) and quantisation (applying predicate based

measures to interval scale data). We then demonstrate how to apply our model to a classiﬁcation problem

of MPEG-7 features from a test set of images. Evaluation shows that the performance of the DPM kernel is

superior to those of the standard SVM kernels. This supports our theory that the DPM comes closer to human

similarity judgment than any singular measure, and it motivates our suggestion to employ the DPM not only

in image retrieval but also in related tasks.

1 INTRODUCTION

We suggest an SVM kernel function for image re-

trieval that is based on the latest ﬁndings of psycho-

logical research on human similarity measurement.

Humans appear to derive their similarity judgments

from a mixture of thematic and taxonomic stimuli,

called a dual process model of similarity (DPM)

(Wisniewski and Bassok, 1999). Thematic stimuli

(e.g.general appearance in form of a global color his-

togram) are typically measured by distance functions,

taxonomic ones (e.g.co-existing properties such as

”person visible”) by similarity functions. The ﬁrst re-

quire the transformation from distance to similarity by

a so-called generalisation function. The latter require

the quantisation of numbers into predicates.

This paper provides the DPM kernel as well as

the necessary components, partly taken from earlier

work of the authors. The kernel is applied on a set

of MPEG-7 features computed for a test set of im-

ages. Evaluation shows that for the present task the

DPM kernel is superior to the standard SVM kernels

which proofs the concept as well as supports the men-

tioned psychological ﬁndings. We suggest to employ

the DPM kernel also on related tasks.

The next section introduces the model compo-

nents, including the generalisation model and the

quantisation model employed in the DPM kernel.

Section 3 explains the similarity model itself, eval-

uated and discussed in Section 4.

2 BACKGROUND

2.1 Measuring vs. Counting

Traditional mathematical models of human similarity

perception are often geometric ones (e.g.(Torgerson,

1952)): Observational data is mapped into some psy-

chological or mathematical space (usually a vector

space) in such a way that similar observations are pro-

jected into the same regions, thus constituting a metric

on that space.

In his 1977 paper (Tversky, 1977), psychologist

Amos Tversky proposed a different approach towards

similarity. After demonstrating that the metric axioms

are in fact violated in human similarity judgment, he

Klauninger, B. and Eidenberger, H.

Similarity Assessment as a Dual Process Model of Counting and Measuring.

DOI: 10.5220/0005655801410147

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 141-147

ISBN: 978-989-758-173-1

141

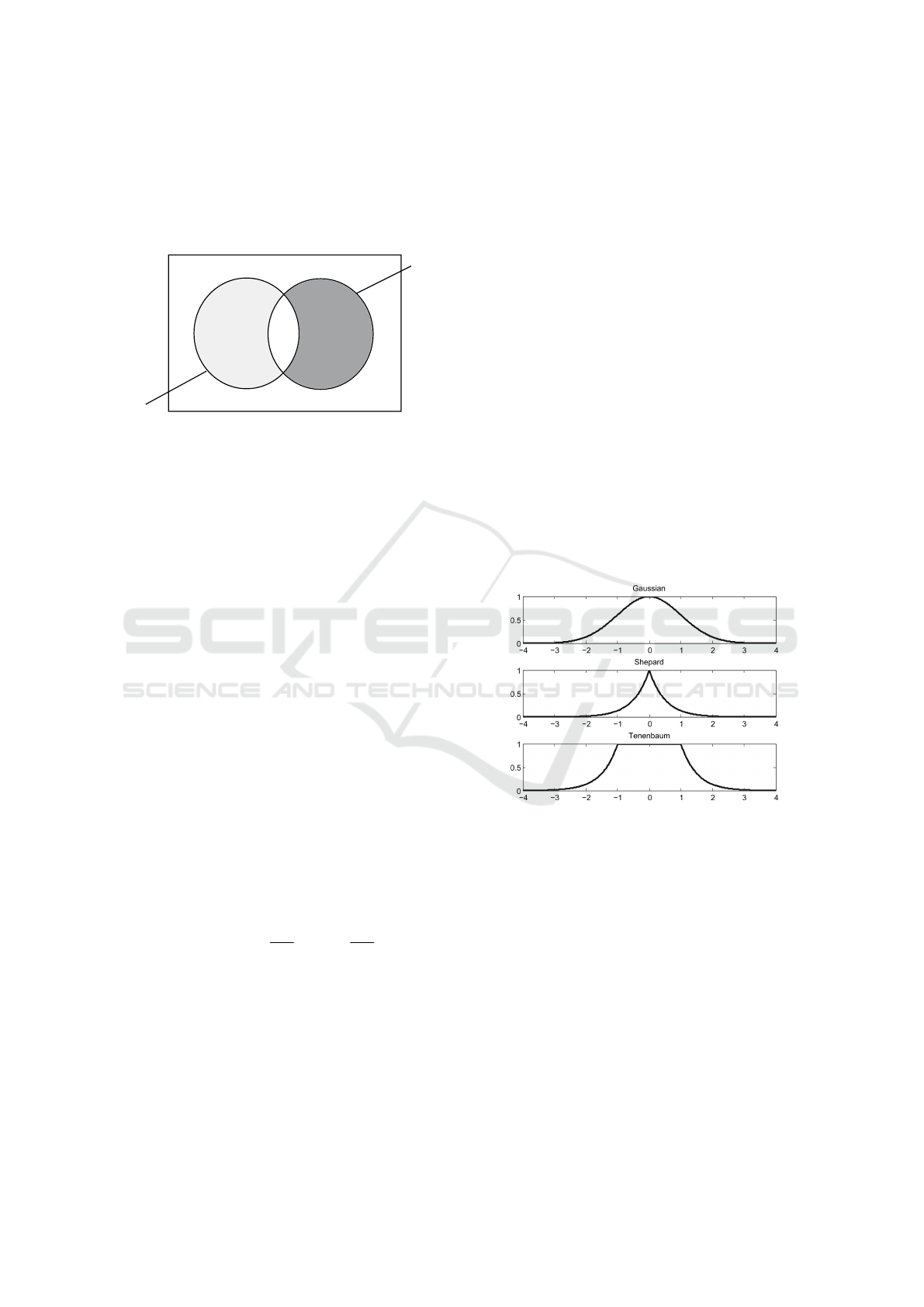
developed a set-theoretical framework that operates

in terms of matching and mismatching features rather

than metric distances. Observations are represented

as collection of features, and similarity is computed

by counting common and distinct features. Figure 1

Figure 1: Feature Contrast Model.

deﬁnes the building blocks of all predicate based sim-

ilarity measures: For two stimuli X ,Y : a = |X ∩Y |,

b = |X \Y |, c = |Y \ X|, and d = |M \ (X ∪Y )|. The

concept of similarity as counting gave birth to a vari-

ety of predicate based measures, as for example Tver-

sky’s Feature Contrast Model (FCM) itself, Jaccard’s

coefﬁcient, Kulczynski distance and many others.

Other existing measures were integrated in the model

(e.g.the Hamming distance). Both metric distances

and predicate-based measures are essential building

blocks of the DPM kernel deﬁned in Section 3.

2.2 Quantisation Model

In order to be able to apply predicate-based measures

to quantities, the set theoretical deﬁnition of predi-

cates has to be extended to the interval scale, i.e. each

feature dimension indicates that a property is more

or less present (0 means “not at all”, 1 means “fully

present”). One candidate would be the Fuzzy Feature

Contrast Model (see (Santini and Jain, 1999)) which

arguably suffers from some shortcomings. So, for our

purposes, we utilized the Quantisation Model (QM)

as described in (Eidenberger, 2003). This QM re-

places set theoretical predicate measures with statis-

tical functions in the following way:

a = |X ∩Y | :=

∑

(

if M −

<= ε

0 else

(1)

b = |X \Y | :=

∑

(

− y

if M − (x

− y

) <= ε

0 else

(2)

c = |Y \ X| :=

∑

(

− x

if M − (y

− x

) <= ε

0 else

(3)

with: ε

,ε

being two thresholds and M = 1 for

∈ [0,1]. Depending on the thresholds, two quanti-

ties are considered co-existing predicates if they are

both sufﬁciently large. Below, we employ this model

for the transformation of image features into count-

able taxonomic properties.

2.3 From Distance to Similarity:

Generalisation

Intuitively, one would deﬁne similarity as some kind

of “inverse distance”: The more similar two stimuli

are, the smaller their distance in an appropriate psy-

chological space should be. A function that estimates

similarities from distances is called a generalisation

function.

In (Shepard, 1987), Shepard carefully examined

different candidates and came to the conclusion that

the probability P(R

) that a stimulus S

is associ-

ated with a response R

is proportional to e

−δ

x,y

, δ be-

ing the distance between representations x and y in an

appropriate space (Shepard, 1987). This relation is

known as the Universal Law of Generalisation.

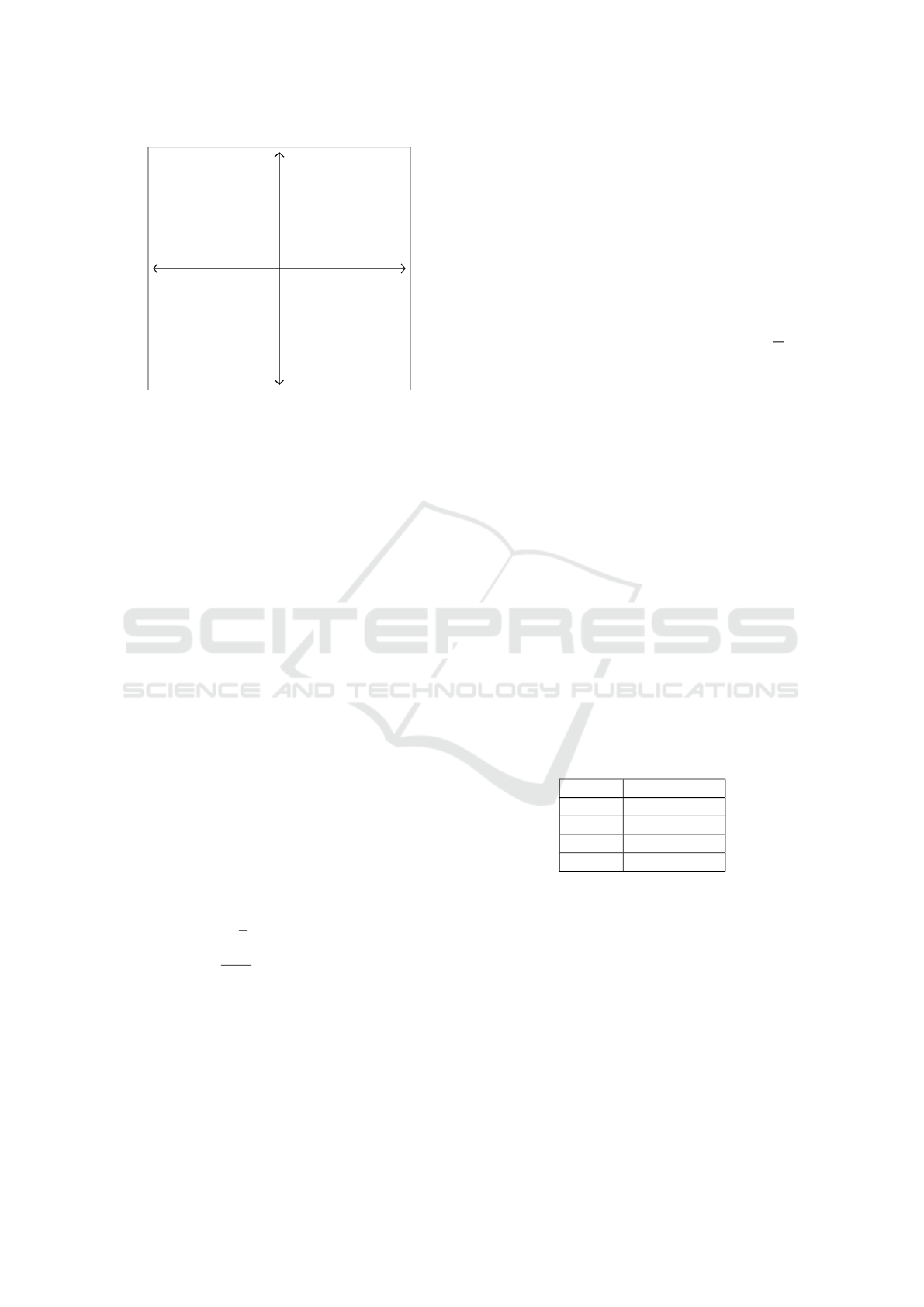
Figure 2: Three Generalisation Functions.

While Shepard’s law holds on some classes of data

sets, there are others that violate it (Chater and Vitnyi,

2003, p.349). In some cases, a Gaussian density func-

tion, where P(R

) is proportional to e

−δ

x,y

, has

been applied more successful. Another generalisation

function has been proposed by Tenenbaum and Grif-

ﬁths (Tenenbaum and Grifﬁths, 2001) as an extension

of the Universal Law to generalising from multiple

consequential stimuli. In the DPM kernel, we employ

a generalisation function to transform distance values

into thematic similarities that can be combined with

taxonomic properties.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

142

2.4 General Dual Process Model

For the deﬁnition of our DPM kernel function, we

employ the simple model suggested in (Eidenberger,

2012, p.540):

d pm

= α.m

tax

+ (1 − α)g(m

them

) (4)

Here, m

tax

stands for taxonomic measures which

are usually similarities (e.g.co-occurrences, cosine

similarity); m

them

stands for the thematic aspects

expressed in image features which are usually dis-

tances (e.g.Hamming distance, city block metric); g

is the generalisation function (Gaussian, Tenenbaum

or Shepard).

Linear combinations with α are capable of repre-

senting any other similarity measurement. α itself is

deﬁned by the user’s preference toward taxonomic vs.

thematic reasoning which could be estimated in psy-

chological tests.

3 MATERIALS AND METHODS

3.1 An Integrative Image of Similarity

Our hypothesis is that, in order to construct an ideal

global similarity measure for a given dataset, differ-

ent feature dimensions may require different similar-

ity functions. The list of possible kernel functions can

be aligned at two dimensions (see Figure 3), reﬂecting

current ﬁndings from psychology on human similar-

ity perception: the continuum from similarities (sep-

arable stimuli) to distances (integral stimuli) on one

hand, and the continuum from predicate-based (tax-

onomic) to quantitative (thematic) reasoning on the

other hand.

separable

integral

similarity distance

thematic quantities

taxonomic predicates

similarity measurement

Figure 3: Axes of Similarity Assessment.

3.2 Greedy Algorithm

If we accept the model described above, the question

arises how to determine which feature dimensions are

best compared by which measure. For a pair of im-

ages, we could use some a-priori knowledge about the

semantic meaning of the dimension, e.g.the feature

“global color histogram” would most likely be com-

pared using a quantitative measure (e.g.earth mover’s

distance), whereas for the taxonomic feature “face

visible” it would make sense to use some predicate-

based measure.

In absence of such a-priori knowledge, we could

try out several measures for each dimension, evalu-

ate the model and denote the measure that yields the

best global result during the evaluation process. Such

a heuristic is known as Greedy algorithm: We are

able to approximate the globally optimal solution by

making locally optimal choices (Cormen et al., 2009,

p.424f). In contrast to Dynamic Programming where

each sub-problem is optimised separately and then

combined, our algorithm evaluates the whole problem

in each step.

Ideally, the dimensions should be uncorrelated. In

practice, this is usually not the case. Hence the or-

der in which the dimensions were processed had been

randomised.

3.3 Our Model

There is a vast variety of similarities, distances, corre-

lations and divergences that have been proposed in lit-

erature. A classiﬁcation into thematic and taxonomic

measures can be established in the following way: If

the formula contains a contrast term in the formula

(x − y,

−a

), then it is considered the-

matic, otherwise taxonomic.

In order to capture the two-dimensional frame-

work of similarities vs. distances and predicates vs.

quantities, we focused on four candidates that repre-

sent extremes in the continuum of possible measures

(see ﬁgure 4):

1. Dot Product: separable stimuli, thematic reason-

ing

2. Number of co-occurrences: separable stimuli,

taxonomic reasoning

3. L

distance: integral stimuli, thematic reasoning

4. Hamming distance: integral stimuli, taxonomic

reasoning

The inner product or dot product of two vectors is

equivalent to applying the cosine similarity measure

on [0, 1] normalised data. It compares two vectors in

Similarity Assessment as a Dual Process Model of Counting and Measuring

143

Quantisation Model

Dual Process Model

dot product

distance

co-occurrences Hamming distance

Figure 4: Chosen Measures.

respect of the angle between them: identical vectors

result in a score of 1, orthogonal vectors (θ = 90

◦

)

give a score of 0. This measure has successfully

been applied to ﬁelds like document retrieval and data

mining (e.g.(Salton et al., 1975), (Faloutsos and Lin,

1995)).

In counting the co-occurrences, only those predi-

cates which are present in both sets X and Y are taken

into account. Applied to the Quantisation Model (2),

this means that those vector components contribute

more to the result that have high values in both vec-

tors.

Minkowski distances L

are appropriate for ob-

servations in the form of numeric measurements

(e.g.measures of geometrical or physical properties).

They have been used in models of similarity assess-

ment for a very long time (e.g.(Torgerson, 1952)).

The city block distance L

was chosen for its com-

putational effectiveness.

The Hamming distance is deﬁned as the number

of different bits in two binary vectors, or set theoreti-

cally, as the number of elements that are either present

in X or in Y , but not in both of them. Quantisation

of this measure leads to a distance where large dif-

ferences in vector components contribute more to the

result than small ones.

The dual process Model can now be written as:

d pm

(X,Y ) =

) + m

))+

1 − α

g(m

) + m

))

(5)

with:

(~x,~y) =~x ·~y

(~x,~y) = a(~x,~y)

(~x,~y) = L

(~x,~y) =

∑

i=1

− y

(~x,~y) = b(~x,~y) + c(~x,~y)

and Y

being the sub-vectors consisting of those

components that had been determined to go best with

measure m

by the Greedy algorithm. For general-

isation g, the Gaussian function g(x) = e

−0.5x

was

selected empirically. a, b and c are computed using

the QM (Equations 1, 2 and 3).

Three parameters go into the model: The param-

eter α ∈ [0, 1] is used to move bias from taxonomic

to thematic stimuli, and the parameters ε

determine

the “hardness” of quantisation of the predicate-based

measures. In our experiments, α was set to

, k

being the number of feature dimensions that are re-

garded rather separable than integral (by the Greedy

algorithm), and k being the total number of dimen-

sions. The quantisation thresholds were tuned heuris-

tically.

4 TESTS AND RESULTS

4.1 Test Set

Our test set consists of 426 instances of MPEG-7 de-

scriptions from images depicting coats of arms. The

images are described by 314 dimensions from CL,

CSD, DC, EH, HT, RS, SC and TB descriptors. All

components were normalised to [0, 1] beforehand.

Ground truth has been provided by manual annota-

tion. Each instance falls into one of ﬁve highly seman-

tic categories (e.g.”Bavarian city arms”) with vastly

different sizes (table 1) – to make the machine learn-

ing problem harder.

Table 1: Class Sizes.

Class 1 1 instance

Class 2 20 instances

Class 3 34 instances

Class 4 51 instances

Class 5 320 instances

Hence this can be considered a difﬁcult set for

training classiﬁers in general. Another reason for

choosing this dataset was the hope that, by de-

sign, some features would be more likely to ﬁt into

predicate-based than in quantitative measurement.

Figure 5 shows some examples of value distributions

for different features. The numbers above the his-

tograms denote the corresponding feature dimension.

We suspected that features with a continuous spec-

trum are best compared using quantitative measures

whereas features with a small number of sharp peaks

can be interpreted as sets of predicates, one for each

peak.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

144

Figure 5: Example of Feature Dimensions with Different

Distributions.

4.2 Test Pipeline

In our experiment, classiﬁers should be trained that

predict the class label of an input vector with high

conﬁdence. Support Vector Machines (SVM) were

chosen because similarity measures can be directly

applied as kernels, and because they are fairly efﬁ-

cient in respect to computational cost. In order to ex-

tend the SVM concept to a multi-class problem, the

approach of one-vs-one (Milgram et al., 2006) was

implemented.

Usually, one would reduce the dimensionality,

e.g.by means of PCA or SVD, but for our experiment,

we decided to omit this step in order to keep full

diagnosticity for each dimension.

The experimental setting was as follows:

1. Input data (observation vectors and ground truth)

is read in and randomly divided into training and

test set (using a holdout of 50%).

2. From the training set, for each feature dimension

in random order, m

, m

and m

is tried out by

the Greedy algorithm: At each step, a set of SVMs

is trained one-by-one, using DPM similarity as

kernel. The resulting classiﬁer is cross-validated

on the test set. From the four possibilities, that

measure which yields the best classiﬁcation result

(maximal global F

score) is kept for this dimen-

sion.

3. In the end, a DPM similarity kernel is obtained

that is approximately optimal.

4. The performance of this DPM kernel is compared

to single kernels (linear, quadratic, polynomial,

Radial Base Function) in terms of precision, re-

call, fallout and F

score, per class and averaged.

Evaluation was performed in terms of precision,

recall, fallout and F

score, per class and globally.

For global performance estimation of a model, macro-

averaging of the per-class results was used as pro-

posed by Yang and Liu, albeit in the context of text

categorisation (Yang and Liu, 1999):

global

∑

i=1

(i)

, k is the number of classes (6)

4.3 Results

Figure 6 shows the precision-recall curves for each

class, collected from ten test runs. One ﬁgure is given

per kernel type. As can be seen, the DPM kernel and

the linear kernel come closest to the optimal recall and

precision (upper right corner of the ﬁgures).

Tables 2 contain the performance indicators,

macro-averaged over all classes, hence equally penal-

ising classiﬁcation error rates among classes of differ-

ent size.

Table 2: Averaged Global Performance.

linear quadratic polynomial

avg. precision 0.4598 0.4132 0.3043

avg. recall 0.3914 0.2688 0.2173

avg. fallout 0.1370 0.1704 0.1933

avg. F

score 0.4131 0.2829 0.2058

RBF DPM

avg. precision 0.1509 0.5823

avg. recall 0.2000 0.4446

avg. fallout 0.2000 0.1112

avg. F

score 0.1720 0.4836

4.4 Discussion

Our experiments demonstrate that, for our data set of

MPEG-7 features, the Dual Process Model as trained

by the Greedy algorithm performs always better that

the best singular kernel (which was the linear kernel

in all cases). In numbers, global average precision

of the DPM kernel is 26.66% higher than for the lin-

ear kernel, recall is 13.58% higher, fallout is 12.41%

lower, and F

score is 17.07% higher.

Quadratic and polynomial kernels performed a lit-

tle worse than the linear one, and RBF had the prob-

lem of always associating all instances to the same

class, namely the largest one. This is an interesting

ﬁnding per se. Arguably, RBF by design works well

in classiﬁcation problems where class sizes are in the

same order of magnitude, but cannot cope with very

unequally sized classes.

In terms of classes, it is obvious that class 1 (only

one class member) failed in all models, whereas class

5 (the largest one) performed best with precision, re-

call and F

values close to 1.0. Regarding the smaller

classes 2 to 4, the discriminative power of the DPM

kernel comes into play. Here the DPM has always per-

formed better in terms of recall, precision and fallout

than all other kernels under consideration.

Similarity Assessment as a Dual Process Model of Counting and Measuring

145

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

0,0

0,2

0,4

0,6

0,8

1,0

Linear Kernel

class1

class2

class3

class4

class5

Precis ion

Recall

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

0,0

0,2

0,4

0,6

0,8

1,0

Quadratic Kernel

class1

class2

class3

class4

class5

Precis ion

Recall

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

0,0

0,2

0,4

0,6

0,8

1,0

Polynomial Kernel

class1

class2

class3

class4

class5

Precis ion

Recall

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

0,0

0,2

0,4

0,6

0,8

1,0

RBF Kernel

class1

class2

class3

class4

class5

Precis ion

Recall

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

0,0

0,2

0,4

0,6

0,8

1,0

Dual Process Model

class1

class2

class3

class4

class5

Precis ion

Recall

Figure 6: Performance of Different Kernels per Class.

5 CONCLUSIONS AND FUTURE

WORK

The experimental results presented in section 4 sup-

port the hypothesis that a dual process model of sep-

arable and integral stimuli, comprising both geomet-

ric and quantised predicate based similarity measures,

comes closer to human judgment (ground truth) than

the best single measures. The validity of our sim-

ple DPM (equation 4) has been demonstrated and

thus provided the motivation to direct future research

activity towards developing a universal DPM frame-

work for similarity assessment.

For future work, we expect that the value distri-

bution of a feature can give important clues about the

kind of similarity measure best applied to it. We will

endeavor to identify feature dimensions automatically

with histograms consisting only of a small number of

peaks, break them up into pseudo-predicates and em-

ploy predicate-based measures directly (i.e. without

quantisation) on them. Our hope is that a DPM kernel

using this approach will come even closer to human

similarity assessment while avoiding the costly pro-

cess of the Greedy algorithm.

The next step will be to apply the DPM to data

from different domains in order to proof its universal-

ity. We are positive that the development of a univer-

sal DPM framework is at reach and will ultimately

lead to improved performance in similarity assess-

ment which provides the basis for classiﬁcation, clus-

tering and information retrieval.

REFERENCES

Chater, N. and Vitnyi, P. M. (2003). The generalized uni-

versal law of generalization. Journal of Mathematical

Psychology, 47:346–369.

Cormen, T. H., Leiserson, C. S., Rivest, R. L., and Stein,

C. (2009). Introduction to Algorithms. Massachusets

Institute of Technology.

Eidenberger, H. (2003). Distance measures for MPEG-

7-based retrieval. In Proceedings of the 5th ACM

SIGMM International Workshop on Multimedia In-

formation Retrieval, MIR ’03, pages 130–137, New

York, NY, USA. ACM.

Eidenberger, H. (2012). Handbook of Multimedia Informa-

tion Retrieval. atpress.

Faloutsos, C. and Lin, K.-I. (1995). Fastmap: A fast algo-

rithm for indexing, data-mining and visualization of

traditional and multimedia datasets. In Proceedings of

the 1995 ACM SIGMOD International Conference on

Management of Data, SIGMOD ’95, pages 163–174,

New York, NY, USA. ACM.

Milgram, J., Cheriet, M., and Sabourin, R. (2006). ”One

Against One” or ”One Against All”: Which One

is Better for Handwriting Recognition with SVMs?

In Lorette, G., editor, Tenth International Work-

shop on Frontiers in Handwriting Recognition, La

Baule (France). Universit

e de Rennes 1, Suvisoft.

http://www.suvisoft.com.

Salton, G., Wong, A., and Yang, C. S. (1975). A vector

space model for automatic indexing. Commun. ACM,

18(11):613–620.

Santini, S. and Jain, R. (1999). Similarity measures. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 21/9:871–883.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

146

Shepard, R. N. (1987). Toward a universal law of

generalization for psychological science. Science,

237/4820:1317–1323.

Tenenbaum, J. B. and Grifﬁths, T. L. (2001). Generaliza-

tion, similarity, and bayesian interference. Behavioral

an, 24:629–640.

Torgerson, W. S. (1952). Multidimensional scaling: I. the-

ory and method. Psychometrika, 17/4:401–419.

Tversky, A. (1977). Features of similarity. Psychological

Review, 84 (4):327–352.

Wisniewski, E. J. and Bassok, M. (1999). What makes

a man similar to a tie? stimulus compatibility with

comparison and integration. Cognitive Psychology,

39(34):208 – 238.

Yang, Y. and Liu, X. (1999). A re-examination of text

categorization methods. In Proceedings of the 22Nd

Annual International ACM SIGIR Conference on Re-

search and Development in Information Retrieval, SI-

GIR ’99, pages 42–49, New York, NY, USA. ACM.

Similarity Assessment as a Dual Process Model of Counting and Measuring

147