Summary Processing of Radiophysical Complex MRTHR Signals
Multifractal Analisys of the Brain Microwave Radiation and Heart Rate Variability
Vladimir Kublanov, Vasilii Borisov and Anton Dolganov
Research Medical and Biological Engineering Centre of High Technologies, Ural Federal University,
Mira 19, 620002, Yekaterinburg, Russian Federation
Keywords: Multifractal Fluctuations Analysis, Multifractal Cross-Correlation Analysis, Brain Microwave Radiation,
Heart Rate Variability.
Abstract: The principles of processing signals of Radiophysical complex MRTHR for studying the role of autonomic
regulation in the formation of the brain microwave radiation during the treatment process are presented. The
feature of this complex is the possibility of registration and analysing the non-stationary short-term time series
of the brain microwave radiation and heart rate variability signals. The processing is implemented via the
method of multifractal cross-correlation analysis. The results of the fluctuation and cross-correlation Hurst
exponent estimations of these signals are shown. The estimates for a group of relatively healthy patients have
low levels of systemic discrepancy. For the patients group with ischemic stroke before treatment the
systematic discrepancy of estimations are significantly larger than those of healthy patients. After
rehabilitation course, the discrepancy between these estimates are reduced.
1 INTRODUCTION
Human brain is among the most complex biological
system. Several interconnected systems take part in
organization of the human brain functioning: neural
networks, glia, cerebral velum, system of
cerebrospinal fluid circulation, and the blood
circulation system. Each of these systems are
complex multiparametric biophysical structure with
cross-interconnections. Is a between all mentioned
systems the blood circulation system takes special
place. This system is controlled by neurogenic,
humoral, metabolic, and myogenic regulatory loops
(Moskalenko, 1992).
Human brain functioning, behaviour and it’s
cognitive activity have abundance of features. The
number of methods for diagnosis and identification of
the information patterns formed by the various
regulatory systems of the organism is also
inexhaustible.
In present article, the brain microwave radiation is
the object of the study. From the physical point of
view, the brain emits radiation caused by the
Brownian motion of micro-charges and microscopic
currents (Rytov et al., 1989). In 80’s of the last
century, academician Y.V. Gulyaev and E.E. Godik
formulated the hypothesis of parametric modulation
of own physical fields of human by biochemical and
biophysical processes in the organism (Godik and
Gulyaev, 1991). The results of our experimental
studies of the fluctuations of the brain microwave
radiation confirm correctness of this hypothesis
(Syskov et al., 2012; Kublanov, 2013). In these
studies, the statistical methods and information
analysis were applied.
One might ask: why obtaining knowledge about
role of the autonomic regulation in the brain
microwave radiation formation is important and
relevant problem? Firstly, it is explained by the fact
that suprasegmental departments of the autonomic
nervous system (ANS) are involved in the regulation
of the cerebral blood flow and cognitive processes
(Guyton and Hall, 2011).
However, given the complexity of the regulatory
systems that form studied biomedical signals, results
obtained via statistical methods and information
analysis do not completely and objectively reflect
characteristics of these dynamic and autonomic
processes.
Moreover, it is well known that biological systems
are capable for self-organization. Self-organization is
the process of spontaneous formation and
development of complex regular structures. This does
not contradict the thermodynamics laws as all living
Kublanov, V., Borisov, V. and Dolganov, A.
Summary Processing of Radiophysical Complex MRTHR Signals - Multifractal Analisys of the Brain Microwave Radiation and Heart Rate Variability.
DOI: 10.5220/0005658101430149
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 143-149
ISBN: 978-989-758-170-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
143

biological systems are not reserved and exchange
energy with environment. Therefore, it is perspective
to use methods of nonlinear analysis (Haken, 1996;
Başar and Güntekin, 2007).
The subjects of analysis in this article are
biomedical signals recorded by the Radiophysical
complex MRTHR. This complex allows one to
simultaneously record time series of the microwave
radiation in the left and right parietal areas of the
brain, and the electrocardiogram of the first limb lead.
The heart rate variability (HRV) signals are
consequently derived from electrocardiogram time
series. The complex consist of the dual-channel
microwave radiometer MRT-40, which is used for
registration of the brightness temperature of deep
structures of the brain, and the electrocardiogram
recorder (Kublanov, 2013).
In (Ushakov and Bogomolov, 2014) it was shown
that to improve the quality of identification of
physiological patterns of biomedical signals, one
must use appropriate mathematical methods for
condition diagnosis. These methods include the
diagnosis of conditions that describe the
characteristics of the series methodology of diagnosis
the risk of violating the state, methodology for
synthesis of the integrated indicators and indexes of
status.
Various biomedical signals reflect different
physiological processes. As the connection between
the ANS and formation of the brain microwave
radiation is evident one might find their correlation in
similar time windows of corresponding biomedical
signals. We propose to use methods of multifractal
formalism for evaluation of the information
characteristics for signals of the brain microwave
radiation and the HRV. Simultaneous registration and
analysis of these signals give new opportunities that
allow one to define a new integral indicator for the
study of functional changes in the brain. This
information can be obtained when the brain studies is
in a state of preclinical and clinical practice in the
early stages of development of these changes.
In (Kublanov et al., 2015), results were presented
for simultaneous analysis of signals the brain
microwave radiation and HRV time series (TS).
These results indicate the relationship between
multifractal parameters for group of healthy subjects.
The changes of brain microwave radiation fluctuation
with periods 20–40 seconds are connected with the
changes of HRV in the time-scale boundaries 6.5–25
seconds. In addition, the fluctuations of the brain
microwave radiation with periods 50–70 seconds are
related with the changes of HRV in the boundaries of
25–300 seconds.
The aim of this paper is to apply the multifractal
formalism for evaluation of autonomic regulation role
in the brain microwave radiation formation during
treatment process.
2 MATERIALS AND METODS
To evaluate the role of autonomic regulation the brain
microwave radiation formation, we use the
multifractal formalism estimations. These
estimations are based on the multifractal detrended
fluctuation analysis MFDFA (Kantelhardt, 2011).
To acquire summary estimation of the microwave
radiation of human signals, which indicate the ANS
variability, one must transform the original
biomedical signals to equidistant TS with the same
sampling frequency.
2.1 Multifractal Detrended Fluctuation
Analysis
After interpolation, the investigated TS are divided
into integer number of non-overlapping segments of
equal length s. Argument s is related to the selected
time windows (i.e., time scale boundaries) for
detecting biomedical signals fluctuations and defined
as the uniform logarithmic apportionment between
time windows boundary points.
Then we do the detrending procedure (Peng et al.,
1995). The detrending starts with finding the function
with the most suitable polynomial trend for each
segment v from the TS. After that, the variations are
calculated



(
,
)
=


∑[

(

)
−

(

)]
.



(1)
The variations set for all segments can be
characterized by the fluctuation function with the
degree q in range q=[-5,5]. For nonzero values, the
fluctuation function is defined by the equation (Ihlen,
2013)


(
,
)
={



∑
[


(,)]
/


}
/
.
(2)
For q=0, we solve the following equation:


(
0,
)
=



∑
[


(
,
)
]


.
(3)
The fluctuation function for self-similar TS
depends on the window width s as degree
(Mandelbrot, 2002)

(,)
≈


()
.
(4)
The exponent degree in equation (4) is called the
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
144

generalized Hurst exponent (GHE) and calculated
from the slope of fluctuation function against s in
logarithmic coordinates.
For monofractal signals, the GHE does not depend
on q. For multifractal signals, positive q denotes
behavior of large fluctuations; negative q denotes
behavior of small fluctuations.
In general case, a multifractal set is characterized
by the scaling exponent s(q). The function τ(q) shows
how heterogeneous the selected set is. The GHE is
connected with scaling exponent τ(q) as follows:

(

)
=∗

()− 1.
(5)
The multifractal spectrum width is determined by
the spectral distribution function D using Legendre
transformation as probability distribution of q
(Kantelhardt, 2011).
D
(

)
=∗−,
(6)
where
=


 is the Hölder exponent.
The quantitative measure of the MFDFA is the
Hurst exponent ℎ=|

(Ihlen, 2013).
2.2 Multifractal Cross-Correlation
Analysis
For investigation of cross-correlation between two
TS, the one can use method of the Multifractal cross-
correlation Analysis (MFCCA) (Podobnik and
Stanley, 2008). The cross-correlation function are
defined as followed:



(
,
)
=
1


[
x
(

)
−x

(

)]
∗


∗
[
y
(

)
−
y

(

)]
(7)


(
,
)
={
1
N

[


(,)]
/


}
/
≈
≈s


()
(8)


(
0,
)
=
1
N

lnF


(
,
)



≈
≈


(()
(9)
After that, the Legandre transform is used similar
to equations (5), (6). Finally, the cross-correlation
Hurst exponent is estimated
ℎ

=

|

. The
exponent is used to detect long-term cross-correlation
between two different signals (Krištoufek, 2011).
Usually, the values of the cross-correlation Hurst
exponent are in range [0; 1.5]. The h=0.5 is a critical
value, as it indicates that two investigated TS are not
correlated or that TS are independent on a low scales.
For h>0.5, two TS have cross-persistence. It is
believed that increments of cross-persistent TS have
a trend to keep fluctuation changes w.r.t. each other.
For h<0.5, two TS have cross-anti persistence. Cross-
anti persistent TS have a tendency for
multidirectional trends in specific time window
(Zhou, 2008).
2.3 Program of Research
The collective analysis of the HRV and brain
microwave radiation signals was performed based on
investigations that were conducted in the Sverdlovsk
Clinical Hospital of Mental Diseases for Military
Veterans (Yekaterinburg, Russian Federation).
The investigations were conducted on the
following groups of patients: the first group was 20
neurologically healthy patients volunteers aging 18-
20 years, the second group was 14 patients suffering
from ischemic stroke (prior to the treatment), the third
group was 7 patients from the second group after
treatment processes, for whom the improvement was
clinically proved.
The record of biomedical signals was obtained
with the modernized Radiophysical complex
MRTHR in two functional states of the patients:
functional peace (F) and orthostatic load (O). Length
of the signals in each states is approximately 300
seconds. The record of the brain microwave radiation
(BMR) signals was performed simultaneously in the
left and right parietal hemisphere of the human brain.
At the same time, the HRV signals were registered.
3 DATA ANALYSIS AND
DISCUSSIONS
The described method can be generalized for
detection of long-term multifractal cross-correlation
between two different biomedical signals recorded
simultaneously. The HRV signals are not equidistant
compared to signal of the brain microwave radiation.
So, it is advised to use cubic spline interpolation prior
to the HRV signals investigation (De Boor, 1978;
Kukushkin et al., 2010). For summary multifractal
estimate, evaluation of the HRV and the brain
microwave radiation signals, the interpolation was
implemented with the same sampling frequency equal
to 10 Hz.
The following time windows were used to
investigate the multifractal properties of short-term
biomedical signals: 1–10, 10–20, 20–30, 30–40, 40–
Summary Processing of Radiophysical Complex MRTHR Signals - Multifractal Analisys of the Brain Microwave Radiation and Heart Rate
Variability
145

50, 50–60, 60–70, 70–80, 80–90 and 90–100 seconds.
The lower boundary of time windows is limited by
interpolation noise (below one second). The upper
boundary is defined by the N/3 ratio, where N is the
length of TS (Kantelhardt, 2011).
3.1 Stages of Multifractal Analysis for
Recorded Biomedical Signals
Here, we present stages of the MFDFA and MFCCA
methods application to the HRV and the brain
microwave radiation signals investigation for one
patient volunteer from the first patient group in the
functional state F.
Fig. 1 presents plots of the Hölder exponent: α
x
(q)
for the HRV signal, α
y
(q) for the brain microwave
radiation signal, α
xy
(q) for the collective analysis of
two signals, respectively.
Figure 1: The Hölder exponent plots.
In Fig. 2 we present plots of scaling exponents:
τ
x
(q) – for the HRV signal, τ
y
(q) – for the brain
microwave radiation signal, τ
xy
(q) – for the collective
analysis of two signals, respectively.
Figure 2: The scaling exponent plots.
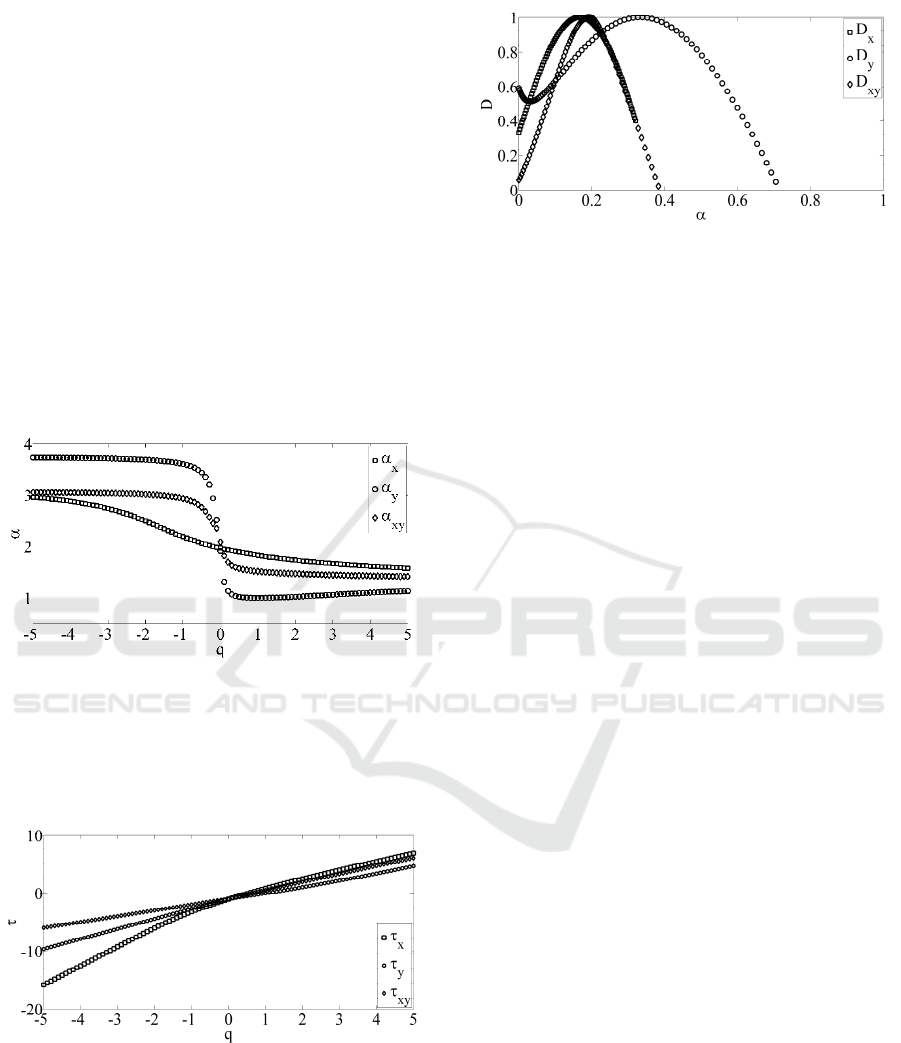
Fig. 3 presents plots of the spectral distribution
functions: D
x
(α) for the HRV signal, D
y
(α) for the
brain microwave radiation signal, D
xy
(α) for the
collective analysis of two signals, respectively.
Figure 3: The multifractal spectrum plots.
3.2 Application of the Bland-Altman
Criterion
Diagnostic possibility of the obtained multifractal
features of selected biomedical time windows for two
functional states was determined by the Bland-
Altman criterion. Firstly, the systematic discrepancy
is counted as difference of each for each pair of
exponentsℎ


−ℎ


. After that, the mean
value <∆> and standard deviation σ for the
differences are obtained. The standard deviation
characterizes the scatter degree of results (Bland and
Altman, 1986).
The final estimates of modulus of systematic
discrepancy of the Hurst exponents obtained by the
MFDFA and MFCCA for each time window for three
group of patients are presented in the tables below.
Here, the estimates are shown in bold type that have:
• low level of systematic discrepancy between two
functional states for patients of the first group;
• high level of systematic discrepancy between two
functional states for patients of the second group;
• reduction of this level for patients of the third
group.
3.3 Multifractal Fluctuation Analysis
of the Heart Rate Variability and
Brain Microwave Radiation Signals
The estimates of modulus of systematic discrepancy
obtained via the Bland-Altman criterion for
difference of Hurst exponent ℎ


−ℎ


and
calculated for the HRV signals are shown in Table 1.
According to presented data, for patients in the
first group there are time windows with the minimal
systematic discrepancy: 20–40 and 50–70 seconds.
We noted that the standard deviation σ of results for
the first group of patients is relatively low, compared
to the standard deviation σ of results for the second
and third groups.
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
146

It is known, that fluctuations of very low
frequency component VLF of HRV signal with
periods in range 25–300 seconds is complex and have
either two or three independent components
(Fleishman, 2005). The obtained results are
consistent with these ideas. Therefore, it is advisable
to compute summary analysis of the HRV and brain
microwave radiation signals not in all time windows,
but in those, which have minimal value of systematic
discrepancy.
Table 1: Mean and standard deviation of systematic
discrepancy of Hurst exponent of HRV signals.
Time
windows,
seconds



−


First
group
Second
group
Third
group
<∆> σ <∆> σ <∆> σ
1-10 0.01 0.10 0.04 0.11 0.11 0.28
10-20 0.02 0.07 0.05 0.34 0.07 0.48
20-30
0.01 0.05 0.11 0.13 0.02 0.11
30-40
0.01 0.18 0.13 0.21 0.08 0.15
40-50 0.03 0.10 0.19 0.52 0.16 0.25
50-60
0.03 0.29 0.21 0.44 0.01 0.30
60-70
0.01 0.41 0.14 0.97 0.02 0.52
70-80 0.23 0.67 0.39 0.49 0.02 0.82
80-90 0.02 0.40 0.17 0.85 0.27 0.61
90-100 0.12 0.64 0.39 1.05 0.19 1.41
In Table 2, we present modulus of the estimates of
systematic discrepancy obtained via the Bland-
Altman criterion for difference of the Hurst exponent
ℎ


−ℎ


calculated for signals of the right
channel of the microwave radiothermograph MRT-40
of modernized Radiophysical complex MRTHR.
Table 2: Mean and standard deviation of systematic
diffeerence of Hurst exponent of the brain microwave
radiation signals.
Time
windows,
seconds



−


First
group
Second
group
Third
group
<∆> σ <∆> σ <∆> σ
1-10
0.05 0.07 0.03 0.21 0.01 0.04
10-20
0.03 0.21 0.03 0.17 0.05 0.10
20-30
0.01 0.17 0.13 0.24 0.12 0.13
30-40
0.01 0.23 0.11 0.55 0.05 0.11
40-50
0.08 0.24 0.14 0.45 0.20 0.38
50-60
0.02 0.38 0.28 0.37 0.05 0.32
60-70
0.03 0.45 0.30 0.73 0.16 0.38
70-80
0.25 0.78 0.45 0.87 0.19 0.61
80-90
0.09 0.69 0.76 1.53 0.47 0.67
90-100
0.25 1.33 0.10 0.35 0.75 1.65
For signals of the right channel of the microwave
radiothermograph MRT-40, the mean values <∆> and
standard deviations σ of differences in time windows
20–40 and 50–70 seconds for patients in second
group are higher than those of patients in first group.
For patients in the third group, there is a tendency of
reduction of the mean values <∆> and standard
deviations σ. The signals of the left channel of the
microwave radiothermograph MRT-40 have the same
properties.
In (Borisov and Kublanov, 2015), it was shown
that the lowest discrepancy of the Hurst exponent h
estimations between signals of the right and left
channel of the microwave radiothermograph MRT-40
in functional states F and O for group of relatively
healthy patients is observed for time windows 10–40
and 60–70 seconds. For that time windows, signals
have anti-persistent properties. Fluctuations of the
signal with periods more than 70 seconds have
blended multifractal properties.
In present study, results of estimates of
discrepancy of the Hurst exponent h obtained for
groups with different nosological status do not
contradict to previous results.
In addition, these results are adequate to earlier
investigation of the nature of the brain microwave
radiation in frequency band from 650 to 850 MHz
(Kublanov et al., 2010). In that work, it was shown
that fluctuations of radiation corresponds to different
physical mechanisms
• fluctuations with periods from 6.5 to 40 seconds
reflect dynamics of liquid transport in the
intracellular and intercellular spaces of human
brain tissues;
• fluctuations with periods higher than 40 seconds
mostly reflect the thermodynamic changes in
human brain tissues.
3.4 Summary Estimation of the Heart
Rate Variability and Brain
Microwave Radiation Signals
In this section, we present results of collective
analysis of the HRV signals and fluctuations of the
brain microwave radiation obtained via the
Multifractal cross-correlation analysis.
The estimates of modulus of systematic
discrepancy obtained via the Bland-Altman criterion
for difference of the cross-correlation Hurst exponent



−


and calculated for the HRV
and brain microwave radiation signals between two
functional states are shown in Table 3.
Summary Processing of Radiophysical Complex MRTHR Signals - Multifractal Analisys of the Brain Microwave Radiation and Heart Rate
Variability
147

According to the data presented in Table 3, the
estimates of differences of the cross-correlation Hurst
exponent in time windows 20–40 and 50–70 seconds
for patients in the first group have low level of
systematic discrepancy.
Table 3: Mean and standard deviation of systematic
discrepancy of the cross-correlation Hurst exponent of the
HRV and brain microwave radiation signals.
Time
windows,
seconds



−


First
group
Second
group
Third
group
<∆> σ <∆> σ <∆> σ
1-10
0.04 0.06 0.04 0.18 0.07 0.19
10-20
0.05 0.25 0.03 0.14 0.08 0.25
20-30
0.01 0.15 0.10 0.34 0.03 0.31
30-40
0.01 0.13 0.05 0.34 0.05 0.51
40-50
0.15 0.53 0.12 0.67 0.85 1.07
50-60
0.05 0.18 0.30 1.36 0.20 0.73
60-70
0.01 0.32 0.10 1.54 0.05 0.83
70-80
0.12 1.92 1.22 3.19 1.00 2.11
80-90
0.32 1.69 1.46 3.18 0.55 2.52
90-100
0.17 3.82 1.05 1.81 0.01 1.71
In Table 4, we present modulus of the estimates of
systematic discrepancy obtained via the Bland-
Altman criterion for difference of the cross-
correlation Hurst exponent



−


and
calculated for signals of the right channel (RC) and
left channel (LC) of the microwave radiothermograph
MRT-40 of Radiophysical complex MRTHR.
Table 4: Mean and standard deviation of systematic
discrepancy of cross-correlation Hurst exponent of right
and left channels of the microwave radiothermograph
MRT-40.
Time
windows,
seconds



−


First
group
Second
group
Third
group
<∆> σ <∆> σ <∆> σ
1-10
0.03 0.09 0.04 0.15 0.01 0.04
10-20
0,11 0.25 0.04 0.25 0.12 0.15
20-30
0.02 0.15 0.15 0.25 0.03 0.15
30-40
0.02 0.13 0.18 0.36 0.06 0.28
40-50
0.32 1.11 0.35 0.56 0.19 0.81
50-60
0.02 0.20 0.55 0.65 0.13 0.93
60-70
0.28 1.57 0.38 1.34 0.62 2.22
70-80
0.07 3.12 0.43 1.54 1.12 2.09
80-90
0.18 2.24 0.36 1.50 0.22 1.11
90-100
0.58 4.42 0.04 2.07 0.14 2.70
Data presented in Table 4 show that estimates of
difference of the cross-correlation Hurst exponent of
simultaneously recorded right and left channels of the
microwave radiothermograph MRT-40 have low
level of systematic discrepancy in time windows 20–
40 and 50–60 seconds for patients in the first group.
For patients in the second group, the estimates of
difference of the cross-correlation Hurst exponent in
mentioned time windows have higher values
compared to estimates in the first group. The
estimates of difference in time windows 20–40 and
50–60 seconds for patients in the third group have
lower values compared to those in the second group.
These results can be interpreted as the assessment of
the treatment process efficiency for patients with
clinically proved improvement.
It is worthy to note that the minimal level of
systematic discrepancy between signals of the HRV
and brain microwave radiation characterizes the
similarity of dynamic changes in these signals. In this
case, one can conclude that role of the autonomic
regulation defined by the parameters of HRV signal
in the formation of the brain microwave radiation is
high.
4 CONCLUSIONS
The usage of methods of the multifractal fluctuation
and cross-correlation analysis in processing of the
short-term signals of the HRV and brain microwave
radiation allowed one to obtain new knowledge about
the studied biomedical signals.
It was found, that for the time windows 20–40 and
50–60 seconds in the functional rest and during the
passive orthostatic load, the systematic discrepancy
between the differences of the Hurst exponent of
biomedical signals is minimal for the group of healthy
patients. For patients suffering from ischemic stroke
prior to the rehabilitation treatment, these values are
greater. The systematic discrepancy between the
difference of the Hurst exponent of biomedical
signals decreases for patients from this group after
rehabilitation treatment, for whom the improvement
was clinically proved.
Application of the multifractal formalism
demonstrated that the minimal level of systematic
discrepancy of the HRV signals and brain microwave
radiation characterize the similarity of dynamic
changes of these signals. This, in turn, points the high
role of the autonomic regulation in the formation of
the brain microwave radiation. The approach
proposed in the article can be used to monitor the
medical process.
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
148

The processing of biomedical signal by the
multifractal formalism during functional studies
increases the quality of identification of their
physiological patterns and extends capabilities of the
modernized Radiophysical complex MRTHR.
ACKNOWLEDGEMENTS
The work was supported by Act 211 Government of
the Russian Federation, contract № 02.A03.21.0006.
REFERENCES
Başar, E., Güntekin, B., 2007. A breakthrough in
neuroscience needs a "Nebulous Cartesian System".
Oscillations, quantum dynamics and chaos in the brain
and vegetative system. International Journal of
Psychophysiology, 64(1), 108-122.
Bland, J.M., Altman, D.G., 1986. Statistical methods for
assessing agreement between two methods of clinical
measurement. Lancet, 8476(1), 307-310.
Borisov, V.I., Kublanov, V.S., 2015. Features of
multifractal analysis application for estimations of
microwave brain radiation signals. In German-Russian
Conference on Biomedical Engineering, 11, 119-123.
De Boor, C.A., 1978. Practical Guide to Splines. Springer-
Verlag.
Fleishman, A.N., 2005. The IV All-Russian Symposium on
Slow Oscillatory Processes in the Human Body and the
II School/Seminar on Nonlinear Dynamics in
Physiology and Medicine. Human Physiology, 32(2),
248-250.
Godik, E.E., Gulyaev, Y.V., 1991. Functional imaging of
human body. IEEE Engineering in Medicine and
Biology, 10(4), 21–29.
Guyton, A.C., Hall, J.E., 2011. Textbook of medical
physiology. Saunders Elsevier.
Haken, H., 1996. Principles of Brain Functioning: A
Synergetic Approach to Brain Activity, Behavior and
Cognition. Springer.
Ihlen, A.F., 2013. Multifractal analyses of response time
series: A comparative study. Behavior Research
Methods, 45, 928-945.
Kantelhardt, J.W., 2009. Fractal and Multifractal Time
Series, Encyclopedia of Complexity and Systems
Science. Springer-Verlag, 3754-3777.
Krištoufek, L., 2011. Multifractal height cross-correlation
analysis: A new method for analyzing long-range cross-
correlations. Europhysics Letters, 95(6), art. no. 68001.
Kublanov, V.S., Sedelnikov, Ju.E., Azin, A.L., Syskov,
A.M., 2010. The Nature of Fluctuations Own
Electromagnetic Radiation of the Brain. Biomedical
Radioelectronics, 9, 45-54.
Kublanov, V.S., 2013. Microwave radiation as interface to
the brain functional state. Proc. of the International
Conference on Biomedical Electronics and Devices, 6,
318–322.
Kublanov, V.S., Borisov, V.I. , Dolganov, A.Y., 2015. The
interface between the brain microwave radiation and
autonomic nervous system. Annual International IEEE
EMBS Conference on Neural Engineering, 7, 922-925.
Kukushkin, Yu.A., Maistrov, A.I., Bogomolov, A.V., 2010.
Rhythmocardiogram Approximation Methods for
Calculation of Spectral Parameters of Cardiac Rhythm
Variability. Biomedical Engineering, 44(3), 92-103.
Mandelbrot, B.B., 2002. Fractal geometry of Nature (in
Russian). Institute of Computer Science.
Moskalenko, Yu.E., 1992. Cerebral Circulation,
Cardiovascular Diseases(in Russian). Meditsina, vol.1.
Peng, C.K., Havlin, S., Stanley, H.E., Goldberger, A.L.,
1995. Quantification of scaling exponents and
crossover phenomena in nonstationary heartbeat time
series. Chaos, 5, 82–87.
Podobnik, B., Stanley, H.E., 2008. Detrended Cross-
Correlation Analysis: A New Method for Analyzing
Two Nonstationary Time Series. Physical Review
Letters, 100, art. no. 084102.
Rytov, S.M., Kravtsov, Y.A., Tatarskii, V.I., 1989.
Principles of Statistical Radiophysics. Springer, vol. 3.
Syskov, A.M., Borisov, V.I., Parashin, V.B., Kublanov,
V.S., 2012. Information Analysis of Radio Brightness
Temperature Fluctuations in Brain Tissues. Biomedical
Engineering, 46(3), 100-103.
Ushakov, I.B., Bogomolov, A.V., 2014. Informatization of
personalized adaptation medicine programs. Vestnik
Rossiiskoi Akademii Meditsinskikh Nauk, 5(6), 124-
128.
Zhou, W.X., 2008. Multifractal detrended cross-correlation
analysis for two non-stationary signal. Physical
Review.E, 77, art. no. 066211.
Summary Processing of Radiophysical Complex MRTHR Signals - Multifractal Analisys of the Brain Microwave Radiation and Heart Rate
Variability
149