Locally Linear Embedding based on Rank-order Distance

Xili Sun and Yonggang Lu

School of Information Science and Engineering, Lanzhou University, Lanzhou, 730000, China

Keywords: Dimension Reduction, Locally Linear Embedding, Rank-order Distance, Pattern Recognition.

Abstract: Dimension reduction has become an important tool for dealing with high dimensional data. Locally linear

embedding (LLE) is a nonlinear dimension reduction method which can preserve local configurations of

nearest neighbors. However, finding the nearest neighbors requires the definition of a distance measure, which

is a critical step in LLE. In this paper, the Rank-order distance measure is used to substitute the traditional

Euclidean distance measure in order to find better nearest neighbor candidates for preserving local

configurations of the manifolds. The Rank-order distance between the data points is calculated using their

neighbors’ ranking orders, and is shown to be able to improve the clustering of high dimensional data. The

proposed method is called Rank-order based LLE (RLLE). The RLLE method is evaluated by comparing with

the original LLE, ISO-LLE and IED-LLE on two handwritten datasets. It is shown that the effectiveness of a

distance measure in the LLE method is closely related to whether it can be used to find good nearest neighbors.

The experimental results show that the proposed RLLE method can improve the process of dimension

reduction effectively, and C-index is another good candidate for evaluating the dimension reduction results.

1 INTRODUCTION

With the quick development of new services such as

blogs, social networks and location-based services

(LBS), the data type and amount is increasing and

accumulating in amazing speed. The data processing

becomes very complex especially in high

dimensional space, because there are a large number

of superfluous information and certain correlations

hiding among data in high-dimensional space (Zhuo,

2014). Data visualization is also a difficult task for

high-dimensional data. The main goal of dimension

reduction is to transform the high-dimensional data

into a more compact and meaningfully expression in

low-dimensional space, and thus reducing the

computational cost and facilitating the visualization

of the data structure. The lower the dimensionality,

the less is the required space and the processing time.

Dimension reduction is widely used in data

compression, machine learning, pattern recognition,

and data visualization applications (Ding, 2002).

There are two types of dimension reduction:

linear and nonlinear mapping. Linear techniques

suppose that the data lie on or near a linear subspace

of the high-dimensional space, and perform

dimension reduction by linear transformation.

* Corresponding author

Typical linear dimension reduction techniques

include principal component analysis (PCA) (Wold,

1987), linear discriminant analysis (LDA) (Fukunaga,

1990), independent component analysis (ICA)

(Comon, 1992), etc. Nonlinear techniques do not rely

on the linearity assumption and can deal with more

complex data. Compared to linear techniques,

nonlinear techniques for dimension reduction are

more widely used and thus have been studied more

intensively. There are generally two main types of

nonlinear dimension reduction techniques: global

techniques which attempt to preserve global

properties of the original data in the low-dimensional

representation, and local techniques which attempt to

preserve local properties of the original data in the

low-dimensional representation, the literature review

on the research work can be referred to (van der

Maaten, 2009). Typical nonlinear techniques includes

isometric mapping (Isomap) (Tenenbaum, 2000),

local tangent space alignment (LTSA) (Zhang, 2004),

locally linear embedding (LLE) (Roweis, 2000),

Laplacian eigenmaps (LE) (Belkin, 2003), stochastic

neighbor embedding (SNE) (Hinton, 2002), etc.

Isomap and SNE belong to global techniques. Isomap

is a widely used nonlinear dimension reduction

technique, which estimates the intrinsic geometry of

a data manifold based on a rough estimate of each

data point’s neighbors by using geodesic distance on

162

Sun, X. and Lu, Y.

Locally Linear Embedding based on Rank-order Distance.

DOI: 10.5220/0005658601620169

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 162-169

ISBN: 978-989-758-173-1

the manifold. SNE is a stochastic method, which tries

to place the objects in a low-dimensional space so as

to optimally preserve neighborhood identity. LLE, LE

and LTSA are local techniques. LLE preserves local

properties by representing each data point as a local

linear combination of the nearest neighbors. LE

constructs edge-weighted adjacency graphs of

neighbor nodes to preserve local properties. LTSA

uses tangent spaces learned by fitting an affine

subspace in a neighborhood of each data point to

represent the local geometry.

The LLE method has been widely used in many

applications such as image classification, image

recognition, spectra reconstruction and data

visualization, because it is simple to implement and

its optimization does not involve local minima

(Zhang, 2006; Saul, 2003). The main idea of LLE is

to approximate nonlinear structures by gathering of

many linear patches in the high dimensional

manifolds. A patch consists of a data point and its k

nearest neighbors. The correlations between the data

point and its neighbors are mathematically expressed

by a set of n weights which best describe the character

of the local structure within the patch (Varini, 2006).

LLE maps the high dimensional data point to a low

dimensional vector using the n reconstruction weights.

So an important problem in LLE is to find appropriate

neighbors of a data point for defining the linear

patches. In the original LLE method, the neighbors

are identified by using the Euclidean distance

measure, which may cause a data point to have

neighbors that in fact are very distant in the intrinsic

geometry of the data according to the literature

(Varini, 2006). To avoid this problem, several

improvements have been proposed. LLE with

geodesic distance (ISO-LLE) searches for the

neighbors with respect to the geodesic distance

(Varini, 2006). Locally linear embedding based on

image Euclidean distance (IED-LLE) substitutes the

image Euclidean distance for the traditional

Euclidean distance (Zhang, 2007). Weighted locally

linear embedding for dimension reduction (WLLE)

modifies the LLE algorithm based on the weighted

distance measurement to improve dimension

reduction (Pan, 2009). Mahalanobis distance

measurement based locally linear embedding

algorithm (MLLE) utilizes Mahalanobis metric to

choose neighborhoods (Zhang, 2012). Supervised

LLE based on Mahalanobis distance (MSP-LLE)

combines class labeled data and Mahalanobis

distance to choose neighborhoods and use extreme

learning machine to map the unlabeled data to the

feature space (He, 2013).

Different from the methods mentioned above, in

this paper, we have proposed an improved method

based on LLE by using the Rank-order distance (Zhu,

2011) to choose neighborhoods. Rank-order distance

is a newly proposed distance measure, which

measures distance according to the neighborhood

rank information and has been successfully used to

improve the clustering of high dimensional data. The

proposed method has been successfully applied to

two handwritten datasets.

The rest of the paper is organized as follows:

Rank-order distance is described in Section 2; the

proposed RLLE method is introduced in Section 3;

experimental results are presented in Section 4;

finally, the conclusions are given in Section 5.

2 RANK-ORDER DISTANCE

Rank-order distance has been proposed to measure

the similarity according to the neighborhood

information (Zhu, 2011). This method is based on the

consideration that two data points of the same type

usually have similar neighborhood structure, while

the data points of different type usually have

dissimilar neighbors. The Rank-order distance is

computed by three steps:

Step 1. Compute neighbor lists of each data point



using Euclidean distance.

Step 2. Calculate the asymmetric Rank-order

distance D(a,b) between data points a and b by:

()

(,) ( ())

Dab O f i



(1)

where f

(i) is the i-th data point in the neighbor list of

a, O

(b) is the ranking order of b in the neighbor list

of a, and O

(i)) is the ranking order of the data point

(i) in neighbor list of b. It can be seen that D(a,b) is

the sum of the ranking orders of the a’s top neighbors

in the neighbor list of b. The smaller the Rank-order

distance, the more similar neighborhood structure

they have.

Step 3. The final Rank-order distance is

computed by:

(,) (, )

(,)

min( ( ), ( ))

ab Dba

RD a b

ObOa

(2)

The step 3 is to further normalize and symmetrize the

distance calculated in step 2. The normalization is

necessary since D(a,b) is biased towards penalizing

large O

(b), as discussed in (Zhu, 2011).

Locally Linear Embedding based on Rank-order Distance

163

3 THE RLLE METHOD

The LLE method is proposed by Roweis (2000) and

Saul. Locally linear embedding (LLE) is an

unsupervised learning method that attempts to gain a

low-dimensional representation by retaining the local

configuration of patches (a patch is defined as a data

point and its nearest neighbors in high dimensional

space). Although the structure of patches is preserved

by linear fit, the global structure of the data in low

dimensional space is obtained by splicing the patches

together according to the relationship of the high

dimensional data points. So the method can be used

to solve nonlinear dimension reduction problems. In

our RLLE method, the Rank-order distance is used to

find the nearest neighbors instead of the Euclidean

distance.

Suppose that the data comprise of N real-valued

vectors



. The RLLE method can be described as

follows:

Step 1. Find k nearest neighbors of each data

point



using the Rank-order distance defined in

(2) in Section 2.

Step 2. Compute reconstruction weights W

between each data point and its neighbors through

minimizing the reconstruction error which is

measured by the following cost function:

()

iijj

WXWX

=−





(3)

under the constraints



and



is not a part of the k nearest neighbors of



So the weight W

represents the contribution of the j-

th data point to the reconstruction of the i-th data point.

Step 3. The vectors



in low-dimensional

space are computed using the weights computed in

Step 2. The computation is done by minimizing the

reconstruction error in low dimensional space:

()

iijj

YYWY

=−





(4)

under the constraints





and



IYY



, where I is the d×d identity matrix.

The final low dimensional representation of the

data is stored in



4 EXPERIMENTS

4.1 The Datasets

Two real datasets are used in our experiments. They

are scanned images of handwritten digits from the

MNIST (LeCun, 1998) and USPS (Hull, 1994). The

MNIST dataset comprise of 60000 grayscale images

of handwritten digits and every image has 28×28=784

pixels (D=784). In the experiments, 5000 images are

randomly selected as the test samples. The USPS

contains 11000 grayscale images of handwritten

digits with the resolution of 16×16 (D=256). We

randomly choose 5500 images as the test samples.

4.2 Comparison of Four Distances

To evaluate the effectiveness of the Rank-order

distance, it is compared with the Euclidean distance,

image Euclidean distance (IED) as defined in IED-

LLE and geodesic distance as defined in ISO-LLE in

representing local configurations of the manifolds.

They are both used to select k nearest neighbors. Then

for each data point i, the number of the nearest

neighbors which represent the same digit as the data

point is found, and it is denoted as n

. Finally, the

mean of the n

for all the data points are computed.

Table 1 and Table 2 shows the mean of the n

calculated using the Euclidean distance, the Rank-

order distance, the IED distance and the geodesic

distance for MNIST and USPS datasets respectively.

The value of k varies from 4 to 18. It can be seen from

Table 1 and Table 2 that the mean values computed

using the Rank-order distance for different k’s are all

larger than the mean values computed using the

Euclidean distance and the geodesic distance, which

indicates that the Rank-order distance can find better

candidates of the nearest neighbors than the

Euclidean distance and the geodesic distance.

From Table 1, it is found that the mean values

computed using the Rank-order distance are all larger

than the ones computed using the IED distance for the

MNIST dataset. From Table 2, the mean values

computed using the Rank-order distance are all lower

than the IED distance for the USPS dataset. It shows

that, compared to the IED distance, the Rank-order

distance can find better candidates of the nearest

neighbors for the MNIST dataset, but not for the

USPS dataset. The IED distance uses not only the

grey value of the pixels, but also takes into

consideration the spatial relationship of the pixels,

while the Euclidean distance, the geodesic distance

and the Rank-order distance only considers the grey

value of the pixels. The spatial relationship is stronger

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

164

in lower resolution images than in the high resolution

images because the spatial distances between pixels

are smaller in the low resolution images. This may be

why the IED distance can produce better nearest

neighbor candidates than the Rank-order distance in

the USPS dataset which has a lower resolution than

MNIST dataset.

Table 1: The mean of the number of the nearest neighbors

representing the same digit found using the four distance

measures for the MNIST dataset.

k Euclidean Rank-order Geodesic IED

4 3.661 3.6824

3.6606 3.6756

5 4.5476 4.5732

4.5476 4.5616

8 7.1434 7.1904

7.144 7.1672

10 8.8358 8.9048

8.8374 8.8698

18 15.3808 15.5466

15.389 15.4664

Table 2: The mean of the number of the nearest neighbors

representing the same digit found using the four distance

measures for the USPS dataset.

k Euclidean Rank-order Geodesic IED

4 3.6535 3.7304 3.654 3.7773

5 4.5416 4.6327 4.5427 4.7029

8 7.1195 7.2944 7.1218 7.4245

10 8.8085 9.0325 8.8122 9.2084

18 15.2671 15.7378 15.274 16.1193

4.3 Evaluation of the RLLE Method

For evaluating the effectiveness of the proposed

RLLE method, it is compared with the original LLE

method, the IED-LLE (Zhang, 2007) method and the

ISO-LLE method. In Zhang’s study (Zhang, 2012),

IED-LLE has the best experiment results in USPS

dataset compared with MLLE, LLE. This is why the

IED-LLE method is also selected for comparison. All

the three methods are implemented in Matlab.

Error-rate is usually used as an evaluation

indicator for dimension reduction, and it is obtained

by applying the K-Nearest Neighbor (K-NN)

clustering method on the low dimensional

representation of the dataset, and then computing the

error rate of the clustering results (Saul, 2003).

In our experiments, C-index (Hubert, 1976) is

also selected as an evaluation indicator, which can be

used to evaluate the dimension reduction results

without using any clustering methods. The data in the

low dimensional space are evaluated directly by the

C-index to show the quality of the dimension

reduction using the benchmark labels as the clustering

labels. C-index is given by

min

max min

()

() ()

in in

WWN

Cindex

WN WN

−

(5)

where N

means the total number of intra-cluster

edges, W

min

) denotes the sum of the smallest N

distances in the proximity matrix W computed in the

low dimensional space, W

max

) denotes the sum of

the largest N

distances in the proximity matrix W,

and W

is the sum of all the intra-cluster distances.

The C-index measures to what extent the dimension

reduction puts together the N

point pairs that are the

closest across the clusters given by the benchmark

labels. It lies in the range of [0, 1]. Usually the smaller

the C-index, the better the clustering results is.

There are two parameters in our experiments:

one is the number of the nearest neighbors k, the other

is the reduced number of features d. Using the method

introduced in Kouropteva’s paper (Kouropteva, 2002),

the optimal values computed for k are 5 and 8 for the

MNIST dataset and the USPS dataset respectively.

Besides the optimal k value, the other three k values

used in our experiments are: 4, 10 and 18. For the

other parameter d, the integer values from 2 through

18 are all used in the experiments.

4.4 Experimental Results

Figure 1 shows the change of the error-rate produced

by RLLE, ISO-LLE and IED-LLE compared to the

error-rate produced by LLE for the MNIST dataset

when k=4, k=5, k=10 and k=18. In Figure 1, ∆error-

rate denotes the error-rate of RLLE, ISO-LLE or IED-

LLE minus the error-rate of LLE. When the ∆error-

rate produced by a method is less than zero, it means

that the method produces better results than the LLE

method. It can be seen from Figure 1 that when k=4

the ∆error-rates produced by RLLE are all less than

zero except when the reduced number of features d=2,

and the ∆error-rates of IED-LLE are all larger than

zero except that d is within 2 to 4. When k=5, the

∆error-rates produced by RLLE are all less than zero

except that d is within 2 to 4, and the ∆error-rates

produced by IED-LLE are all larger than zero. When

k=10, the ∆error-rates produced by RLLE are all less

than zero except that d is within 13 to 18, and the

∆error-rates produced by IED-LLE are all larger than

zero except that d is within 2 to 6. When k=18, the

∆error-rates produced by RLLE are all less than zero,

and the ∆error-rate produced by IED-LLE are all less

Locally Linear Embedding based on Rank-order Distance

165

than zero except that the reduced dimension d is

among 14 to 18. For k=4, k=5, k=10 and k=18, the

∆error-rates of ISO-LLE are all close to zero. It can

be seen that the proposed RLLE method can produce

the lowest error-rate in most cases for the MNIST

dataset.

Figure 2 shows the change of the C-index

produced by RLLE, ISO-LLE and IED-LLE

compared to the C-index produced by LLE for the

MNIST dataset. In Figure 2, ∆C-index denotes the C-

index of RLLE, ISO-LLE or IED-LLE minus the C-

index of LLE. Similar to the ∆error-rate, when the

∆C-index produced by a method is less than zero, it

means that the method produces better results than the

LLE method. It can be seen from Figure 2 that when

k=4 the ∆C-indices produced by RLLE are all less

than zero except when d is 2, 10 or 12, and the ∆C-

indices produced by IED-LLE are all larger than zero

except d is within 14 to 18. When k=5 and k=10, the

∆C-indices produced by RLLE are all less than zero

except a special case (k=5, d=2), and the ∆C-indices

of IED-LLE are all less than zero except the cases:

(k=5, d=2 to 12), (k=10, d=2). When k=18, the ∆C-

indices of RLLE are all less than zero except that d is

within 16 to 18, and the ∆C-indices of IED-LLE are

all larger than zero except that d is within 2 to 5. For

k=4, k=5, k=10 and k

=18, the ∆C-indices of ISO-LLE

are also close to zero. So evaluated by the C- index,

RLLE can also produce better results compared to

LLE, ISO-LLE and IED-LLE on MNIST dataset.

Figure 3 shows the change of the error-rate

produced by RLLE, ISO-LLE and IED-LLE

compared to the error-rate produced by LLE for the

USPS dataset when k=4, k=8, k=10 and k=18. It can

be seen that for different values of k the ∆error-rates

produced by RLLE and IED-LLE are all less than

zero except a special case: (k=4, d=3). So for most

cases, the RLLE method can produce better results

Figure 1: ∆error-rate for the MNIST dataset.

Figure 2: ∆C-index for the MNIST dataset.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

166

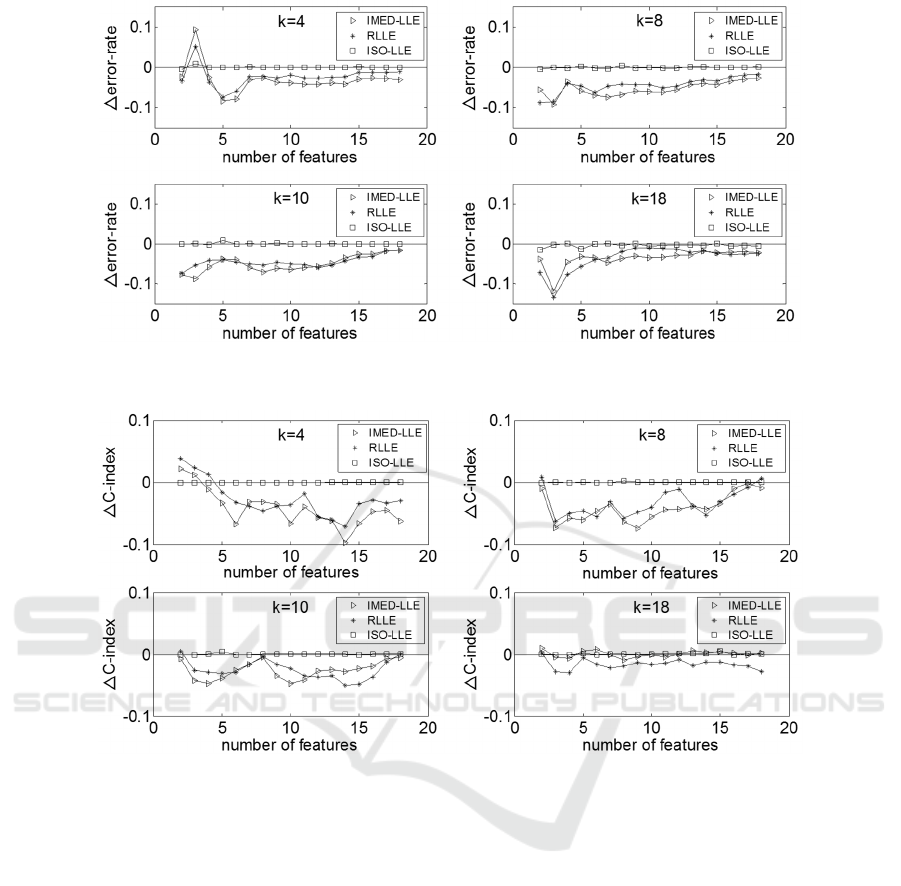
Figure 3: ∆error-rate for the USPS dataset.

Figure 4: ∆C-index for the USPS dataset.

than LLE. It is also noted that most of the ∆error-rates

produced by RLLE are larger than that produced by

the IED-LLE method. For k=4, k=8, k=10 and k=18,

the ∆error-rates of ISO-LLE are all close to zero. It

can be seen that the RLLE method can produce

smaller error-rates than LLE and ISO-LLE, but the

error-rates produced by RLLE are larger than IED-

LLE.

Figure 4 shows the change of the C-index

produced by RLLE, ISO-LLE and IED-LLE

compared to the C-index produced by LLE for the

USPS dataset. It can be seen in Figure 4 that when

k=4 the ∆C-indices of RLLE and IED-LLE are all less

than zero except that d is within 2 to 3. When k=8,

k=10 and k=18, the ∆C-indices produced by RLLE

are all less than zero except in some special cases

when the reduced dimension d is 2 or 18. When k=8

and k=10, the ∆C-indices produced by IED-LLE are

all less than zero. When k=18, the ∆C-indices of IED-

LLE are all close to zero. The ∆C-indices produced

by RLLE are larger than IED-LLE in most cases

when k=4, k=8 and k=10, and the ∆C-indices

produced by RLLE are all less than the IED-LLE

method when k=18. For k=4, k=8, k=10 and k=18, the

∆C-indices of ISO-LLE are all close to zero. It can be

seen that for most cases RLLE method can produce

better C-indices than LLE and ISO-LLE, and IED-

LLE can produce better C-indices than RLLE, which

is consistent with the results measured using error-

rate.

4.5 Discussion

In summary, for the MNIST dataset, the RLLE

method can produce the best results than LLE, ISO-

LLE and IED-LLE. For the USPS dataset, RLLE can

still produce better results than LLE and ISO-LLE in

Locally Linear Embedding based on Rank-order Distance

167

most cases. Although IED-LLE can produce better

results than RLLE when k=4, k=8 and k=10, the

results of RLLE are usually better than these of IED-

LLE when k=18.

It can be seen from Table 1 to Table 2 and from

Figure 1 to Figure 4 that if a distance measure can

find good nearest neighbor candidates, it can also

produce good dimension reduction results combined

with the LLE method. It can also be seen from the

experimental results that using C-index can produce

consistent evaluation results as using the error-rate.

One of the benefits of using C-index is that no

clustering process is needed after the dimension

reduction, which may avoid the bias of the selected

clustering algorithm in the evaluation of the

dimension reduction results.

5 CONCLUSIONS

In this work, we use the Rank-order distance instead

of the traditional Euclidean distance to find the

nearest neighbors and then produce low-dimensional

representation using a similar process as in LLE. It is

shown that the proposed RLLE method can realize

dimension reduction more effectively on the two

image datasets compared to LLE and ISO-LLE, while

producing competitive results compared to IED-LLE.

It is also shown that the Rank-order distance can find

better neighbors than the Euclidean distance and the

geodesic distance for representing local

configurations of the manifolds. The experimental

results also show that C-index is another good

indicator for evaluating the dimension reduction

results. Our future work will focus on reducing the

time complexity in the computation of the Rank-order

distance.

ACKNOWLEDGEMENT

This work is supported by the National Natural

Science Foundation of China (Grants No. 61272213).

REFERENCES

Belkin, M. & Niyogi, P., (2003) Laplacian eigenmaps for

dimensionality reduction and data representation,

Neural computation, 15 (6), 1373-1396.

Comon, P., (1992). Independent component analysis,

Higher-Order Statistics, 29-38.

Ding, C., He, X, & Zha, H. et al., (2002). Adaptive

dimension reduction for clustering high dimensional

data. Proceeding of the 2002 IEEE International

Conference on Data Mining, pp. 147-154.

Fukunaga, K., (1990). Introduction to statistical pattern

recognition, Academic press.

He, L.M., Jin, W. & Yang, X.B. et al., (2013). An algorithm

research of supervised LLE based on mahalanobis

distance and extreme learning machine. In: Consumer

Electronics, Communications and Networks (CECNet),

2013 3rd International Conference on. IEEE, pp. 76-

79.

Hinton, G. E. & Roweis, S.T., (2002). Stochastic neighbor

embedding. In: Advances in neural information

processing systems. pp. 833-840.

Hubert, L. & Schultz, J., (1976). Quadratic assignment as a

general data analysis strategy, British Journal of

Mathematical and Statistical Psychology, 29 (2), 190-

241.

Hull, J. J., (1994). A database for handwritten text

recognition research, IEEE Transactions on Pattern

Analysis and Machine Intelligence, 16 (5), 550-554.

Kouropteva, O., Okun, O. & Pietikäinen, M., (2002).

Selection of the optimal parameter value for the locally

linear embedding algorithm, Proc. 1st Int. Conf. Fuzzy

Syst. Knowl. Discov., pp. 359 -363.

LeCun, Y., Bottou, L. & Bengio, Y. et al., (1998) Gradient-

based learning applied to document recognition.

Proceedings of the IEEE, 86 (11), 2278-2324.

Pan, Y. & Ge, S.S., (2009). A. Al Mamun, Weighted locally

linear embedding for dimension reduction, Pattern

Recognition, 42 (5), 798-811.

Roweis, S.T. & Saul, L.K., (2000) Nonlinear

dimensionality reduction by locally linear embedding,

Science, 290 (5500), 2323-2326.

Saul, L.K. & Roweis, S.T., (2003). Think globally, fit

locally: unsupervised learning of low dimensional

manifolds, The Journal of Machine Learning Research,

4, 119-155.

Tenenbaum, B. et al., (2000). A global geometric

framework for nonlinear dimensionality reduction,

Science, 290 (5500), 2319-2323.

van der Maaten, J.P.L., Postma, E.O. & van den Herik, H.J.,

(2009). Dimensionality reduction: A comparative

review, Tilburg Univ., Tilburg, The Netherlands, Tech.

Rep. TiCC-TR 2009-005.

Varini, C. A., (2006). Degenhard, T.W. Nattkemper,

ISOLLE: LLE with geodesic distance,

Neurocomputing, 69 (13), 1768-1771.

Wold, S., Esbensen, K. & Geladi, P., (1987). Principal

component analysis, Chemometrics and intelligent

laboratory systems, 2 (1), 37-52.

Zhang, L. & Wang, N., (2007). Locally linear embedding

based on image Euclidean distance. In: Automation and

Logistics, 2007 IEEE International Conference on.

IEEE, pp. 1914-1918.

Zhang, X.F. & Huang, S.B., (2012). Mahalanobis Distance

Measurement Based Locally Linear Embedding

Algorithm, Pattern Recognition and Artificial

Intelligence, 25, pp. 318-324.

Zhang, Z. & Wang, J., (2006). MLLE: Modified locally

linear embedding using multiple weights. In: Advances

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

168

in Neural Information Processing Systems, pp. 1593-

1600.

Zhang, Z. & Zha, H., (2004). Principal manifolds and

nonlinear dimensionality reduction via tangent space

alignment, Journal of Shanghai University (English

Edition), 8 (4), 406-424.

Zhu, C., Wen, F. & Sun, J., (2011). A rank-order distance

based clustering algorithm for face tagging. In:

Computer Vision and Pattern Recognition (CVPR),

2011 IEEE Conference on. IEEE, pp. 481-488.

Zhuo, L., Cheng, B. & Zhang, J., (2014). A Comparative

study of dimensionality reduction methods for large-

scale image retrieval, Neurocomputing, 141, 202-210.

Locally Linear Embedding based on Rank-order Distance

169