
Sheduling Mobil Medical Units for Home-healthcare Service
Ciro Alberto Amaya and John Alexander Espitia
Department of Industrial Engineering, University of Los Andes, Kr 1E 19A 40, Bogotá, Colombia
Keywords: Home-healthcare Service, Shift Scheduling, Localization, Mathematical Model, Iterative Solution.
Abstract: This paper addresses a shift-scheduling and localization problem of medical staff for home-healthcare
services. In this problem a private company has to decide where to locate its mobile units and its operational
times. Locations and schedules define the system capacity to attend patients, capacity produces acceptable
service level but operational costs, in contrast, a capacity overestimation requires subcontracting services and
consequently a decrease in expected profit. In this talk we present the situation studied and a mathematical
approach to deal with. The method was used in a real situation improving net profit and increased the expected
served demand.
1 INTRODUCTION
Home-healthcare service allows patients to be treated
in the comfort of their own homes as long as their
situation does not warrant attending a specialized
emergency center. Given the complexity of decisions
about organizing the scheduling of shifts and
deployment of vehicles for a home care emergency
service, on the one hand, and the importance of cost-
benefit factors, on the other hand, in many cases
empirical solutions or ones based on unverifiable
assumptions do not provide a good approach and may
lead to high losses for any business.
Health care providers are broadly classified into
public and private sector. Due to the competitiveness
of the private sector, made up of a large number of
home- healthcare providers, such companies face the
challenge of increasing their coverage and the quality
of their services and simultaneously controlling
excessive costs, that is, they need to ensure that they
meet an increasing demand and boost their profits. To
achieve that, they must find an ideal trade-off
between per-patient income and the per-patient cost
of the treatments and for the latter, take into account
the availability of vehicles, scheduling of shifts and
the number of doctors who attend patients.
Given the competitive nature of a private sector, it
is necessary to count on a specialized staff which is
available to assist its affiliates in their own homes.
When a call for assistance is received, caregivers
must travel to such homes in a vehicle from a
predefined site. If a vehicle within range of the home
is not available, the healthcare provider must rely on
help from an associated company, which amounts to
a failure to meet the demand and results in a loss of
profits. When the available vehicles exceed the
demand, on the other hand, it amounts to an additional
operational cost. Thus, the problem consists of
finding the ideal locations and operational intervals
for both the medical staff and the vehicles, taking into
account:
• Demand distribution changes during the day;
• There is a potential number of sites where
vehicles can be located;
• There is a limited number of vehicles;
• Travel times between potential sites and patient
locations are influenced by the time of day;
• There is a limit on response time: the maximal
time permitted to reach a patient;
• The company has to both meet the demand and
increase profits.
The focus of this paper is on locational and
scheduling decisions made at the tactical level. More
specifically, the aim is to develop and solve a model
to locate qualified resources on a network and
allocate this resources to specific shifts to meet
demand.
This paper is organized as follows. Section 2
provides a summary of the literature on the subject.
Section 3 presents two different mathematical
formulations. Section 4 compares both mathematical
formulations by analyzing some computational
experiments. Finally, last section presents some
100
Amaya, C. and Espitia, J.
Sheduling Mobil Medical Units for Home-healthcare Service.
DOI: 10.5220/0005661301000106
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 100-106
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

conclusions.
2 LITERATURE REVIEW
One of the principal aspects studied here is the
location of vehicles over a network, this situation is
similar to the ambulance location problem. The aim
of ambulance location models is to provide adequate
coverage. In that problem a usual goal is to find the
best locations, fulfilling a certain level of demand,
minimizing the number of ambulances needed.
Models are based on the Location Set Covering
Problem (LSCP) as proposed by Toregas et al.
(1971). The main characteristic of these models are
that demand should be met; therefore it is likely that
infeasibility will arise when no location node ensures
coverage for a demand node. Church & Velle (1974)
presented The Maximal Covering Locating Problem
(MCLP), in which the objective is to maximize the
demand covered by a fixed number of facilities. An
important limitation of previous models is that
coverage is binary, so a zone or demand point is to be
covered in full or is not covered at all.
Previous models guaranties coverage when all
ambulances are available, if different services are
needed, while a vehicle is busy, other vehicles in
other locations can cover that points. In this case,
models with multiple coverage aimed obtaining
several covers for each point of demand. For
example, Church & Gerrard (2003) considered the
multi-level location set-covering model (ML-LSCP)
as a search for the smallest number of facilities
needed to cover each demand a preset number of
times. The models proposed by Gendreau, Laporte, &
Semet (1997) and Karaman (2008) introduced
various service times. Aringhieri et al. (2007)
developed the Lower-Priority Calls Coverage Model
in which they introduced priority for calls and also
took the capacity of facilities into account, as Pirkul
& Schilling (1989) did, but without restricting the
number of vehicles in each location. It is important to
note that they considered the variation in terms of
demand throughout the day and solved the problem
for several intervals in the day.
Another aspect dealt with in previous studies is
the variability of demand and its effect on the location
decisions (Drezner & Wesolowsky, 1991). Most use
the information to relocate locations and thus improve
operations, for example in cases of seasonal
variations in the demand (Ndiaye & Alfares, 2008;
Farahani et al. 2009). Recent studies have shown that
the demand for services can be increased by creating
routes for a fleet in a not fixed-resource environment
(Halper & Raghavan, 2011). The idea of regarding
the demand in terms of points rather than continuous
regions has received some criticism (Yao & Murray,
2013; Franco et al. 2008) but more work needs to be
done on these kinds of formulations to demonstrate
their real benefits, for example, in terms of real
applications and computational complexity.
Nevertheless, in discussing the variability of demand,
our study addresses not only the location but also with
the scheduling of resources, in order to dealing with
dynamic demand patterns.
Taking all of the above into account for the
problem we seek to solve, it becomes evident that the
factor of response time is more flexible in a home-
healthcare service, because, in contrast with the
coverage standard in the ambulance problem, it does
not put the patient´s life at risk. This is an important
difference between the two services, and it led to the
decision to use a deterministic model adding three
new elements: 1. An analysis of profitability and its
relation to the trade-off between meeting the demand
and the resulting costs of doing so. 2. Shift scheduling
in order to avoid relocations. 3. The addition of three
new variables to the problem: served demand, served
demand by coverage, and served demand by capacity.
A source of demand is defined as covered if it is
located within a specified response distance or
response time from a mobile unit, a sum of all sources
of demand covered from a mobile unit is call “served
demand by coverage”. Not necessary all the demand
can be met in a given period of time, because there is
a limit number of vehicles, and also because vehicles
need to travel and attend patients at home. The
amount of demand that vehicles can be met due to
restrictions of capacity (time) is call “served demand
by capacity”. The amount of demand that a vehicle
can met in a period of time depends from both
coverage and capacity, this demand is call “served
demand”.
3 PROBLEM FORMULATION
Let suppose we have a group of demand points, each
has its location and activity during a day. In order to
supply the demand points, we will locate a group of
vehicles and assign a preconfigured shift, within
given locations. A single demand point can be
supplied by a vehicle if the demand point is in the
maximal time permitted to reach it. Vehicles can
work on different shifts and can supply a group of
demand points restricted by the time to reach and
assist them. The problem can be formulated using
next two mathematical formulations:
Sheduling Mobil Medical Units for Home-healthcare Service
101

3.1 Formulation based on Binary
Variables
Let us assume the following notation:
Index and sets
i: index the set of demand points I
j: index the set of location points J
s, k: index the set of shifts S
v,w: index the set of vehicles V
t: index the set of interval times T
Decisional variables
,
: 1 if vehicle is assigned in shift s to location j;
: 1 if node i is covered in the time interval t;
,
: The fraction of demand at point i that is covered
by the vehicles in location in the interval.
Auxiliary Decisional variables
: Expected number of clients (demand) served
during the time interval t;
: Number of vehicles active in the time interval t.
Parameters
L: Number of units of time for a time interval;
: Expected demand at point iduring interval t;
: Limit on the number of vehicles at location j
during time interval t;
∶ Desired response time: maximum time permitted
to travel to a patient;
,
: Expected travel time to demand point i from
location during time interval t;
C
,
: Coverage = 1 if T
,
≤R;
: Expected time for a doctor to examine a patient;
: Revenue for serving one unit of demand;
: Cost of an activated vehicle;
∶ 1 if shift s is available in time interval t;
: 1 if shift s is active in time interval t:
First and last time intervals in a shift are
considered active but unavailable, this time is used by
vehicles to leave and return to depots;
,
: 1 if shift overlaps shift;
: Weighted average travel time at location j during
time interval t =
=
∑
∗
,
∈
∗
,
∑
∈
∗
,
(1)
The problem can be defined by using a graph G =
( U , ) consisting of a set of demand nodes, a set
of location points and as the set of arcs [(.): ∈
, ∈). The objective is to obtain the greatest
possible profit given the revenue from the expected
served demand in each interval:
, and the costs
generated by active vehicles in each interval:
.
These costs include not only the operating expenses
and maintenance of vehicles but also the salaries of
medical staff assigned to them.
The mathematical model is described as:
:
(∑
∈
)
−
(∑
∈
)
(2)
..
∑
∗
,
∗
,
∈
≤
(
∑∑
∗
,
∗
,
)∗
∈
∈
∗
,∀∈,∀
∈
(3)
∑
,
∈
≤1, ∀ ∈,∀∈
(4)
≤
∑
∗
∈
,∀∈
(5)
≤
∑
∑∑
∗
,
∈
∈
∗
∗
,∀∈
∈
(6)
≤
∑∑∑
∗
,
∗
,
∈
∈∈
,∀∈
,∀ ∈
(7)
∑
,
∈
+
∑
,
,
∈
≤ 1,∀ ∈ , ∈
, = +1…
(8)
∑
,
∈
≤1,∀∈,∀∈
(9)
∑∑
,
∈∈
≤
, ∀ ∈ ,∀
∈
(10)
=
∑∑∑
∈∈
∈
,
, ∀ ∈
(11)
,
∈
0,1
∀ ∈ ,
∈
,∈
(12)
∈
0,1
,∀∈,∀∈
(13)
,
∈ [0,1], ∀ ∈ ,∀ ∈ ,∀
∈
(14)
∈
ℝ
,∀∈
(15)
∈ℤ
,∀∈
(16)
Constraint (3) ensures that there are enough
vehicles to meet the demand that is assigned at each
location in the interval. Constraint (4) ensures that
the maximum percentage of satisfied demand in each
demand point i is 100%. Constraints (5) and (6)
determine the actual amount of demand that can be
served, while constraint (5) refers to coverage limits,
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
102

constraint (6) to capacity limits. Constraint (7) is
used to determine which nodes are covered in the
desirable response time. Constraint (8) guarantees
that the shifts assigned to the same vehicle do not
overlap. Constraint (9) ensures that a vehicle is
assigned at most to a single location in an entire shift.
Constraint (10) limits the number of vehicles that can
be accommodated in one location. Constraint (11) is
used to determine the number of vehicles in each
interval. Finally, the variables are defined in (12) to
(16)
3.2 Formulation based on Integer
Variables
The family of constraints (8) and binary
characteristics in the previous model made its
solution very difficult; as is shown in Table 1, we
were able to solve to optimality only a small problem.
So a new approach is proposed, with a formulation
similar to the above except that the variable
,
is
modified by
and constraints (8) and (9) are
removed. The decision now involves the number of
vehicles that should be assigned to the shift at
location j (
).
The formulation does not match specific vehicles
with shifts and also it does not have into account the
maximal number of vehicles than can be used
(implicitly defined by the cardinality of set V in the
Binary Model, section 3.1). So, an additional step is
needed in order to assign different shifts (that not
overlapping) to the same vehicle, this determines the
real number of vehicles needed. To do this, an
assignment model is proposed.
3.2.1 Grouping Method
In the proposed model, the objective is to minimize
the number of groups of vehicles that can be formed.
Let G represents the set of groups and W the set of
vehicles; note that |W| =
∑∑
. Let us define
as the parameter that indicates whether the shift
assigned to vehicle ∈ overlaps the shift assigned
to vehicle ∈ .
The model uses two binary decisional variables:
: 1 if the vehicle is assigned to group ; and
to indicate whether the group is opened or not. It is
presented below
∑
∈
(17)
..
∑
∈
=1, ∀∈
(18)
∑
∈
≤∗
,∀∈
(19)
+
∗
≤1, ∀∈,=
+1…||, ∈
(20)
∈
0,1
, ∀ ∈
(21)
∈
0,1
,∀∈,∈
(22)
Constraint (18) ensures that all vehicles are
assigned to a group. Constraint (19) determines the
opening of a group, a maximal number of shifts
assigned to each vehicle (S) can be used. Constraint
(20) ensures that the same group does not have two
vehicles with overlapping shifts. The variables are
defined in (21) and (22).
4 COMPUTATIONAL RESULTS
To test models, instances were generated by
randomly changing parameters related to the number
of nodes (demand points), locations and the response
time. Table 1 presents the computational results. The
headings in that table are: N: number of demand
nodes, LOC: number of candidate locations, RT:
Response time, OF: objective function obtained by
running both models, IM refers to the integer model
and BM to the binary model; Column DIFF compares
the values of objective function for both models - in
percentages. TIME represents the maximum time in
seconds that the model optimizer ran; for values equal
to 3600 the optimizer finished without finding an
optimal solution. %Served Demand represents the
percentage of served demand returned for both
solution approaches.
Due to the number of variables and constraints
that are required when modeling the problem directly
as a mixed linear integer problem, the Binary Model
is only feasible for small problem instances. We use
the mixed integer solver XPRESS-MP, running on a
computer with an Intel Core i5 processor at 2.53 GHz
and 4 GB of RAM memory.
The results of comparing both models are
presented in Table 1. For both models the solver was
programmed to run for a maximum of one hour. For
those problems taking a time less than 3600 in
Column TIME, the solver was able to find an optimal
solution.
Sheduling Mobil Medical Units for Home-healthcare Service
103
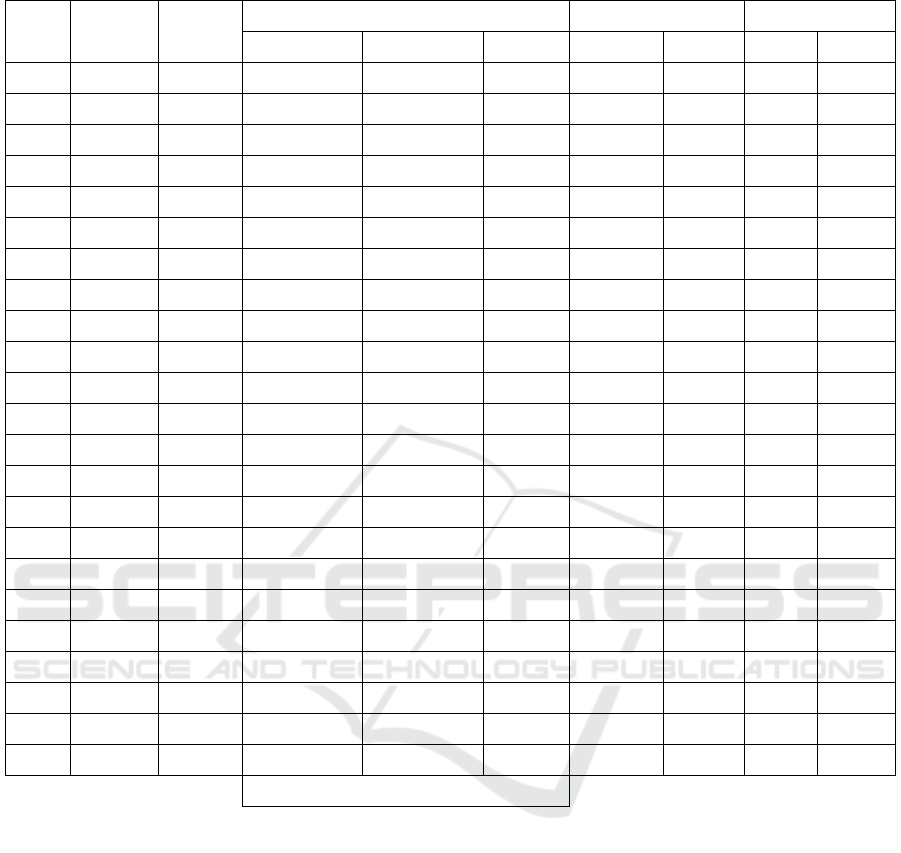
Table 1: Comparison between the integer model (IM) and the binary model (BM).
N LOC
RT
(min)
OF Time (Sec) % Served Demand
IM BM DIFF IM BM IM BM
36 5 5 7,065,880 7,065,880 0% 0.1 4.1 54% 54%
36 5 15 11,313,916 11,313,916 0% 0.5 3,600 96% 96%
36 5 30 10,119,238 10,119,238 0% 0.5 3,600 92% 91%
36 10 5 13,567,621 13,567,621 0% 0.6 3,600 97% 97%
36 10 15 12,307,853 12,307,853 0% 1.0 3,600 97% 96%
36 10 30 11,973,344 11,973,344 0% 0.6 3,600 97% 97%
100 10 10 10,488,912 10,488,912 0% 4.1 3,600 84% 83%
100 10 20 10,023,735 10,023,735 0% 2.2 3,600 97% 94%
100 10 30 8,690,822 8,689,170 0.02% 9.4 3,600 95% 95%
100 20 10 11,717,514 11,716,026 0.01% 299.4 3,600 93% 91%
100 20 20 10,557,368 10,550,887 0.06% 3,600.0 3,600 97% 94%
100 20 30 9,141,004 9,137,759 0.04% 1.9 3,600 95% 94%
196 10 10 6,361,196 6,361,196 0% 1.2 3,600 58% 57%
196 10 20 9,108,291 9,097,342 0.12% 3,600.0 3,600 95% 95%
196 10 30 7,401,324 7,385,140 0.22% 1.4 3,600 97% 92%
196 20 10 10,768,594 10,768,594 0% 5.3 3,600 90% 89%
196 20 20 10,367,695 10,339,842 0.27% 410.3 3,600 97% 94%
196 20 30 8,491,289 8,491,289 0% 2.2 3,600 96% 95%
612 20 20 9,243,522 9,226,088 0.19% 300.5 3,600 96% 95%
612 20 27.5 7,623,919 7,623,919 0% 55.1 3,600 97% 90%
612 20 35 5,864,936 5,864,936 0% 4.1 3,600 94% 90%
1300 20 27.5 7,350,881 7,332,983 0.24% 300.7 3,600 85% 83%
1300 30 27.5 8,620,143 8,580,416 0.46% 1,482.8 3,600 94% 89%
Average DIFF 0.071%
As is shown in the Table 1, the binary model is
more time consuming and in all cases except one was
not able to find optimal solutions in less than an hour.
Insofar as the computational time is concerned, the
results show that for the binary model, the number of
demand nodes and location has a strong influence, the
more demand nodes and locations, the greater the
time needed to solve the problem. By contrast, the
same cannot be established using the integer model.
Finally, the percentage of served demand for the
integer model was always higher than, or at least
equal to, to the result of the binary model.
In order to determine the characteristic of the
solution in relation to the effect of the response time
on the served demand by capacity, coverage and
finally profits, we resolved ten instances in which the
response time (R) varied between 12.5 minutes and
35 minutes and the number of demand nodes and
locations remained constant, with values of 612 and
20 respectively. In these examples the time-lapse for
an interval (L) was 60 (one hour). Figures 1 and 2
show the impact of the response time.
It is interesting to note that for low response times,
the profits are low, and when the response time
increases, so do the profits. The fact that profits begin
to fall at a certain point implies that there is a response
time that maximizes profits. This behavior can be
explained as follows: for lower response times, the
served demand by coverage is small because there are
demand nodes that cannot be reached. By contrast,
the served demand by capacity is high because the
time that it takes to serve a patient is short and so a
higher demand can be served per hour.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
104
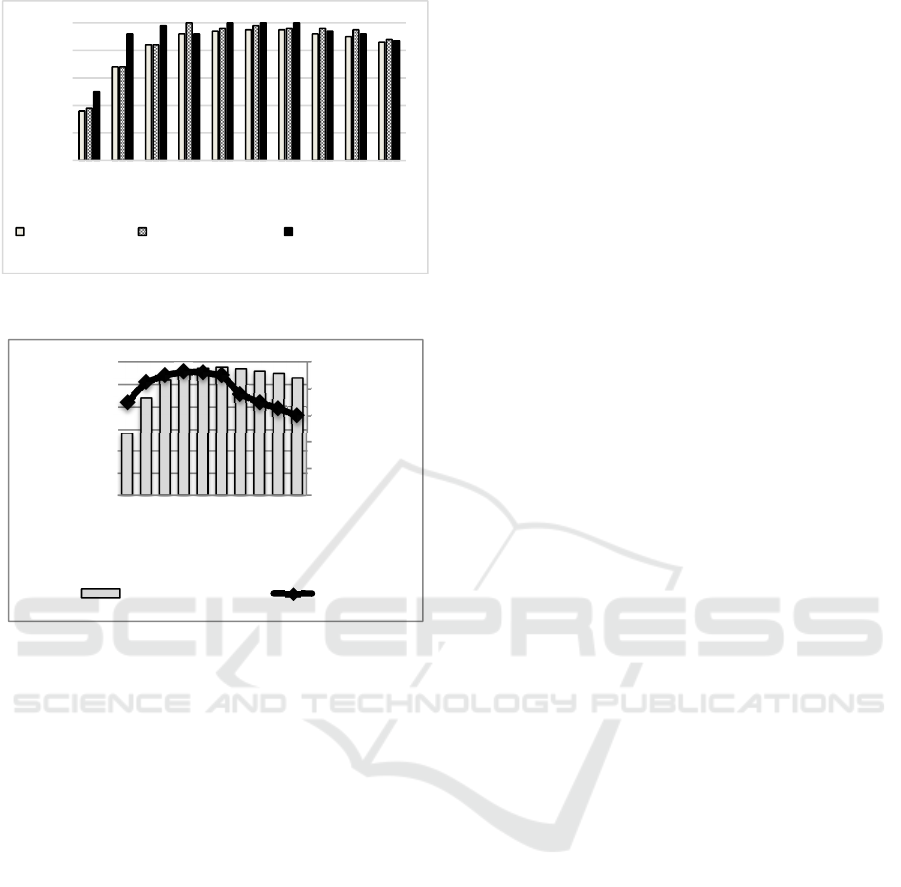
Figure 1: Relation between served demand and profits.
Figure 2: Relation between served demand, served demand
by capacity and served demand by coverage.
On the other hand, when we have higher response
times, the served demand by coverage is high (we can
reach more demand nodes) and the served demand by
capacity is low (we spend more time attending a
patient). In conclusion, for lower response times, we
have low profits because the costs are low but the
revenues are low and also because we cannot cover
so many patients. For higher response times, we have
low profits because the costs related to the number of
vehicles are high.
5 CONCLUSIONS
This study provides some initial practical insights into
the location and shift problem for home-healthcare
services. We employ two mathematical models to
solve the problem. The results of the experiment show
that our Integer model can provide much better
solutions than the Binary model in terms of resolution
time. In future works we want to explore solution
methods for larger instances using open-source
solvers.
In the model we use, profits become an objective
and depend on the number of served patients and the
associated costs of attending those patients, which is
defined by the number of vehicles and shifts used. To
describe and calculate the actual served demand, we
used two variables: served demand by capacity and
served demand by coverage. The former represents
the amount of patients who can be served in relation
to the number of available vehicles and the time
needed to attend to one patient; and the latter
represents the number of patients who can be reached
in the response time. Similarly, we investigated the
influence of the response time on these variables,
concentrating on profits and how it is possible to find
a value for the response time which yields the best
results. For the solution strategy, we propose two
mathematical models but more research is needed to
deal with large problems.
REFERENCES
Aringhieri, R., Carello, G., & Morale, D. (2007).
Ambulance location through optimization and
simulation: the case of Milano urban area. Universita
Degli Studi Di Milano. AIR Archivio Istituzionale Della
Ricerca. Working Paper.
Church, R., & Gerrard, R. (2003). The Multi-level Location
Set Covering Model. Geographical Analysis, 35(4),
277–289.
Church, R., & Velle, C. (1974). The maximal covering
location problem. Papers in Regional Science, 32(1),
101–118.
Drezner, Z., & Wesolowsky, G. O. (1991). Facility location
when demand is time dependent. Naval Research
Logistics (NRL), 38(5), 763–777.
Farahani, R. Z., Drezner, Z., & Asgari, N. (2009). Single
facility location and relocation problem with time
dependent weights and discrete planning horizon.
Annals of Operations Research, 167(1), 353–368.
Franco, C. V., Rodríguez-Chía, A. M., & Miranda, I. E.
(2008). The single facility location problem with
average-distances. Top, 16(1), 164–194.
Gendreau, M., Laporte, G., & Semet, F. (1997). Solving an
ambulance location model by tabu search. Location
Science, 5(2), 75–88.
Halper, R., & Raghavan, S. (2011). The mobile facility
routing problem. Transportation Science, 45(3), 413–
434.
Karaman, M. (2008). A genetic algorithm for the multi-
level maximal covering ambulance location problem.
Master thesis. Middle East Technical University.
Ndiaye, M., & Alfares, H. (2008). Modeling health care
facility location for moving population groups.
Computers & Operations Research, 35(7), 2154–2161.
50%
60%
70%
80%
90%
100%
12,5 15 17,5 20 22,5 25 27,5 30 32,5 35
%Served demand %Deman by coverage %Demand by capacity
$0,00
$2,00
$4,00
$6,00
$8,00
$10,00
40%
50%
60%
70%
80%
90%
100%
12,5 17,5 22,5 27,5 32,5
Profit
% Served Demand
Response Time
%Served demand Profit
Sheduling Mobil Medical Units for Home-healthcare Service
105

Pirkul, H., & Schilling, D. (1989). The capacitated maximal
covering location problem with backup service. Annals
of Operations Research, 18(1), 141–154.
Toregas, C., Swain, R., ReVelle, C., & Bergman, L. (1971).
The Location of Emergency Service Facilities.
Operations Research, 19(6), 1363–1373.
doi:10.1287/opre.19.6.1363.
Yao, J., & Murray, A. T. (2013). Serving regional demand
in facility location. Papers in Regional Science.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
106
