A Variable Neighbourhood Search Algorithm with Compound
Neighbourhoods for VRPTW
Binhui Chen
1
, Rong Qu
1
, Ruibin Bai
2
and Hisao Ishibuchi
3
1
School of Computer Science, The University of Nottingham, Nottingham, U.K.
2
School of Computer Science, University of Nottingham Ningbo, Ningbo, China
3
Department of Computer Science and Intelligent Systems, Graduate School of Engineering,
Osaka Prefecture University, Sakai, Japan
Keywords:
Variable Neighbourhood Search, Vehicle Routing Problem with Time Windows, Compound Neighbourhood,
Metaheuristics.
Abstract:
The Vehicle Routing Problem with Time Windows (VRPTW) consists of constructing least cost routes from a
depot to a set of geographically scattered service points and back to the depot, satisfying service time interval
and capacity constraints. A Variable Neighbourhood Search algorithm with Compound Neighbourhoods is
proposed to solve VRPTW in this paper. A number of independent neighbourhood operators are composed into
compound neighbourhood operators in a new way, to explore wider search area concerning two objectives (to
minimize the number of vehicles and the total travel distance) simultaneously. Promising results are obtained
on benchmark datasets.
1 INTRODUCTION
The Vehicle Routing Problem (VRP) (Laporte, 1992)
is an important transport scheduling problem which
can be used to model various real-life problems, such
as postal deliveries, school bus routing, recycling
routing and so on.
1.1 Problem Description and Related
Work
The Vehicle Routing Problem with Time Windows
(VPRTW) can be defined as follows. Let G = (V, E)
be a directed graph where V = {v
i
, i = 0, . . . , n} de-
notes a depot (v
0
) and n customers (v
i
, i = 1, . . . , n).
A non-negative service demand q
i
and service time s
i
are associated with v
i
, while q
0
= 0 and s
0
= 0. E is a
set of arcs with non-negative weights d
i j
(which often
represents distance) between v
i
and v
j
(v
i
, v
j
∈ V ).
All customer demands are served by a fleet of
K vehicles. To customer v
i
, the service start time
b
i
must be in a time window [e
i
, f
i
], where e
i
and
f
i
are the earliest and latest time to serve q
i
. If a
vehicle arrives at v
i
at time a
i
< e
i
, a waiting time
w
i
= max{0, e
i
− a
i
} is required. Consequently, the
service start time b
i
= max{e
i
, a
i
}. Each vehicle of a
capacity Q travels on a route connecting a subset of
customers starting from v
0
and ending within sched-
ule horizon [e
0
, f
0
]. The decision variable X
k
i j
= 1 if
the arc from v
i
to v
j
is assigned in route k (k ∈ K);
Otherwise X
k
i j
= 0. The objective functions can be de-
fined as follows (Cordeau et al., 2001):
Minimize K (1)
Minimize
∑
k∈K
∑
v
i
∈V
∑
v
j
∈V
X
k
i j
· d
i j
(2)
Subject to:
∑
k∈K
∑
v
j
∈V
X
k
i j
= 1 ∀v
i
∈ V \{v
0
} (3)
∑
k∈K
∑
v
i
∈V
X
k
i j
= 1 ∀v
j
∈ V \{v
0
} (4)
∑
k∈K
∑
v
i
∈V
∑
v
j
∈V \{v
0
}
X
k
i j
= n (5)
∑
v
j
∈V
X
k
0 j
= 1 ∀k ∈ K (6)
∑
v
i
∈V
X
k
i j
−
∑
v
i
∈V
X
k
ji
= 0 ∀k ∈ K, v
j
∈ V \{v
0
}(7)
∑
v
i
∈V
X
k
i0
= 1 ∀k ∈ K (8)
e
i
≤ b
i
≤ f
i
∀v
i
∈ V (9)
Chen, B., Qu, R., Bai, R. and Ishibuchi, H.
A Variable Neighbourhood Search Algorithm with Compound Neighbourhoods for VRPTW.
DOI: 10.5220/0005661800250035
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 25-35
ISBN: 978-989-758-171-7
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
25

∑
v
i
∈V
∑
v
j
∈V
X
k
i j
· q
i
≤ Q ∀k ∈ K (10)
X
k
i j
∈ {0, 1} ∀v
i
, v
j
∈ V, k ∈ K (11)
Objective (1) aims to minimize the requested
number of vehicles. Objective (2) minimizes the total
travel distance of the fleet. Constraints (3)-(5) limit
every customer to be served exactly once and all cus-
tomers are visited. Constraints (6)-(8) define the route
by vehicle k. Constraint (9) and (10) guarantee the
feasibility with respect to the time constraints on ser-
vice demands and capacity constraints (Q) on vehi-
cles, respectively. Constraint (11) defines the domain
of the decision variable X
k
i j
.
Most researchers consider minimizing the number
of vehicles as the primary objective (Br
¨
aysy, 2003),
while others study it as a multi-objective problem
(Ghoseiri and Ghannadpour, 2010). In the former
case, a two-phase approach is often used, to minimize
the vehicle number firstly and then minimize the dis-
tance with a fixed route number in the second phase.
Population-based methods are usually used for solv-
ing the multi-objective VRPTW. Other objectives in
VRPTW include the minimization of the total wait-
ing time and so on, which are less studied (Solomon,
1987; Jozefowiez et al., 2008).
Due to the problem size and NP-hard property of
VRPTW, standard mathematical methods often per-
form poorly within a reasonable amount of time (La-
porte, 1992). Metaheuristics and hybrid algorithms
have attracted more attention in VRPTW. They could
be grouped into population-based metaheuristics and
local search metaheuristics. Population-based meth-
ods work on a set of candidate solutions which re-
quires a high computation cost. This is a main draw-
back for them to achieve high performance in VRP.
More details could be found in (Br
¨
aysy and Gendreau,
2001).
Many local search approaches have been applied
to VRPTW, such as Tabu Search (Potvin et al., 1996),
Simulated Annealing (Van Breedam, 1995) and Vari-
able Neighbourhood Search (VNS) (Hansen et al.,
2010). This paper focuses on VNS methods. Its
first application is on TSP with and without backhaul
(Mladenovi
´
c and Hansen, 1997).
VNS shifts among different neighbourhood struc-
tures which define different search spaces. Different
variants of VNS have been studied in the literature. In
the Basic VNS, a Local Search finds local optimal so-
lutions using different neighbourhood structures, and
Shaking is used to perturb the search to enhance diver-
sification. Variable Neighbourhood Descent (VND)
algorithm changes the neighbourhoods in a determin-
istic way (Hansen and Mladenovi
´
c, 2001). Reduced
VNS (Hansen et al., 2001) selects neighbourhood
moves randomly from a neighbourhood set. General
VNS (Hansen et al., 2006) is an extension of Basic
VNS, whose the local search is a VND as well.
VNS and its extensions have been studied ex-
tensively in various VRP problems. Br
¨
aysy (2003)
proposes a four-phase approach based on VND for
VRPTW. Polacek et al. (2004) develop a VNS for
Multi-Depot Vehicle Routing Problem with Time
Windows where routes start and end at different de-
pots. A VNS algorithm for the Open Vehicle Rout-
ing Problem without time constraint is presented in
(Fleszar et al., 2009). The study in (Hemmelmayr
et al., 2009) concentrates on the Periodic Vehicle
Routing Problem, where the schedule horizon is very
large without time constraint. An extensive review on
VNS can be found in (Hansen et al., 2010).
1.2 Widely Used Neighbourhood
Operators in VRP
Neighbourhood operators define the search spaces of
different features, thus significantly affect the suc-
cess of local search. Neighbourhood moves in VRP
can be classified into two categories: Inter-Route ex-
change and Intra-Route exchange (some authors use
the term interchange instead of exchange), which ex-
change nodes or edges among routes or within one
route, respectively.
Lin (1965) proposes the λ-optimality mechanism,
which is widely applied in routing problems. It re-
moves λ edges from one route, and reconnects it in a
feasible way. 2-opt and 3-opt are two typical opera-
tors of this mechanism, both may reverse the order of
nodes. Or-opt (Or, 1976) is a specific subset of 3-opt
operators, and it includes only those moves which do
not reverse customer links. Osman (1993) introduces
the λ-interchange mechanism which exchanges two
groups of nodes from different routes. The number
of nodes in each group should not be more than λ,
while the nodes are not necessarily consecutive. In
CROSS-exchange (Taillard et al., 1997), two strings
of consecutive nodes from two routes are exchanged,
preserving the order of customers in each string.
The above VNS approaches use independent
moves in each single neighbourhood operator. Er-
gun et al. (2006) combine independent moves such
as 2-opts, swaps and insertions in a very large scale
neighbourhood search. This method is applied to TSP
and VRP with side constraints of capacity and dis-
tance. The independent moves in this method are dif-
ferent on the operation position while their operator
settings are the same. The study shows that this kind
of compounded neighbourhoods are competitive for
solving VRP. This kind of compounding method with
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
26

Figure 1: Examples of neighbourhoods in VNS-C. (a). Link (1,2,3) exchanged with link (5,6) by the intra-route Or-opt-i
compound operator (i=3). (b). Link (2,3,4) exchanged with link (5,6) by the inter-route compound operator CROSS-i (i=3).
(c). Link (4,5) is removed by LinkMove-i from its original route and inserted to a random position in the target route, which
brings a route reduction.
sequential addition and deletion of edges is also used
by Ejection Chain approach (Rego, 1998). In the next
section, we propose and study compound neighbour-
hoods in a different compounding way for VRPTW.
2 VARIABLE NEIGHBOURHOOD
SEARCH WITH COMPOUND
NEIGHBOURHOODS
We propose compound neighbourhood operators into
the General VNS (VNS-C) in this research. In our
approach, compared to existing neighbourhood op-
erators, the independent operators not only are dif-
ferent on the operation position, but also have dif-
ferent lengths of exchange segments. A determinis-
tic constraint is given to exchange segments’ lengths
and a random selection scheme is used to select ex-
change segments. By using this compounding way
in both Intra-Route and Inter-Route neighbourhood
structures, two compound neighbourhoods are pro-
duced. In addition, a third neighbourhood operator
which compounds segment insertion operators with
the same length limit is also developed aiming to re-
duce vehicle number. By adopting these operators,
VNS-C optimizes both objectives simultaneously in
each run by shifting among broader search regions.
2.1 Compound Operators and
Neighbourhoods
Because of the time window constraint in VRPTW,
the reverse operation in the standard λ-opt and λ-
interchange operators tends to bring infeasibility, thus
Or-opt and CROSS-exchange are adopted in the Com-
pound Operators in VNS-C.
Based on the Or-opt exchange operator, we de-
vise an improved Or-opt intra-route operator Or-opt-
i, where i is the length limit of two randomly selected
exchange links. In an Or-opt-i exchange, the length
of one exchange link is fixed to i to avoid redundant
exchanges while the length of the other exchange link
is randomly set to up to i. This exchange link length
setting cooperates with random operation position se-
lection, composing the compounding manner of the
proposed compound neighbourhoods. For example,
Or-opt-3 is a compound neighbourhood which assem-
bles three independent neighbourhood moves (where
one exchange link length is fixed to 3, while the other
one’s length could be 1, 2 or 3). An illustrative exam-
ple is presented in Fig. 1 (a), where directions of both
operated links are kept.
A CROSS-i compound operator is also proposed
in VNS-C. It includes all independent CROSS-
exchanges to exchange a link of length i with another
link of length up to i between routes. For instance,
the compound neighbourhood of CROSS-3 assem-
bles three independent neighbourhood moves where
length of one exchange link is fixed to 3 and the other
A Variable Neighbourhood Search Algorithm with Compound Neighbourhoods for VRPTW
27

one is randomly set to up to 3 (denoted as 3-1, 3-2
and 3-3 independent exchanges, respectively). In one
move of CROSS-3, the best solution among all the
three independent neighbourhoods is selected. While,
in a standard independent neighbourhood search, the
best solution based on only one of the 3-1, 3-2 or 3-3
exchanges will be selected. An example of CROSS-3
is presented in Fig. 1 (b), where the selected improve-
ment solution is produced by a 3-2 exchange.
In the proposed VNS-C, an operator named
LinkMove-i is developed to reduce both the vehicle
number and total travel distance simultaneously (i is
the max length of operated links), rather than in two
separate phases. In LinkMove-i, a customer link of
length α (α ≤ i) from route h is removed and rein-
serted into route t (h 6= t). When α is equal to the
length of route h, route h would be removed thus leads
to a solution with one less route. Fig. 1 (c) presents
an example of LinkMove-i.
The proposed compound neighbourhoods explore
larger search areas than standard independent neigh-
bourhoods. Following the rule of invoking small
neighbourhood moves first, the upper bound i of link
length in compound operators is set to increase from
1 to 5 in VNS-C based on preliminary experiment re-
sults. The order to select the intra-route neighbour-
hood or inter-route neighbourhood first is shown to
be an influence factor in VNS-C in our experimental
results. This is studied in section 3.3.
2.2 Shaking(S)
Shaking(S) is a phase of random perturbation in VNS-
C, which randomly generates a neighbourhood solu-
tion S
0
of the current solution S using the three simple
operators in Table 1, aiming to escape from local op-
tima. ExchangeInRoute-ml and Cross-ml exchanges
two segments within one route and between two ran-
domly selected routes, respectively. Move-ml inserts
a randomly selected route segment from a route to
another route. In all three operators, the maximum
length of the segment is ml. Different from the above-
mentioned compound operators, operators in Shaking
are more flexible, without the requirement that at least
one segment’s length must be ml.
The first feasible move will be accepted in
Shaking(S). To encourage farther moves, the segment
of length ml is selected with a higher probability. If no
feasible moves are found after a pre-specified number
of evaluations, the original input solution S would be
returned. We investigate this process in section 3.2.
Table 1: Set of neighbourhood operators in Shaking. z is a
random variable for selecting an operator. L is the length of
associated routes.
z Operator Min length Max length(ml)
0 ∼ 3 ExchangeInRoute-ml 1 Min(z + 1 , L)
4 ∼ 8 Move-ml 1 Min(z mod 3 , L)
9 ∼ 12 Cross-ml 1 Min(z mod 8 , L)
2.3 Local Search
In the local search of VNS-C (see Algorithm 1),
NS
max
evaluations are undertaken in each run of
neighbourhoods. Hansen et al. (2010) recommend
that, when the initial solution is constructed by a
heuristic, the Best-Improvement acceptance criterion
should be used in VNS. The initial solution in VNS-
C is constructed using the Nearest Neighbourhood
heuristic from (Solomon, 1987), and the best neigh-
bourhood solutions are chosen. To avoid being stuck
to local optima, Record-to-Record Travel algorithm
(Dueck, 1993) is adopted as the acceptance criteria,
where Quality() is defined by the total travel distance,
and DEVIATION is set to 15. Here a solution with
the lower Quality() value is better. The search stops
at a time limit of Time
max
or when all three com-
pound neighbourhoods are estimated. In Algorithm
1, N
r
(S
0
, i) represents the rth neighbourhood opera-
tor applied to the incumbent solution S
0
with operated
link length limit of i.
Algorithm 1: Local Search(S
0
, S).
Step 1: Input solution S
0
and S.
Step 2: Set r ← 1, i ← 1, time ← 0.
while (r < 4 And time < Time
max
) do
Step 2.1: Neighbourhood Search
S
00
← Best Improvement of N
r
(S
0
, i).
time ← time + NS
max
.
Step 2.2: Move or Not
if Quality(S
00
) < Quality(S) then
S ← S
00
, S
0
← S
00
, i ← 0, r ← 1.
else if Quality(S
00
) − Quality(S) <
DEV IAT ION then
S
0
← S
00
, i ← 0, r ← 1.
end if
Step 2.3: Shift Neighbourhood Structure
i ← i + 1.
if i = 6 then r ← r + 1, i ← 1.
end while
Step 3: Output the best found solution S.
2.4 The VNS-C Framework
The pseudo-code of VNS-C is presented in Algorithm
2, where the iteration time is set to C
max
. In Step 1, an
initial solution is constructed using a heuristic, which
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
28

Table 2: Comparison of VNS-C and VNS of Independent Operator with and without Shaking. Best results are in bold.
Instance C101 C201 R101 R201 RC101 RC201
VNS-C
& Shaking
Best
NV 10 3 19 4 15 4
TD 828.94 591.56 1643.34 1190.52 1624.97 1310.44
Average
NV 10 3 19.9 4.83 15.6 4.93
TD 828.94 591.56 1647.9 1246.91 1652.38 1365.76
Times 67,247,717 97,011,547 188,429,463 176,349,146 113,982,405 137,842,632
S.D on NV 0 0 0.31 0.38 0.63 0.25
S.D on TD 0 0 5.59 45.12 12.88 41.57
Independent
Operators
& Shaking
Best
NV 10 3 19 4 16 4
TD 828.94 591.56 1700.42 1339.84 1753.49 1482.86
Average
NV 10 3 20.13 4.73 16.3 4.97
TD 828.94 591.56 1791.73 1538.66 1878.68 1569.51
Times 9,808,756 9,800,000 159,166,298 128,370,863 79,996,218 146,881,580
S.D on NV 0 0 0.68 0.45 0.47 0.18
S.D on TD 4.38 0 89.32 212.51 101.68 59.89
VNS-C
without
Shaking
Best
NV 10 3 19 4 15 4
TD 828.94 591.56 1644.55 1294.36 1644.18 1340.79
Average
NV 10 3 20.43 4.73 16.43 4.93
TD 828.94 591.56 1823.72 1511.68 1856.99 1489.35
Times 10,026,352 97,010,797 77,128,988 124,141,441 104,983,387 113,826,219
S.D on NV 0 0 0.63 0.45 0.68 0.25
S.D on TD 0 0 178.68 394.21 213.67 270.99
Independent
Operators
without
Shaking
Best
NV 10 3 19 4 15 4
TD 828.94 591.56 1649.23 1226.43 1624.97 1332.74
Average
NV 10 3 20.33 4.6 16.17 4.97
TD 828.94 591.56 1828.49 1671.69 1859.35 1443.03
Times 10,198,465 97,066,537 24,214,377 101,344,273 60,738,070 128,573,526
S.D on NV 0 0 0.76 0.5 0.91 0.18
S.D on TD 0 0 173.87 401.52 211.84 199.56
Algorithm 2: The VNS-C framework.
Step 1: Generate an initial feasible solution S by the
Nearest Neighbourhood heuristic.
Step 2:
Set C ← 1.
while C < C
max
do
Step 2.1: S
0
← Shaking(S).
Step 2.2: S ← Local Search(S
0
).
Step 2.3:
if S is improved then
C ← 1.
else
C ← C + 1.
end if
end while
Step 3: Output S.
inserts the ”closest” available customer into the in-
cumbent partial route. Here the distance between two
customers is defined by their Geographic distance d
i j
,
Temporal distance T
i j
and the degree of Emergency
v
i j
which are used in (Solomon, 1987), shown in (12)
as below:
Dis = δ
1
·d
i j
+δ
2
·T
i j
+δ
3
·v
i j
s.t. δ
1
+δ
2
+δ
3
= 1
(12)
The three coefficients δ
1
, δ
2
and δ
3
define the im-
portance of each component in the distance definition.
We set them as δ
1
= 0.4, δ
2
= 0.4 and δ
3
= 0.2 (em-
pirically calculated by Solomon (1987)).
3 EXPERIMENTS
3.1 Problem Dataset and Parameter
Setting
The proposed VNS-C was evaluated on the Solomon
benchmark (Solomon, 1987), which consists of six
datasets (C1, C2, R1, R2, RC1, RC2), each has eight
to 12 instances of 100 customers with their own ser-
vice demands. In C1 and C2, customers are located
in a number of clusters, while the objectives of (1)
and (2) are positively related (Ghoseiri and Ghannad-
pour, 2010). Customers of R1 and R2 are randomly
distributed geographically, while RC1 and RC2 are
a mix of them. The scheduling horizons in C1, R1
and RC1 are short, and their vehicle capacities are low
(200). C2, R2 and RC2 have higher vehicle capacities
(700, 1000 and 1000, respectively), leading to fewer
required vehicles to satisfy all demands. Diverse time
window widths are distributed with various densities.
Tuning is conducted on only one parameter at a
A Variable Neighbourhood Search Algorithm with Compound Neighbourhoods for VRPTW
29

Table 3: T-test between VNS-C and the other three algorithms.
Compared Algorithms C101 C201 R101 R201 RC101 RC201
Independent Neighbourhoods
with Shaking
P-value(NV) 1 1 0.094698 0.355754 1.49E-06 0.561629
P-value(TD) 0.321464 1 1.1E-09 2.3E-08 1.33E-05 6.62E-21
Different N N Y Y Y Y
Compound Neighbourhoods
without Shaking
P-value(NV) 1 1 0.000138 0.355754 0.004581 1
P-value(TD) 1 1 8.66E-06 0.000976 9.92E-06 0.019461
Different N N Y Y Y Y
Independent Neighbourhoods
without Shaking
P-value(NV) 1 1 0.006101 0.046114 5.73E-07 0.561629
P-value(TD) 1 1 3.78E-06 2.74E-06 4.91E-13 0.04599
Different N N Y Y Y Y
Table 4: Results of VNS-C with four different operator orders. Best results are in bold.
Instance C101 C201 R101 R201 RC101 RC201
MCI
Best
NV 10 3 19 4 15 4
TD 828.94 591.56 1643.34 1190.52 1624.97 1310.44
Average
NV 10 3 19.9 4.83 15.6 4.93
TD 828.94 591.56 1647.9 1246.91 1652.38 1365.76
Times 67,247,717 97,011,54 188,429,463 176,349,146 113,982,405 137,842,632
CMI
Best
NV 10 3 20 5 15 5
TD 828.94 591.56 1642.88 1189.82 1623.58 1317.97
Average
NV 10 3 20.3 5 15.87 5
TD 828.94 591.56 1650.42 1214.66 1654.65 1367.59
Times 69,224,764 97,011,573 181,014,272 166,688,866 184,803,844 158,724,815
ICM
Best
NV 10 3 20 4 15 5
TD 828.94 591.56 1642.88 1237.76 1715.49 1354.72
Average
NV 10 3 20.17 4.9 16.4 5
TD 828.94 591.56 1648.9 1306.7 1762.34 1425.46
Times 51,225,270 97,015,461 223,733,841 307,952,033 692,934,814 516,816,576
IMC
Best
NV 10 3 19 4 16 5
TD 828.94 591.56 1643.18 1234.09 1672.33 1376.17
Average
NV 10 3 19.9 4.7 16.27 5
TD 828.94 591.56 1647.52 1334.32 1765 1464.56
Times 67,357,647 97,015,347 199,078,925 311,452,951 735,044,303 492,990,103
time, while fixing all the others on a small number of
instances. Preliminary experiments show that most
feasible solutions in Shaking are found in around
200 evaluations, thus 300 evaluations are conducted.
For each incumbent solution in the local search, 400
neighbourhoods are evaluated, i.e. NS
max
= 400.
Time
max
is set to 1,000,000 evaluations while the max
iteration time C
max
of VNS-C is 300. All results are
produced in 30 runs to conduct statistical analysis.
3.2 Compound Neighbourhoods and
Shaking
Table 2 presents the average results from VNS-C,
VNS with independent operators (standard Or-opt and
CROSS exchange) and VNS-C without Shaking on
six randomly chosen instances. NV denotes the num-
ber of vehicles, TD represents the total travel distance,
and Times is the total number of evaluations. S.D is
the standard deviation. It is shown that VNS-C pro-
duces significantly better and more stable results com-
pared to the other variants. Shaking also improves
VNS-C in terms of both quality and stability, thus is
an essential and necessary component in VNS-C.
To verify whether the result of VNS-C is signif-
icantly different from the other three algorithms’, T-
test is executed between results of VNS-C and the
other three algorithms. Here confidence level is set
as 95%. Table 3 presents the test result, where Y
represents two populations are significantly different,
and N the opposite. Notably, as the solutions have
two dimensions of NV and TD, as long as the p-value
(two-tail) is smaller than 5% in one dimension, the
two populations would be considered as significantly
different. It can be seen that VNS-C produces sig-
nificantly better solutions than the other three algo-
rithms on complicated instances (R and RC). For the
two C instances, there is no significant difference be-
tween VNS-C and the other three algorithms. Results
against those in the literature (see Table 5) indicate
that all these four algorithms obtained the best solu-
tion for these two instances, thus no significant differ-
ence has been found.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
30

Table 5: VNS-C on Benchmark Solomon’s instances. Results that are better than or the same as the best known are in bold.
Instance
Best Known VNS-C
NV TD Ref.
Best Average
NV TD NV TD
C101 10 828.94 (SINTEF, 2015) 10 828.94 10 828.94
C102 10 828.94 (SINTEF, 2015) 10 828.94 10 876.79
C103 10 828.06 (SINTEF, 2015) 10 828.94 10 832.65
C104 10 824.78 (SINTEF, 2015) 10 825.65 10 831.79
C105 10 828.94 (SINTEF, 2015) 10 828.94 10 852.33
C106 10 828.94 (SINTEF, 2015) 10 828.94 10.07 836.25
C107 10 828.94 (SINTEF, 2015) 10 828.94 10 853.9
C108 10 828.94 (SINTEF, 2015) 10 828.94 10 840.48
C109 10 828.94 (SINTEF, 2015) 10 828.94 10 823.94
C201 3 591.56 (SINTEF, 2015) 3 591.56 3 591.56
C202 3 591.56 (SINTEF, 2015) 3 591.56 3.53 613.94
C203 3 591.17 (SINTEF, 2015) 3 591.17 3.07 599.16
C204 3 590.6 (SINTEF, 2015) 3 590.6 3.23 609.81
C205 3 588.88 (SINTEF, 2015) 3 588.88 3 588.88
C206 3 588.49 (SINTEF, 2015) 3 588.49 3 588.49
C207 3 588.29 (SINTEF, 2015) 3 588.29 3 588.29
C208 3 588.32 (SINTEF, 2015) 3 588.32 3 588.32
R101
19 1650.80 (SINTEF, 2015) 19 1652.47
19.9 1647.90
20 1642.87 (Alvarenga et al., 2007) 20 1643.34
R102 17 1486.12 (SINTEF, 2015) 18 1476.06 18.9 1493.30
R103 13 1292.67 (SINTEF, 2015) 14 1219.89 14.17 1230.92
R104
9 1007.31 (SINTEF, 2015)
11.1 1009.910 974.24 (Tan et al., 2006) 10 1007.27
11 971.5 (K
¨
uc¸
¨
uko
˘
g lu and
¨
Ozt
¨
urk, 2014) 11 994.85
R105
14 1377.11 (SINTEF, 2015) 14 1381.88
15.07 1377.24
15 1346.12 (Kallehauge et al., 2006) 15 1360.78
R106
12 1252.03 (SINTEF, 2015)
13.57 1264.04
13 1234.6 (Cook and Rich, 1999) 13 1243.72
R107
10 1104.66 (SINTEF, 2015)
11.73 1097.07
11 1051.84 (Kallehauge et al., 2006) 11 1077.24
R108
9 960.88 (SINTEF, 2015)
10.23 974.46
10 932.1 (Ombuki et al., 2006) 10 956.22
R109
11 1194.73 (SINTEF, 2015)
12.93 1181.9912 1013.2 (Chiang and Russell, 1997) 12 1168.18
13 1151.84 (Alvarenga et al., 2007) 13 1157.61
R110
10 1118.84 (SINTEF, 2015)
12.1 1106.0211 1112.21 (Ombuki et al., 2006)
12 1068 (Cook and Rich, 1999) 12 1081.88
R111 10 1096.72 (SINTEF, 2015) 11 1087.5
11.9 1080.1
12 1048.7 (Cook and Rich, 1999) 12 1062.58
R112
9 982.14 (SINTEF, 2015)
10.9 979.52
10 953.63 (Rochat and Taillard, 1995) 10 958.7
R201
4 1252.37 (SINTEF, 2015) 4 1282.75
4.83 1246.91
5 1206.42 (Tan et al., 2006) 5 1190.52
R202
3 1191.7 (SINTEF, 2015)
4 1146.34
4 1091.21 (Tan et al., 2006) 4 1098.06
R203
3 939.503 (SINTEF, 2015) 3 968.67
3.5 969.05
4 935.04 (Tan et al., 2006) 4 905.72
R204
2 825.52 (SINTEF, 2015)
3 809.88
3 789.72 (Tan et al., 2006) 3 766.91
A Variable Neighbourhood Search Algorithm with Compound Neighbourhoods for VRPTW
31

Table 5: VNS-C on Benchmark Solomon’s instances. Results that are better than or the same as the best known are in bold
(cont.).
(continued)
Instance
Best Known VNS-C
NV TD Ref.
Best Average
NV TD NV TD
R205
3 994.42 (SINTEF, 2015) 3 1059.91
3.83 1029.55
5 954.16 (de Oliveira et al., 2007) 4 964.02
R206 3 906.142 (SINTEF, 2015) 3 931.762 3 994.92
R207
2 890.61 (SINTEF, 2015)
3 896.72
3 814.78 (Rochat and Taillard, 1995) 3 855.37
R208
2 726.82 (SINTEF, 2015) 3 708.9
3 740.94
4 698.88 (Ursani et al., 2011)
R209
3 909.16 (SINTEF, 2015) 3 983.75
3.93 920.18
5 860.11 (Alvarenga et al., 2007) 4 871.63
R210
3 939.37 (SINTEF, 2015) 3 978.11
3.63 992.18
4 935.01
R211
2 885.71 (SINTEF, 2015)
3 828.81
4 761.1 (Ombuki et al., 2006) 3 794.04
RC101
14 1696.94 (SINTEF, 2015)
15.6 1652.38
15 1619.8 (Kohl et al., 1999) 15 1624.97
RC102
12 1554.75 (SINTEF, 2015)
13.97 1497.05613 1470.26 (Tan et al., 2006) 13 1497.43
14 1466.84 (Alvarenga et al., 2007) 14 1467.25
RC103 11 1261.67 (SINTEF, 2015) 11 1265.86 11.8 1284.24
RC104 10 1135.48 (SINTEF, 2015) 10 1136.49 10.7 1171.61
RC105
13 1629.44 (SINTEF, 2015)
15.6 1570.3314 1589.91 (Tan et al., 2006) 14 1642.81
15 1513.7 (Alvarenga et al., 2007) 15 1524.14
RC106
11 1424.73 (SINTEF, 2015) 12 1396.59
13.07 1408.7
13 1371.69 (Tan et al., 2006) 13 1376.99
RC107
11 1230.48 (SINTEF, 2015) 11 1254.68
11.93 1258.32
12 1212.83 (Alvarenga et al., 2007) 12 1233.58
RC108
10 1139.82 (SINTEF, 2015)
11 1149.38
11 1117.53 (Alvarenga et al., 2007) 11 1131.23
RC201
4 1406.94 (SINTEF, 2015) 4 1457.87
4.93 1365.76
6 1134.91 (Tan et al., 2006) 5 1310.44
RC202
3 1365.64 (SINTEF, 2015)
4 1278.96
4 1181.99 (Ombuki et al., 2006) 4 1219.49
RC203
3 1049.62 (SINTEF, 2015)
4 1020.716
4 1026.61 (Tan et al., 2006) 4 957.1
RC204 3 798.46 (SINTEF, 2015) 3 829.13 3 867.85
RC205
4 1297.65 (SINTEF, 2015)
5 1273.03
5 1295.46 (Tan et al., 2006) 5 1233.46
RC206
3 1146.32 (SINTEF, 2015)
4 1152.29
4 1139.55 (Tan et al., 2006) 4 1107.4
RC207
3 1061.14 (SINTEF, 2015)
4 1084.44
4 1079.07 (Rochat and Taillard, 1995) 4 1032.78
RC208 3 828.14 (SINTEF, 2015) 3 830.06 3 922.47
3.3 Neighbourhoods Order
Table 4 compares different orders of neighbourhoods
in VNS-C (M, C and I represent LinkMove-i, CROSS-
i and Or-opt-i, respectively). It can be seen that, the
Inter-Route move first group (MCI and CMI) achieves
better results than the Intra-Route move first ones
(ICM and IMC). In the former case, MCI performs
better than CMI. It seems that optimizing the route
number first, and then assigning customers to a route
and optimizing the customer order in each route can
bring better results. On R101 and R201, MCI obtains
better NV while CMI has better TD. As objective (1)
is usually considered as primary, the order of MCI
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
32

will be used in VNS-C.
3.4 Experiment Results and Analysis
Table 5 presents the results on all the 56 Benchmark
Solomons instances. It illustrates that VNS-C is effec-
tive in improving both objectives simultaneously. In
problems whose objectives are positively correlated,
VNS-C can produce the current best known solutions
in a reasonable time. In other instances, some bet-
ter solutions with less TD are found comparing to the
best known solutions with the same NV in the litera-
ture.
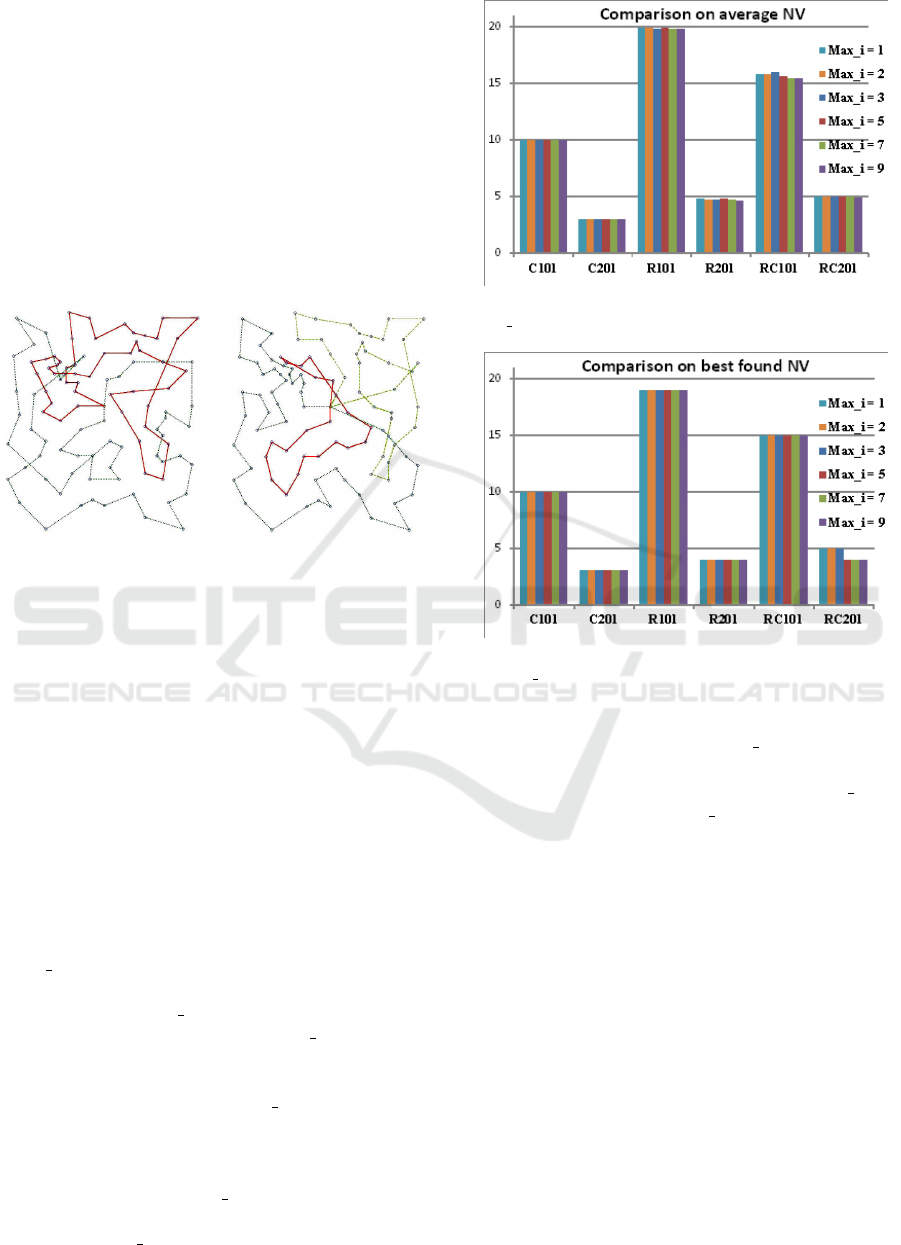
Figure 2: Two best found solutions with 2 and 3 vehicles on
R204.
It is also shown that VNS-C is effective in mini-
mizing TD by the results on the complicated datasets
(R2, RC2) which use fewer vehicles to satisfy 100 de-
mands. Thus it requires a powerful neighbourhood
operator to reduce NV. Figure 2 shows that the dispar-
ity between our best found solution (NV = 3 and TD
= 766.91) and the best known solution with a lower
NV (NV = 2 and TD = 825.52) on R204 is large,
which may mean that the distance between them is
large in the search space. It is difficult for VNS-C to
find a lower NV in this case, as the link length limit
in LinkMove-i (5) is too small compared to the route
length (33).
To investigate the performance of LinkMove-i on
reducing NV, six different upper bound values of i
(Max i) are set to this operator. Figures 3 and 4
demonstrate the performance of the LinkMove-i oper-
ator with diverse Max i on minimizing NV. In Figure
3 it can be seen that, the higher Max i can produce
a lower average NV on four complicated instances
(R101, R201, RC101 and R201) while the best found
NV is unchanged. Too small Max i would insert only
short routes to other routes, and the capability of re-
ducing NV would become weaker consequently. This
hypothesis is consistent to the observation on RC201
in Figure 4 that, when Max i is small (1, 2 and 3) the
best found NV (5) is greater than the one (4) found
with larger Max i values (5, 7 and 9). In addition,
Figure 3: Comparison on average NV with six different
Max i values of LinkMove-i.
Figure 4: Comparison on the best found NV with six differ-
ent Max i values of LinkMove-i.
experiment results also show that some of the lowest
TD can be found with small Max i, while their av-
erage NVs are the largest. e.g. the lowest TDs are
found on R101, RC101 and RC201 with Max i = 1,
as well as on R201 with Max i = 2. This observation
indicates the conflicting relation of both objectives on
these instances.
4 CONCLUSIONS
For problems with multiple objectives, local search
tends to be less effective. This paper explores a
variable neighbourhood search (VNS) algorithm with
compound neighbourhood operators (VNS-C) to op-
timize both objectives simultaneously in VRPTW. In
the proposed VNS-C, two compound neighbourhoods
are developed based on the Or-opt and CROSS ex-
change operators by considering specific features in
VRPTW. In addition, another neighbourhood opera-
tor LinkMove-i, which can reduce the number of ve-
hicles simultaneously, is also proposed.
A new compounding way concerning both opera-
A Variable Neighbourhood Search Algorithm with Compound Neighbourhoods for VRPTW
33

tion position and exchange link length is proposed in
the compound neighbourhoods. Experiment results
on benchmark datasets show that VNS-C produces
promising results comparing with the best known
solutions in the current literature. VNS-C shows
stronger performance in minimizing the total travel
distance compared to reducing the number of vehi-
cles. Two-phase methods may obtain lower number
of required vehicles in long-route instances. Hybrid
approaches, invoking two-phase algorithm and other
effective operators based on VNS, remain a promising
direction in our future work.
ACKNOWLEDGEMENT
This research was supported by Royal Society In-
ternational Exchanges Scheme, National Natural
Science Foundation of China (NSFC 71471092,
NSFC-RS 71311130142), Ningbo Sci&Tech Bureau
(2014A35006) and Department of Education Fujian
Province (JB14223). We would like to thank the re-
viewers for their valuable comments.
REFERENCES
Alvarenga, G. B., Mateus, G. R., and De Tomi, G. (2007).
A genetic and set partitioning two-phase approach for
the vehicle routing problem with time windows. Com-
puters & Operations Research, 34(6):1561–1584.
Br
¨
aysy, O. (2003). A reactive variable neighborhood search
for the vehicle-routing problem with time windows.
INFORMS Journal on Computing, 15(4):347–368.
Br
¨
aysy, O. and Gendreau, M. (2001). Metaheuristics for the
vehicle routing problem with time windows. Report
STF42 A, 1025.
Chiang, W.-C. and Russell, R. A. (1997). A reactive tabu
search metaheuristic for the vehicle routing problem
with time windows. INFORMS Journal on computing,
9(4):417–430.
Cook, W. and Rich, J. L. (1999). A parallel cutting-plane
algorithm for the vehicle routing problem with time
windows. Computational and Applied Mathematics
Department, Rice University, Houston, TX, Technical
Report.
Cordeau, J.-F., Desaulniers, G., Desrosiers, J., Solomon,
M., and Soumis, F. (2001). Vrp with time windows. In
The vehicle routing problem, pages 157–193. Society
for Industrial and Applied Mathematics.
de Oliveira, H., Vasconcelos, G., Alvarenga, G., Mesquita,
R., and de Souza, M. (2007). A robust method for
the vrptw with multi-start simulated annealing and
statistical analysis. In Computational Intelligence
in Scheduling, 2007. SCIS’07. IEEE Symposium on,
pages 198–205. IEEE.
Dueck, G. (1993). New optimization heuristics: The
great deluge algorithm and the record-to-record travel.
Journal of Computational Physics, 104(1):86–92.
Ergun,
¨
O., Orlin, J. B., and Steele-Feldman, A. (2006). Cre-
ating very large scale neighborhoods out of smaller
ones by compounding moves. Journal of Heuristics,
12(1-2):115–140.
Fleszar, K., Osman, I. H., and Hindi, K. S. (2009). A vari-
able neighbourhood search algorithm for the open ve-
hicle routing problem. European Journal of Opera-
tional Research, 195(3):803–809.
Ghoseiri, K. and Ghannadpour, S. F. (2010). Multi-
objective vehicle routing problem with time windows
using goal programming and genetic algorithm. Ap-
plied Soft Computing, 10(4):1096–1107.
Hansen, P. and Mladenovi
´
c, N. (2001). J-means: a new lo-
cal search heuristic for minimum sum of squares clus-
tering. Pattern recognition, 34(2):405–413.
Hansen, P., Mladenovi
´
c, N., and P
´
erez, J. A. M. (2010).
Variable neighbourhood search: methods and appli-
cations. Annals of Operations Research, 175(1):367–
407.
Hansen, P., Mladenovi
´
c, N., and Perez-Britos, D. (2001).
Variable neighborhood decomposition search. Journal
of Heuristics, 7(4):335–350.
Hansen, P., Mladenovi
´
c, N., and Uro
´
sevi
´
c, D. (2006). Vari-
able neighborhood search and local branching. Com-
puters & Operations Research, 33(10):3034–3045.
Hemmelmayr, V. C., Doerner, K. F., and Hartl, R. F. (2009).
A variable neighborhood search heuristic for periodic
routing problems. European Journal of Operational
Research, 195(3):791–802.
Jozefowiez, N., Semet, F., and Talbi, E.-G. (2008). Multi-
objective vehicle routing problems. European journal
of operational research, 189(2):293–309.
Kallehauge, B., Larsen, J., and Madsen, O. B. (2006). La-
grangian duality applied to the vehicle routing prob-
lem with time windows. Computers & Operations Re-
search, 33(5):1464–1487.
Kohl, N., Desrosiers, J., Madsen, O. B., Solomon, M. M.,
and Soumis, F. (1999). 2-path cuts for the vehicle rout-
ing problem with time windows. Transportation Sci-
ence, 33(1):101–116.
K
¨
uc¸
¨
uko
˘
g lu,
˙
I. and
¨
Ozt
¨
urk, N. (2014). An advanced hybrid
meta-heuristic algorithm for the vehicle routing prob-
lem with backhauls and time windows. Computers &
Industrial Engineering.
Laporte, G. (1992). The vehicle routing problem: An
overview of exact and approximate algorithms. Eu-
ropean Journal of Operational Research, 59(3):345–
358.
Lin, S. (1965). Computer solutions of the traveling sales-
man problem. Bell System Technical Journal, The,
44(10):2245–2269.
Mladenovi
´
c, N. and Hansen, P. (1997). Variable neigh-
borhood search. Computers & Operations Research,
24(11):1097–1100.
Ombuki, B., Ross, B. J., and Hanshar, F. (2006). Multi-
objective genetic algorithms for vehicle routing prob-
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
34

lem with time windows. Applied Intelligence,
24(1):17–30.
Or, I. (1976). Traveling salesman-type combinatorial prob-
lems and their relation to the logistics of regional
blood banking. Xerox University Microfilms.
Osman, I. H. (1993). Metastrategy simulated annealing and
tabu search algorithms for the vehicle routing prob-
lem. Annals of operations Research, 41(4):421–451.
Polacek, M., Hartl, R. F., Doerner, K., and Reimann, M.
(2004). A variable neighborhood search for the multi
depot vehicle routing problem with time windows.
Journal of heuristics, 10(6):613–627.
Potvin, J.-Y., Kervahut, T., Garcia, B.-L., and Rousseau,
J.-M. (1996). The vehicle routing problem with time
windows part i: tabu search. INFORMS Journal on
Computing, 8(2):158–164.
Rego, C. (1998). A subpath ejection method for the vehicle
routing problem. Management Science, 44(10):1447–
1459.
Rochat, Y. and Taillard,
´
E. D. (1995). Probabilistic diversi-
fication and intensification in local search for vehicle
routing. Journal of heuristics, 1(1):147–167.
SINTEF (2015). Best known solution val-
ues for solomon benchmark. http://
www.sintef.no/Projectweb/TOP/VRPTW/Solomon-
benchmark/100-customers/
Solomon, M. M. (1987). Algorithms for the vehicle rout-
ing and scheduling problems with time window con-
straints. Operations research, 35(2):254–265.
Taillard, . A., Badeau, P., Gendreau, M., Guertin, F. A., and
Potvin, J.-Y. (1997). A tabu search heuristic for the ve-
hicle routing problem with soft time windows. Trans-
portation science, 31(2):170–186.
Tan, K., Chew, Y., and Lee, L. (2006). A hybrid multi-
objective evolutionary algorithm for solving vehicle
routing problem with time windows. Computational
Optimization and Applications, 34(1):115–151.
Ursani, Z., Essam, D., Cornforth, D., and Stocker, R.
(2011). Localized genetic algorithm for vehicle rout-
ing problem with time windows. Applied Soft Com-
puting, 11(8):5375–5390.
Van Breedam, A. (1995). Improvement heuristics for the
vehicle routing problem based on simulated anneal-
ing. European Journal of Operational Research,
86(3):480–490.
A Variable Neighbourhood Search Algorithm with Compound Neighbourhoods for VRPTW
35