Combinatorial Identification of Broad Association Regions

with ChIP-seq Data

Jieun Jeong

, Mudit Gupta

, Andrey Poleshko

and Jonathan A. Epstein

Gastrointestinal Unit and Center for Computational and Integrative Biology, Massachusetts General Hospital,

Harvard Medical School, Boston, MA 02114, U.S.A.

Department of Cell and Developmental Biology, Institute for Regenerative Medicine, and the Penn Cardiovascular

Institute, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104, U.S.A.

Keywords: ChIP-seq Data, Regions of Protein Binding, Global Optimization.

Abstract: Motivation: Differentiation of cells into different cell types involves many types of chromatin modifications,

and mapping these modifications is a key computational task as researchers uncover different aspects of that

process. Modifications associated with heterochromatin formation pose new challenges in this context

because we must define very broad regions that have only a moderately stronger signal than the rest of the

chromatin. Lamin-associated domains (LADs) are a prime example of such regions. Results: We present

Combinatorial Identification of Broad Association Regions (CIBAR), a new method to identify these types

of broad regions. CIBAR is based on an efficient solution to a natural combinatorial problem, which adapts

to widely variable yields of reads from ChIP-seq data and the associated controls and performs competitively

with previous methods, including DamID, which has been used in many publications on LADs but cannot be

applied in most in vivo situations.

1 INTRODUCTION

It is now widely accepted that there are many types of

epigenetic chromatin modifications that profoundly

impact cellular phenotypes and thus all types of life

processes (Berstein et al, 2010). A typical task in

processing genome-wide data regarding such

modifications is to simplify the complex distribution

of these modifications into simple collections of

regions where they are present.

There is no universal gold standard concerning

present/absent decisions, but in general, we wish to

see reproducible results (thus removing or decreasing

the impact of data noise) that are associated with

biological outcomes of interest, such as activating or

repressing gene expression or the presence of other

modifications.

Because different modifications are associated with

diverse molecular mechanisms, they require different

computational tools. The best-investigated “regions

of presence” are so-called (narrow) peaks of

sequence-specific transcription factors, which can

have lengths around 100 bps. Broad peaks, with

lengths ranging from hundreds to thousands of bps,

are typical regions for the presence of chromatin

factors, e.g., chromatin-modifying enzymes that form

protein complexes with transcription factors but have

some mobility that allows them to modify longer

chromosomal intervals. A prime example of regions

with peaks and broad peaks are so-called promoters

and enhancers (Ernst et al., 2011), and even longer

broad peaks may be associated with regions with

Polycomb repression complex activity (Ernst et al.,

2011; Mikkelsen et al., 2007). In this note, we focus

on broad regions, which sometimes cover many

millions of base pairs, that in many cases are

associated with modifications that repress gene

expression in wide domains because they are

involved in the establishment of heterochromatin.

The tools for finding broad peaks are not adequate

for finding broad regions because they share the basic

assumption with tools for narrow peaks: namely, they

define locations that have a much higher normalized

concentration of ChIP reads than so-called

background locations. However, heterochromatin

covers most of the genome, and the modifications

associated with heterochromatin have a very wide

distribution; therefore, assumptions of that kind are

not applicable.

One type of chromatin modification that is attracting

Jeong, J., Gupta, M., Poleshko, A. and Epstein, J.

Combinatorial Identiﬁcation of Broad Association Regions with ChIP-seq Data.

DOI: 10.5220/0005663400270034

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 27-34

ISBN: 978-989-758-170-0

increasing attention is binding to lamins proteins

present in the nuclear lamina, as well as the lamina of

the nucleolus (Padeken and Heun, 2014).

The lamina lines the membranes of the nucleus and

nucleolus and forms a mesh-like structure that

stabilizes the position of a portion of the chromatin in

the nuclear periphery. Chromosomal regions where

contact with lamins is detected are called lamin-

associated domains (LADs); binding to lamins is

mediated through several proteins, and it is still under

investigation. The following proportions have been

reported in the mouse genome: (1) ca. 65% of

chromatin is heterochromatin (Ernst et al., 2011), (2)

ca. 40% of chromatin is in LADs (Guelen et al.,

2008), and (3) more than 90% of LADs are in

heterochromatin (this estimate is based on the

depletion of LADs with expressed genes [Table 1]).

It is important to note that eukaryotic genomes vary

widely in length and thus in gene density; hence,

those proportions should be different in different

species. The extent of heterochromatin changes

during cell differentiation, and these changes are part

of the processes that determine cell fate. In turn, a

number of chromatin factors have been implicated in

the formation of LADs.

Table 1: Joint length, the number of gene transcription start

sites (TSS) and the number of TSSs of expressed genes (E-

TSS, genes with an e9.5 expression level above the median)

for LADs identified by DamID and by CIBAR. We define

the consensus of the four e9.5 samples (three e12.5

samples) as windows that are selected to be in LADs for all

of them, with one possible exception, and we call the

resulting set "3 of 4" ("2 of 3" for e12.5 samples).

Computation of LADs includes the following three

basic stages, and for each stage we can choose a

method: (1) we obtain the data from the genome

(signal and control), (2) we convert the data to a

"normalized signal", and (3) we use the normalized

signal to determine regions where the normalized

signal values are mostly higher than in the remainder

of the genome.

There are two methods of collecting the binding

data for lamins and proteins that interact with lamins

for the purpose of genome-wide mapping of LADs.

The first is DamID (Guelen et al., 2008). In DamID,

the protein binding data are obtained by adding a

DNA methylating domain to the investigated protein.

Then, the loci with methylated DNA are identified by

hybridization to microarrays (with ca. 2.5 million

probes in the case of the mouse genome). These data

are paired with data in which the protein is augmented

with a “neutral” domain. The benefits are that no

specific protein antibodies are required and that the

control data match the signal data very well.

However, such genomic manipulation is impractical

in vivo; in particular, DNA methylation itself can

affect the phenotype. The second method is to collect

ChIP-seq using an antibody and input, which is the

associated control formed from a portion of the

starting material, i.e., the DNA from the respective

cell sample. The signal data that are collected are

quite uniformly distributed while methods of the

broad peak-type perform well only when we have a

high fold change between regions where we declare

the present compared with the remainder of the

chromatin.

The standard method for computing the

“normalized signal” from the data is to use ratios,

such as the “the number of ChIP reads” over “the

number of input reads.” However, we present our

alternative method in Section 2.

Several methods have been previously used to

identify broad regions from binding data.

The first method is a 2-state Hidden Markov

Model (HMM). The use of HMM for defining

genomic regions is well established (e.g., Ernst et al.,

2011) and seems indispensable when we integrate the

signals of multiple types. HMM has been used by Xu

et al. (2010) to compute the broad peaks from ChIP-

seq/input data, and is also a part of the DamID

method. However, when we have only one type of

signal, combinatorial algorithms are faster and offer a

better understanding of how the regions are defined,

and consequently, of how to set the parameters to

achieve the desired outcomes.

Lund et al. (2014) have tested several existing

programs for computing “long peaks” and have found

that all of them are inadequate for LADs. Another

combinatorial approach used to identify LADs is the

“sliding windows” method (Shah et al., 2013), in

which a long window consists of k short windows

(called steps). We accept a long window if it contains

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

some threshold number of short windows with the

positive score, and we declare LADs as the union of

the accepted long windows. An undesirable aspect of

this method is that it ignores the signal values that can

have considerable amplitudes and are not captured by

comparison with a threshold. Moreover, the user must

arbitrarily choose many parameters, including the

threshold on the values, the length of the long

windows and the minimum number of “positive”

short windows.

Those undesirable aspects are not present in a

method that uses a combinatorial problem defined in

terms of the sums of signal values (that can be

positive and negative) in the selected intervals. The

EDD method by Lund et al. (2014) incorporates the

following combinatorial problem: (1) we are given a

number of arrays with real values and (2) we find a

contiguous fragment with the maximum sum of

values. Then, we select that fragment and remove it

from its array, which may increase the number of

remaining arrays. We repeat this selection a desired

number of times, and finally we reject the selected

regional candidates that do not pass a permutation test

for significance.

Our CIBAR method has two major differences

from EDD. First, we use a different formula for

computing the signal values that more accurately

follows the dependency between the distribution of

the ChIP and input reads. Second, instead of selecting

the fragments one at a time, we apply a framework of

global optimization such that for a given array and k,

we select k array fragments in such a way that the sum

of all of the values in the selected fragments is

maximized. We also show a very efficient solution to

that problem.

2 METHODS - DESCRIPTION

OF CIBAR

2.1 Windows

We partitioned the genome into 1000 bp windows

(also known as bins) and each window has a position,

e.g., chr2:3001 for bps 3,001,001 to 3,002,000. Each

window w has a

input reads and b

ChIP reads.

Because the windows are merged into much longer

regions, the precise selection of the window length

has moderate importance. However, in our

experience, the average value of the a

, number of

input reads in a window should be in the range of 50.

We collected reads from several ChIP and input

sets, and we process only windows with at least one

read mapped in one of the sets. The other windows

are ignored, and we call them “null windows.” As a

result, we do consider windows with a

= b

= 0 if

they have reads in some other data sets.

2.2 Scores of Windows – The

Motivation

The “significance” of an interval of windows is

related to the p-value that we see for a particular

number of signal reads in that interval, but we

normalize that number on the basis of the number of

input (control) reads.

The question that we address in a novel way is

how to normalize the signal. ChIP reads are not

uniformly collected through the genome because of

the differences in the accessibility of different parts

of chromatin to the processes that generate the reads

(Kharchenko et al. 2008). In particular,

heterochromatin tends to be less accessible, and the

frequency of input reads in heterochromatin tends to

be lower. This motivates normalization approaches,

such as the ratio between the normalized ChIP and

input read counts.

The ratio approach is valid if the relationship

between the ChIP and input counts is linear.

However, this is not the case.

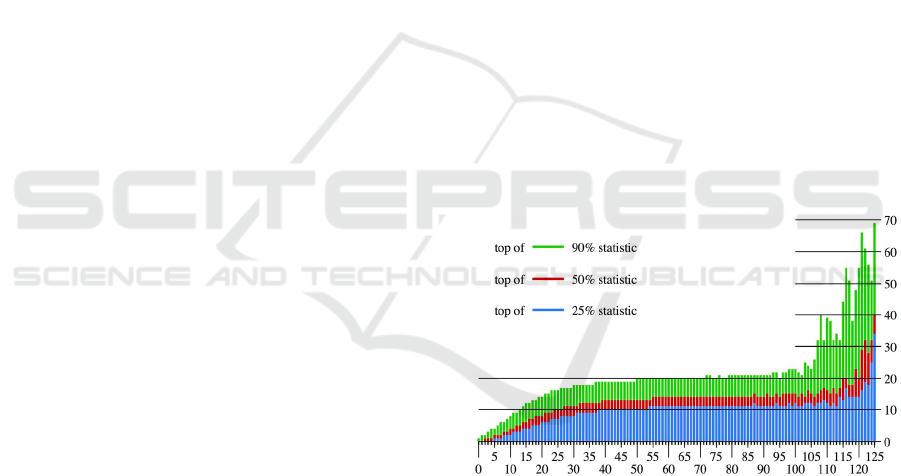
Figure 1: The X-axis is the a

, which is the number of input

reads in a 1 kbp window, and each bar represents the set of

all windows with a

indicated by the X-coordinate. The

heights of the colors for the Y-coordinate are the values of

, which are the numbers of ChIP reads that are order

statistics for this window set. The top of blue is 25% (the

highest value in the bottom quadrant), the top of red is 50%

(the median), and the top of green is 90% (the lowest value

in the top decile). Forty-four is the median level for the

input reads, less than 0.1% of the windows have more than

100 input reads, and because the sets for a

> 100 are very

small, their statistics change quite irregularly.

Figure 1 illustrates the distribution for a typical

input-ChIP pair. In that example, the input-ChIP

relationship is well approximated as linear between 0

Combinatorial Identiﬁcation of Broad Association Regions with ChIP-seq Data

and 20 input reads, and as constant between 30 and

100 input reads; i.e., the ChIP read counts are almost

independent of the input counts. For rare high counts

of input reads, the relationship is once again roughly

linear.

Normalization is important because 20-25% of

windows have low input counts and proportionally

smaller ChIP counts. Moreover, these windows are

primarily in the heterochromatin where we expect

LADs to be. However, for a wide range of input

values, linear normalization would be a significant

distortion. Our solution is to normalize the signals

separately for each possible number of input reads.

To our knowledge, previous work has made no

account of this problem. The use of ChIP-input ratio

did not produce very distorted results because the

effect is to exaggerate the link between LADs and

heterochromatin, although in actuality, this link is

very strong. However, in studies of embryonic

differentiation, etc., we are very much interested in

“marginal” LADs, where the dynamic extent of

LADs has regulatory impact on gene expression

without total heterochromatin silencing

characteristics. Thus, misclassification of LADs, over

1-5% of the genome can have a high impact on the

lists of genes whose regulation can be attributed to

LADs. Moreover, the positive bias for

heterochromatin can be detrimental when the method

is applied to regions associated with PRC activity or

gene elongation.

Other than separating the windows according to

their input counts, our method for computing the

signal is quite similar to the one by Lund et al. (2014).

2.3 Window Scores – The Formula

Given that a window w has a

input reads and b

ChIP

reads, we define the following statistics:

(1) n

is the number of all of the windows with a

= i,

(2) s

is the number of all of the windows with a

= i and b

= k, and

(3) A

is the average rank of windows with a

= i

and b

= k among all of the windows with a

= i, i.e., A

= s

+ … + s

i(k-1)

+ ½s

ik.

The score(i, k) = κ(2

), where

κ(x) = log x if x ≤ 1

and κ(x) = −log (2−x) if x ≥ 1.

Note that the score(i, k) is negative/zero/positive if A

is smaller/equal/greater than ½n

, respectively.

The idea of the scoring is that we prefer to select

windows with positive scores and to avoid selecting

windows with negative scores. However, with the

described method for assigning scores, about half of

the windows have positive scores, and about half have

negative scores, even though the target regions

occupy less than half of the genome. Therefore, we

use

score(w) = score(a

, b

) – α,

where α is the score adjustment, which is the same for

all of the non-null windows. The larger the score

adjustment we use, the fewer the windows belonging

to the selected regions. The score adjustment is one

of the two parameters supplied by the user.

This scoring formula is subjected to a high

statistical fluctuation when n

is small. If n

is smaller

than 1000, we enlarge the counts by forming a set of

windows of size 1000 or more, which have between

i−d and i+d input reads for the smallest possible d.

2.4 From Signal Values to Regions/

Domains

LAD signals computed with our formula exhibit large

random-like variability, in part because the collection

of reads, both input and ChIP, is essentially a random

process of extracting the reads from a library. In the

case of narrow and broad peaks, we observe

concentrations of ChIP reads that are many times

larger than background, although this is not the case

with the much less-concentrated signal that we see in

very broad regions. Instead, we can see a rather small

advantage of the positive signal that persists over a

long interval.

We identify our broad regions by solving the 1-

dimensional fragment selection (1DFS): given an

array with real values (scores of windows in

chromosomes) and a target number k, find k

disjointed fragments that are contiguous sub-arrays

and have the maximum sum of scores. The 1DFS

problem describes the optimization goals more

directly than the iterative formulation by Lund et al.

(2014). Importantly, exact solution of 1DFS can be

found efficiently in time proportional to n log n,

where n is the number of windows. This is slightly

slower than the speed of the algorithm in Lund et al.

(2014), but the probabilistic validation of the

computed regions takes approximately 10 times

longer and our entire computation takes about one

minute on a 1.7 Ghz Macintosh computer. Our

algorithm for 1DFS uses a greedy method and is easy

to implement.

We give the details of the 1DFS algorithm and the

proof of its correctness in the Appendix. To our

knowledge, this is a new algorithm that may have

more applications in genomic region studies.

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

3 RESULTS

We applied our method to laminB1 ChIP data

collected for the following two biological conditions

(ChIP was performed as described in Shah et al.

(2013)): (1) the mouse embryonic heart at e9.5 and

(2) the mouse embryonic heart at e12.5 (days after

conception), with four and three replicates,

respectively. These samples are subsequently referred

to as A-D and K-M, respectively. We found that using

an input with less than 50 million reads leads to erratic

results, so we used the same input for all of the ChIP

samples; it was collected from the e9.5 sample and

had 111 million reads. We set the target number of

LADs at 1500 and experimented with different

adjustment parameters. Adjustments that led to LADs

having much more than 800 Mbps in joint length had

a considerable proportion of regions with p-values

above 0.001, so we decided not to further increase the

size (see Appendix for the details of p-value test).

Then, we checked whether the LADs have the

properties previously reported in the literature. The

first property is that LADs are severely depleted of

genes and that the genes present in LADs are mostly

silent (very low expression level). We tested this on

18,988 genes that have annotations in refGene.txt for

the mm9 mouse genome build (available from UCSC

Genome Browser) and for which we also had

microarray expression data.

Table 1 shows that our LADs contain similar

numbers of genes and expressed genes as LADs

computed with the DamID method (see Peric-Hupkes

et al., 2010). DamID LADs cover 42-47% of the

genome, 14-18% of genes and 4-6% of expressed

genes. Our LADs (identified by CIBAR) cover 33-

34% of the genome, representing proportionally

fewer genes, and are also depleted expressed genes,

though not as much.

Taking a consensus of regions computed for the

same condition results in a similar depletion in

expressed genes as in DamID; consensus is an

effective method to eliminate false positives. We

defined the consensus as the base pairs that occur in

all or all but one of the LAD sets that were computed

for that condition; this is shown in Tables 1-3.

We also measured the level of consistency for the

LADs computed for the four cell types studied in

Peric-Hupkes et al. (2010) and our LADs from the

embryonic heart (see Table 2).

The degree of consistency between our embryonic

LADs and the LADs computed in Peric-Hupkes et al.

(2010) is similar to the consistency between those cell

types (note that among those four types, neural

pluripotent cells (NPC) and astrocytes, a

differentiated neural type, are the closest).

Table 2: Similarity of different LAD sets. For e9.5 and

e12.5, we use consensus regions (called “3 of 4” and “2 of

3”). The percentage of the smaller set that belongs to both

sets being compared is in red.

In Table 3 we compare EDD with CIBAR.

Both EDD and CIBAR produce LADs with

properties reported in Peric-Hupkes et al. (2010),

namely that they cover approximately 40% of the

genome (32-33% in the case of CIBAR and 34-36%

in the case of EDD) and that LADs are depleted in

genes, even more so in expressed genes, as we already

discussed. The consistency with DamID LADs is also

similar. CIBAR LADs have two advantages. First,

they are computed with 1 kbp windows, while EDD

automatically selects window sizes between 35 and

90 kbps, which means that the LAD boundaries are

much less precise. Second, EDD produced 200-275

LADs, and CIBAR produced 880-1280 LADs, which

is closer to what was previously reported.

Table 3: Comparison of results of CIBAR and EDD. The

column labels correspond to row labels in Table 1.

To a degree, this is a consequence of the parameters

we chose for CIBAR, namely the selection of the

Common Mbps % of the smaller set

Set Mbps e9.5 e12.5 Astro ESC MEF NPC

e9.5 721 565 584 581 600 594

78 81 81 83 82

e12.5 832 565 577 605 635 579

81 69 73 76 70

Astro 1112 582 577 772 881 931

81 69 72 78 87

ESC 1067 581 605 772 836 786

81 73 72 78 87

MEF 1179 600 635 881 836 880

83 76 78 78 82

NPC 1070 594 579 931 786 880

82 70 87 74 82

Combinatorial Identiﬁcation of Broad Association Regions with ChIP-seq Data

window size, target size (regulated by the adjustment)

and the target number of regions.

4 CONCLUSIONS

We presented a new method of computing broad

regions associated with chromatin modifications that

is applicable even when ChIP data do not exhibit

large fold changes between the affected regions and

the rest of the genome. Although our method was

conceived and implemented before the publication of

EDD (Lund et al., 2014), it shares the following three

aspects: (a) using scores of windows rather than a

selected cut-off between “good” and “bad” windows,

(b) basing the score number on the ranks of the

windows and (c) applying a natural combinatorial

problem to group windows into regions.

Our scoring method models the distributions of

ChIP and control reads more accurately; thus, we

avoid the positive bias for selecting windows in the

least accessible parts of the genome. It remains an

open question whether this is a good model, and we

expect further progress in this direction.

The combinatorial problem that we have

applied, 1DFS, is much more natural than the iterative

selection of fragments with the highest sum of scores,

which can excessively merge “positive” regions with

the “negative” regions that separate them. Lund et al.

(2014) introduced gap penalty (decreasing all

negative scores by a constant) to reduce that

tendency, but we suspect that this is one of the reasons

why EDD works with such low granularity. Although

1DFS is a global optimization problem, we have

found a solution that is very efficient and easy to

implement.

Our method uses only two parameters, k and α,

but the proper selection of parameters remains an

open problem. In Section 2, we set k to obtain the

number of LADs, which is close to the number

reported in papers applying the DamID method (see

Peric-Hupkes et al., 2010). Parameter α can be

selected in different ways. As it increases, the

proportion of windows with positive score(w)

decreases, as does the sum of lengths of identified

LADs. However, when we decrease α too much, the

p-values of the computed LADs tend to increase, and

we cannot suggest a statistic that allows to optimize

α. In fact, we tested our program and EDD on six

genes confirmed to be in LADs using ChIP-qPCR

(data not included). We found that increasing α may

paradoxically exclude some of them, whereas

choosing a consistent α of 0.12 led to consistent

inclusion of 5 of the genes in LADs computed for all

four e9.5 samples. LADs computed by EDD (which

automatically adjusts parameters to optimize the p-

values) consistently included exactly 3 of these genes.

This small evidence suggests that at present there is

no better way to select the parameters than using

whatever knowledge we have, most preferably some

genomic positions confirmed to be in LADs or

outside LADs, and picking the parameters to be

consistent with that knowledge. The situation with

identifying short peaks of transcription factors is

similar because the existing programs can produce

"false positives," i.e., statistically significant peaks

that are too weak to have a biological impact.

Therefore, these programs provide options to select

the parameters, such as maximum p-value/FDR,

minimum fold change.

REFERENCES

Bernstein BE et al. (2010) The NIH Roadmap Epigenomics

Mapping Consortium. Nature Biotechnol. 28(10),

1045-8.

Ernst, J. et al. (2011) Mapping and analysis of chromatin

state dynamics in nine human cell types. Nature,

473(7345), 43–49.

Guelen, L. et al. (2008) Domain organization of human

chromosomes revealed by mapping of nuclear lamina

interactions. Nature, 453(7197), 948–951.

Kharchenko, P. V. et al. (2008) Design and analysis of

ChIP-seq experiments for DNA-binding proteins. Nat.

Biotechnol., 26(12), 1351–1359.

Lund, E. et al. (2014) Enriched domain detector: a program

for detection of wide genomic enrichment domains

robust against local variations. Nucleic Acids Res.,

42(11), e92.

Mikkelsen, T. S. et al. (2007) Genome-wide maps of

chromatin state in pluripotent and lineage-committed

cells. Nature, 448(7153), 553–560.

Padeken, J. and Heun, P. (2014) Nucleolus and nuclear

periphery: velcro for heterochromatin. Curr. Opin.

Cell. Biol., 28, 54–60.

Peric-Hupkes, D. et al. (2010) Molecular maps of the

reorganization of genome-nuclear lamina interactions

during differentiation. Mol. Cell., 38(4), 603–613.

Shah, P. P. et al. (2013) Lamin B1 depletion in senescent

cells triggers large-scale changes in gene expression

and the chromatin landscape. Genes. Dev., 27(16),

1787–1799.

Xu, H. et al. (2010) A single-noise model for significance

analysis of ChIP-seq with negative control.

Bioiformatics, 26(9), 1199–1204.

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

APPENDIX – THE GREEDY

ALGORITHM FOR THE 1DFS

PROBLEM

1.1 Problem Definition

An instance of 1DFS consists of an array of real

values A[0] … A[n−1] and a positive integer k. A

fragment A[s, t] is specified by two distinct integers;

if s < t then it consists of A[s] … A[t−1], otherwise it

is a “wrap around” fragment that consists of A[s] …

A[n−1] and A[0] … A[t−1]. The value of a fragment

is the sum of its entries. The goal is to find j ≤ k

disjointed fragments with the maximum possible sum

of values.

Allowing the wrap-around fragments simplifies

the problem such that every entry has two neighbors,

left and right, that can join it in the same fragment.

Moreover, it is equivalent to find j disjoint and non-

adjacent fragments with the maximum sum of values

and to find j fragments with the minimum sum of

values because the complement of j disjoint and non-

adjacent fragments also consists of j disjoint and non-

adjacent fragments.

In our application, we have a number of arrays,

one for each chromosome. However, even though

1DFS has only one array and allows wrap-around

fragments, it is in fact equivalent. We can add an entry

with a very low negative value to the end of each of

those arrays and combine all of them into one. Then,

the “improper” fragments are formally allowed, but

they cannot be present in an optimal solution because

they have negative values.

1.2 Instances with Restricting

Partitions and the Greedy

Algorithm

We generalize problem instance by adding P, a

restricting partition of array A, into disjoint

fragments, and then we allow only fragments that are

unions of fragments from P in the solution. The

fragments from P can be numbered p

… p

−1

, and

we use A

[i] to denote the value of p

Our algorithm starts with the restricting partition of

A into 1-entry fragments and then applies the rules

described in Figure 2 until it terminates. The

algorithm is greedy in the sense that the rules are very

simple, and it either terminates or applies a rule that

reduces the size of the problem (the number of

fragments in the restricting partition).

Use the first applicable rule from the following list:

(1) Terminating Rule. If P contains k or fewer

fragments with positive values, return the set of

these fragments.

(2) Equal Sign Rule. If p

and p

i+1

both have

negative values or both have non-negative values,

merge them together.

(3) Minimum Value Rule. Select i with the

minimum | A

[i] |, merge together p

i-1

, p

and p

i+1.

Figure 2. The rules in the algorithm for the 1DFS

problem.

1.2.1 Correctness of the Terminating Rule

The sum of the values from the selected fragments

cannot exceed the sum of the values from all of the

positive fragments in P; thus, the value of the returned

solution is optimal, and because there are at most k

such fragments, the solution is valid.

1.2.2 Correctness of the Equal Sign Rule

Suppose that the solution S is consistent with the

former restricting partition but not with the new one.

Then, a fragment of S (F, for example) contains p

but

excludes p

or vice versa. If the value of p

negative, we can modify F by excluding p

, thus

increasing the value of F and S; this works because p

is at the end of F. Similarly, if the value of p

is non-

negative, we can modify F by extending it with p

which before was fully excluded from the solution,

and the value of the solution will increase or stay the

same because the value of p

is also non-negative.

Thus we defined a solution S’ that has the same value

as S and is consistent with the new partition.

1.2.3 Correctness of the Minimum

Value Rule

Because the Termination Rule does not apply, the

number of the positive restriction fragments is l > k.

Because the Equal Sign Rule does not apply, the

fragments of P with negative and non-negative values

alternate, so the number of P-fragments is equal to 2l

> 2k.

Suppose that solution S is consistent with the

former restricting partition, P, but not with the new

one P’. This means that the fragments of S contain

some but not all of p

−1

, p

and p

. We can assume

that S cannot be improved by extending or shrinking

one of its fragments by one P-fragment. Hence, in

every fragment of S, the first and the last P-fragment

have positive values, and in every fragment of the

complement of S, the first and last P-fragment has

negative values. Thus, each fragment of S and of the

Combinatorial Identiﬁcation of Broad Association Regions with ChIP-seq Data

complement of S consists of an odd number of

restriction fragments.

Case 1: Fragments of S contain only p

−1

. We can

extend S by incorporating p

and p

, and the value of

S increases by A

[i+1]−|A

[i]| ≥ 0.

Case 2: Fragments of S contain only p

, so the

restriction fragment p

is also a fragment of S. We

remove p

from S, which decreases the value of S by

x, which is the value of p

. We have to modify S to

increase its value by x or more. Because we have

decreased the number of fragments in S, the

modification is allowed to increase the number of

fragments by 1. Because there are more than 2k

restriction fragments, one of the fragments of S or the

complement of S (F, for example) contains at least

three restriction fragments. If F is a fragment of S, it

contains a restriction fragment p

with a negative

value –y. We remove p

from F, which increases the

number of fragments by one and increases the value

of the solution by y ≥ x. If F is a fragment of the

complement of S, it contains a restriction fragment p

with a positive value y, so we add p

to S. Again, the

number of fragments in S increases by 1 and the value

by y≥x. Importantly, as p

neither starts nor ends F,

it cannot be p

−1

or p

Other cases are symmetric, so every solution that

satisfies the restriction before we applied the merging

can be modified to a solution that satisfies the new

restriction with a value that is the same or larger.

Implementation

We first compute a matrix with read counts for every

data sample (input and ChIP) and every window, and

we then use that matrix (tab separated file) as the

input for our C-program. Null windows, those

without any reads, are ignored as “unmappable”.

In the program, we use an array of doubly linked

lists for fragments in the restriction partition, with one

list for each chromosome. The fragments are also

represented in a binary heap (priority queue), which

allows rapid application of the Minimum Value Rule.

To assess the p-value of computed regions, we

used the null model in which the scores of windows

are randomly permuted. We found out that for regions

with more than 200 windows, the p-value can be well

approximated using the cumulative Gaussian

distribution. For fewer windows, we use one million

runs of 200 random window selections, which

allowed us to tabulate empirical p-values for all of the

region sizes up to 200 windows. As a result, this

Monte Carlo test adds less than a minute to the

computation time and uses very little additional

memory.

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms