Gene Selection using a Hybrid Memetic and Nearest Shrunken

Centroid Algorithm

Vinh Quoc Dang and Chiou-Peng Lam

School of Computer & Security Science, Edith Cowan University, Perth, Australia

Keywords: Memetic Algorithm, Nearest Shrunken Centroid, Microarray, Feature Selection, Classification.

Abstract: High-throughput technologies such as microarrays and mass spectrometry produced high dimensional

biological datasets both in abundance and with increasing complexity. Prediction Analysis for Microarrays

(PAM) is a well-known implementation of the Nearest Shrunken Centroid (NSC) method which has been

widely used for classification of biological data. In this paper, a hybrid approach incorporating the Nearest

Shrunken Centroid (NSC) and Memetic Algorithm (MA) is proposed to automatically search for an optimal

range of shrinkage threshold values for the NSC to improve feature selection and classification accuracy.

Evaluation of the approach involved nine biological datasets and results showed improved feature selection

stability over existing evolutionary approaches as well as improved classification accuracy.

1 INTRODUCTION

Recent reviews (Hilario and Kalousis, 2008) have

described numerous feature selection techniques for

identifying informative biomarkers from biological

datasets. The two main objectives of feature

selection is achieving high classification accuracy

and high reproducibility of a pertinent list of

biomarkers (i.e. feature selection stability). Stability

is a term used to describe the sensitivity of a feature

selection algorithm to small variations in the training

data and in the settings of the algorithmic

parameters, resulting in different feature sets being

produced by the algorithm.

Many studies (Kim et al., 2010; Yu and Liu,

2004), have used the Nearest Shrunken Centroid

(NSC) algorithm (Tibshirani et al., 2002) for feature

selection (FS) and classification in high dimensional

biomedical data. This algorithm, with its most well-

known software implementation being known as

Prediction Analysis for Microarrays (PAM), requires

a shrinkage threshold value as input for performing

FS and classification. The choice of this threshold

value, as stated in the PAM User guide, is

determined “after a judicious examination of

training errors and the cross-validation results”.

Hence, the selection of the optimal shrinkage

threshold value is typically a manual process based

on “trial and error” by setting the shrinkage

threshold value to vary equally using a predefined

step size across a predefined range (Lusa, 2012).

However, shrinkage threshold values selected in this

way may not give optimal solutions (Dang et al.,

2013) and is also a very time consuming process.

A hybrid approach (NSC-GA) (Dang et al.,

2013), incorporating GA and NSC to automatically

find the optimal shrinkage threshold value.

Computation time associated with GA processing

can be intensive (Elbeltagi et al., 2005) . One of the

approaches to improve GAs both in terms of

computation time and quality of optimal solutions is

the use of a memetic algorithm (MA) (Elbeltagi et

al., 2005).

In this paper, an approach of incorporating the

NSC algorithm into a MA, namely NSC-MA, for

automatically searching for an optimal range of

shrinkage threshold values is proposed. The aim

here is to explore how to improve the NSC-GA

approach (Dang et al., 2013) for achieving

robustness of selected feature subsets and stability in

signatures of biomarkers. Unlike NSC-GA, the

proposed approach consistently reproduces the same

candidate feature subset from repeated runs

involving a dataset.

The rest of the paper is organized as follows:

Section 2 reviews some related work, Section 3

describes details of the proposed approach, datasets,

results and discussion are presented in Section 4, and

conclusion is drawn in Section 5.

190

Dang, V. and Lam, C-P.

Gene Selection using a Hybrid Memetic and Nearest Shrunken Centroid Algorithm.

DOI: 10.5220/0005665201900197

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 190-197

ISBN: 978-989-758-170-0

2 RELATED WORK

Chin et al., (2015) completed a comprehensive

review of feature selection methods for gene

selection, categorising these into three classes,

namely supervised, unsupevised and semi-

supervised. Each of these 3 classes are further

refined into sub-categories on the basis of evaluation

criterion into filter, wrapper or embedded methods.

Statistical metrics are used in filter methods to rank

each feature individually or subsets of features for

its ability to discriminate between classes. In

wrapper-based methods, classification models are

used to determine the relevance of sets of features

and embedded methods are similar to wrapper

methods except for a much tighter coupling between

feature selection and classifier. Feature selection is

NP-hard and can be approximated via a heuristic

search for an "optimal" feature subset. In conclusion,

Chin et al., (2015) discussed a number of areas

needing future research, amongst these, is the need

to develop methods for robustness of selected

feature subsets (i.e. stability of signature).

Dang et al., (2013) developed a wrapper

approach (NSC-GA) involving genetic algorithm

and NSC and evaluated the approach on microarray

data. Similar to PAM (Tibshirani et al., 2002), the

selection of subsets of features utilize a penalized t-

statistic but the approach automatically determines

the required soft-threshold for identifying a gene

set for classification. Experimental results show that

the optimal threshold value obtained using NSC-GA

resulted in a smaller number of features and higher

classification accuracies on test datasets in

comparison to previous studies such as Klassen and

Kim (2009).

Soufan et al., (2015) developed a web-based,

wrapper feature selection tool using a parallel GA as

its search strategy that allows concurrent evaluations

of large number of candidate subsets. The tool is

flexible for its range of filtering methods as well as

its functionality of allowing for adjustments of

weights and parameters in the fitness function.

Zhu et al., (2007b) incorporated a memetic

algorithm (MA) in their approaches, namely

WFFSA and MBEGA (Zhu et al., 2007a) for finding

relevant features in microarray data. Both these

approaches were based on the traditional GA and a

local search (LS) algorithm that incorporated filter

ranking method for WFFSA and Markov Blanket for

MBEGA respectively. Binary representation (1, 0)

was the encoding for individuals and the SVM

classifier was employed to evaluate the fitness of

individuals. Empirical evaluations of these two

approaches on microarray datasets indicate that they

outperformed many existing methods in terms of

classification accuracy, number of selected genes

and search efficiency.

3 NSC-MA PROPOSED

APPROACH

MA is a hybrid of EAs which involves an

evolutionary algorithm (EA) and a local search (LS)

to improve the fitness of chromosome (Krasnogor

and Smith, 2005; Wu, 2001). As shown in Figure 1,

the 2 major steps in NSC-MA are:

Step 1: This step involved the automatic

calculation of Th

max

. This procedure is performed

once only at the beginning of the proposed approach,

NSC-MA, to obtain Th

max.

Step 2: MA (Moscato, 1989) is employed in this

step as an optimization method to search for optimal

sets of shrinkage thresholds for NSC algorithm that

lead to the selection of optimal sets of features. NSC

algorithm is employed as a fitness evaluator to

evaluate the fitness of each chromosome in terms of

the number of selected features and its

corresponding training classification accuracy.

Figure 1: Framework of the proposed approach, NSC-MA,

using MA with adding and subtracting Improvement First

Strategy LS.

Gene Selection using a Hybrid Memetic and Nearest Shrunken Centroid Algorithm

191

Gene value in each chromosome in the population is

initialized to a real value within the range of [0,

max

] using a random number generator. The

random number generator uses a different seed for

each initialization of a new population. Details

associated with determination of Th

max

can be found

in Dang et al., (2013).

3.1 Fitness Evaluation

The NSC algorithm (Tibshirani et al., 2002) is the

fitness evaluator for obtaining the overall fitness,

Fitness

Ind

, for each individual chromosome. As

defined in Equation (1), Fitness

Ind

is calculated by

averaging the fitness values associated with all the

threshold values for a chromosome.

Fitness

∑





/ M

(1)

where M is a number of genes or threshold values in

a chromosome.

The function f

in Equation (2) consists of two

other functions, f

and f

= f

+ f

(2)

= (N

total

- N

att

) / N

total

(3)

TP+TN

TP+FP+TN+FN

(4)

where TP is the true positives, TN is the true

negative, FP is the false positive, FN is the false

negative. N

total

equals to the total number of

attributes (features) in the dataset, N

att

is the number

of attributes selected by NSC. f

is designed for

evaluating the fitness of a threshold that leads to a

minimum number of attributes, whilst f

associated with the maximum classification

accuracy.

3.2 Generating New Population

The procedure for generating a new population using

MA incorporated adding and subtracting LS with

Improvement First Strategy is as follows:

Input:

Chromosome population (p)

Fitness population (F

)

Crossover probability (P

)

Mutation probability (P

)

Elite chromosome (Elite)

Chromosome length (len

)

Output:

New population (N

)

Steps:

1. Set Size=size of population, p

2. Set new population (N

)={∅}

3. Store Elite into N

4. For counter from 1 to ½ Size

a. Select 2 parent chromosomes

using binary tournament selection

i. Select 2 chromosomes randomly

from p

 Select the best fit chromosome as

parent (parent

)

ii. Select 2 chromosomes randomly from

 Select the best fit chromosome as

parent (parent

)

b. Create 2 offspring chromosomes using

parent

and parent

i. Generate a random number (R

) in

the range [0, 1] using RNG

ii. If R

≤ P

 Perform one point crossover on 2

parents to produce offspring

and

offspring

 Perform adding and subtracting LS

with Improvement First Strategy

on offspring

and offspring

produce 2 new offspring

(offspring

cross

and

offspring

cross

)

iii. If R

≤ P

For counter from 1 to len

 Generate a random number

) in the range [0, 1]

using RNG

If R

≤ P

 Perform uniform mutation on

each bit of offspring

generate offspring

1mut

 Perform uniform mutation on

each bit of offspring

generate offspring

2mut

 Perform adding and

subtracting LS with

Improvement First Strategy

on offspring

1mut

and

offspring

2mut

to produce 2

new offspring

(offspring

mut

and

offspring

mut

)

iv. Evaluate fitness of

offspring

cross,

offspring

cross

offspring

mut

and offspring

mut

chromosomes

c. Store the best 2 chromosomes into N

This step involved the “adding and subtracting LS

with Improvement First Strategy” step, which is

applied to offspring chromosomes after crossover

and mutation in order to further improve its quality.

A single elitist strategy is employed where the

best candidate solution (elite) from the previous

generation is placed into the new population. To

produce new offspring, Binary Tournament selection

is used to select the individuals as parents to go

through crossover, mutation and LS strategy. Two

best offspring chromosomes from each of these

iterations are then placed into the new population.

The procedure for the “adding and subtracting

LS with Improvement First Strategy” step is as

follows:

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

192

Input:

Chromosome (chrom)

Chromosome length (len)

Output:

An improved local search chromosome

(chrom

)

Steps:

1. Generate a real random number (R

)

in the range [0,1] using RNG

2. Evaluate fitness of chrom

3. set fitness of chrom

4. set counter=1

5. While (counter<=len) and (fitness

chrom

<=fitness chrom)

a. Add R

to chrom[counter] to

create a new chromosome (chrom

)

b. Evaluate the fitness of chrom

c. If fitness of chrom

> chrom

Retain chrom

as an improved

local search chromosome

d. Else

 subtract R

to chrom[counter]

create a new chromosome

(chrom

)

 evaluate the fitness of chrom

 If fitness of chrom

> chrom

retain chrom

as an improved

local search chromosome

 Else

discard chrom

update counter=counter+1

3.3 Parameter Settings

Table 1: Parameter settings used in the proposed approach

NSC-MA.

Parameters Values/Algorithm

Population size 30

Chromosome length 10

Crossover rate 0.6

Mutation rate 0.0333

Maximum generation 1000

Selection Binary Tournament

Crossover Single point

Mutation Uniform

Elitist Single

Local search

Adding and subtracting with First

Improvement Strategy

The parameter settings for running NSC-MA are

shown in Table 1. The parameters that are tuned

include population size, crossover probability rate,

and mutation probability rate, with these values in

the table, being taken from an empirical experiment

(Dang, 2014). Uniform mutation (Eiben and Smith,

2007) modifies a chromosome by replacing its gene

value with a mutated number, N

mut

, which is

calculated using equation (5).

= L

+ (R

* (U

- L

)) (5)

where L

is lower bound of chromosome, R

is a

random number generated by RNG, U

is upper

bound of chromosome.

4 RESULTS AND DISCUSSION

Table 2 showed a summary of the nine datasets that

have been used widely by many recent

investigations as demonstrated in Chin et al (2015).

These include: AD Disease (Ray et al., 2007), Colon

(Alon et al., 1999), Leukemia (Golub et al., 1999),

Ovarian (Petricoin et al., 2002), Lymphoma

(Alizadeh et al., 2000), Lung (Gordon et al., 2002),

Prostate (Singh et al., 2002), Central Nervous

System (CNS

) (Pomeroy et al., 2002) and Breast-

A (van't Veer et al., 2002) that we used to evaluate

NSC-MA. Each dataset is partitioned into a training

dataset and an unseen test set using either the same

configuration as proposed by their original authors

(as cited for each dataset mentioned above), or those

of other authors who have used the same datasets in

their studies.

Table 2: Summary of nine public datasets used for the

NSC-MA approach.

Dataset Type of data

No of

attr.

No of

classes

No of

Samples

Protein

Immunoa-ssay

120 2 259

Colon

Cancer

microarray

2000 2 62

Leukemia 7129 2 72

Lung 12533 2 181

Lymphoma 4026 2 47

Prostate 12600 2 136

CNS 7129 2 60

Breast-A 1213 3 98

Ovarian

Proteomic

spectra

15154 2 253

For each of the nine datasets, 15 independent

runs of NSC-MA were executed using the respective

training dataset and parameter values shown in

Table 1. Each independent run involved an initial

population produced using the Random Number

Generator with a random seed. For each run, 10 fold

cross validation (CV) strategy was employed to

evaluate the selected feature sets. The optimal set of

features was then used to construct the NSC

classifier to classify the unseen test data associated

with the dataset. The average classification accuracy

was calculated from these runs.

A simple multi-start local search algorithm

(MSLS) based on a local search method (Lourenço

et al., 2001) was implemented for comparison of

performance with NSC-MA. 15 independent runs of

Gene Selection using a Hybrid Memetic and Nearest Shrunken Centroid Algorithm

193

MSLS were also executed using the respective

training dataset.

The results are examined from 2 perspectives:

diagnostic relevance in terms of features used in the

construction of accurate diagnostic classifiers for

prediction and by examination of the literature for

the established implication of the selected set of

features to specific diseases (Table 4). Table 3

showed comparisons of results from NSC-MA with

MSLS and other studies using equivalent protocol,

that is training a classifier using a training set and

evaluation of performance involved an unseen test

set. NSC-MA consistently selected only one set

features over 15 independent runs. This shows that

the stability of NSC-MA is improved over NSC-GA.

For example for Colon cancer dataset, NSC-GA

selected 2 sets of 6 and 28 features, whilst NSC-MA

selected only one set of 28 features, for Lung cancer

dataset, NSC-GA selected 4 sets of 8, 9, 10 and 11

features whilst NSC-MA selected only one set of 8

features with the same classification accuracy of

100%. With the AD, CNS and Breast-A datasets,

both NSC-MA and MSLS returned the same results

but with the remaining 6 datasets, there is a lot more

variability in terms of the number of selected subsets

as well as the number of features in the respective

feature subsets from employing MSLS, thus

demonstrating that NSC-MA has better feature

selection stability over MSLS.

NSC-MA achieved very similar classification

results to NSC-GA. In comparison to other existing

techniques, NSC-MA achieved better classification

results in most cases using a smaller feature sets.

The set of 11 features associated with the AD dataset

is a subset of the 18 identified by Ray et al., (2007).

For the Colon dataset, it is not possible to check the

set of 28 genes found by the proposed approach

against the set of 16 genes in Klassen and Kim

(2009) as these were not listed in their study.

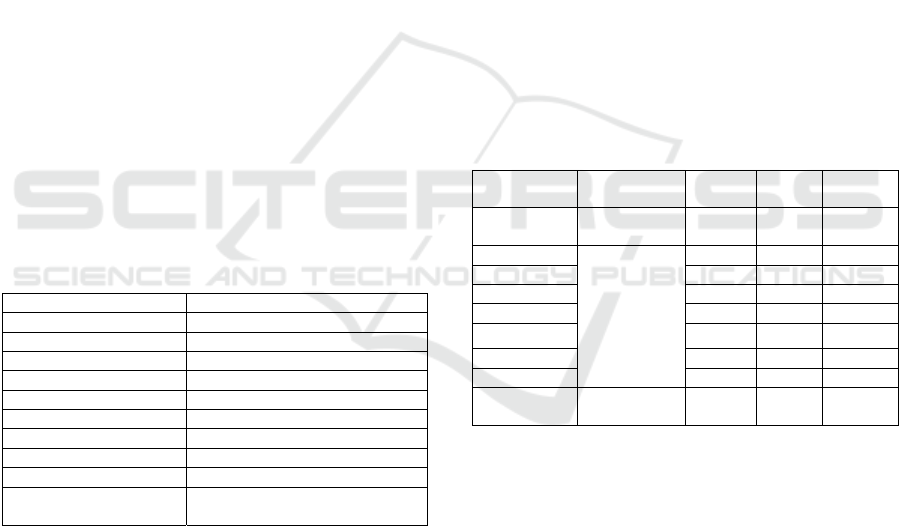
Table 3: Summary of results obtained from the NSC-MA approach in comparison with existing approaches. Each cell

indicates the average unseen test classification % and the number of selected genes in () associated with 15 independent

runs. In cells with multiple entries, this is associated with some of the 15 runs returning different subsets of features.

Approach AD Colon Leukemia Ovarian Lymphoma Lung Prostate CNS Breast-A

Proposed

approach

NSC-MA

89.34

(11)

100

(28)

97.05

(9)

96.06

(7)

100(128) 100(8) 90.2(6) 65.51(3) 89.58(2)

NSC-GA(Dang

et al., 2013)

89.49

(11)

93.75

(6)

100

(28)

97.05

(9)

96.06

(7)

95.45(7)

95.45(12)

100(128)

100(129)

100(132)

100(8)

100(9)

100(10)

100(11)

90.2(6) 65.51(3) 89.58(2)

NSC (Ray et

al., 2007)

(18)

NSC (Klassen

and Kim, 2009)

75(16)

94.12

(21)

86.6(25) 93.7(5) 90.91(6)

ALP-NSC,

AHP-NSC

(Wang and Zhu,

2007)

94.12

(16)

Weighted NSC

(Tai and Pan,

2007)

99.55(6)

60.51

(10)

FAIR (Gordon

et al., 2002)

97.05

(11)

95.3(31) 73.52(2)

GCLUS &

SERA

(Baggiolini et

al., 1989)

97.63

(47)

Multi-Start

Local Search

(MSLS)

88.62

(11)

93.75 (1)

93.75(6)

100(28)

93.75(29)

87.5(34)

87.5(35)

91.17(1)

91.17(2)

91.17(3)

96.06(7)

96.06(36)

96.06(37)

96.06(38)

95.45(7)

100

(128, 130, 132,

135, 137, 139,

145, 140, 151)

100(8)

100(9)

100(10)

100(11)

88.23(3)

88.23(4)

90.2(5)

90.2(6)

65.51(3)

89.58

(2)

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

194

Table 4: The sets of features selected by NSC-MA for nine datasets AD, Colon, Leukemia, Ovarian, Lymphoma, Lung,

Prostate CNS and Breast-A.

Dataset

No of

Attr

Acc No

AD 11

PDGF-BB_1 RANTES_1 IL-1a_1 TNF-a_1 EGF_1 M-CSF_1 ICAM-1_1 IL-11_1 IL-

3_1 GCSF_1 ANG-2_1

Colon 28

T95018, X55715, M63391, H40560, T92451, T57619, R78934, T58861, M26697,

M76378, R87126, H43887, H64489, M22382, T71025, Z24727, Z50753, X12671,

T47377, L05144, H55758, M64110, M76378, T60155, M76378, J02854, X86693,

T60778

Leukemia 9 M27891, M84526, M96326, U46751, U50136, X17042, X95735, M28310, Y00787

Ovarian 7

MZ244.36855, MZ244.66041, MZ244.95245, Z245.24466, MZ245.8296,

MZ245.53704 and MZ246.12233

Lymphoma 7

GENE3327X, GENE3329X, GENE3330X, GENE3332X, GENE3361X,

GENE3258X, GENE3256X

Lung 8 32551_at, 33328_at, 34320_at, 36533_at, 37157_at, 37716_at, 37954_at, 40936_at

Prostate 6 31444_s_at, 41468_at, 37639_at, 38406_f_at, 769_s_at and 556_s_at

CNS 3 L17131_rna1_at, Yo7604_at, U33448_s_at

Breast-A 2 LY6D, ESR1

In the case of the Leukemia cancer dataset, NSC-

MA obtained a smaller set of 9 genes and

classification accuracy of 97.05% when compared

to 96% using 10 genes in (Huang, 2009) with 2

genes (M27891, X95735) in common. Eight genes

(M27891, M84526, M96326, U46751, U50136,

X95735, M28130, Y00787) are a subset of the set of

48 features selected using GA and ANNs in (Tong et

al., 2009).

This nine gene is also a subset of the set of 50

highly expressed genes identified by (Masys et al.,

2001) for predicting disease from non-disease. For

the Ovarian cancer dataset, NSC-MA identified a set

of 7 features, MZ244.36855, MZ244.66041,

MZ244.95245, Z245.24466, MZ245.8296,

MZ245.53704 and MZ246.12233 which is a subset

of the 47 peptides reported in Foss (Foss, 2011),

with similar classification accuracy of 96.06% on

the unseen test set. Six peptides in this set are among

the top 10 peptides identified in Yap et al., (2007).

In terms of the Lung cancer dataset, using a set of 6

features, Tai and Pan (2007) achieved 99.55%

whereas NSC-MA used 8 features and obtained

100% classification accuracy on the unseen test set.

However, the identified features have not been listed

in Tai and Pan’s paper. For the Breast cancer

dataset, NSC-MA identified a set of 2 features,

LY6D (Lymphocyte antigen 6 complex, locus D)

and ESR1 (Estrogen receptor 1). LY6D is strongly

expressed in cervical cancer, head and neck cancer,

lung cancer, skin cancer and urothelial cancer, and

also a marker of the earliest stage of B-cell

specification (GeneCards; The Human Protein

Atlas). ESR1 is cancer and disease related genes,

and also involved in pathological processes in

endometrial and breast cancer (The Human Protein

Atlas).

To obtain an overall estimate of the

computational effort of using NSC-GA and NSC-

MA to analyse the nine datasets, we collected the

total time taken for each of their 15 independent

runs. The average time taken by NSC-GA is 1290.39

minutes and 1219.56 minutes for NSC-MA.

5 CONCLUSIONS

The shrinkage threshold value must be provided as

an input to the NSC algorithm and an appropriate

choice is extremely important in terms of feature

selection and classification accuracy. Researchers

have used approaches of trial and error to select a

threshold value that produced minimum

classification errors and some emerging work has

investigated approaches to automatically produce

this value. A novel approach incorporating NSC and

MA algorithm is proposed in this study in order to

overcome limitations of the previous approaches

such as empirical methods with NSC and NSC-GA.

Evaluation of the approach involved nine biological

datasets and results showed improved feature

selection stability over existing evolutionary

approaches as well as improved classification

accuracy.

REFERENCES

Alizadeh, A., Eisen, B., Davis, E., Ma, C., Lossos, I. S.,

Rosenwald, A., Yu, X. (2000). Distinct types of

Gene Selection using a Hybrid Memetic and Nearest Shrunken Centroid Algorithm

195

diffuse large B-cell lymphoma identified by gene

expression profiling. Nature, 403(6769), 503-511.

Alon, Uri, Barkai, Naama, Notterman, Daniel A, Gish,

Kurt, Ybarra, Suzanne, Mack, Daniel, & Levine,

Arnold J. (1999). Broad patterns of gene expression

revealed by clustering analysis of tumor and normal

colon tissues probed by oligonucleotide arrays.

Proceedings of the National Academy of Sciences,

96(12), 6745-6750.

Baggiolini, Marco, Walz, A, & Kunkel, SL. (1989).

Neutrophil-activating peptide-1/interleukin 8, a novel

cytokine that activates neutrophils. Journal of Clinical

Investigation, 84(4), 1045.

Chin, A., Mirzal, A., Haron, H., & Hamed, H. (2015).

Supervised, Unsupervised and Semi-supervised

Feature selection: A Review on Gene Selection.

Dang, V. (2014). Evolutionary approaches for feature

selection in biological data. (PhD), Edith Cowan

University, Australia.

Dang, V., Lam, C., & Lee, C. (2013). NSC-GA: Search for

optimal shrinkage thresholds for nearest shrunken

centroid. Paper presented at the Proceedings IEEE

sympodium series on computatinal intelligence,

Singapore.

Eiben, A. E., & Smith, J. E. (2007). Introduction to

evolutionary computing. Berlin Heidelberg: Springer.

Elbeltagi, Emad, Hegazy, Tarek, & Grierson, Donald.

(2005). Comparison among five evolutionary-based

optimization algorithms. Advanced Engineering

Informatics, 19(1), 43-53.

Foss, Andrew. (2011). High-dimensional Data Mining:

Subspace Clustering, Outlier Detection and

Applications to Classification: VDM Publishing.

GeneCards.). LY6D Gene. Retrieved 10 December,

2015, from http://www.genecards.org/cgi-

bin/carddisp.pl?gene=LY6D.

Golub, Todd R, Slonim, Donna K, Tamayo, Pablo, Huard,

Christine, Gaasenbeek, Michelle, Mesirov, Jill P,

Caligiuri, Mark A. (1999). Molecular classification of

cancer: class discovery and class prediction by gene

expression monitoring. Science, 286(5439), 531-537.

Gordon, Gavin J, Jensen, Roderick V, Hsiao, Li-Li,

Gullans, Steven R, Blumenstock, Joshua E,

Ramaswamy, Sridhar, . . . Bueno, Raphael. (2002).

Translation of microarray data into clinically relevant

cancer diagnostic tests using gene expression ratios in

lung cancer and mesothelioma. Cancer Research,

62(17), 4963-4967.

Hilario, M., & Kalousis, A. (2008). Approaches to

dimensionality reduction in proteomic biomarker

studies. Briefings in Bioinformatics, 9(2), 102-118.

Huang, Liang-Tsung. (2009). An integrated method for

cancer classification and rule extraction from

microarray data. J Biomed Sci, 16(1), 25.

Kim, Gilhan, Kim, Yeonjoo, Lim, Heuiseok, & Kim,

Hyeoncheol. (2010). An MLP-based feature subset

selection for HIV-1 protease cleavage site analysis.

Artificial Intelligence in Medicine, 48(2-3), 83-89.

Klassen, M., & Kim, N. (2009). Nearest shrunken centroid

as feature selection for microarray data.

Paper

presented at the ICATA (Computers and Their

Applications).

Krasnogor, Natalio, & Smith, Jim. (2005). A tutorial for

competent memetic algorithms: model, taxonomy, and

design issues. Evolutionary Computation, IEEE

Transactions on, 9(5), 474-488.

Lourenço, Helena R, Martin, Olivier C, Stützle, Thomas,

Glover, Ed F, & Kochenberger, G. (2001). Iterated

Local Search. arXiv preprint math.OC/0102188.

Lusa, Lara. (2012). Impact of class-imbalance on multi-

class high-dimensional class prediction. Metodoloski

zvezki, 9(1), 25.

Masys, Daniel R, Welsh, John B, Fink, J Lynn, Gribskov,

Michael, Klacansky, Igor, & Corbeil, Jacques. (2001).

Use of keyword hierarchies to interpret gene

expression patterns. Bioinformatics, 17(4), 319-326.

Moscato, Pablo. (1989). On evolution, search,

optimization, genetic algorithms and martial arts:

Towards memetic algorithms. Caltech concurrent

computation program, C3P Report, 826, 1989.

Petricoin, EF, Ardekani, AM, Hitt, BA, Levine, PJ,

Fusaro, VA, Steinberg, SM, Liotta, LA. (2002). Use of

proteomic patterns in serum to identify ovarian cancer.

The Lancet, 359(9306), 572 - 577.

Pomeroy, SL, Tamayo, P, Gaasenbeek, M, Sturla, LM,

Angelo, M, McLaughlin, ME, Golub, TR. (2002).

Prediction of central nervous system embryonal

tumour outcome based on gene expression. Nature,

415, 436 - 442.

Ray, Sandip, Britschgi, Markus, Herbert, Charles, Takeda-

Uchimura, Yoshiko, Boxer, Adam, Blennow, Kaj,

Karydas, Anna. (2007). Classification and prediction

of clinical Alzheimer's diagnosis based on plasma

signaling proteins. Nature medicine, 13(11), 1359-

1362.

Singh, Dinesh, Febbo, Phillip G, Ross, Kenneth, Jackson,

Donald G, Manola, Judith, Ladd, Christine, Richie,

Jerome P. (2002). Gene expression correlates of

clinical prostate cancer behavior. Cancer Cell, 1(2),

203-209.

Soufan, O, Kleftogiannis, D, Kalnis, P, & Bajic, VB.

(2015). DWFS: A Wrapper Feature Selection Tool

Based on a Parallel Genetic Algorithm. PLoS ONE,

10(2), e0117988.

Tai, F., & Pan, W. (2007). Incorporating prior knowledge

of gene functional groups into regularized discriminant

analysis of microarray data. Bioinformatics, 23(23),

3170-3177.

The Human Protein Atlas.). ESR1. Retrieved 10

December, 2015, from http://www.proteinatlas.org/

ENSG00000091831-ESR1/gene.

Tibshirani, R., Hastie, T., Narasimhan, B., & Chu, G.

(2002). Diagnosis of multiple cancer types by

shrunken centroids of gene expression. Proc Natl

Acad Sci USA, 99(10), 6567 - 6572.

Tong, Dong L, Phalp, Keith T, Schierz, Amanda C, &

Mintram, Robert. (2009). Innovative hybridisation of

genetic algorithms and neural networks in detecting

marker genes for leukaemia cancer. Paper presented at

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

196

the 4th IAPR International Conference in Pattern

Recognition for Bioinformatics, Sheffield, UK.

van't Veer, Laura J, Dai, Hongyue, Van De Vijver, Marc J,

He, Yudong D, Hart, Augustinus AM, Mao, Mao, . . .

Witteveen, Anke T. (2002). Gene expression profiling

predicts clinical outcome of breast cancer. Nature,

415(6871), 530-536.

Wang, S., & Zhu, J. (2007). Improved centroids estimation

for the nearest shrunken centroid classifier.

Bioinformatics, 23(8), 972-979.

Wu, Fengjie. (2001). A Framework for Memetic

Algorithms. (Master of Science in Computer Science),

University of Auckland, Auckland.

Yap, E., Tan, H., & Pang, H. (2007). Learning causal

models for noisy biological data mining: An

application to ovarian cancer detection. Paper

presented at the AAAI.

Yu, L., & Liu, H. (2004). Redundancy based feature

selection for microarray data. Paper presented at the

Proceedings of the tenth ACM SIGKDD international

conference on Knowledge discovery and data mining.

Zhu, Z., Ong, Y., & Dash, M. (2007a). Markov blanket-

embedded genetic algorithm for gene selection.

Pattern Recognition, 40(11), 3236-3248.

Zhu, Z., Ong, Y., & Dash, M. (2007b). Wrapper–filter

feature selection algorithm using a memetic

framework. Systems, Man, and Cybernetics, Part B:

Cybernetics, IEEE Transactions on, 37(1), 70-76.

Gene Selection using a Hybrid Memetic and Nearest Shrunken Centroid Algorithm

197