
Geometry Analysis of Superconducting Cables for the Optimization of
Global Performances
Nicolas Lermé
1,2∗
and Petr Dokládal
1
1
MINES ParisTech, PSL Research University, Centre for Mathematical Morphology, Fontainebleau, France
2
Institut d’Électronique Fondamentale, Université Paris-Sud, Gif-sur-Yvette, France
Keywords:
Segmentation, Registration, Shape Analysis, Clustering, Superconductivity, Cable.
Abstract:
Superconducting cables have now become a mature technology for energy transport, high-field magnets (MRI,
LHC) and fusion applications (ToreSupra, and eventually ITER and DEMO). The superconductors are ex-
tremely brittle and suffer from electrical damages brought by mechanical strain induced by electromagnetic
field that they generate. An optimal wiring architecture, obtained by simulation, can limit these damages.
However, the simulation is a complex process and needs validation. This validation is performed on real 3D
samples by the means of image processing. Within this objective, this paper is, to our best knowledge, the
first one to present a method to segment the samples of three types of cables as well as a shape and geometry
analysis. Preliminary results are encouraging and intended to be later compared to the simulation results.
1 INTRODUCTION
1.1 Motivation and Scope
Superconducting cables have now become a mature
technology in energy transport, high-field magnets
(medicine (MRI), high-energy physics (LHC)) and
magnetic confinement in fusion applications (Tore-
Supra, eventually ITER and DEMO reactors).
A superconducting cable presents a multiscale in-
ternal structure. Such a cable consists of strands ar-
ranged together given some application-dependent ar-
chitecture. Individual strands are composite struc-
tures either formed by superconducting microfila-
ments embedded in a metallic matrix or a thin super-
conducting layer deposited onto a metallic substrate.
A substantial drawback of some of these cables
is the fragility of the superconductors. Mechanical
strains can indeed cause deformations, thus degrading
their performance.
Whereas these strains can be limited during shap-
ing (wiring or winding) or thermal cool-down, they
remain problematic during operation when exposed
to high electromagnetic fields due to its own Lorentz
∗
This work was funded by the ANR project ANR-
GUI-AAP-05 (2013–2017) and performed during the post-
doctoral research project of Nicolas Lermé at the Centre for
Mathematical Morphology.
force (particularly under cyclic loading).
However, the performance degradation can be di-
minished by optimizing the geometry of the cables.
Optimize the performance of these cables is thus es-
sential and could directly benefit to a large number of
research and industrial actors.
The global performances of the cable are simu-
lated using models of the electrical and/or mechani-
cal behavior of the cable structure (Torre et al., 2014;
Manil et al., 2012). Given the complexity of vari-
ous types of cables, the validation of these models
is done by statistical comparison of the geometry of
the models to the geometry of real cables obtained
from tomography images. Depending on the result of
these comparisons, the design of the cables can be op-
timized, until a better cable architecture is obtained.
This paper focuses on the identification of the
experimental geometry on three types of cables, in-
volving mostly
2
automatic registration, segmenta-
tion, clustering and features extraction tasks. To our
best knowledge, this is the first paper providing meth-
ods and results for the geometry analysis on these ca-
bles. For each type of cable, we provide below the
physical parameters and the image characteristics.
2
The method for segmenting cables-in-conduit is semi-
automatic since initial manual markers are required.
540
Lermé, N. and Dokládal, P.
Geometry Analysis of Superconducting Cables for the Optimization of Global Performances.
DOI: 10.5220/0005667105400551
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 540-551
ISBN: 978-989-758-173-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(a) N05 (b) N22 (c) mgb2_113 (d) 18RRPN01 (e) 40RRPR02
Figure 1: Cross-sectional images from cables-in-conduit (a,b), power cables (c) and Rutherford cables (d,e).
Table 1: Image characteristics (top) and physical parameters (bottom) of the cables-in-conduit (left to the double bar) and
power cables (right to the double bar).
N05 N22 N25 mgb2_113 mgb2_133
Image size (x, y,z)
750 ×800×12431 750×850×12424 750 ×750×7745 1200 ×1200×5972 1300 ×1605×6071
Resolution (µm)
12 12 12 10 10
Memory usage (GB)
6.94 7.37 4.05 8.1 12
Number of s.c./n.s.c. (all) strands
30/15(45) 15/30(45) 30/15(45) 24/37(61) 24/37(61)
Strand (µm)
800 800 800 1130 1330
Avail. sample length (µm)
149172 149088 92940 59270 60710
Twist-pitch sequence (mm)
45/85/125 45/85/125 35/65/110
227 260
First triplet (s.c.,n.s.c.)
(2,1) (1,2) (2,1)
/ /
Cable pattern
(3,3,5) (3,3,5) (3,3,5)
/ /
Void fraction (%)
25 33 33 24.7 24.7
1.2 Available Cables
Three distinct types of cables are considered with
different architectures, appearances and composition:
the cables-in-conduit (Weiss et al., 2007), the Ruther-
ford cables (Oberli, 2013; Milanese et al., 2012)
and the power cables (Seidel and Sturge, 2009; IEC,
2004). Several samples of each with different param-
eters were analyzed (see Tab. 1 and 2 for their charac-
teristics, and Fig. 1 to assess the variety and the qual-
ity of the images).
Cables-in-conduit (see Fig. 1(a,b)) consist of su-
perconducting strands (s.c.) and non-superconducting
strands (n.s.c.). S.c. strands are composed of kernels
in Nb
3
Sn and bronze (white) wrapped by a jacket in
copper (gray) while n.s.c. strands are made of copper
(gray). All strands are twisted together in a multistage
fashion according to a predefined cable pattern com-
posed of stages and petals. For instance, the pattern
(3,3,5) of the cable N05 has three stages. The first
(lower) stage consists of twisted triplets (15 petals),
each with 2 s.c. and 1 n.s.c. strands. These triplets
are again twisted by three (5 petals) and finally by
five (1 petal), thus leading to a total of 30 s.c. and
15 n.s.c. strands. All strands are then inserted in a
stainless steel conduit. Some void fraction is kept to
enable the circulation of a cooling fluid (helium). No-
tice that all stages are twisted with a different twist-
pitch. Typically used in fusion applications, these ca-
bles can transport currents of 45kA under a magnetic
field of 12.3T, exposed to transversal Lorentz forces
of 554kN/m.
Power cables (see Fig. 1(c)) consist of s.c. strands
in MgB
2
/nickel alloy and n.s.c. copper strands. All
strands are arranged in concentric layers, twisted and
inserted in a corrugated cryogenic envelope. Again,
some void fraction is kept to enable the circulation of
a coolant (gaseous and eventually liquid helium). S.c.
strands are located on the outer layer. Typically used
in energy distribution, each strand can convey a cur-
rent of 400A under a magnetic field of 1T, developing
radial, centripetal, Laplace forces of 400N/m.
Rutherford cables (see Fig. 1(d,e)) roughly consist
of s.c. strands composed of cores in copper (gray) sur-
rounded by an intermediary zone containing Nb
3
Sn
filaments (white), themselves wrapped in a copper
jacket (gray). All strands are twisted to form a two-
layers flat cable, compressed to a well-controlled rect-
angular section. Depending on the design used, the
filaments zone is arranged to form either an hexagon
or a circle. Typically used in medical imaging and
high-field magnets, these cables can transport cur-
rents of the order of 20kA under a magnetic field of
10 −15T, exposed to Lorentz forces of 1−5MN/m.
1.3 Outline of the Paper
The rest of this paper is as follows. In Section 2, we
briefly explain the registration of overlapping sam-
ples. In Section 3, we detail, for each type of cable,
the proposed methods for extracting the structures of
interest from the resulting images. In Section 4, we
Geometry Analysis of Superconducting Cables for the Optimization of Global Performances
541

Table 2: Image characteristics (top) and physical parameters (bottom) of the Rutherford cables.
COP-RRP 18PITN01 18PITN01_2 18RRPN01 18RRPN01_2 40RRPR01 40RRPR02
Image size (x, y,z)
1500 ×
300 ×1300
750 ×
1100 ×1200
1600 ×500 ×
1200
1100 ×
750 ×1200
1700 ×700 ×
1200
1600 ×
500 ×1200
1500 ×
500 ×1200
Resolution (µm) 15 10 6.75 10 6 15 15
Memory usage (MB) 558 945 916 945 1434 916 859
Number of strands 40 18 18 18 18 40 40
Strand (µm) 1050 1020 1000 1050 1046 1080 1035
Avail. sample length (µm) 19500 12000 8100 12000 7200 18000 18000
propose indicators reflecting potential damages. Fi-
nally, we present results in Section 5 and discuss fu-
ture work in Section 6.
2 IMAGE REGISTRATION
The cable samples being too long to be imaged at
once, multiple overlapping scans have been acquired
with a constant translation step along the z-axis
3
.
Each scan has then been registered on the previous
one by minimizing the Mean Square Error (MSE) of
the difference of intensities over the overlapping re-
gion along the z-axis. The minimization along the z-
axis is sufficient since no residual displacement along
the x and y axes was observed. The Fig. 2 depicts the
MSE as a function of the varying overlap between two
successive scans, for a cable-in-conduit (N05) and a
power cable (mgb2_113).
Figure 2: MSE of two overlapping scans for a cable-in-
conduit (left) and a power cable (right).
3 IMAGE SEGMENTATION
The purpose of the segmentation is to extract the con-
tours of strands (and the conduit, if need be) and their
centerlines. Most structures to extract are nearly cir-
cular and touch each other. Their appearance and con-
trast however differ for all cable architectures. Dis-
tinct algorithms have been designed for all types of
cables with their own set of parameters. Some of
these parameters still require a manual tuning (in this
case, it will be mentioned below). However, most of
them appear to be stable and expressed with respect
to the image resolution and cables characteristics.
3
From here, the z-axis will refer to the longitudinal one
while x,y axes will refer to transversal ones.
These algorithms share common difficulties to
overcome to get reliable measurements. First, they
must be able to assess slight deviations from the cir-
cularity, be robust to noise, artifacts and poor contrast.
Second, they must be fast and able to handle large vol-
ume data (possibly more than shown in Tab. 1 and 2).
To accommodate these constraints, a simple approach
has been preferred (whenever possible) where the 3D
volume is segmented as a sequence of 2D images
along the z-axis. This allows to run some steps in par-
allel. Once strand contours have been obtained, the
centerlines consist of the strand centroids. Moreover,
we assume the following known and constant: the di-
ameter of a strand (denoted by S
dr
), the thickness of
the strand jacket (denoted by S
jt
), the thickness of the
conduit of the cable (denoted by C
ct
) as well as the
number of s.c. and n.s.c. strands (denoted by N
sc
and
N
nsc
, resp.).
3.1 Rutherford Cables
The core of strands being better contrasted than the
jackets, we propose an automatic procedure that relies
on the filaments zone to extract the contours of strands
in two steps (see Fig. 3).
3.1.1 Extraction of Cores
First, an Alternate Sequential Filter (ASF) is applied
on the source image with a squared structuring ele-
ment up to the size of 0.03 ×S
dr
(Sternberg, 1986)
(image I
D
(a)). This allows us to both denoise the im-
age and fill the interstices between filaments. Next, a
filling algorithm is applied on the image I
D
(image
I
F
(b)). The image I
F
is then subtracted from the
image I
D
(image I
A
(c)). Once the image I
A
thresh-
olded (image I
T
(d)), it both contains cores and in-
terstices. To discard the interstices, a mask is built
by thresholding the image I
F
(image I
T
0
(e)) and ap-
plying a morphological erosion with a square of size
0.15 ×S
dr
as structuring element (image I
M
(f)). Fi-
nally, the mask I
M
is intersected with the image I
T
and
the 3D N
sc
largest connected components are kept.
The resulting components are labeled and correspond
to the cores (image I
C
(g)). Due to the variety of im-
ages, notice that the above thresholds need to be man-
ually adjusted, independently of ground truths (see
Section 5.1.1).
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
542

(a) I
D
(b) I
F
(c) I
A
(d) I
T
(e) I
T
0
(f) I
M
(g) I
C
(h) I
DM
(α = 10
4
) (i) I
R
(α = 0) (j) I
R
(α = 10
4
) (k) I
R
(α = 10
6
) (l) I
R
0
Figure 3: Steps for extracting the cores (a-g) and the strands (h-l) from an image of a Rutherford cable (COP-RRP). The source
image is first denoised by an ASF (a). Once (a) filled (b), it is subtracted from (a), giving (c). An intermediate result (d) is
obtained by thresholding (c). A mask (f) is built by thresholding (b) (giving (e)) and applying a morphological erosion on the
result (f). (f) is then intersected with (d) and the 3D N
sc
largest connected components are kept. The resulting components
are labeled and correspond to the cores (g). A region-growing algorithm is then used to extract the filaments zone, based on
geodesic distance maps whose amount of regularity is controlled by a parameter α (h). The impact of α after region-growing
is shown when it is small (i), moderate (j), large (k). The strands are obtained by expanding the filaments zone with α = 0 (l).
3.1.2 Extraction of Strands
As shown in Fig. 3, the filaments zone is poorly con-
trasted and strands touch with each other. To over-
come these difficulties, we introduce several priors
(near circularity, small displacement and volume con-
servation of strands sections) and proceed in two suc-
cessive steps.
First, a distance transform is computed from each
labeled core of I
C
using an efficient pixel queue al-
gorithm (Ikonen, 2005). This algorithm has a worst-
case complexity of O(n log n) (where n is the number
of pixels in the image). Each distance map is com-
puted using the WDTOCS metric, described in (Iko-
nen, 2005). Let I : Ω ⊂ Z
2
→ R be an image and
N be a neighborhood. Without loss of generality, we
propose to use
N = {(p,q) ∈ (Ω ×Ω) | kp −qk ≤
√
2},
where k.k is the L
2
norm in Z
2
. For any pair (p, q) ∈
N , the WDTOCS metric is defined as
dist(p, q) =
q
kp −qk
2
+ α(I
p
−I
q
)
2
, (1)
where α ∈ R
+
is a parameter that balance geometric
and image information. The larger the parameter α
is, the more the image information is taken into ac-
count. An example of distance map from the right-
most core is shown in (h) where the distance is pro-
portional to the intensity (the dynamic of the image
has been stretched for visualization purpose). Dis-
tance transforms being independent from each other,
their computation is in practice performed in parallel
using OpenMP. Once all the distance maps obtained
using α > 0, a region-growing algorithm is applied
to obtain the outer contour of the filaments zones: all
cores grow simultaneously by greedily selecting the
pixels having the minimum cost based on their respec-
tive distance maps, until a target volume is reached
4
.
The effect of varying the parameter α after region-
growing is depicted on the image I
R
when α is small
(i), moderate (j) and large (k). Finally, the contours of
strands are obtained by expanding the filaments zones
in such a way that none of them is favored. This is
achieved by repeating the above steps for α = 0 (im-
age I
R
0
(l)). In our experiments, we set α = 10
4
.
3.2 Cables-in-conduit
As shown in Fig. 4, the s.c. strands are better con-
trasted than the n.s.c. ones. Based on this observation,
we propose a three-steps scheme that first extracts au-
tomatically the conduit and then the s.c. strands. The
n.s.c. strands are then semi-automatically extracted
based on initial markers.
3.2.1 Extraction of the Conduit
First, the source image is denoised by an ASF with a
squared structuring element up to the size of 0.05 ×
S
dr
(Sternberg, 1986) (image I
D
(a)). To further flat-
ten homogeneous areas, the image I
D
is filtered by a
Gaussian of size 0.05 ×S
dr
and thresholded (image
I
T
(b)). Next, a morphological opening, a holes filling
algorithm and then a morphological closing are ap-
plied on the image I
T
using a square of size 0.2 ×S
dr
as structuring element (image I
M
(c)). Assuming the
ideal conduit is nearly circular, an ellipse is fitted on
the image I
M
. Its size is subtracted by 2×C
ct
to fit the
inner contour of the conduit (image I
R
(d)).
4
It is adjusted if the filaments zone is an hexagon.
Geometry Analysis of Superconducting Cables for the Optimization of Global Performances
543

(a) I
D
(b) I
T
(c) I
M
(d) I
R
(e) I
T
0
(f) I
F
(g) I
W
(h) I
R
0
(i) I
C
(j) I
R
00
(z = 0) (k) I
R
00
(z = 6211) (l) I
R
00
(z = 12423)
Figure 4: Steps for segmenting the conduit (a-d), the s.c. strands (e-h) and the n.s.c. strands (i-l) from an image of a cable-in-
conduit (N22). The source image is first denoised by an ASF (a). Next, (a) is filtered by a Gaussian and thresholded (b). Holes
are filled in (b) by various morphological operations (c). An ellipse is then fitted on (c) and adjusted on the inner contour of
the conduit (d). Once the conduit obtained, (a) is thresholded from the source image (e), dilated and filled (f). Using (d) and
(f), kernels are obtained by applying a watershed algorithm (g) on the source image. S.c. strands (h) are then extracted by
expanding (g) (same approach as Rutherford cables with α = 0) and subtracting the complement of (d). Finally, n.s.c. strands
are extracted with α > 0 (j-l), constrained by (d) and (h) but from the strands centroids f the previous image (i).
3.2.2 Extraction of the S.C. Strands
The strategy employed here is to rely on kernels to ex-
tract the contours of strands. For doing so, the source
image is first thresholded (image I
T
0
(e)). Next, the
resulting contours are closed using a morphological
dilation with a square of size 0.25×S
jt
as structuring
element and holes are filled (image I
F
(f)). To prop-
erly align the segmentation on the contours of kernels,
a watershed algorithm (Meyer, 1991) is applied on the
source image (image I
W
(g)). The outside marker is
the complementary of the image I
F
and the markers
representing the kernels are obtained by performing a
morphological erosion of the image I
F
with a squared
structuring element of size 1.25 ×S
jt
. As for Ruther-
ford cables, s.c. strands are finally obtained by ex-
panding the kernels from the image I
W
with α = 0
(see Section 3.1.2) and subtracting the complement
of the mask I
R
(image I
R
0
(h)).
3.2.3 Extraction of the N.S.C. Strands
To overcome the poor contrast on n.s.c. strands,
we adopt the same strategy as for Rutherford cables
(see Section 3.1.2) but with two differences. First,
the geodesic distances are computed using α > 0
but constrained in I
R
0
\I
R
. Second, the centroids of
s.c. strands must be provided as initialization (image
I
C
(i)). Geodesic distance maps are computed from
these centroids and the region-growing algorithm is
applied. Once the centroids computed on the result-
ing contours of strands, the same procedure is applied
on the next image (image I
R
00
). This process contin-
ues until the end of the cable is reached. To illustrate
the correctness of the propagation, the image I
R
00
is
shown with the n.s.c. strands obtained at the begin-
ning (j), the middle (k) and the end (l) of the cable.
Unlike Rutherford cables, it is important to notice that
such an approach can fail to recover the contours of
n.s.c. strands since centroids depend on the result of
the previous image. Such a situation can occur when
the contribution of the right term in Eq. 1 is insuf-
ficient. In that case, the procedure becomes unable
to stick to the contours of strands. A suitable value of
the parameter α must therefore be chosen carefully. In
our experiments, we have chosen to set α = 8 ×10
4
.
3.3 Power Cables
For extracting strands, a convenient solution would be
to use the same approach as for Rutherford cables (see
Section 3.1.2) and for the n.s.c. strands of the cables-
in-conduit (see Section 3.2.3). As shown in Fig. 1,
despite the important amount of noise, the images of
power cables present however a much better contrast
compared to the images of the other types of cables.
We detail below a simple procedure that automatically
find the contours of the conduit and then the strands,
both assumed to be nearly circular.
First, the source image is thresholded (image I
T
(a)) and holes are filled (image I
F
(b)). From the
image I
F
, the largest connected component is dis-
carded and a morphological opening is applied with
a squared structuring element of size 0.1×C
ct
(image
I
O
(c)). An ellipse is then fitted on the image I
O
. Its
size is subtracted by C
ct
to fit the inner contour of the
conduit (image I
R
(d)).
Second, the source image is denoised by an ASF
with a squared structuring element up to the size of
0.05 ×S
dr
(image I
D
(e)) (Sternberg, 1986). A first
rough estimate of the contours of strands is obtained
by thresholding the image I
D
(image I
T
0
(f)). The
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
544

(a) I
T
(b) I
F
(c) I
O
(d) I
R
(e) I
D
(f) I
T
0
(g) I
I
(h) I
H
(i) I
DM
(j) I
M
(k) I
S
(l) I
R
0
Figure 5: Steps for segmenting the conduit (a-d) and the strands (i-l) of a power cable (mgb2_113). First, the source image is
thresholded (a) and filled (b). From (b), the largest connected component is discarded and a morphological opening is applied
(c). An ellipse is fitted on (c) and adjusted on the inner contour of the conduit (d). Second, the source image is denoised by
an ASF (e) and thresholded (f). The complement of (d) is subtracted from (f) and a morphological opening is applied (g). 3D
connected components that do not spread all along the cable are removed (h). The Euclidean distance to the contours of (h)
is computed, filtered (i) and maxima are identified (j). Strands contours are obtained by applying a watershed (l) on an image
(k) combining the morphological gradient of the source image and the inverted distance map to ideal contours from maxima.
complement of the mask I
R
is then subtracted from
the image I
T
0
and a morphological opening is applied
with a square of size 0.03×S
dr
as structuring element
(image I
I
(g)). Next, 3D connected components that
do not spread all along the cable in the background
are removed (image I
H
(h)). From the image I
H
, the
Euclidean distance to the contours is computed and
the resulting image is filtered by a Gaussian of size
0.25 ×S
dr
(image I
DM
(i)) to ensure a good detection
of maxima (image I
M
(j)). Finally, the contours of
strands are obtained by applying a watershed (Meyer,
1991) performed on the summed image I
S
(k) com-
posed of the inverted distance map to ideal contours
from maxima and the morphological gradient (multi-
plied by a factor set to 0.1) of the source image (image
I
R
0
(l)). The multiplier ensures the strands sections to
remain mostly circular along the cable.
4 DAMAGE INDICATORS
During operation, the cables can be exposed to
transversal Lorentz forces up to several MN/m. These
forces induce deformation and/or damages to strands
that come out as various geometrical features. The
features detailed below aim at detecting these defor-
mations.
4.1 Strand Section Compression
Any deviation to the circularity of strands is a poten-
tial source of damage that need to be measured. A
variety of shape descriptors has been proposed in the
literature. In this setting, desirable properties of shape
descriptors are the invariance to translation and rota-
tion, the robustness to noise and a reasonable sensitiv-
ity. The papers (Montero, 2009; Žuni
´
c, 2012) gather
a large number of descriptors, out of which two have
been selected as applicable in this context and of-
fering similar performance. Let S ⊂ Z
2
be a strand
section of a 2D binary image taken along the z-axis.
These two descriptors are defined as follows:
EF(S) =
λ
max
λ
min
∈ [1,+∞[ (Elongation Factor),
where λ
min
, λ
max
are the eigenvalues of the covariance
matrix of the strand section S, and
CMPN(S) =
(]S)
2
2π(µ
2,0
+ µ
0,2
)
∈]0,1] (Compactness),
where ] denotes the cardinality of a set and µ
p,q
de-
notes the moment of order (p + q) of the strand sec-
tion S. EF and CMPN are statistical descriptors. EF
is lower-bounded by one for a circle and increases
for elongated shapes while CMPN is upper-bounded
by one for a circle and tends to zero for elongated
shapes. These two descriptors verify the above men-
tioned properties.
4.2 Curvature
For all the considered types of cables, strands can lo-
cally bend significantly and these locations are poten-
tially source of damage. Do detect bendings with a
large amplitude, we propose to measure the local cur-
vature of the strand centerlines.
The curvature measures a failure of a curve to be
straight. It is is positive or null and equal to the in-
verse of the radius of the tangent circle.
Let us represent a centerline with a two times
continuously differentiable space curve C (t) =
(x(t),y(t),z(t))
T
∈ R
3
, parameterized by t. Also, we
Geometry Analysis of Superconducting Cables for the Optimization of Global Performances
545

denote resp. by γ
0
(t) and γ
00
(t) the first and second and
derivatives of C with respect to t. The local curvature
of the curve C is defined by
κ(t) =
kγ
0
(t) ×γ
00
(t)k
kγ
0
(t)k
3
, (2)
where k.k and × are respectively the L
2
norm and
the cross product, both in R
3
. In what follows, we
briefly discuss some numerical considerations. First,
to avoid division by zero, Eq. 2 is set to zero when
the denominator is smaller than some ε > 0
5
. Sec-
ond, the derivatives are approximated by standard fi-
nite central differences. Due to the presence of noise,
estimating small values of curvatures is however a
delicate problem. Nevertheless, under the assump-
tion that the strands cannot mechanically bend over
some limit value, the finite differences are computed
using a grid spacing (denoted by ∆h) proportional to
the strand diameter S
dr
. A large value of ∆h allow
us to assess small curvature values despite the noise.
Also, we choose not to consider extremities of cen-
terlines. Finally, to yet increase the robustness, the
centerlines are first smoothed by a Gaussian filter of
standard deviation σ = 0.05 ×S
dr
.
4.3 Void Fraction
It is the ratio of area not occupied by the strands over
the area delimited by the inner part of the conduit.
A large void fraction means that strands are likely to
move and bend. Once the cables are segmented, it can
be obtained without difficulty.
4.4 Twist-pitch
The twist-pitch refers to the stranding periodicity of a
cable. Unlike the power cables or the Rutherford ca-
bles, the cables-in-conduit are wired and compacted
so that some (limited though) randomness is injected
in the architecture. As a consequence, the estima-
tion of twist-pitches only applies to cables-in-conduit.
Given the presence of some quantity of randomness,
we will estimate the twist-pitches using the autocor-
relation of the strand centerlines. Recall that differ-
ent stages are wired with different twist-pitches (see
Tab. 1). The estimation of these twist-pitches thus im-
plies to identify the stages of the cable.
The identification of the petals at different stages
can be seen as a hierarchical clustering problem, con-
strained by the pattern of the cable. To form clusters at
a given stage, a possible choice is to use pairwise dis-
tances of all strands. Indeed, closely running strands
are more likely to belong to the same petal.
5
ε is w.r.t. the precision of the implementation.
Let us formalize the above problem. We denote
the set of N centerlines of length K by {c
i
}
N
i=1
, where
c
i
∈ R
3K
. For any couple (i, j) ∈ {1,. ..,N}
2
, we de-
fine d(c
i
,c
j
) as the distances between c
i
and c
j
. The
distance is different depending of the norm. A rea-
sonable choice for d is the mean distance, based on
the L
2
norm. Additionally, for a given number of
stages (denoted by M), we denote by P
m
the num-
ber of petals, for any m ∈ {1,. ..,M}. We also de-
note by {ϕ
m
}
M
m=1
a set of applications where ϕ
m
:
{1,.. . ,N} → {1,.. . ,P
m
} assigns a label to each cen-
terline of the stage m, for any m ∈ {1,.. ., M}. Last,
we denote by 1
{.}
the indicator function returning 1 if
its argument is true, 0 otherwise. Then, we propose to
solve the constrained hierarchical clustering problem
by finding a minimizer to
M
∑
m=1
∑
(i, j)∈{1,...,N}
2
1
{ϕ
m
(i)=ϕ
m
( j)}
d(c
i
,c
j
)
2P
m
KM
, (3)
subject to the following constraints:
1. {ϕ
m
}
M
m=1
is a hierarchy,
2. For each petal at M = 1, N
sc
/N
nsc
are fixed,
3. For any stage, the size of each petal is fixed.
For a single stage, Eq. 3 can be put under the form
of an integer linear program (with a number of vari-
ables and constraints both of O(N
2
P
1
)) and solved
exactly using an integer linear programming solver.
For this experiment, the last version of CPLEX has
been chosen for its good performances (Mittelmann,
2007). Even for a simplistic situation where a sin-
gle stage and a limited number of centerlines are con-
sidered (N=15), several days of calculus are needed.
This remains acceptable for this setting but becomes
intractable for large cables with hundreds of strands.
To overcome this situation, we use a greedy strat-
egy for solving Eq. 3 heuristically. An illustrative ex-
ample is provided in Fig. 6 for the N05 cable (cluster-
ings are superimposed on source images). For the first
stage, random triplets satisfying the above second and
third constraints, are formed (see Fig. 6(a)). A greedy
heuristic is then applied, that consist in swapping the
pairs of centerlines satisfying the above second con-
straint and making the strongest decrease of Eq. 3.
This process is iterated until no swaps can be per-
formed (see Fig. 6(b)). The next stages are optimized
in the same way, except that (i) the initialization is
based on the clustering obtained at the previous stage
and (ii) that pairs of groups of centerlines are swapped
instead of centerlines (see Fig. 6(c,d)). This allows
us to keep clusterings as a hierarchy (first above con-
straint). Finally, the overall approach is run 100 times
and the solution having Eq. 3 minimum is kept.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
546

(a) (b) (c) (d)
Figure 6: Example of constrained hierarchical clustering for
identifying the the stages of the cable-in-conduit N05 at the
beginning (top row) and the end (bottom row). (a): initial-
ization of first stage, (b): result - first stage petals (triplets),
(c): initialization of second stage, (d): result - second stage
petals.
(a) (b) (c)
Figure 7: Toy example for estimating the area where a
strand section (S, red dot) can freely move with respect its
neighboring ones (T ). (b): complement of the morpholog-
ical closing of T by S, (c): geodesic reconstruction (light
gray) of S under (b).
4.5 Free Areas and Segments
Subject to an intense magnetic field, strands of cables-
in-conduit will transversally move wherever there
is locally an insufficient compaction. Identifying
these locations is therefore an important indicator of
fragility of some particular stranding pattern. For do-
ing so, we need a measure to estimate the area where
a strand can move. Let us denote by S ⊂ Z
2
the sec-
tion of a particular strand and by T that of the union
of the remaining ones, both from the same 2D binary
image taken along the z-axis (see Fig. 7(a)). We de-
note by F the area where S can move, obtained by
applying a morphological closing on T using S as a
structuring element (denoted by ϕ
S
(T), see Fig. 7(b))
and then performing a geodesic reconstruction of S
under the complement (denoted by (.)
c
) of ϕ
S
(T) (see
Fig. 7(c)):
F = [δ
B
(S) ∧[ϕ
S
(T)]
c
]
∞
,
where δ
B
(S) denotes the dilation of S by a ball B of
unit radius, ∧ denotes the logical AND and [.]
∞
de-
notes iterated until idempotence (achieved in practice,
in a finite number of iterations). Based on F, we pro-
pose a first possible descriptor, Free Transversal Area
(FTA), expressed as
FTA(F,S) =
](F \S)
]S
×100 ∈ R
+
.
The above descriptor is null when the strand cannot
move and increases as the strand gets a larger space to
move. The distribution of FTA is a descriptor reveal-
ing a fragility of a cable exposed to a strong magnetic
field. Extracting connected components where FTA
is greater than some positive value alongside a strand
permits to identify portions of strands able to move
transversally. This allows us to propose a second de-
scriptor of cable fragility, Free Transversal Segments
(FTS), defined as the set of all lengths of such seg-
ments.
5 EXPERIMENTAL RESULTS
5.1 Validation
5.1.1 Segmentation
Due to the variety of used cables and the variable
quality of images, the segmentation is a delicate task
needing validation. We propose to validate the results
by relying on an expert. First, this expert did a vi-
sual check of the segmented cables to ensure there
are no inconsistencies. Second, the contours of the
strands and the conduit (where applicable) have been
manually delineated by this expert on a few 2D im-
ages, equally spaced along the z-axis. For cables-in-
conduit and power cables, one image every 1.5mm
and 8.5mm has been selected, resp. Due to the va-
riety of resolution, three images have been only se-
lected per Rutherford cable.
To assess the accuracy of the results, we use eval-
uation metrics on the contours of strands and the con-
duit using the Volumetric Overlap Error (VOE), the
Relative Absolute Volume Difference (RAVD), the
Root Mean Square Distance (RMSD) and the Maxi-
mum Distance (MD) (see (Ginneken et al., 2007)) but
also the popular Dice Coefficient (Dice, 1945). Al-
though the metrics from (Ginneken et al., 2007) were
presented in a clinical setting, we do believe that they
still remain relevant here. In addition, we also pro-
pose to compare the position of centerlines using the
L
2
norm between centroids (CD).
The results of these comparisons are summarized
in Tab. 3. For each metric and type of cable, the mean
and standard deviation are provided. For cables-in-
conduit, the negative value of the mean RVD for s.c.
and n.s.c. strands indicates that their volume is under-
estimated and suggest an adjustment of segmentation
parameters. As expected, the error on n.s.c. strands
appears to be larger than of the s.c. ones due to their
poorly contrasted contours (e.g. a factor of two for the
mean CD). For most of the metrics used, compared to
Geometry Analysis of Superconducting Cables for the Optimization of Global Performances
547

N22 (96.42%) mgb2_133 (98.22%) 18PITN01 (95.46%)
N05 (95%) mgb2_113 (97.78%) 40RRPR01 (93.4%)
Figure 8: Accuracy of the segmentation procedures on the
contours strands and the conduit (if available). For each
type of cable, we select the 2D images from the obtained
segmentations and the manual ones with the same position
along the z-axis, having the mean largest (top row) and
smallest (bottom row) DC. Both images are combined to
show false negatives (red) and false positives (cyan), su-
perimposed on the corresponding source image. For each
image, the average DC is provided between parentheses.
other types of cables, the worst error is reached for
Rutherford cables. Nevertheless, all metrics globally
show that the structures of interest (especially the con-
duit) are well segmented with, for instance, a mean
DC greater than 94% and a mean RMSD always less
than 3 pixels. The position of centerlines is also well
preserved with a mean CD always less than 1.4 pixels.
A subset of these results is illustrated in Fig. 8. For
each type of cable, we provide the 2D images from
the obtained segmentations and the manual ones with
the same position along the z-axis (where manual seg-
mentations are available) having the largest (top row)
and the smallest (bottom row) average DC. Each cou-
ple of images is then combined to show false nega-
tives (red) / false positives (cyan), superimposed on
the source image.
5.1.2 Damage Indicators
To validate the capacity of the strand sections com-
pression indicators (see Section 4.1) to detect non-
circularities, we propose the following experiment
(see Fig. 9). Two distinct locations have been iden-
tified along the same strand of the N25 cable, where
the section is either ellipsoid or circular. It has been
verified that the compression is unique along the
strand. The contours of these sections superimposed
on source images are shown on top row. On the bot-
tom row are shown the response returned by the indi-
cators along the cable. Both EF and CMPN depict a
good robustness to noise and highlight well the com-
pression by reaching a large peak at the compressed
Figure 9: Validation of the strand section compression indi-
cators on the N25 cable. Orange and green triangles are
resp. normal and compressed locations along the same
strand. On top row, the sections contours are superimposed
on source images. Red circles are locations where partial
scans have been registered.
location and remaining close to zero or one elsewhere.
The same observations were made at other locations
and on Rutherford cables.
5.1.3 Clustering
Estimate the quality of the clustering w.r.t. ground
truths is an important issue. However, no ground
truths are currently available. Due to a large num-
ber of strands and an important number of constraints
to satisfy, their construction is indeed a difficult task,
especially when the cables are very short (as here).
Since the calculus of twist-pitches requires the cables
to be clustered, we believe that obtaining reasonable,
close-to-expected values, verifies the clusterings.
5.2 Results
5.2.1 Cables-in-conduit
First, we have compared the values of void fraction
obtained experimentally to nominal values. The re-
sult of these comparisons is presented in Tab. 4. In
average, the void fraction differs (in absolute value)
by 1.23% and does not exceed 2.72%. Compared to
the cable N05, it also confirms that the cables N22
and N25 are more likely do develop damages due to
larger void fraction.
Similarly, experimental values of twist-pitches
have been compared to nominal values. Depending of
the length of the sample, more than one or less than
one twisting periods can be available. For the studied
cables, an exhaustive comparison to references val-
ues is possible. The result of these comparisons is
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
548
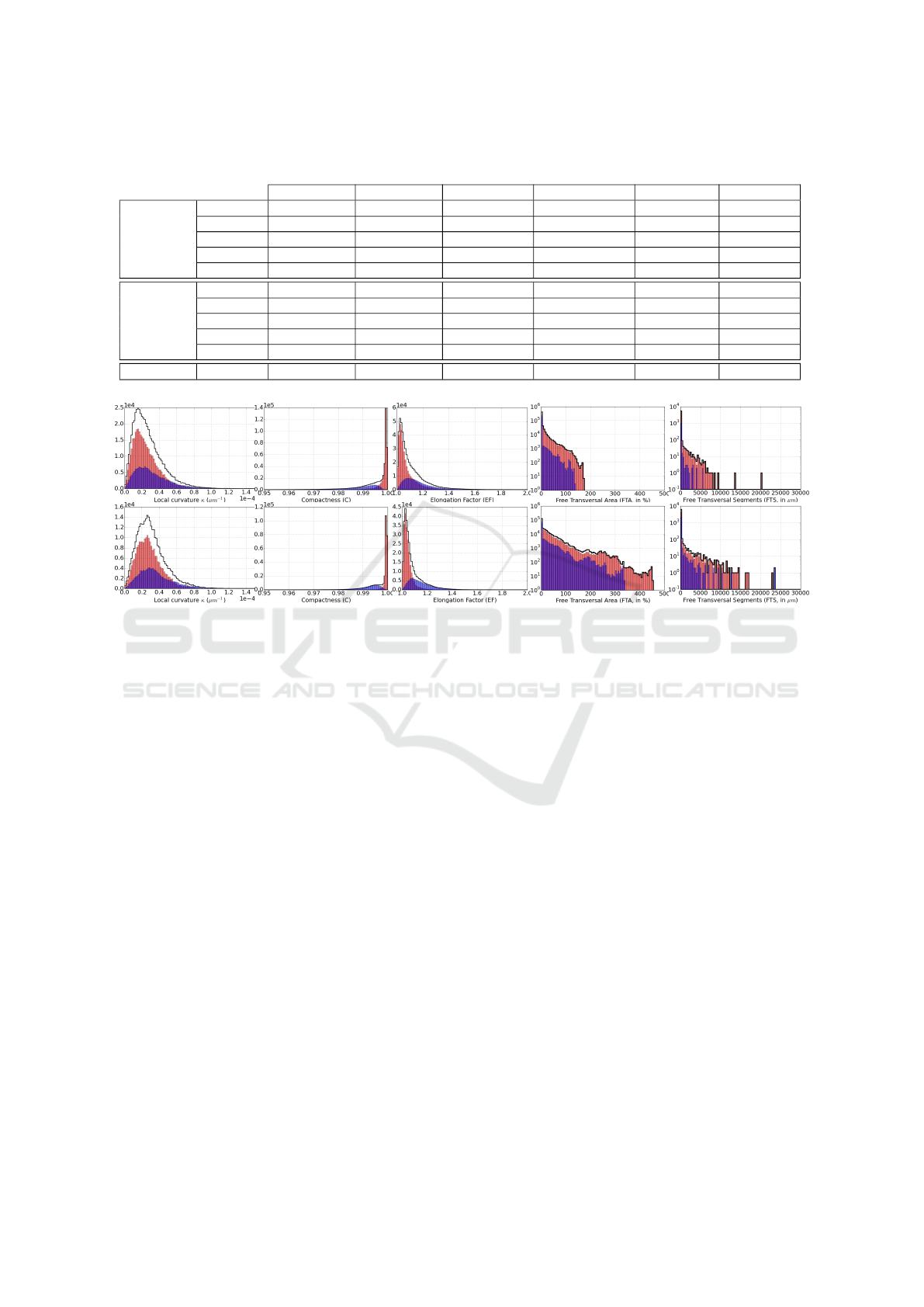
Table 3: Accuracy of the segmentation procedures with respect to ground truths for several metrics. The keyword "all" gathers
the contours of s.c. and n.s.c. strands as well as the contours of the conduit (if need be).
DC (%) VOE (%) RVD (%) RMSD (pixels) MD (pixels) CD (pixels)
In-conduit
s.c. 95.77 ±1.04 8.11 ±1.91 −7.47 ±2.17 1.60 ±0.28 3.73±0.97 0.59 ±0.36
n.s.c. 95.47 ±1.31 8.63 ±2.35 −3.04 ±2.89 1.85±0.41 5.04±1.63 1.22 ±0.84
s.c.+n.s.c. 95.63±1.18 8.35 ±2.14 −5.44 ±3.35 1.72±0.37 4.33±1.47 0.88 ±0.70
Conduit 99.67 ±0.06 0.67 ±0.12 −0.07 ±0.23 1.69±0.17 5.16±1.15 /
all 95.72 ±1.31 8.18 ±2.39 −5.33±3.41 1.71 ±0.36 4.34±1.47 /
Power
s.c. 97.86 ±0.51 4.18 ±0.97 1.06±1.69 1.62 ±0.21 4.54 ±1.03 0.86 ±0.48
n.s.c. 97.99 ±0.44 3.93 ±0.84 −0.87 ±1.53 1.57±0.23 4.27±1.02 0.83 ±0.43
s.c.+n.s.c. 97.94±0.47 4.03 ±0.90 −0.11 ±1.85 1.59±0.22 4.38±1.03 0.84 ±0.45
Conduit 99.80 ±0.10 0.39 ±0.20 0.38±0.22 2.10 ±0.35 7.06±3.43 /
all 97.97 ±0.52 3.97 ±1.01 −0.10±1.84 1.60 ±0.23 4.42±1.16 /
Rutherford s.c. 94.44 ±1.19 10.52 ±2.13 −0.99 ±3.10 2.45 ±0.74 6.49 ±2.56 1.39 ±1.05
(a) (b) (c) (d) (e)
Figure 10: Distributions of damage indicators for s.c. (pink), n.s.c. (blue) and both (black thick line) strands along the
cables-in-conduit N05 (top row) and N25 (bottom row). The y-axis of FTA and FTS is in log-scale.
shown in Tab. 5. In average, the twist-pitches dif-
fer (in absolute value) by 2.93mm (3.25%) and do
not exceed 9.38mm (7.5%). Despite the randomness
injected in these cables, this result demonstrates that
twist-pitches remain close to nominal values.
Additionally, we have computed the correlations
between local curvature and strand sections compres-
sion indicators. Then, we have decided to retain the
most relevant couples of indicators for which the ab-
solute value of the correlation coefficient is larger than
0.8. Not surprisingly, EF and CMPN are well cor-
related. But most importantly, no correlation have
been identified between locally elevated curvature and
other indicators, meaning that bendings and compres-
sions locations do not coincide.
Moreover, we have compared in Fig. 10 the distri-
butions of several damage indicators (local curvature,
CMPN, EF, FTA and FTS) of two cables-in-conduit
that present different lengths, void fractions and twist-
pitches: N05 (top row) and N25 (bottom row). The
distribution of FTS is obtained by thresholding FTA at
15%, which appears to be a good value to keep signif-
icant transversal moves. For each image, we provide
both the distribution over s.c. (pink), n.s.c. (blue) and
both (black thick line) strands. For both cables, local
curvatures remain very small due to the near linearity
of strands. Also, the shape of the related distribution
suggests that it is centered around the curvature in-
duced by the twist-pitch and that local curvature max-
ima correspond to locations of potential conductivity
loss. The mean of these distributions is nearly the
same (2 ×10
−5
µm
−1
) corresponding to a curvature
radius of 50mm. Nevertheless, the mean is slightly
larger for the N25 cable. This is consistent with the
fact that this cable has smaller twist-pitch values. Ad-
ditionally, the distribution of EF and CMPN on both
cables is centered, as expected, on a value close to
one, meaning that strands sections are mainly circular.
The higher peak and longer tail of the EF distribution
on s.c. strands for N05 than for N25 indicates more
frequent and more heavily compressed strands. This
is expected as a consequence of stronger compaction
of the N05 cable.
Finally, the tail of the FTA and FTS distributions
of the N05 cable is shorter than for the N25 cable.
This means that the strands of the N05 cable have
much less space to move and that the segments where
they can move are shorter. These distributions tend
to decrease, meaning that a large area where a strand
can move is less likely to occur in the cable than a
Geometry Analysis of Superconducting Cables for the Optimization of Global Performances
549
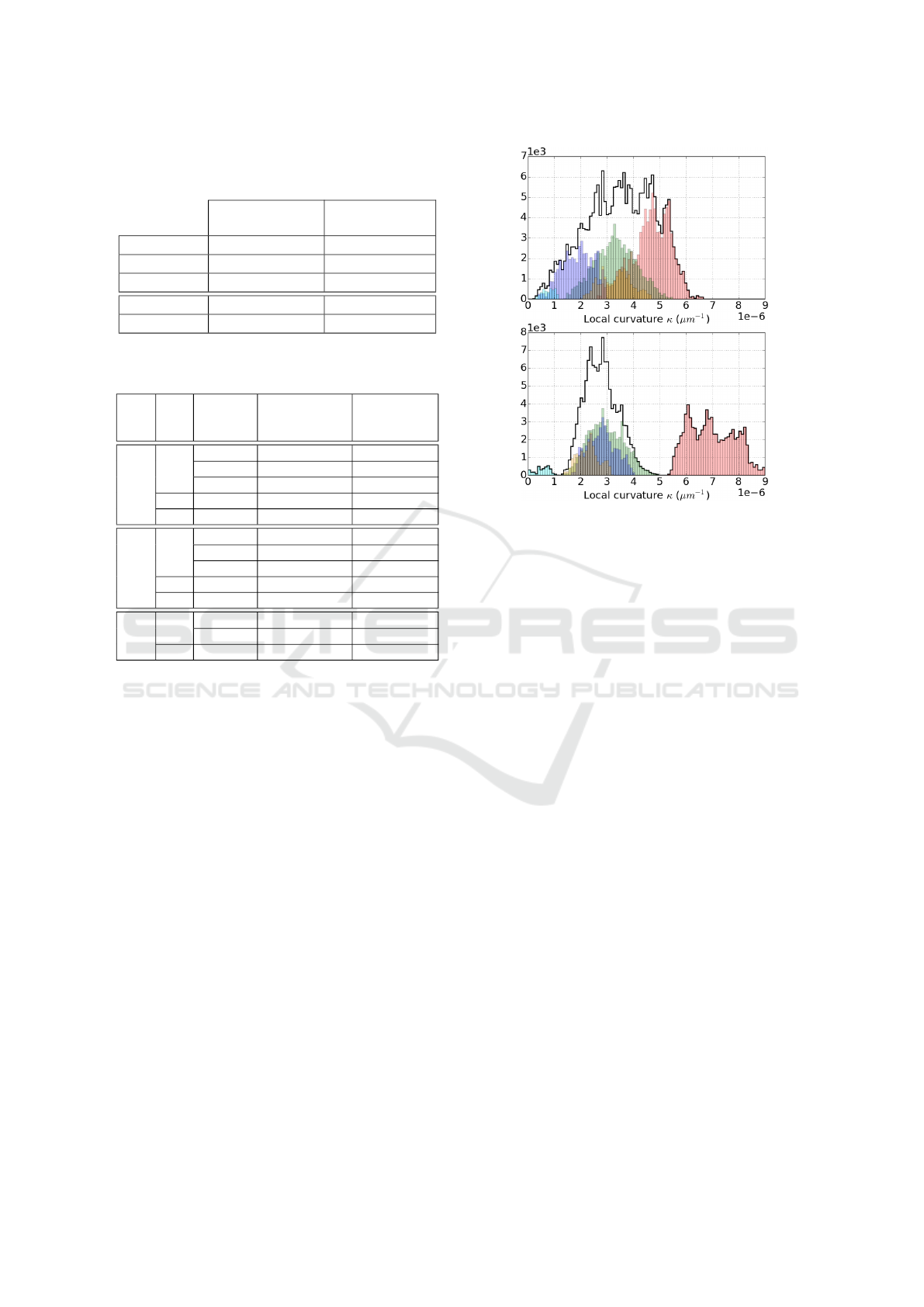
Table 4: Comparison of experimental and nominal values
of void fraction for all cables-in-conduit (top) and all power
cables (bottom).
Measured void
fraction (%)
Nominal void
fraction (%)
N05 24.16 ±0.19 25%
N22 30.28 ±0.16 33%
N25 33.13 ±0.14 33%
mgb2_113 27.57 ±0.38 24.7%
mgb2_133 27.09 ±0.41 24.7%
Table 5: Comparison of experimental and nominal values
of twist-pitches for all cables-in-conduit.
Cable Stage
Twisting
Period
Experimental
twist-pitches
(mm)
Nominal
twist-pitches
(mm)
N05
1
1 43.81 ±1.46 45
2 87.95 ±2.52 90
3 131.57 ±5.89 135
2
1 83.10 ±6.00 85
3
1 129.06 ±0.00 125
N22
1
1 43.92 ±1.26 45
2 87.82 ±2.24 90
3 131.77 ±3.63 135
2
1 82.22 ±2.80 85
3
1 115.62 ±0.00 125
N25
1
1 35.84 ±1.13 35
2 72.93 ±2.48 70
2
1 61.89 ±1.49 65
small one. Again, this is an expected consequence of
the stronger compaction of the N05 cable. Moreover,
large areas are more likely to occur for s.c. strands
than for n.s.c. strands. This is consistent with the fact
that the number s.c. strands is greater than the number
of n.s.c. strands (see Table 1).
5.2.2 Power Cables
As for cables-in-conduit, the values of void fraction
obtained experimentally from segmentations have
been first compared to nominal values. The result of
these comparisons is available in Tab. 4. In average,
the void fraction differs (in absolute value) by 2.6%
from the nominal values and does not exceed 2.87%
(which appears to be slightly larger than for cables-
in-conduit).
Finally, we have compared in Fig. 11 the distribu-
tions of the local curvature of the two power cables:
mgb2_113 and mgb2_133. As for cables-in-conduit,
the strands have near linear trajectories, thus leading
to small values of local curvature up to 9×10
−6
µm
−1
.
This corresponds to a maximum radius of curvature
of 111mm. Unlike cables-in-conduit, the shape of the
related distributions is multimodal where each mode
Figure 11: Distributions of the local curvature κ along the
power cables mgb2_113 (top) and mgb2_133 (bottom) for
s.c. strands (pink), n.s.c. strands (green, blue, orange, cyan,
resp. from outer to inner stages) and all strands (black thick
line).
is centered on the local curvature of the correspond-
ing concentric layer of strands. Each mode appears to
be well separated from the others. Whereas we expect
to get an increasing local curvature as the concentric
layer becomes large, it seems to be only partially true.
A possible explanation is the existence of slightly dif-
ferent twist-pitches among these layers.
5.2.3 Rutherford Cables
In Fig. 12, we have compared the distributions of
several damage indicators (local curvature, CMPN
and EF) of two Rutherford cables presenting a dif-
ferent length and number of strands: 18RRPN01 and
40RRPR02. Notice that the y-axis of all images is in
log-scale to ease the analysis of results. In contrast to
the other types of cables studied, the local curvature
appears to be much larger (due to the folding of the
cable), up to 2.75 ×10
−4
µm
−1
. This corresponds to
a radius of curvature of 3.63mm. Moreover, the dis-
tribution of all indicators share the same shape. More
precisely, the head of these distributions corresponds
to the circular and straight strands with null values of
local curvature and values close to one for the other
indicators. The tail of these distributions corresponds
to compressed and curved strands, on the sides of the
cable.
Finally, the correlations between all the above in-
dicators have been computed. The most relevant cou-
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
550

Figure 12: Distributions of the local curvature (top row),
CMPN (middle row) and the elongation factor (bottom row)
along the Rutherford cables 18RRPN01 and 40RRPR02.
For the purpose of visualization, the y-axis of all images
is in log-scale.
ples of indicators were selected as those having an ab-
solute correlation coefficient above 0.8. These corre-
lations have permitted to conclude that EF and CMPN
are the most correlated ones. The obtained corre-
lations between local curvature and strand sections
compression indicators also confirmed that bendings
and compressions locations coincide quite well with
a coefficient of about 0.7 in absolute value.
6 CONCLUSION
This paper presents a segmentation and geometry
analysis of three types of cables and is, to our knowl-
edge, the first one to provide methods and results to
this aim. The segmentation results exhibit a good ac-
curacy w.r.t. manually provided ground truth. The
features appear to be relevant for detecting deforma-
tions such as crushing or bending. The results are now
going to be analyzed. We have found, for instance,
that s.c. and n.s.c. strands exhibit different distribu-
tions of the crushing-related features. Similarly, no
spatial correlation between crushing and bending was
found. A further statistical analysis of the results will
be done in the future.
REFERENCES
Dice, L. (1945). Measures of the amount of ecologic asso-
ciation between species. 26(3):297–302.
Ginneken, B., Heimann, T., and Styner, M. (2007). 3D seg-
mentation in the clinic: A grand challenge.
IEC (2004). Âmes des câbles isolés. IEC Central Office
Geneva Switzerland. CEI 60228:2004.
Ikonen, L. (2005). Pixel queue algorithm for geodesic dis-
tance transforms. 3429:228–239.
Manil, P., Mouzouri, M., and Nunio, F. (2012). Mechanical
modeling of low temperature superconducting cables
at the strand level. 22(3).
Meyer, F. (1991). Un algorithme optimal de ligne de partage
des eaux. volume 2, pages 847–859.
Milanese, A., Devaux, M., Durante, M., Manil, P., Perez, J.,
Rifflet, J., De Rijk, G., and Rondeaux, F. (2012). De-
sign of the EuCARD high field model dipole magnet
FRESCA2. 22(3).
Mittelmann, H. (2007). Recent benchmarks of optimization
software.
Montero, R. (2009). State of the art of compactness and
circularity measures. 4(27):1305–1335.
Oberli, L. (2013). Development of the Nb
3
Sn Ruther-
ford cable for the EuCARD high field dipole magnet
FRESCA2. 23(3).
Seidel, M. and Sturge, D. (2009). Tensile surface and struc-
ture: A pratical guide to cable and membrane con-
struction. Wiley.
Sternberg, R. (1986). Grayscale morphology. 35(3):333–
355.
Torre, A., Bajas, H., and Ciazynski, D. (2014). Mechani-
cal and electrical modeling of strands in two ITER CS
cable designs. 24(3).
Žuni
´
c, J. (2012). Shape descriptors for image analysis.
15(23):5–38.
Weiss, K., Heller, R., Fietz, W., Duchateau, J., Dolgetta, N.,
and Vostner, A. (2007). Systematic approach to ex-
amine the strain effect on the critical current of Nb
3
Sn
cable-in-conduit-conductors. 17(2):1469–1472.
Geometry Analysis of Superconducting Cables for the Optimization of Global Performances
551
