
Hessian Eigenfunctions for Triangular Mesh Parameterization
Daniel Mejia, Oscar Ruiz-Salguero and Carlos A. Cadavid
Laboratorio de CAD CAM CAE, Universidad EAFIT, Cra 49 No-7 Sur-50, 050022, Medellin, Colombia
Keywords:
Applied Differential Geometry, Dimensionality Reduction, Hessian Locally Linear Embedding, Manifold
Learning, Mesh Parameterization.
Abstract:
Hessian Locally Linear Embedding (HLLE) is an algorithm that computes the nullspace of a Hessian func-
tional H for Dimensionality Reduction (DR) of a sampled manifold M. This article presents a variation of
classic HLLE for parameterization of 3D triangular meshes. Contrary to classic HLLE which estimates local
Hessian nullspaces, the proposed approach follows intuitive ideas from Differential Geometry where the local
Hessian is estimated by quadratic interpolation and a partition of unity is used to join all neighborhoods. In
addition, local average triangle normals are used to estimate the tangent plane T
x
M at x ∈ M instead of PCA,
resulting in local parameterizations which reflect better the geometry of the surface and perform better when
the mesh presents sharp features. A high frequency dataset (Brain) is used to test our algorithm resulting in a
higher rate of success (96.63%) compared to classic HLLE (76.4%).
1 INTRODUCTION
Dimensionality Reduction (DR) takes a d-manifold
M ⊂ R
D
and computes a map h : M → R
d
such that: 1)
h is bijective and 2) h and h
−1
are continuous. There-
fore, h is an homeomorphism and the image of M un-
der h is a DR of M.
Mesh Parameterization can be seen as a particular
case of DR where M ⊂ R
3
is a triangular mesh of a
2-manifold (i.e. D = 3 and d = 2). Triangular meshes
are very common data structures in CAD CAM CAE
applications and parameterization of such meshes is
relevant for areas such as: reverse engineering, tool
path planning, feature detection, etc.
A natural way to handle Mesh Parameterization is
to attack the problem from the point of view of DR.
Classic HLLE (Hessian Locally Linear Embedding)
(Donoho and Grimes, 2003) is an algorithm which
proposes to compute a DR of M by computing the
eigenvectors of a Hessian functional. This article pro-
poses a modification for the classic HLLE which can
be applied to triangular meshes. Our proposed ap-
proach computes a partition of unity on M and esti-
mates the tangent Hessian on each neighborhood N
i
of
M by interpolating any function f with second degree
polynomials. In addition, local average triangle nor-
mals are used to compute the tangent local plane T
x
M
of M which is more consistent than Principal Compo-
nent Analysis (PCA) specially for surfaces with sharp
features.
The remainder of this article is organized as fol-
lows: Section 2 reviews the relevant literature. Sec-
tion 3 describes the implemented methodology. Sec-
tion 4 discusses and compares the results of the pro-
posed approach against classic HLLE. Section 5 con-
cludes the paper and introduces what remains for fu-
ture work.
2 LITERATURE REVIEW
Given a set of points X = [x
1
,x
2
,...,x
n
] ⊂ R
D
ly-
ing on a d-manifold M, DR seeks a homeomorphic
function h : M → R
d
such that the set of points
[h(x
1
),h(x
2
),...,h(x
n
)] ⊂ R
d
compose a DR of X.
For the rest of the article we assume D = 3 and d = 2,
turning the DR problem into a Mesh Parameterization
one.
The most popular algorithm for DR is the Princi-
pal Component Analysis (PCA). PCA is a linear al-
gorithm which parameterizes M by projecting X onto
a plane, which is only a valid parameterization if h is
linear. However, this assumption limits the algorithm
making it useful only for trivial cases.
For nonlinear manifolds, other approaches have
been proposed in the literature. For example, Isomap
(Tenenbaum et al., 2000) attempts to compute an
isometric parameterization of M by computing the
geodesic distances in M and reproducing them in the
Mejia, D., Ruiz-Salguero, O. and Cadavid, C.
Hessian Eigenfunctions for Triangular Mesh Parameterization.
DOI: 10.5220/0005668200730080
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 75-82
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
75

parameter space. Isomap has been succesfully ap-
plied in the context of Mesh Parameterization (Sun
and Hancock, 2008; Ruiz et al., 2015). Usually a
shortest path algorithm such as Dijktra’s or Floyd’s
is used to estimate geodesic distances which fail for
non-convex manifolds such as surfaces with holes.
Spectral theory is an important branch of graph
theory where several DR algorithms have been de-
rived. Laplacian Eigenmaps (Belkin and Niyogi,
2003) computes the Laplacian matrix which acts over
any function defined on the graph of M measur-
ing its curvature. Diffusion Maps (DM) (Lafon and
Lee, 2006) computes the Markov matrix which esti-
mates the transition probability between vertices of
the graph of M. DR is achieved in both cases by com-
puting the eigenvectors of these matrices respectively.
Spectral algorithms preserve topologic properties of
the underlying graph keeping adjacent points near in
the parameter space. However, these algorithms usu-
ally fail to preserve geometric properties which be-
comes important in Mesh Parameterization applica-
tions.
Other DR algorithms focus on a more local ap-
proach where each neighborhood is first parame-
terized locally and then all the neighborhoods are
aligned in the parameter space trying to preserve ge-
ometric properties. Locally Linear Embedding (LLE)
(Roweis and Saul, 2000) expresses each point in M
as a linear combination of its neighborhs and then
computes the DR attempting to preserve such struc-
ture in the parameter space for all the points. Simi-
larly, Local Tangent Space Alignment (LTSA) (Zhang
and Zha, 2002) projects each neighborhood onto the
tangent plane via PCA and then attempts to align
all the neighborhoods in the parameter space using
rigid transformations. These algorithms highly pre-
serve geometric properties and perform well for non-
convex manifolds. However, they expect that each
neighborhood lies on a linear subspace which fails at
sharp features of 3D meshes resulting in non-bijective
parameterizations. Most Mesh Parameterization al-
gorithms also follow this idea by aligning triangles in
the parameter space preserving geometric properties
for each triangle (L
´
evy et al., 2002; Liu et al., 2008;
Athanasiadis et al., 2013; Smith and Schaefer, 2015)
or as LLE does, by locally convex linear combinations
(Floater, 1997; Lee et al., 2002). Other Mesh Param-
eterization algorithms compute the resulting parame-
terization in terms of the angles of the Mesh (Sheffer
and de Sturler, 2001; Kharevych et al., 2006; Zayer
et al., 2007).
2.1 Classic Hessian Locally Linear
Embedding (HLLE)
Classic Hessian Locally Linear Embedding (Donoho
and Grimes, 2003) is a DR algorithm which com-
bines ideas from LLE and LTSA with ideas from di-
crete differential geometry. HLLE computes a local
parameterization of each neighborhood using PCA.
But instead of aligning all neighborhoods by a rigid
mapping, HLLE estimates a Hessian functional H on
M (similar to Laplacian Eigenmaps which estimates a
Laplacian functional) and computes the DR of M by
estimating the kernel of H , i.e. ker(H ) = { f |H f =
0}.
In order to compute H , the tangent Hessian H
tan
x
must be defined (Donoho and Grimes, 2003):
H
tan
x
f =
∂
2
f
∂b
2
1
∂
2
f
∂b
1
∂b
2
∂
2
f
∂b
2
∂b
1
∂
2
f
∂b
2
2
, (1)
where b
1
,b
2
∈ R
3
is an orthonormal basis for the
tangent plane T
x
M at x. If f = { f
1
, f
2
,..., f
n
} with
f
i
= f (x
i
) is the function f restricted to the set of
points X, then the Hessian functional H is defined
as (Donoho and Grimes, 2003):
H f =
Z
M
kH
tan
x
f k
2
F
dA =
n
∑
i=1
Z
M
i
φ
i
kH
tan
x
f k
2
F
dA
≈ f
T
Kf (2)
where f ∈ C
2
(M) is a smooth function defined on
M, k · k
F
is the Frobenius norm, dA is a surface dif-
ferential, (M
i
, φ
i
) is a partition of unity of M and
K = (K
1
+K
2
,...,K
n
) is the discrete Hessian estima-
tor computed by adding each local Hessian estimator
K
i
at each neighborhood N
i
.
Since the matrix K approximates the Hessian
functional on M, the kernel of H can be estimated by
solving the following minimization problem (Donoho
and Grimes, 2003):
h
1
= arg min
f
f
T
Kf, h
2
= arg min
f
f
T
Kf
s.t.
kh
i
k = 1, h
i
⊥ 1, h
1
⊥ h
2
,
i = 1, 2
(3)
where h
1
= [h
1
(x
1
),...,h
1
(x
n
)]
T
and h
2
=
[h
2
(x
1
),...,h
2
(x
n
)]
T
are the respective coordi-
nates of X in the parameter space. The constant
function f (x) = c, c ∈ R, is in the kernel of H (the
Hessian of any constant function is 0 as per eq. (1)).
Therefore, the constraint h
i
⊥ 1 avoids collapsing
all the vertices to a single point. The constraint
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
76

h
1
⊥ h
2
guarantees linear independence which avoids
collapsing the surface into a line. The constraint
kh
i
k = 1 fixes the scale of the solution.
Eq. (3) can be solved by computing the eigenvec-
tors of K associated to the second and third lowest
eigenvalue (the eigenvector associated to the lowest
eigenvalue corresponds to the constant function 1).
Basically, classic HLLE algorithm consists of: 1)
estimate the local Hessian functionals K
1
,K
2
...,K
n
and the Hessian functional K = K
1
+ K
2
+ ··· + K
n
and 2) compute the eigenvectors of K with the small-
est eigenvalue (Donoho and Grimes, 2003).
Like LLE and LTSA, classic HLLE may present
problems for datasets with sharp features resulting in
non-bijective mappings. In addition, the computation
of the matrix K
i
which estimates the local Hessian
functional H |
i
is not consistent with the definition in
eq. (2) as only Hessian nullspaces are computed.
Conclusions of the Literature Review. In Mesh Pa-
rameterization applications, the preservation of geo-
metric properties is a priority over topology preser-
vation. Algorithms such as Laplacian Eigenmaps
and DM present highly distorted parameterizations.
Therefore, algorithms that preserve geometric prop-
erties such as Isomap, LLE, LTSA and classic HLLE
are more effective. However, these algorithms present
drawbacks such as the inability to work with con-
vex datasets or high frequency datasets, which are
very common in engineering applications. Mesh Pa-
rameterization algorithms do not face such problems.
However they are only restricted to triangular meshes.
To partially overcome these problems, this arti-
cle proposes a variation of the classic HLLE algo-
rithm for parameterization of triangular meshes. Clas-
sic HLLE algorithm is selected for this purpose since
such algorithm has provided better experimental re-
sults for Mesh Parameterization than other DR algo-
rithms (Ruiz et al., 2015). Also, since HLLE is a DR
algorithm, the proposed approach can be easily ex-
tended to meshes composed of non-triangular faces
posing a potential advantage over traditional Mesh
Parameterization algorithms.
3 METHODOLOGY
In order to parameterize M, we propose to follow the
same idea of the classic HLLE which is described in
section 2.1 (Donoho and Grimes, 2003): 1) estimate
the tangent Hessian H
tan
x
and the Hessian functional
K
i
at each N
i
, 2) estimate the Hessian functional H on
M as per eq. (2) and 3) estimate the kernel of H for
Mesh Parameterization via eigendecomposition. The
algorithm is briefly described below:
1. For each neighborhood estimate the tangent plane
T
x
M at x
i
by computing the local average normal
vector
n
i
and compute a local parameterization O
i
by projecting N
i
onto T
x
M.
2. Estimate the tangent Hessian H
tan
x
f and kH
tan
x
f k
2
F
at x
i
by quadratic interpolation.
3. Apply the partition of unity φ
i
to estimate the local
Hessian functional
R
M
i
φ
i
kH
tan
x
k
2
F
dA ≈ f
T
K
i
f.
4. Estimate the global Hessian functional H ≈ K =
∑
n
i=1
K
i
.
5. Compute two orthogonal functions h
1
and h
2
which solve the optimization problem posed in eq.
(3) by eigendecomposition of the matrix K.
The steps of the algorithm are detailed below.
3.1 Tangent Plane T
x
M and Local
Parameterization O
i
In order to estimate the tangent Hessian H
tan
x
at x
i
,
the tangent plane T
x
M at x
i
is estimated. Classic
HLLE estimates T
x
M applying PCA on N
i
. However,
we propose to estimate T
x
M using the information of
the triangulation T as follows: let {t
i
1
,t
i
2
,...} and
{n
i
1
,n
i
2
,...} be the set of triangles adjacent to x
i
and
their corresponding normal vectors respectively. Set
T
x
M as the plane with origin x
i
and normal n
i
(where
n
i
is the average of {n
i
1
,n
i
2
,...}). Finally, O
i
is com-
puted by projecting N
i
onto T
x
M.
Using the local average adjacent normals to com-
pute T
x
M usually results in better approximations of
the tangent plane than PCA and if N
i
belongs to a
sharp region, PCA may fail to recover a bijective pa-
rameterization while the local average normals pa-
rameterization has a better chance of being bijec-
tive. These local parameterizations affect the result-
ing global parameterization in the sense that local
non-bijectivity results in a folding of the surface in
the global parameterization.
3.2 Tangent Hessian H
tan
x
f and
kH
tan
x
f k
2
F
The definition of tangent Hessian in eq. (1) requires
a smooth function defined on M. Quadratic inter-
polation is used in order to estimate such Hessian
in a discrete surface. Let [b
1
,b
2
] be an orthonor-
mal basis of T
x
M at x
i
. Therefore, any point p on
T
x
M at x
i
can be expressed as p = ub
1
+ vb
2
+ x
i
.
Let {u
i
1
,u
i
2
,...,u
i
k
} and {v
i
1
,v
i
2
,...,v
i
k
} be the cor-
responding coordinates of O
i
in this basis. If f
i
=
Hessian Eigenfunctions for Triangular Mesh Parameterization
77
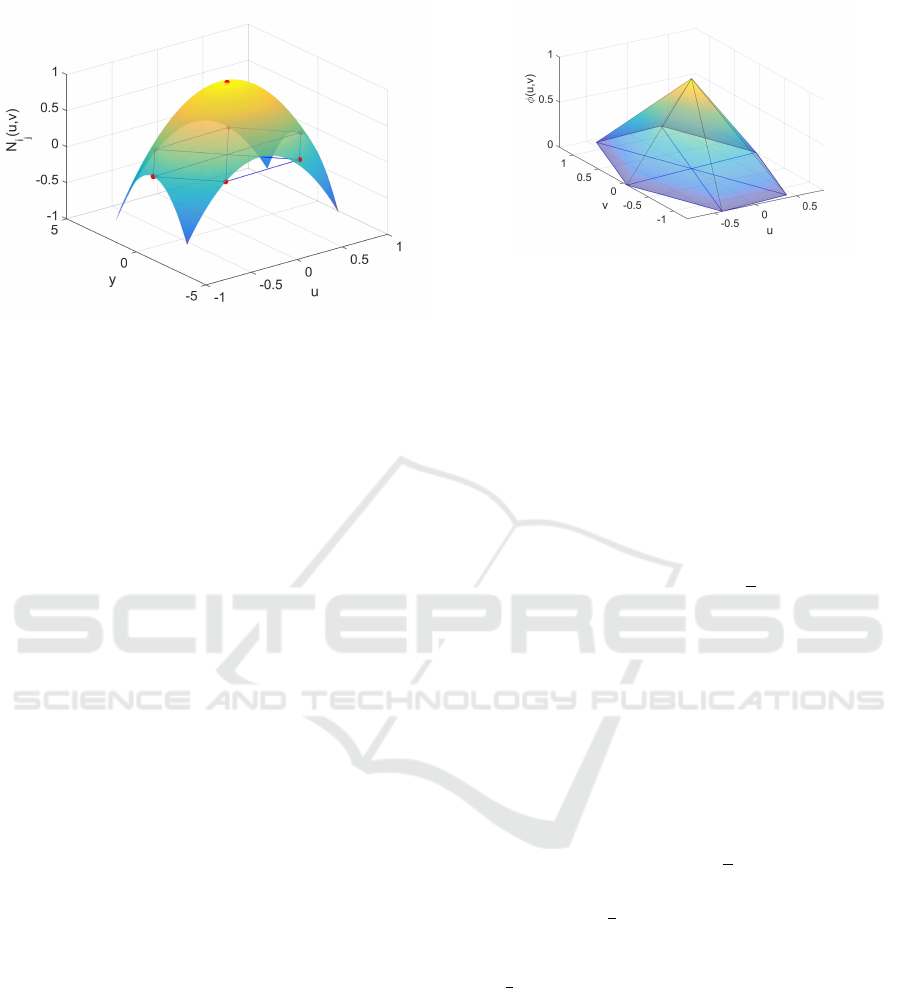
Figure 1: Quadratic interpolation function N
i
j
at N
i
such
that N
i
j
(x
i
k
) = 1 if j = k, 0 otherwise.
{ f
i
1
, f
i
2
,..., f
i
k
} are the values of f restricted to N
i
,
then f can be interpolated at T
x
M by a second order
polynomial as follows:
f (u,v) =
k
∑
j=1
N
i
j
(u,v) f
i
j
, (4)
with N
i
j
(u,v) = α
j
u
2
+ β
j
uv + γ
j
v
2
+ δ
j
u + ε
j
v + ζ
j
.
Since f (u
j
,v
j
) = f
i
j
, the interpolation functions N
i
j
are required to satisfy N
i
j
(u
i
l
,v
i
l
) = 1 if j = l and
N
i
j
(u
i
l
,v
i
l
) = 0 if j 6= l (fig. 1). The coefficients of
N
i
j
are computed by solving the arising linear sys-
tem of equations in a least squares sense. Afterwards,
equation (1) can be approximated as:
H
tan
x
f ≈
2α
α
α
T
i
f
i
β
β
β
T
i
f
i
β
β
β
T
i
f
i
2γ
γ
γ
T
i
f
i
, (5)
where α
α
α
i
, β
β
β
i
and γ
γ
γ
i
are column vectors with the cor-
responding coefficients of the quadratic terms in eq.
(4). Therefore, the norm of the tangent Hessian can
be estimated as kH
tan
x
f k
2
F
≈ f
T
i
C
i
f
i
, where C
i
is a sym-
metric matrix defined as:
C
i
= 4α
α
α
i
α
α
α
T
i
+ 2β
β
β
i
β
β
β
T
i
+ 4γ
γ
γ
i
γ
γ
γ
T
i
(6)
3.3 Partition of Unity φ
φ
φ and Local
Hessian Functional K
i
Eq. (2) requires a partition of unity (M
i
,φ
i
) defined
on M. A partition of unity φ
φ
φ =
{
φ
1
,φ
2
,...,φ
n
}
is a set
of functions satisfying the following properties:
1. M
i
is an open subset of M.
2.
S
n
i=1
M
i
= M.
3. φ
i
: M → [0,1].
4. φ
i
(x) = 0 if x /∈ M
i
.
Figure 2: Partition of unity φ
i
for a selected neighborhood
N
i
. φ
i
equals to 1 at x
i
and vanishes to 0 at adjacent points.
5.
∑
n
i=1
φ
i
(x) = 1 for all x ∈ M.
A partition of unity for M can be build as a set
of piecewise linear functions such that for N
i
, φ
i
is
defined as:
φ
i
(x
j
) =
(
1 if i = j
0 otherwise
, ∀ j = 1,2,...,n. (7)
By its definition in eq. (7), φ
i
vanishes at other
neighborhoods. Therefore:
Z
M
φ
i
dA =
Z
M
i
φ
i
dA =
1
3
∑
j
A
i
j
, (8)
where A
i
j
is the area of the j-th adjacent triangle of
x
i
. It is not hard to check that eq. (7) satisfies the
properties of a partition of unity if M is a triangular
mesh.
Finally, from eqs. (6) and (8) the local Hessian
functional in eq. (2) can be estimated:
Z
M
i
φ
i
kH
tan
x
f k
2
F
dA ≈
Z
M
i
φ
i
dA
f
T
i
C
i
f
i
=
1
3
∑
j
A
i
j
!
f
T
i
C
i
f
i
. (9)
The matrix
1
3
∑
j
A
i
j
C
i
estimates the local Hes-
sian functional for any f
i
. Therefore, the matrix K
i
is
built as an n×n symmetric matrix which has the terms
of
1
3
∑
j
A
i
j
C
i
at the indices dictated by (N
i
,N
i
), and
zeros elsewhere.
3.4 Global Hessian H and
Parameterization of M
The Hessian functional is estimated exactly as de-
scribed in (Donoho and Grimes, 2003) by adding each
local Hessian: H ≈ K =
∑
i
K
i
. Finally, the parame-
terization h
1
, h
2
of M is achieved by solving the min-
imization problem in eq. (3) via eigendecomposition
of the matrix K.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
78
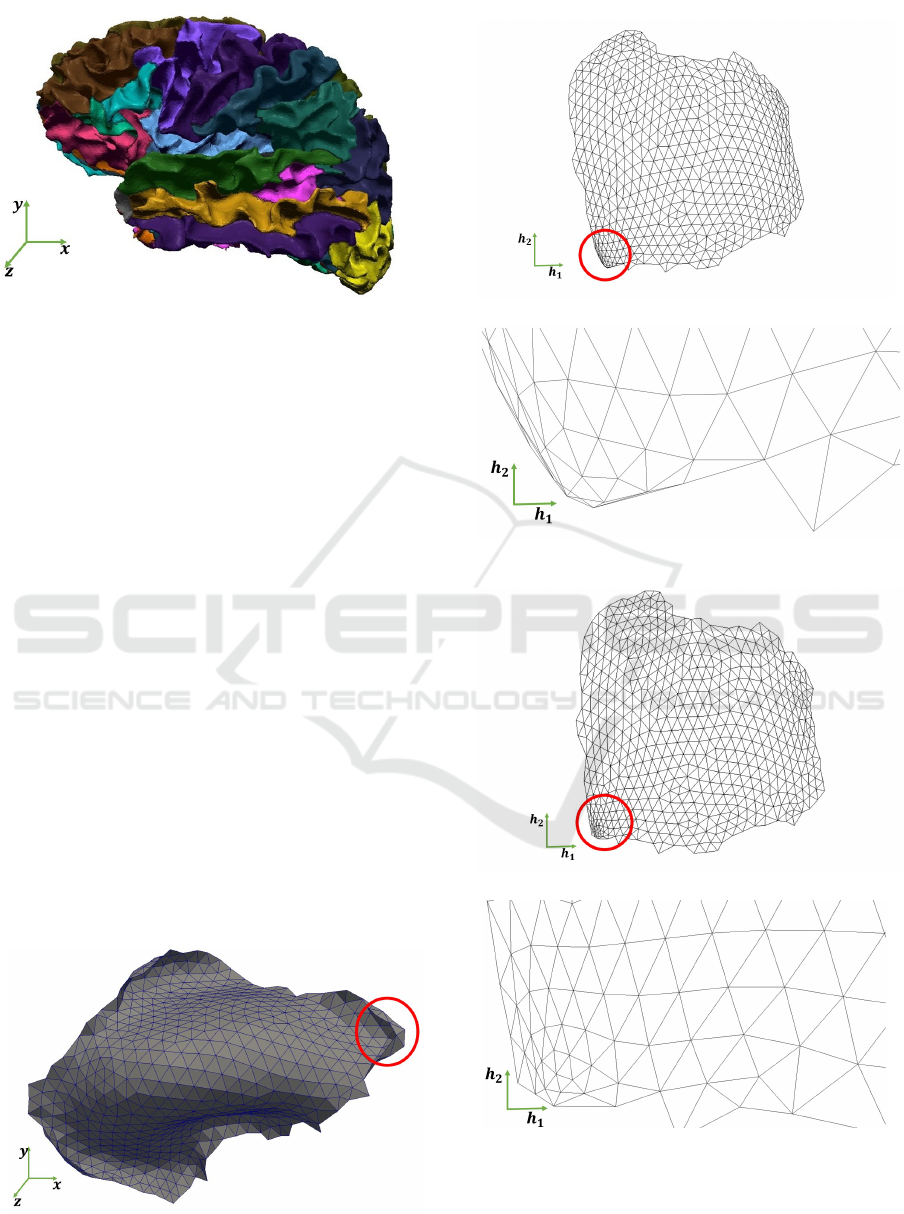
Figure 3: Segmented Brain dataset.
4 RESULTS AND DISCUSSION
In this section we present and discuss the parame-
terization results obtained for the segmented Brain
dataset (Desikan et al., 2006) and the Face dataset
(Ruiz et al., 2015). We also present an asymptotic
time complexity comparison for our algorithm and
several Mesh Parameterization algorithms.
4.1 Datasets
The Brain dataset (fig. 3) presents several challenges
in terms of Mesh Parameterization given the high cur-
vatures and the low developability of the surface. We
remeshed all the sub-meshes and some of them were
also partitioned manually prior to parameterization.
From the 89 sub-meshes, classic HLLE computed
only 68 (76.40%) bijective parameterizations while
our algorithm computed 86 (96.63%) bijective map-
pings.
The Left Hemisphere - Frontal Pole sub-mesh (fig.
4) presents a high frequency zone near a corner. Fig. 5
presents the parameterization results obtained by clas-
Figure 4: Left Hemisphere - Frontal Pole mesh. The red
ellipse marks a high frequency zone.
(a) Non-bijective parameterization with classic HLLE.
(b) Zoom into high frequency zone for classic HLLE (non-
bijective).
(c) Bijective parameterization with our algorithm.
(d) Zoom into high frequency zone for our algorithm (bi-
jective).
Figure 5: Parameterization results for the Left Hemisphere
- Frontal Pole mesh. The red ellipse marks the high fre-
quency zone.
Hessian Eigenfunctions for Triangular Mesh Parameterization
79

(a) Left Hemisphere - Rostral Anterior Cingulate mesh.
(b) Non-bijective parameterization with classic HLLE.
(c) Bijective parameterization with our algorithm.
Figure 6: Parameterization results for the Left Hemisphere
- Rostral Anterior Cingulate mesh with classic HLLE and
our algorithm.
sic HLLE and our algorithm. As described in section
3.1 Classic HLLE parameterization (fig. 5(a)) com-
putes local non-bijective parameterizations at such
sharp zone. As a consequence, the parameterized sur-
face folds as detailed in fig. 5(b) resulting in a non-
bijective parameterization. On the other hand, our al-
gorithm does not face this problem and correctly un-
folds the surface recovering a bijective parameteriza-
tion (figs. 5(c) and 5(d)).
Fig. 6 presents the parameterization results for the
Right Hemisphere - Temporal Pole sub-mesh which
presents several sharp sections (fig. 6(a)) using the
classic HLLE algorithm and our algorithm. Clas-
sic HLLE fails to adequately parameterize some lo-
cal features of the surface resulting in a non-bijective
mapping (fig. 6(b)). Again, our algorithm does not
face this problem resulting in a bijective mapping (fig.
6(c)). In addition, less shape distortion can be evi-
(a) Left Hemisphere - Rostral Middle Frontal texture map.
(b) Right Hemisphere - Lateral Occipital bijective texture
map.
Figure 7: Texture map of other bijective mappings from the
Brain dataset computed with our algorithm.
denced from our algorithm compared to classic HLLE
parameterization (figs. 6(b) and 6(c)) due to the ex-
plicit computation of the local Hessian functional.
Results of our algorithm for other sub-meshes of
the Brain are presented in fig. 7. The texture map
of a chessboard pattern illustrates the angular distor-
tion of the respective parameterization where less lo-
cal distortion is present if the corners of the mapped
rectangles are near 90 degrees. All the four param-
eterizations are bijective despite the high frequencies
of the sub-meshes.
Highly non-developable meshes still pose a prob-
lem to our algorithm. Fig. 8 presents a case of the
Brain dataset where the algorithm fails to recover a
bijective parameterization. In this case the parameter-
ization degenerates near the boundary (i.e. triangles
overlap) in the parameter space due to the high non-
developability of such zones in the surface.
Finally, fig. 9 presents the texture map (computed
by our algorithm) of a chessboard pattern onto the
Face dataset. The underlying parameterization is bi-
jective, handling easily the non-convex parts (i.e. eye
holes) with low shape distortion.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
80

Table 1: Appraisal of time complexity of Mesh Parameterization algorithms. c denotes the number of iterations before
convergence for that particular algorithm while |∂M| denotes the number of vertices at the boundary of M.
Reference Algorithm Complexity
N/A Our algorithm O(c · n)
(Donoho and Grimes, 2003) Classic HLLE O(c · n)
(Floater, 1997) Floater Parameterization O(c · n)
(Yoshizawa et al., 2004) Stretch Minimizing Parameterization O(c
1
· c
2
· n)
(Desbrun et al., 2002) Intrinsic Parameterization O(c · n)
(L
´
evy et al., 2002) LSCM O(c · n)
(Lee et al., 2002) Virtual Boundary Parameterization O(c
1
· n + c
2
· |∂M|)
(Zayer et al., 2007) LinearABF O(c · n)
(Liu et al., 2008) ASAP O(c · n)
(Liu et al., 2008) ARAP O(c
1
· c
2
· n + c
3
· |∂M|)
(Sheffer and de Sturler, 2001) ABF O(c
1
· c
2
· n)
(Kharevych et al., 2006) Discrete Conformal Mappings O(c
1
· c
2
· n
(Smith and Schaefer, 2015) Free Boundary Parameterization O(c · (n + |∂M|))
(a) High Frequency - High Curvature dataset.
(b) Non-bijective parameterization of the High Frequency -
High Curvature dataset with our algorithm.
Figure 8: Failure test for our algorithm.
4.2 Time Complexity Comparison
In order to compare our algorithm with other Mesh
Parameterization algorithms, table 1 presents an ap-
praisal of the time complexity of several Mesh Pa-
rameterization algorithms. Classic HLLE and our al-
gorithm compute the first three eigenvectors of the
Hessian estimator by the Implicitly Restarted Lanczos
Figure 9: Texture map on the Face dataset computed with
our algorithm.
Method with time complexity O(c · n) (here we de-
note c ≥ 1 as the number of iterations executed by the
algorithm before convergence). Other Mesh Parame-
terization algorithms rely on solving a linear system
of equations, which is usually solved by a Conjugate
(or Bi-Conjugate) Gradient Method once (O(c · n)) or
several times (O(c
1
· c
2
· n)). It is important to note
that c is not the same between algorithms, but it is
stated that such number is relatively low in applica-
tions after matrix preconditioning as well as use of
initial parameterizations in iterative algorithms.
5 CONCLUSIONS
This article presents a variation of the classic HLLE
algorithm for parameterization of triangular meshes.
Classic HLLE was selected for this purpose since it
has shown experimentally better results than other DR
algorithms for Mesh Parameterization. An intuitive
approach from Differential Geometry is followed by
estimating locally the tangent Hessian with quadratic
Hessian Eigenfunctions for Triangular Mesh Parameterization
81

interpolation and computing a partition of unity for
the triangular mesh M as opposed to classic HLLE
approach. In addition, each local parameterization is
achieved by projecting onto the local average trian-
gle normals plane instead of the usual PCA, which
reflects better the local geometry of the surface spe-
cially in cases of sharp features.
The Brain dataset was parameterized with both
Classic HLLE and our algorithm resulting in a higher
rate of success (96.63%) for our approach against
classic HLLE (76.40%). The Face dataset was also
considered, resulting in a bijective parameterization
with low shape distortion despite having holes. Com-
plexity analysis showed that our algorithm asymptot-
ically behaves similar to Mesh Parameterization algo-
rithms that rely on solving a linear system of equa-
tions only once.
5.1 Ongoing Work
Segmentation of complex meshes with high gaus-
sian curvatures into smaller ones increases the prob-
ability of finding bijective parameterizations. There-
fore, automatic mesh segmentation for this task be-
comes crucial for parameterization of large and com-
plex datasets.
ACKNOWLEDGEMENTS
This research has been funded by the Research Group
and College of Engineering at Universidad EAFIT,
Colombia.
REFERENCES
Athanasiadis, T., Zioupos, G., and Fudos, I. (2013).
Efficient computation of constrained parameteriza-
tions on parallel platforms. Computers & Graphics,
37(6):596–607. Shape Modeling International (SMI)
Conference 2013.
Belkin, M. and Niyogi, P. (2003). Laplacian eigenmaps
for dimensionality reduction and data representation.
Neural Computation, 15(6):1373–1396.
Desbrun, M., Meyer, M., and Alliez, P. (2002). Intrinsic pa-
rameterizations of surface meshes. Computer Graph-
ics Forum, 21(3):209–218.
Desikan, R. S., S
´
egonne, F., Fischl, B., Quinn, B. T., B,
C. D., Blacker, D., Buckner, R. L., Dale, A. M.,
Maguire, R. P., Hyman, B. T., Albert, M. S., and Kil-
liany, R. J. (2006). An automated labeling system
for subdividing the human cerebral cortex on +mri
scans into gyral based regions of interest. NeuroIm-
age, 31(3):968–980.
Donoho, D. L. and Grimes, C. (2003). Hessian eigen-
maps: Locally linear embedding techniques for high-
dimensional data. Proceedings of the National
Academy of Sciences, 100(10):5591–5596.
Floater, M. S. (1997). Parametrization and smooth approxi-
mation of surface triangulations. Computer Aided Ge-
ometric Design, 14(3):231–250.
Kharevych, L., Springborn, B., and Schr
¨
oder, P. (2006).
Discrete conformal mappings via circle patterns. ACM
Transactions on Graphics, 25(2):412–438.
Lafon, S. and Lee, A. (2006). Diffusion maps and coarse-
graining: a unified framework for dimensionality re-
duction, graph partitioning, and data set parameteriza-
tion. Pattern Analysis and Machine Intelligence, IEEE
Transactions on, 28(9):1393–1403.
Lee, Y., Kim, H. S., and Lee, S. (2002). Mesh parameteriza-
tion with a virtual boundary. Computers & Graphics,
26(5):677–686.
L
´
evy, B., Petitjean, S., Ray, N., and Maillot, J. (2002). Least
squares conformal maps for automatic texture atlas
generation. In ACM, editor, ACM SIGGRAPH con-
ference proceedings.
Liu, L., Zhang, L., Xu, Y., Gotsman, C., and Gortler, S. J.
(2008). A local/global approach to mesh parameteri-
zation. In Proceedings of the Symposium on Geometry
Processing, SGP ’08, pages 1495–1504, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
Roweis, S. T. and Saul, L. K. (2000). Nonlinear dimension-
ality reduction by locally linear embedding. Science,
290(5500):2323–2326.
Ruiz, O. E., Mejia, D., and Cadavid, C. A. (2015). Trian-
gular mesh parameterization with trimmed surfaces.
International Journal on Interactive Design and Man-
ufacturing (IJIDeM), pages 1–14.
Sheffer, A. and de Sturler, E. (2001). Parameterization of
faceted surfaces for meshing using angle-based flat-
tening. Engineering with Computers, 17(3):326–337.
Smith, J. and Schaefer, S. (2015). Bijective parameteri-
zation with free boundaries. ACM Transactions on
Graphics, 34(4):70:1–70:9.
Sun, X. and Hancock, E. R. (2008). Quasi-isometric param-
eterization for texture mapping. Pattern Recognition,
41(5):1732–1743.
Tenenbaum, J. B., de Silva, V., and Langford, J. C. (2000).
A global geometric framework for nonlinear dimen-
sionality reduction. Science, 290(5500):2319–2323.
Yoshizawa, S., Belyaev, A., and Seidel, H.-P. (2004). A
fast and simple stretch-minimizing mesh parameteri-
zation. In Shape Modeling Applications, 2004. Pro-
ceedings, pages 200–208.
Zayer, R., L
´
evy, B., and Seidel, H.-P. (2007). Linear angle
based parameterization. In ACM/EG Symposium on
Geometry Processing conference proceedings.
Zhang, Z. and Zha, H. (2002). Principal manifolds and
nonlinear dimension reduction via local tangent space
alignment. SIAM Journal of Scientific Computing,
26:313–338.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
82
