Generating Temporal Network Paths from Hospital Data

John Michael Finney and Laura Madrid Marquez

National Institute for Health Research Oxford Biomedical Research Centre, University of Oxford, Oxford, U.K.

Oxford University Hospitals NHS Trust, John Radcliffe Hospital, Oxford, U.K.

Nuffield Department of Medicine, University of Oxford, Oxford, U.K.

Keywords: Graph Database, Temporal Networks, Neo4j, Cypher, Electronic Medical Records.

Abstract: Using data from electronic medical records we were able to rapidly generate temporal network data. This

data can then be loaded into a modern graph database and used to generate a temporal graph of the data.

Using a specialist graph language for rapidly querying these graph databases, we are able to rapidly extract

temporal path information about patient to patient contact networks based on shared ward encounters. This

information can then be used to calculate various network statistics of interest that may be important for

clinical use.

1 INTRODUCTION

Construction of social networks of hospital patients

based on shared ward contacts or other potential

disease transmission vectors has the potential to

allow interesting analysis to be done which may

provide useful actionable results to infection control

professionals (Cusumano-Towner et al., 2013;

Walker et al., 2012).

Electronic medical records provide a rich source

of data which can be readily used to generate these

social networks for the study of infectious disease

transmission within hospitals (Cusumano-Towner et

al., 2013). As we have complete knowledge of

patient ward based movements, we are able to use

electronic records to construct the complete network

structure allowing us to measure directly various

properties of the network without having to resort to

various network approximation methods to guess at

missing data (Danon et al., 2011).

Traditional network statistics fail to capture the

dynamic process inherent in disease transmission

(Holme and Saramäki, 2012). More recently there

has been extensive work on temporal network

models which allow us to capture the dynamic

nature of networks and achieve more relevant results

(Holme and Saramäki, 2012; Valdano et al., 2015).

We need to make sure our models and methods are

appropriate for handling temporal network data.

Many important concepts within disease

transmission can be modelled using network

analysis (Holme and Saramäki, 2012). Concepts

such as contact tracing, network centrality and

reachability among others may provide important

information to clinical staff which can then be used

to make important decisions regarding patient care

(Masuda and Holme, 2013; Cooper et al., 1999).

Due to the large datasets and relatively dense

network structure of patient connections we are

interested in using new tools to allow us to calculate

these various measures easily using newer temporal

data models.

Here we present an implementation of a

temporal network model of shared ward contacts and

show examples of how this can be used to rapidly

calculate temporal network paths which can be used

to calculate network statistics, very rapidly on large

datasets using modern software tools, which may be

important for infection control purposes.

2 MATERIALS AND METHODS

2.1 Ethics

Data for this work was obtained from the Infections

in Oxfordshire Research Database (IORD) (Finney

et al., 2011), a linked data warehouse of anonymised

patient records. IORD has Research Ethics

Committee and Health Research Authority approval

as a generic infectious disease electronic research

database (14/SC/1069, ECC5-07(A)/2009).

Finney, J. and Marquez, L.

Generating Temporal Network Paths from Hospital Data.

DOI: 10.5220/0005669402630268

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 5: HEALTHINF, pages 263-268

ISBN: 978-989-758-170-0

263

The work described here represents the network

engine used in the IORD approved study,

“asymptomatic carriage candidate selection”.

2.2 Network Model

In order to model our data, we have used the same

methods as described in (Holme and Saramäki,

2012). We have timestamped (YYYY-MM-DD

hh:mm) all our relationships and our code takes

account of this when traversing the network.

Traditional network models often aggregate links

between nodes over a period of time and calculate

statistics based on this (Holme and Saramäki, 2012);

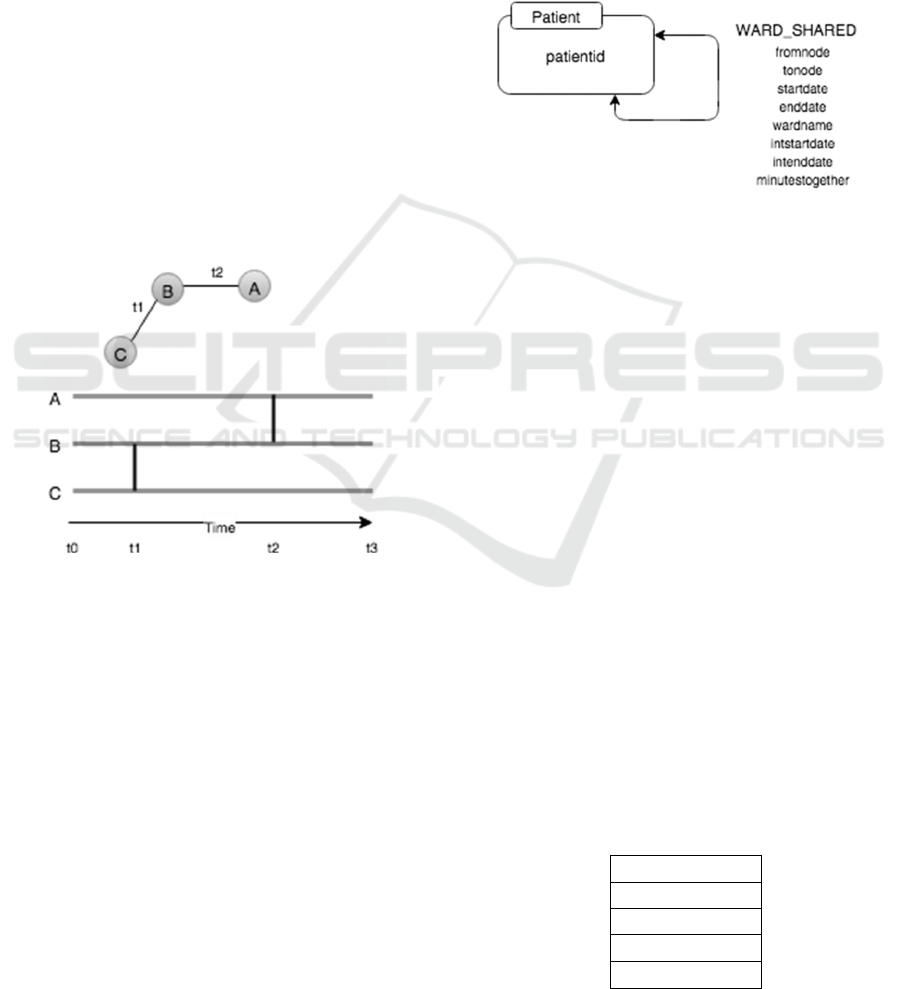
(Valdano et al., 2015). As can be seen from the

Figure 1 below, this aggregation over a period of

time does not reflect the true nature of the network.

As an example node A cannot ever reach node C as

following the temporal links between nodes never

allow this. The link between nodes A and B occurs

after the link between B and C never allowing the

connection of A and C.

Figure 1: We can easily see that if we start from node A,

we can never reach node C as the connection between the

intermediate link, B, and the final destination C happens

before the link from A to B.

In a more traditional static aggregated analysis

all the relationships within a time period would be

aggregated. In this example if we aggregate all

relationships from t0 to t1 we would then have a

path connecting all nodes at any point during this

time. In this very simple example the difference in

conclusions can be clearly seen.

For the purposes of our work we have

implemented our network using the property graph

(Sun et al., 2015) in Figure 2. The graph represents

the hospital patient to patient contact network, a

subset of a larger network model we are working on.

Each node in the graph represents a single

patient. The properties of the node represent various

demographics about the patient, which we are not

using in this example. All of this data can be used

later for studying the graph using any properties of

interest. Initially we are just concerned with our

patient and their contact with other patients based on

a shared ward space.

The edge connection from one patient to another

is a timestamped relationship representing the time

(YYYY-MM-DD hh:mm) and location the patients

came into contact in the hospital. This data is readily

extracted from IORD.

Figure 2: Here we have a simple property graph model

representing patient connections. Each Patient node

represents one unique patient in our data set. Patients are

linked with timestamped (YYYY-MM-DD hh:mm) edges

representing the date and time of contact, the place of

contact and the length of time, in minutes, the contact

occurred. This simple model provides enough information

for a range of temporal graph queries.

2.3 IORD Patient Data

In order to populate our models, we needed to

extract two sets of data. This data was generated

from IORD. The first set of data was a set of all

unique identifiers representing all inpatients in the

hospital between April 2008 and April 2011. The

fields for this data are listed in Table 1. This

represented 244331 unique individuals.

The second set of data described in Table 2,

represented the timestamped edges of the graph. The

represented patient to patient contacts based on

sharing the same ward at the same time. They

contained information over the same period and

represented 21284670 patient to patient contacts.

Table 1: nodeid is a unique identifier representing the

individual node. patientid is the unique id representing a

single patient with the birthdate and gender as given in the

fields, dob and gender.

Node Table

nodeid

patientid

dob

gender

HEALTHINF 2016 - 9th International Conference on Health Informatics

264

Table 2: Edgeid represents a unique value representing a

single overlapping time when two patients were in the

same ward at the same time. Startdate represents the time

the contact began with the endtime representing the end.

Wardname is the ward that they shared. Intstartdate and

intenddate are integer representations of the above dates to

make future graph traversal easier to handle. Minutes

together represents the length of time shared in the same

ward space in minutes and will be used in further analysis.

Edge Table

edgeid

fromnode

tonode

wardname

startdate

enddate

intstartdate

intenddate

minutestogether

Data was extracted from IORD, which is

contained in an MSSQL2014 database, and extracted

using TSQL.

2.4 Graph Database

Much of the electronic data within a hospital setting

is traditionally held in a relational database (Wyllie

and Davies, 2015). Although these databases work

extremely well and efficiently for relational models,

they perform poorly when trying to analyse data in a

network model structure (Rodriguez and Neubauer,

2010).

New types of NoSQL databases have emerged

over recent years to handle other types of non-

relational data (Ciglan et al., 2012). For our work we

use a specialist graph database, NEO4j, which

natively models data in a graph format and allows

for very rapid traversals. NEO4j allows one to easily

extract data from your normal relational database

and import it easily into a graph model.

2.5 Cypher Query Language

Once we have loaded our data into our NEO4j

model, we are able to then do temporal graph

traversals. The results of these traversals can then be

used either directly to calculate various properties of

the graph in question or the output can then be fed

into traditional tools to generate statistics of interest.

NEO4j uses a powerful declarative graph query

language called Cypher (Webber, 2012). This

language allows for extremely fast and expressive

queries across graph data models.

We implemented the following pseudo code in

neo4j:

Traverse paths between two nodes

Store results in "PATHS"

FOR EACH "PATH" in "PATHS"{

FOR EACH relationship in "PATH"{

IF relationship timestamp >

previous relationship timestamp

AND is within the range of

interest{

Keep this path and continue

checking.

}ELSE{

Discard this path.

}

Path complete. Keep this path.

}

Return all successful paths.

This pseudocode was implemented in neo4j

using the following to traverse the graph across a

temporal network.

MATCH path = allshortestpaths((

p:Patient{patientid:"11111"})

-[w:WARD_SHARE*..]->

(q:Patient{patientid:"22222"}))

with path,

EXTRACT(r in relationships(path) |

r.ward) as final with path,

final,

REDUCE(acc = [0,1], r in

relationships(path) |

CASE WHEN

r.intstartdate>acc[0] and

r.startdate>{some_date} and

r.startdate<{some_date}

THEN

[r.intstartdate, acc[1]*1]

ELSE

[r.intstartdate, acc[1]*0]

END

)[1] as test

where test=1

return path;

This cypher query calculates the paths between

two given nodes, 11111 and 22222. It tests each new

branch within an individual path to make sure that

the path represents a step forward in time. The end

result is a list of shortest paths between two nodes

based on the number of hops between nodes. All of

these paths all represent movements forward in time.

Using a java (Gosling, 2000) interface we were

able to connect the graph database to our relational

dataset to run multiple queries over many patients’

connections to calculate various temporal graph

paths of interest.

Generating Temporal Network Paths from Hospital Data

265

3 RESULTS

For the purposes of testing our graph database we

loaded 3 years of hospital admission, discharge and

transfer (ADT) data from IORD into NEO4j. We

used NEO4j enterprise version 2.21. This was run on

a Windows 2008 R2 server with 32GB ram and 16

cores.

The data from April 2008 to April 2011

consisted of 122 wards, 244331 unique patients and

21284670 shared ward contacts between these

patients.

This data was loaded into neo4j using the native

cypher loader. The 244331 nodes in the data set

loaded in 10.4 second using the following cypher

query:

Using periodic commit 500

Load csv with headers from

“file:f:neo4jnodes.csv” as row

Create (p:Patient)

Set p=row;

Create index on :Patient(patientid);

The 21284670 relationships in the data set was

loaded using the following query in 93 minutes.

Using periodic commit 500

Load csv with headers from

“file:f:neorjrelations.csv” as line

Match

(pa:Patient{patientid:line.patient1}

(pb:Patient{patientid:line.patient2}

)

Create (pa)-[:WARD_SHARE

{ward:line.ward,

startdate:line.joindate,

intstartdate:toInt(line.joinminute),

enddate:line.enddate,

intenddate:toInt(line.endminute),

minutestogether:toInt

(line.minutestogether),

fromnode:line.patienti1,

tonode:line.patient2}]

->(pb);

In order to test the speed of path generation for

different paths, we first retrieved all anonymous

identifiers for patients that had completed a C.diff

test during the period of our data set.

From this we initially chose March 1 2009 as our

initial index day. Paths were generated between all

patients on the index day that had a C.diff test as

well as all patients that had been tested for C.diff at

1,2,3,4,5,6,7,14,28,90,180 and 360 days. This was

repeated for the following days until March 31 2009.

The results of the timings can be found in Figure 3.

This resulted in the search of 363823 potential

shortest paths between pairs of patients on different

days over a temporal network. The average time for

each path was 0.0717 (SD=0.0283) seconds.

Figure 3: This shows the timings for traversing all the

paths in the set of interest. The squares show the total

traversals for a given index day and the diamond shows

the successful traversals where a path was actually found.

4 DISCUSSION

So far we have shown that we are able to load large

patient to patient contact networks into a temporal

data model using NEO4j and then apply cypher

queries to efficiently extract paths between patients

very quickly.

On an individual basis, this information

potentially allows you to know all contacts rapidly

going backwards or forwards in time from a key

patient. Depending on the situation, it may provide a

rapid method of generating timely information for

relevant clinicians.

Once we start aggregating results from multiple

paths we can potentially start to find interesting

results. For example it is now trivial with a temporal

model to calculate a reachability ratio (Holme, 2005)

(Holme and Saramäki, 2012) of infection from one

ward (assuming person to person in ward contact is

the vector of transmission). This might provide

important information for deciding for example

which ward to place patients in order to minimise

the risk of infection reaching them from other wards.

It may also provide extra information to help decide

to close a ward or provide extra cleaning if the ward

has a high probability of spreading infection to other

parts of the hospital.

Other temporal network statistics can also

readily be calculated from aggregated path data

(Holme and Saramäki, 2012). Some examples are

centrality measures, diameter, latency and contact

networks.

HEALTHINF 2016 - 9th International Conference on Health Informatics

266

A number of studies of infectious disease have

reported on the importance of various centrality

measures to determine the most important nodes in

the network with regards to the disease in question

(Christley et al., 2005). With a temporal graph

model in place we can now readily calculate various

centrality measures of interest and then act

accordingly (Holme and Saramäki, 2012).

Recent studies have shown the importance of

using temporal network models for the SIR and

similar compartmental models (Holme and Masuda,

2015).

Traditional SIR models across networks link

pairs of individuals if there is a direct link during a

sampling period. When looking at the same data

through a temporal network it becomes obvious that

many paths in the model do not actually exist. The

end result can be completely different to the

traditional static aggregated model and can

potentially result in errors such as having a

reproductive number greater than 1 when in fact the

disease is actually dying out (Holme and Masuda,

2015).

Here with the framework we present we are able

to extract the required temporal data rapidly and

calculate various statistics as required.

5 CONCLUSIONS

Temporal graphs provide an important source of

statistical data. Several studies have suggested that

this data may provide information that may be

important for clinical use such as providing clues

about infection transmission (Holme and Saramäki,

2012); (Walker et al., 2012). However the extraction

of this data from hospital records has traditionally

been complicated and has required specialist tools

and knowledge to extract.

We have developed a simple way of using a

standard off the shelf graph database, connecting

this database to our local relational Infection

research database (IORD) and converting our data to

a temporal graph model which can then be used for

calculating various temporal graph statistics of

interest.

This work is important as it offers a way to

implement an important network algorithm which

can be used for infection control purposes that

would otherwise be hard to do and require specialist

tools and extensive custom programming.

We are currently using this model as the backend

for two research projects investigating various

aspects of infectious disease transmission within a

hospital setting.

In the future we hope to integrate further

algorithms into our work and potentially integrate

this into a live system.

ACKNOWLEDGEMENTS

The research was supported by the National Institute

for Health Research (NIHR) Oxford Biomedical

Research Centre based at Oxford University

Hospitals NHS Trust and University of Oxford.

REFERENCES

Cusumano-Towner, M., Li, D., Tuo, S., Krishnan, G. and

Maslove, D. (2013). A social network of hospital

acquired infection built from electronic medical

record data. Journal of the American Medical

Informatics Association, 20(3), pp.427-434.

Walker, A., Eyre, D., Wyllie, D., Dingle, K., Harding, R.,

O'Connor, L., Griffiths, D., Vaughan, A., Finney, J.,

Wilcox, M., Crook, D. and Peto, T. (2012).

Characterisation of Clostridium difficile Hospital

Ward Based Transmission Using Extensive

Epidemiological Data and Molecular Typing. PLoS

Med, 9(2), p.e1001172.

Danon, L., Ford, A., House, T., Jewell, C., Keeling, M.,

Roberts, G., Ross, J. and Vernon, M. (2011). Networks

and the Epidemiology of Infectious Disease.

Interdisciplinary Perspectives on Infectious Diseases,

2011, pp.1-28.

Barnes, S., Golden, B. and Wasil, E. (2010). A dynamic

patient network model of hospital-acquired infections.

Proceedings of the 2010 Winter Simulation

Conference.

Holme, P. and Saramäki, J. (2012). Temporal networks.

Physics Reports, 519(3), pp.97-125.

Valdano, E., Ferreri, L., Poletto, C., & Colizza, V. (2015).

Analytical computation of the epidemic threshold on

temporal networks. Physical Review X, 5(2), 021005.

Masuda, N. and Holme, P. (2013). Predicting and

controlling infectious disease epidemics using

temporal networks. F1000Prime Rep, 5.

Christley, R. (2005). Infection in Social Networks: Using

Network Analysis to Identify High-Risk Individuals.

American Journal of Epidemiology, 162(10), pp.1024-

1031.

Cooper, B., Medley, G. and Scott, G. (1999). Preliminary

analysis of the transmission dynamics of nosocomial

infections: stochastic and management effects. Journal

of Hospital Infection, 43(2), pp.131-147.

Sun, W., Fokoue, A., Srinivas, K., Kementsietsidis, A.,

Hu, G., & Xie, G. (2015, May). SQLGraph: An

Efficient Relational-Based Property Graph Store.

Generating Temporal Network Paths from Hospital Data

267

In Proceedings of the 2015 ACM SIGMOD

International Conference on Management of Data (pp.

1887-1901). ACM.

Finney, J., Walker, A., Peto, T. and Wyllie, D. (2011). An

efficient record linkage scheme using graphical

analysis for identifier error detection. BMC Med

Inform Decis Mak, 11(1), p.7.

Taxiarchis Botsis, C. (2010). Secondary Use of EHR:

Data Quality Issues and Informatics Opportunities.

Summit on Translational Bioinformatics, [online]

2010, p.1. Available at:

http://www.ncbi.nlm.nih.gov/pmc/articles/PMC30415

34/ [Accessed 9 Sep. 2015].

Ciglan, M., Averbuch, A. and Hluchy, L. (2012).

Benchmarking Traversal Operations over Graph

Databases. 2012 IEEE 28th International Conference

on Data Engineering Workshops.

Rodriguez, M. and Neubauer, P. (2010). The Graph

Traversal Pattern. [online] Arxiv.org. Available at:

http://arxiv.org/abs/1004.1001 [Accessed 9 Sep.

2015].

Jim Webber. 2012. A programmatic introduction to Neo4j.

In Proceedings of the 3rd annual conference on

Systems, programming, and applications: software for

humanity (SPLASH '12). ACM, New York, NY, USA,

217-218.

Gosling, J. (2000). The Java language specification.

Addison-Wesley Professional.

Holme, P. (2005). Network reachability of real-world

contact sequences.Physical Review E, 71(4), 046119.

Borgatti, S. P. (2005). Centrality and network flow. Social

networks, 27(1), 55-71.

Bell, D. C., Atkinson, J. S., & Carlson, J. W. (1999).

Centrality measures for disease transmission

networks. Social networks, 21(1), 1-21.

Christley, R. M., Pinchbeck, G. L., Bowers, R. G., Clancy,

D., French, N. P., Bennett, R., & Turner, J. (2005).

Infection in social networks: using network analysis to

identify high-risk individuals. American journal of

epidemiology, 162(10), 1024-1031.

Rocha, L. E., Liljeros, F., & Holme, P. (2011). Simulated

epidemics in an empirical spatiotemporal network of

50,185 sexual contacts. PLoS Comput Biol, 7(3),

e1001109.

Wyllie, D., & Davies, J. (2015). Role of data warehousing

in healthcare epidemiology. Journal of Hospital

Infection, 89(4), 267-270.

Easley, D., & Kleinberg, J. (2010). Networks, crowds, and

markets: Reasoning about a highly connected world.

Cambridge University Press.

Holme, P., & Masuda, N. (2015). The basic reproduction

number as a predictor for epidemic outbreaks in

temporal networks. PloS one, 10(3), e0120567.

HEALTHINF 2016 - 9th International Conference on Health Informatics

268