
Sensor Localization using Signal Receiving Probability
and Procrustes Analysis
Ashanie Gunathillake
1,2
, Andrey V. Savkin
1
, Anura Jayasumana
3
and Aruna Seneviratne
1,2
1
School of Electrical Engineering and Telecommunication, University of New South Wales, Sydney NSW 2052, Australia
2
NICTA, Eveleigh, NSW 2015, Australia
3
Department of Electrical and Computer Engineering, Colorado State University, Fort Collins, CO 80523, U.S.A.
Keywords:
Localization, Procrustes Analysis, Signal Propagation, Wireless Sensor Network.
Abstract:
The location information of sensors is of great importance for wireless sensor network automation and has
been one of the major challenges in large-scale sensor networks. In order to improve the localization accuracy
of sensors, the gain of both range-free and range-based approaches need to be concerned. In this paper,
we propose a new localization algorithm based on signal receiving probability and Procrustes analysis. A
critical observation in range-free technique is sensors can move a non-zero distance without changing it’s
connectivity information. To defeat that difficulty and achieve a better ranging measurement, a receiving
probability function, which is sensitive to the distance, is used in this paper. The probability function is used
to calculate the topological coordinates and then to transform it to physical coordinates, the Procrustes analysis
is used. The result shows that our proposed algorithm has been able to calculate the physical coordinates of
sensors, which are distributed over an area, consist of obstacles and with different environmental conditions.
Moreover, it outperformed the other existing algorithms by a maximum localization error less then 2m.
1 INTRODUCTION
Wireless Sensor Networks (WSNs) applications cover
a large number of domains spanning environmen-
tal monitoring, military, agriculture, transportation
and inventory tracking (Garca-Hernndez et al., 2007)
(Tubaishat and Madria, 2003). Future WSNs will be
large-scale networks automated to self-organized and
perform a specific task. Thus, the location map of the
sensors is required.
However, finding the locations of the sensors is
crucial and has received substantive attention in re-
cent years. The algorithms used to calculate the
physical coordinates of the sensors can be divided
into two categories, namely Range-based and Range-
free localization algorithms. Range-based algorithms
use special hardware component to measure range-
based parameters such as received signal strength
(RSS) (Chengdong et al., 2011), time of arrival(TOA)
(Wang and Ho, 2013), angle of arrival (AOA) (Kotwal
et al., 2010). These algorithms are affected by noise,
fading and interference, and as a result, their accuracy
decreases in environments with obstacles. Range-free
algorithms rely on the information about the connec-
tivity of the sensors instead of using special hardware
device. However, the accuracy of the algorithms is
highly depended on the number of anchor nodes i.e.
nodes known their locations, and their distribution.
To this end, we are proposing a localization algo-
rithm based on Receiving Probability and Procrustes
Analysis (RP-PA). Here we are trying to achieve the
advantages in both range-based and range-free tech-
niques. As in range-free algorithms we do not use
any special hardware component, but to calculate the
distances, a signal receiving probability function that
is sensitive to the distance is used. Since we are not
using any hardware component to measure the dis-
tances, the hardware cost of the network can mini-
mize.
RP-PA algorithm uses a receiving signal probabil-
ity function to reduce the dependency on range-based
measurements. It starts from finding the topology
map of the network using the probability function.
Topology map is an arrangement of nodes without af-
fecting it’s connectivity information. In RSSI based
algorithms, the distances are extracted from receiv-
ing power that encounters some error due to RF com-
munication effects. Thus, we evaluate the connectiv-
ity information without taking those error prone pa-
rameters. In range-free algorithms, they consider the
Gunathillake, A., Savkin, A., Jayasumana, A. and Seneviratne, A.
Sensor Localization using Signal Receiving Probability and Procrustes Analysis.
DOI: 10.5220/0005671301130120
In Proceedings of the 5th International Confererence on Sensor Networks (SENSORNETS 2016), pages 113-120
ISBN: 978-989-758-169-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
113

connectivity information with the hop counts to the
anchor nodes, but it is not sensitive to the distance.
As a result, it is possible to move a sensor node over
a non-zero distance without changing the hop count.
Hence, range-free algorithms generate physical coor-
dinates with less accuracy. To overcome this problem,
we construct the connectivity information matrix us-
ing a probability function, which is sensitive to the
distance between sensor nodes.
To transform the topology coordinates to physical
coordinates, the algorithm uses the Procrustes Analy-
sis. From the result, it can be seen that the proposed
RP-PA algorithm is able to provide accurate physical
coordinates of the sensors. Also, it results in an error
less than 2m and outperforms the RSSI and hop-based
localization algorithms.
2 BACKGROUND
Prior work on localization techniques, can be grouped
into two categories range-based and range-free local-
ization. In range-based techniques special hardware
device is used to measure the range-based parameters
such as signal strength, time of arrival and angle of
arrival. In received signal strength indicator (RSSI)
based localization algorithms, signal strength of re-
ceiving packets is used to estimate the distance be-
tween nodes. The distance calculation of these algo-
rithms use two models namely, theoretical and em-
pirical models (Zhang et al., 2012). In theoretical
models, RF signal transmission loss model is used
to directly calculate the distance between two nodes
(Mukhopadhyay et al., 2014)(Al Alawi, 2011). The
empirical models, use a two steps process to ob-
tain the location. First, they create an offline RSSI
database, using anchor nodes. Secondly, it determines
the coordinates of non-anchor nodes by matching the
received signal strength to a record of the database
(Chengdong et al., 2011)(Wanga et al., 2011).
The localization method based on time difference
of arrival (TDOA) estimates the coordinates of an un-
known node by anchor nodes’ coordinates and time
difference of arrival from those anchors to the node.
For the calculation, it needs at least four anchors
(Savarese et al., 2002) (Luo et al., 2012) (Liu et al.,
2012) (Wang and Ho, 2013) (Huang et al., 2015).
Furthermore, in time of arrival (TOA) based local-
ization, the anchor nodes broadcast a signal and the
sensor nodes that receive these broadcasts, use the
time difference of arrival , RSS and a the angle of
arrival to determine their locations. This requires
the sensor timers have to be synchronized. To over-
come this requirement, researchers have proposed the
use of Round-Trip TOA (RTOA) (Wymeersch et al.,
2009) and Two Way TOA (TW-TOA) (Gholami et al.,
2012)(Oguz-Ekimet al., 2013). Again, TOA localiza-
tion does not address issues associated with obstacles
and RF signal transmission affects.
In range-free localization algorithms, the loca-
tions of nodes are obtained without using any spe-
cial hardware. They rely on the connectivity infor-
mation of nodes. First, it gets the distance in hops
and then maps the hop distance to geometric distance
(Niculescu and Nath, 2003)(Tian et al., 2003)(Liu
et al., 2004) using anchor node locations. Therefore,
the accuracy of these algorithms highly depends on
the number of anchor nodes and their deployment.
The key issue of range-free algorithms is the distance
estimation i.e. the mapping of the hop distance to ge-
ometric distance.
Dulanjalie et al. (Dhanapala and Jayasumana,
2014) presented a method to obtain topology-
preserving maps of WSNs using virtual coordinates
(VCs) of sensor nodes. Topological mapping tech-
niques are fundamentally different to localization
techniques because the mapping algorithms are con-
cerned with the arrangement of the nodes. They are
not concerned about the actual location of the nodes.
In other words, the mapping schemes expect the rel-
ative distances to be accurate, not the physical dis-
tances. Thus, given the absolute position of a subset
of nodes, global localization is realizable. However,
to achieve this, the topological map should be isomor-
phic to the physical layout of the sensor network. In
Virtual Coordinate System (VCS), the layout infor-
mation such as physical voids, shape, and etc. are
absent. Furthermore, Dulanjalie et al.(Dhanapala and
Jayasumana, 2014) have shown that transformation
for topological map from virtual coordinates can be
generated using a subset of nodes. However, when the
number of nodes increase, the time required to gener-
ate the virtual coordinate matrix also increases.
3 DETAILS OF THE PROPOSED
ALGORITHM: RP-PA
This section describes the work flow of RP-PA algo-
rithm, that calculates the physical coordinates of the
sensors. The physical map is achieved by using the
packet receiving probability function and Procrustes
transformation. RP-PA algorithm consider two as-
pects i.e. accuracy of range measurements and the
accuracy of the coordinate. The range measurement
accuracy is obtained by the receiving signal proba-
bility function sensitive for the distance. First using
the probability values, the topological coordinates of
SENSORNETS 2016 - 5th International Conference on Sensor Networks
114

each node is calculated. Then to achieve the local-
ization accuracy, Procrustes analysis is carried out in
each node. The detail of the algorithm is described in
following subsection.
3.1 Topological Coordinates
The first task of the RP-PA algorithm is to calculate
the coordinate of nodes in topological map. Topol-
ogy map represents the arrangement of nodes without
affecting the connectivity information of nodes. To
find the connectivity information, receiving probabil-
ity function, which describes below, is used.
3.1.1 The Receiving Probability Function
This function describes the probability of packet re-
ceiving from sensor when anchor node is located at a
particular distance. Let, S(d) be the probability value
when anchor node is at distance d from the sensor.
Then, S(d) satisfies the following constraints:
0 ≤ S(d) ≤ 1 ∀d
S(d
1
) ≤ S(d
2
) ∀d
1
≥ d
2
S(d) = 0 ∀d > R (1)
where R > 0 is some given distance.
Such a function S(d) is called the receiving prob-
ability function. We will use the following example
of such a function:
S(d) := p
0
∀d ≤ r
S(d) := 0 ∀d ≥ R
S(d) :=
p
0
(R− d)
(R− r)
∀r < d < R (2)
where 0 < p0 ≤ 1, 0 < r < R < R
c
are some given
constants. R
c
is the communication range of a sensor
node. It is obvious that the function (2) satisfies all
the conditions (1).
The receiving probability function we are using
is an intermediate model of RSSI signal receiving
and hop-based packet receiving. As shown in Fig-
ure 1, it can be seen that hop based algorithms use the
r = R assumption, which cannot be achieved in real
environment. On the other hand, RSSI localization
uses a polynomial function to estimate packet receiv-
ing probability, which is hard to estimate the parame-
ters for different environmental situations. Therefore,
here we consider an intermediate level between RSSI
model and VC model to obtained the topological co-
ordinates.
Distance
Packet receiving probability
Linear decay model
RSSI model
VC model
p
0
R
r
Figure 1: Packet receiving probability function for different
models.
3.1.2 Calculating Topological Coordinates
This section describes the topological coordinate cal-
culation using the receiving probability function. Let
consider a network consist with N number of steady
sensors in unknown locations labeled i = 1, 2,..., N
and M(< N) number of steady anchor nodes that
know their locations labeled A
j
, j = 1, 2...M. The an-
chor nodes transmit signals at times t
1
< t
2
< ... < t
S
to it’s one-hop neighborhood. We introduce a binary
matrix M
i
of order a× S by the following rule. Here,
a is the number of anchor nodes in node i’s neighbor-
hood.
M
i
( j, s) = 1, if node i gets a signal from the anchor A
j
at the time t
s
;
M
i
( j, s) = 0, if node i does not get a signal from the
anchor A
j
at the time t
s
.
Then, based on the M
i
matrix, signal receiving
probability matrix RP
i
of order a× 1is deduced as fol-
lows.
RP
i
( j, 1) =
∑
S
s=1
M
i
( j, s)
S
(3)
Finally, based on the anchor node positions,
the receiving probability function S(d) and the
receiving probability matrix RP
i
, we obtain the
topological coordinates of the sensors. Let
AP
i
(1, 1), AP
i
(2, 1), ..., AP
i
(a, 1) denote the elements
of the vector AP
i
. Furthermore, the probability for
a sensor node to receive a signal from a anchor
node A
j
is described by the function S(d) where d
is the distance between the anchor and the sensor
node i at the time of sending the signal. Thus we
can map the probability values to a distance vector
using the receiving probability function denoted as
d
i
(1, 1), d
i
(2, 1)...d
i
(a, 1) respectively.
After knowing the distance of the vector of sen-
sor i, we have used trilateration to calculate the co-
ordinate of the node with respect to the anchors
in its first hop neighborhood. The coordinates of
the anchors in node i’s first hop neighborhood are
Sensor Localization using Signal Receiving Probability and Procrustes Analysis
115
0 5 10 15 20 25 30
0
5
10
15
20
25
30
(a)
0
10
20
30
0
10
20
30
0
5
10
X
Y
Localization Error
1
2
3
4
5
6
7
8
(b)
0 5 10 15 20 25 30
0
5
10
15
20
25
30
(c)
0
10
20
30
0
10
20
30
0
5
10
X
Y
Localization Error
1
2
3
4
5
6
7
(d)
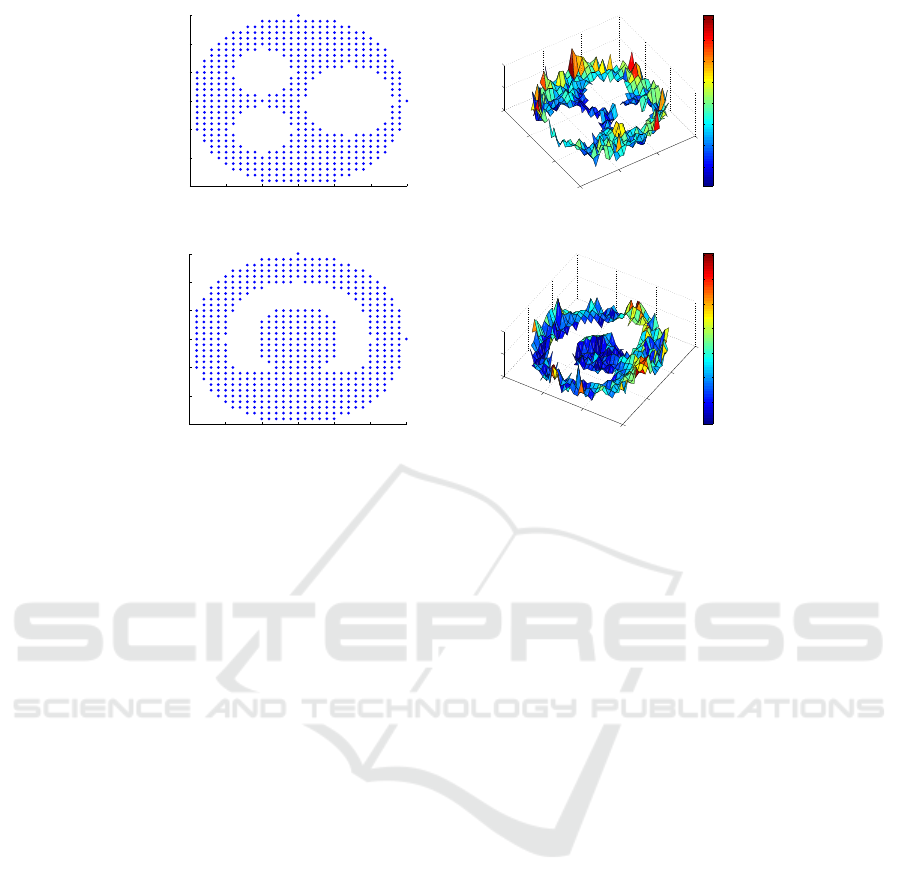
Figure 2: (a) Circular-shaped network, (b) Error distribution, (c) Concave void network and (d) Error distribution.
(x
1
, y
1
), (x
2
, y
2
)...(x
a
, y
a
). The topological coordinate
of the node i is (x
t
i
, y
t
i
) is given by the equation 4.
AX
t
= B (4)
where,
A =
2x
t
i
(x
a
− x
1
) 2y
t
i
(y
a
− y
1
)
2x
t
i
(x
a
− x
2
) 2y
t
i
(y
a
− y
2
)
.
.
.
.
.
.
2x
t
i
(x
a
− x
a−1
) 2y
t
i
(y
a
− y
a−1
)
,
X
t
=
x
t
i
y
t
i
and
B =
(x
2
a
− x
2
1
) + (y
2
a
− y
2
1
) + (d
i
(a, 1) − d
i
(1, 1))
.
.
.
(x
2
a
− x
(
a− 1)
2
) + (y
2
a
− y
(
a− 1)
2
)+
(d
i
(a, 1) − d
i
(1, 1))
,
To find an optimal topological coordinates of the
sensors, we used the Least square approximation.
Here the objective function is given as in condition 6
and by solving to X
∗t
we got the solution as in equa-
tion .
Min k AX
∗t
B k
2
(5)
X
∗
= (AA)
−1
(A)B (6)
where, X
∗
= [x
∗t
i
y
∗t
i
]
T
3.2 Obtaining Physical Coordinates
using Procrustes Analysis
This section describes the transformation of topolog-
ical coordinates to physical coordinates using Pro-
crustes analysis. Procrustes Analysis is used to align
two sets of data points. Here we used it to obtain
physical coordinate of sensors from the topological
coordinates that is calculated in the previous section.
Procrustes analysis calculates the scaling factor,
rotation angle and shift between the two sets (Nhat
et al., 2008). If the transformation between the two
sets is not linear, Procrustes analysis will find the
transformation which has an error. Thus we need
to make sure that topological coordinates have lin-
earized error with the actual sensor location. Figure
2 shows the error distribution of the topological co-
ordinates with respect to the actual positions of the
sensor nodes. According to the figure, the error dis-
tribution is not linear for the whole network. Hence, a
single transformation can not be applied to the whole
network.
To overcome that problem, transformation factors
are calculated in each node based on it’s one hop an-
chor nodes. Let consider sensor node i have a number
of anchor nodes in it’s first hop neighborhood. Then
X and Y are the topological and physical coordinate
matrices with length of a × 2 respectively. Thus the
transformation factors of node i can be estimated by
equation 7.
SENSORNETS 2016 - 5th International Conference on Sensor Networks
116

Y = bXT + c; (7)
where b is the scaling factor, T is the rotation an-
gle and c is the shift value. When the transformation
factors are estimated, node i can calculates it’s phys-
ical coordinates using the equation 7 where X is the
topological coordinates of node i and Y is the physical
coordinates of node i. Figure 3 compares the localiza-
tion error before and after the Procrustes analysis. In
this experiment, we can see that each node uses a dif-
ferent transformation factor to calculates it’s physical
coordinates. Thus the localization error has been re-
duced.
0 5 10 15 20 25 30
0
5
10
15
20
25
30
X
Y
Actual Position
Topological Coordinates
Calculated Physical Coordinates
Figure 3: Impact of Procrustes Analysis.
4 RESULT
The performance of the proposed RP-PA algorithm
is evaluated in this section. First the receive signal
strength model used for the simulation is described.
Then the performance of the algorithm is compared
with other existing algorithms. MATLAB simulation
software was used for the computations.
4.1 Receive Signal Strength Model
The received signal strength can be modeled as hav-
ing two components such as path loss and shadow-
ing (Pathirana et al., 2005). Therefore, the commonly
used propagation model of RF signals is given in
equation (8).
P
rx,i
(t) = P
tx, j
− 10εlogd
ij
(t) + v
i
(t) (8)
where, the received signal strength at node i at
time t is P
rx,i
(t), the transmitted signal strength of the
signal at node j is P
tx, j
, the path-loss exponent is ε,
the distance between node i and node j at time t is
d
ij
(t) and the logarithm of shadowing component on
node i at time t is v
i
(t).
However, this model is not suitable for a network
with some obstacles. In (Lott and Forkel, 2001), they
proposed a MultiWall-Multifloor Model for RF com-
munication. In this model the variation of the absorp-
tion against the thickness of the medium which signal
Table 1: Simulation Parameters.
Parameter Value
Transmitted power -50dB
Sensitivity -90dB
Communication radius 10m
Suburban area ε = 2.7
σ =9.6
Light tree density area ε = 3.6
σ =8.2
traverse, is not considered. Therefore we updated the
equation (8) by using the Lambert-Bouguer law. Let
L
ob,i
(t) is the loss due to signal absorption from ob-
stacles exist in the line of sight of node i and j at time
t, then the RF signal propagation model is as in equa-
tion (9).
P
rx,i
(t) = P
tx, j
− 10εlogd
ij
(t) − L
ob,i
(t) + v
i
(t) (9)
The absorption coefficient and the thickness of the
obstacle medium, which signal traverses are α and
d
o
(t) respectively. Then L
ob,i
(t) can be calculated as,
L
ob,i
(t) = Σ
n
k=1
10αd
o
(t)log(e) (10)
where, n is the number of obstacles exist in between
node i and node j.
4.2 Performance Evaluation
The performance of the receiving probability ap-
proach and other two localization approaches, that
are RSSI based(Mukhopadhyay et al., 2014) and hop
based (Dhanapala and Jayasumana, 2014), is evalu-
ated through large-scale simulations. To make the ca-
parison equitable for all three approaches, the Pro-
crustes analysis is applied to each output obtained
from the above three approaches.
The large-scale WSNs we selected for the evalua-
tion is shown in Figure 4 and 5 . Here we have dif-
ferent shapes of networks with obstacles. The Figure
4(a) is a 496 sensor nodes circular-shaped network in
a suburban area with three physical obstacles (con-
crete barriers). The Figure 5(a) is a 554 sensor nodes
network with a concave void (concrete barriers) in a
light tree density area. Table 1 presents the simula-
tion parameters. Here we consider anchor nodes are
randomly distributed over the network area.
Figure 4 and 5, clearly demonstrate the effective-
ness of the proposed algorithm. However to compare
the performance of the algorithm, we calculate the lo-
calization error as in the equation 11. Figure 6 com-
Sensor Localization using Signal Receiving Probability and Procrustes Analysis
117

0 5 10 15 20 25 30
0
5
10
15
20
25
30
X
Y
(a)
−5 0 5 10 15 20 25 30
0
5
10
15
20
25
30
X
Y
(b)
−10 0 10 20 30 40
−5
0
5
10
15
20
25
30
35
X
Y
(c)
−10 0 10 20 30 40
0
5
10
15
20
25
30
35
X
Y
(d)
Figure 4: (a) Circular-shaped network with 496 nodes , (b) Output of proposed RP-PA algorithm, (c) Output of RSSI algorithm
and (d) Output of Hop based algorithm.
0 5 10 15 20 25 30
0
5
10
15
20
25
30
X
Y
(a)
−10 0 10 20 30 40
0
5
10
15
20
25
30
35
X
Y
(b)
−5 0 5 10 15 20 25 30
0
5
10
15
20
25
30
X
Y
(c)
0 5 10 15 20 25 30
−5
0
5
10
15
20
25
30
X
Y
(d)
Figure 5: (a) Circular-shaped concave void network with 554 nodes , (b) Output of proposed RP-PA algorithm, (c) Output of
RSSI algorithm and (d) Output of Hop based algorithm.
SENSORNETS 2016 - 5th International Conference on Sensor Networks
118

pares the localization error of the three methods men-
tioned above for the two network distributions. It can
be seen that the proposed RP-PA algorithms outper-
forms the other two methods by having a average lo-
calization error less than 2m.
location
e
rror =
∑
N
i=1
p
(x
i
− x
t
i
)
2
+ (y
i
− y
t
i
)
2
N
(11)
Figure 4 Figure 5
0
2
4
6
8
10
12
Localization Error
RP−PA RSSI Hop−count
Figure 6: Localization error comparison.
Moreover, to analyze the localization error more
enormously, Figure 7 compares the cumulative distri-
bution of the localization error of three methods for
the two networks. From Figure 7(a) and Figure 7(b),
it can be seen that 80% of nodes have less than 2m
localization error with RP-PA algorithm. Hence it is
seen that RP-PA algorithm performs better than RSSI
and hop based localization algorithms.
Figure 8 shows the performance of the RP-PA al-
gorithm against the number of anchor nodes. Accord-
ing to the figure, RP-PA algorithm has been able to
generate physical coordinates of sensor nodes with
less than 2m average localization error for the two net-
work deployed in different environmental situations
using 10% of anchor nodes. Thus, with less amount
of sensor nodes, the algorithm can calculate the loca-
tion of sensors in a large-scale WSN.
5 CONCLUSION
We presented a RP-PA algorithm, which calculates
the coordinates of sensor nodes without using any
special hardware component. RP-PA algorithm ex-
tracts the advantages if range-based and range-free
localization techniques. In range-free approach, the
connectivity information is obtained by hop-count
matrix and as a result sensors can move non-zero dis-
tance without affecting the connectivity information.
However in range-based algorithms, RF communi-
cation effects such as noise, fading and interference
0 2 4 6 8 10 12
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Localization Error %
CDF of Localization Error
Empirical CDF
RP−PA
Hop−count
RSSI
(a)
0 2 4 6 8 10 12 14
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Localization Error %
CDF of Localization Error
Empirical CDF
RP−PA
Hop−count
RSSI
(b)
Figure 7: (a) CDF of localization error in Figure 4 network,
(b) CDF of localizatio error in Figure 5 network.
10 20 30 40 50
−5
0
5
10
Localization Error
Anchor Percentage %
Localization Error vs Anchor Percentage in Figure 4 network
10 20 30 40 50
−5
0
5
10
Localization Error
Anchor Percentage %
Localization Error vs Anchor Percentage in Figure 5 network
Figure 8: Localization error against the anchor percentage
with respect to the total number of nodes.
affect the range measurements. To defeat these is-
sues, we generate a topology map i.e. arrangement of
nodes, using a signal receiving probability function
that is sensitive to the distance. Then the topology co-
ordinates are transformed to the physical coordinates
using Procrustes analysis. Due the obstacles exist in
the network; the transformation is not unique through
out the whole network. Thus we calculate the trans-
formation factors in each sensor node.
The result shows that the RP-PA algorithm calcu-
Sensor Localization using Signal Receiving Probability and Procrustes Analysis
119

late physical coordinates of sensors with localization
error less than 2m and it outperforms RSSI and hop-
based localization algorithms.
ACKNOWLEDGEMENTS
This research is supported in part by National ICT
Australia (NICTA).
REFERENCES
Al Alawi, R. (2011). Rssi based location estimation in wire-
less sensors networks. In Networks (ICON), 2011 17th
IEEE International Conference on, pages 118–122.
Chengdong, W., Shifeng, C., Yunzhou, Z., Long, C., and
Hao, W. (2011). A rssi-based probabilistic distri-
bution localization algorithm for wireless sensor net-
work. In Information Technology and Artificial In-
telligence Conference (ITAIC), 2011 6th IEEE Joint
International, volume 1, pages 333–337.
Dhanapala, D. and Jayasumana, A. (2014). Topology pre-
serving maps ;extracting layout maps of wireless sen-
sor networks from virtual coordinates. Networking,
IEEE/ACM Transactions on, 22(3):784–797.
Garca-Hernndez, C., Ibargengoytia-Gonzlez, P., Garca-
Hernndez, J., and PrezDaz, J. (2007). Wireless sensor
networks and applications: a survey. pages 264–273.
Gholami, M., Gezici, S., and Strom, E. (2012). Improved
position estimation using hybrid tw-toa and tdoa in co-
operative networks. Signal Processing, IEEE Trans-
actions on, 60(7):3770–3785.
Huang, B., Xie, L., and Yang, Z. (2015). Tdoa-based source
localization with distance-dependent noises. Wireless
Communications, IEEE Transactions on, 14(1):468–
480.
Kotwal, S., Verma, S., Suryansh, S., and Sharma, A.
(2010). Region based collaborative angle of arrival
localization for wireless sensor networks with max-
imum range information. In Computational Intelli-
gence and Communication Networks (CICN), 2010
International Conference on, pages 301–307.
Liu, C., Wu, K., and He, T. (2004). Sensor localization with
ring overlapping based on comparison of received sig-
nal strength indicator. In Mobile Ad-hoc and Sen-
sor Systems, 2004 IEEE International Conference on,
pages 516–518.
Liu, S., Tang, Y., Zhang, C., and Yue, S. (2012). Self-
map building in wireless sensor network based on tdoa
measurements. In Multisensor Fusion and Integration
for Intelligent Systems (MFI), 2012 IEEE Conference
on, pages 150–155.
Lott, M. and Forkel, I. (2001). A multi-wall-and-floor
model for indoor radio propagation. In Vehicu-
lar Technology Conference, 2001. VTC 2001 Spring.
IEEE VTS 53rd, volume 1, pages 464–468 vol.1.
Luo, X. L., Li, W., and Lin, J. R. (2012). Geometric loca-
tion based on tdoa for wireless sensor networks. ISRN
Applied Mathematics, 2012.
Mukhopadhyay, B., Sarangi, S., and Kar, S. (2014). Novel
rssi evaluation models for accurate indoor localization
with sensor networks. In Communications (NCC),
2014 Twentieth National Conference on, pages 1–6.
Nhat, V. D. M., Vo, N., Challa, S., and Lee, S. (2008). Non-
metric mds for sensor localization. In Wireless Perva-
sive Computing, 2008. ISWPC 2008. 3rd International
Symposium on, pages 396–400.
Niculescu, D. and Nath, B. (2003). Dv based positioning in
ad hoc networks. In Kluwer journal of Telecommuni-
cation Systems, volume 22, page 267280.
Oguz-Ekim, P., Gomes, J., Oliveira, P., Reza Gholami, M.,
and Strom, E. (2013). Tw-toa based cooperative sen-
sor network localization with unknown turn-around
time. In Acoustics, Speech and Signal Processing
(ICASSP), 2013 IEEE International Conference on,
pages 6416–6420.
Pathirana, P., Bulusu, N., Savkin, A., and Jha, S. (2005).
Node localization using mobile robots in delay-
tolerant sensor networks. Mobile Computing, IEEE
Transactions on, 4(3):285–296.
Savarese, C., Rabaey, J., and Langendoen, K. (2002).
Robust positioning algorithms for distributed ad-hoc
wireless sensor networks. USENIX Annual Technical
Conference, pages 317–327.
Tian, H., Huang, C., Blum, B. M., Stankovic, J., and Ab-
delzaher, T. (2003). Range-free localization schemes
for large scale sensor networks. In Proceedings of the
9th Annual International Conference on Mobile Com-
puting and Networking, MobiCom ’03, pages 81–95.
Tubaishat, M. and Madria, S. (2003). Ieee potentials. pages
20–23.
Wang, Y. and Ho, K. (2013). Tdoa source localization in
the presence of synchronization clock bias and sensor
position errors. Signal Processing, IEEE Transactions
on, 61(18):4532–4544.
Wanga, X., Yuanb, S., Laura, R., and Langb, W. (2011).
Dynamic localization based on spatial reasoning with
rssi in wireless sensor networks for transport logistics.
In Sensors and Actuators, pages 421–428.
Wymeersch, H., Lien, J., and Win, M. (2009). Cooperative
localization in wireless networks. Proceedings of the
IEEE, 97(2):427–450.
Zhang, H., Zhang, J., and Wu, H. (2012). An adaptive local-
ization algorithm based on rssi in wireless sensor net-
works. In Cloud Computing and Intelligent Systems
(CCIS), 2012 IEEE 2nd International Conference on,
volume 03, pages 1133–1136.
SENSORNETS 2016 - 5th International Conference on Sensor Networks
120
