Pattern Recognition in Real Time using Neural Networks:
An Application for Pressure Measurement
Parham Piroozan
Department of Mechanical Engineering, California State Polytechnic University, 3801 W Temple Ave, Pomona, CA 91768,
U.S.A.
Keywords: Real-time Recognition of Fringe Patterns, Neural Networks, Interferometric Reflection Moiré, Pressure
Sensor, Electro-optic System.
Abstract: Retrieving information in real time from fringe patterns is a topic of great importance in scientific and
engineering applications of optical methods. This paper describes an application of neural networks for real
time pressure measurement using fringe pattern recognition. It is based on the capability of neural networks
to recognize signals that are similar but not identical to the signals which were used to train the network. In
this investigation a pressure sensor, which was part of the wall of the wind tunnel, and an optical apparatus
were used to produce moiré fringes. The fringe patterns generated were analyzed by a back propagation neural
network at the speed of the recording device, which was a CCD camera with a pixel resolution of 649 (H) x
491 (V). This method of information retrieval was used to measure the pressure fluctuations in the boundary
layer flow. A second neural network was used to recognize the pressure patterns and to provide input to a
control system that was capable to preserve the stability of the flow.
1 INTRODUCTION
Determination of frequency in fringe patterns is of
great importance in many applications of optical
methods in engineering (Sciammarella and Kim,
2005). This paper presents a technique to find fringe
pattern frequencies in real-time. Real-time refers to
timing within the range of frequencies of the
recording devices such as CCD cameras. In this
paper, an optical pressure sensor, which is capable of
producing moiré fringes, is introduced. The optical
pressure sensor was part of the wall of the wind tunnel
and was used to instantaneously measure the pressure
fluctuations in the boundary layer flow. The optical
apparatus used was a reflection moiré interferometer.
The Helium-Neon laser light was used to illuminate
the reflecting surface of the pressure sensor, which
was displaced due to wall pressure fluctuations by a
few light wavelengths. A CCD camera recorded
instantaneous fringe patterns. These fringes were
slope fringes which were used for the pressure
measurements by a back propagation neural network.
The wall area observed was approximately 76 mm x
76 mm. The flow velocity outside the boundary layer
was 6.2 m/sec. Wall pressure was both positive and
negative and was in the order of ± 5.0 x 10
-4
psi
(Piroozan, 1997).
In the moiré interferometer developed in the
present investigation, slope of the deformed
membrane generated straight and vertical (constant
slope) moiré fringes, which were linearly
proportional to the pressure on the membrane, and
were the source of information used for the wall
pressure measurement.
The optical system provided 15 x 15 arrays of
inputs corresponding to the 15 x 15 array of
diaphragms of the pressure sensor to a back
propagation neural network that analyzed the
received signals and classified them into four pressure
levels. The classified pressures were a 15 x 15 array
of numbers ranging from 1 to 4. These numbers were
then input to a second back propagation neural
network which was used to recognize the pressure
patterns. The output from the back propagation
neural network used for pattern recognition provided
real-time input to a control system for fluid flow
control. Figure 1 shows a schematic representation of
the main components used in the neural network
reading process.
566
Piroozan, P.
Pattern Recognition in Real Time using Neural Networks: An Application for Pressure Measurement.
DOI: 10.5220/0005673105660572
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 566-572
ISBN: 978-989-758-173-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Schematic representation of the neural network
reading process.
2 PRESSURE SENSOR
The optical pressure transducer was based on
measuring the slopes of an array of diaphragms using
a moiré interferometer. The diaphragms were formed
by stretching an elastic membrane over an array of
holes drilled on a circular disk, which was set into the
boundary layer flow (Figure 2) (Piroozan, 1997).
A 15 x 15 array of holes each with a diameter of 4
mm and center-to-center distance of 5 mm were
drilled through the disk. The diameter and spacing of
the holes were selected to give a spatial resolution of
φ
6 mm
15 x 15 Array of 4 mm dia. holes,
center to center 5 mm
Beveled edge, 8°
Static pressure chamber
wall, 105 mm inner x
140 mm outer dia.
φ
4 mm
‘O’ Ring groove
110 mm inner x
120 mm outer
dia.
Support flange 140 mm
inner x 170 mm outer dia.
Figure 2: Pressure sensor layout.
approximately 4 holes per span-wise wavelength of
the stream-wise vortex mode in the experiment. The
holes were spaced evenly in the span-wise and
stream-wise directions. These holes collectively
made a square, 76.5 mm in width and 74 mm in
height, which was illuminated by a light beam with a
diameter of 105 mm.
The measuring (front) surface of the disk was
covered with a thin layer of cellulose nitrate
(nitrocellulose) membrane covered with a thin layer
of aluminum. It formed an optical quality mirror
surface, which was part of a moiré interferometer.
Figure 3 shows a computer generated pressure field
used for implementing the required software. This
Figure shows the moiré fringe patterns for each of the
15 x 15 array of diaphragms of the pressure sensor
(Figure 2) for a pressure ranging between ±5.0 x 10
-4
psi.
3 OPTICAL ARRANGEMENT
Figure 4 shows the shear interferometer used for the
wall pressure measurement. The optical arrangement
was mounted on a steel structure beside the wind
tunnel. A 10.0 milliwatt linearly polarized Helium
Neon laser was used as the light source. Diameter of
the laser beam was expanded from 0.95 mm to 150
mm by using: a microscope objective with a
magnification of 63x and focal length of 2.94 mm, a
5 μm pinhole,
Figure 3: Simulated pressure field used to develop the
software of the pressure sensing system.
and a collimating lens with a focal length of 762 mm
(30 inches) and diameter of 152 mm (6 inches).
Collimated light passed through a 1000 line/inch
grating and was reflected by the pressure sensor after
passing through a non-reflecting, optically flat glass
with a diameter of 279 mm (11 inches) which was
mounted on the wind tunnel wall. Reflected light then
passed through the non-reflecting glass and then a
telecentric system of lenses. The telecentric system
of lenses consisted of two identical lenses with focal
Air
Flow
Flexible Wall
ΔP(X,Y)
Pressure Sensor
Actuator
Electro-Optic
Signal Gathering and
Processing System
X
Y
Pattern Recognition in Real Time using Neural Networks: An Application for Pressure Measurement
567

600 mm
600 mm
Flow
direction
Wind tunnel wall
Non reflecting glass
Lens L
3
Grating 2
Pressure sensor
Collimating
lens
Laser source
Spatial
filte
r
Gratin
g
1
d = 40 mm
CCD camera
Lens L
1
Lens L
2
13
o
Image plane
152 mm
762 mm
65 mm
600 mm
45 mm
120 mm
13
o
Figure 4: Optical setup used for creating moiré fringes.
lengths of 600 mm and diameters of 120 mm which
reproduced the pressure sensor at the focal point of
the second lens. The second grating was placed after
the telecentric system of lenses and was identical with
the first grating with a frequency of 1000 line/inch.
This grating was placed at a distance d from the focal
point of the second lens of the telecentric lens system,
where the pressure sensor was reproduced.
Sensitivity was increased by increasing the distance
d. The third lens used had a focal length of 128.7 mm
and diameter of 76 mm which was used to focus the
fundamental harmonic (order +1 or -1) and order 0
into the CCD camera. This was done by slightly
rotating lens L
3
about its vertical axis.
Figure 5 shows the elastic membrane stretched
over a pressure sensor. Slope of the membrane is
given by (Piroozan, 1997),
Figure 5: Elastic membrane stretched over a pressure
sensor.
o
2T
Prw
=
r
∂
∂
(1)
where P is the pressure differential over the
membrane, T
o
is the tension in the membrane, and r is
the distance measured from the center of each sensor.
Equation (1) shows that fringes are a linear function
of the pressure differential over the membrane.
Figure 6 shows the constant slope moiré fringes
recorded using the optical setup shown in Figure 4 for
a 3 x 3 version of the pressure sensor (Ligtenberg,
1955).
4 PRESSURE LEVELS
MEASUREMENT: NEURAL
NETWORKS
For the complete process of flow control, the sensor
had to measure the pressure at the 225 points defined
by the 15 x 15 array of membranes in one cycle, that
is in 1/30 second (33 milliseconds). There is no time
to apply methods of fringe analysis to obtain the
pressure values. For this reason a back propagation
neural network was selected to read the patterns and
to classify the readings in real time into pressures. A
back propagation network can be used for the purpose
of recognizing signals similar but not totally identical
to those which have been used for training the
network. The architecture of the network is
illustrated in Figure 7: there is an input layer, an
output layer, and a hidden layer, all interconnected.
The training of a feedback network requires three
stages: (a) feed forward of the patterns used for the
training, (b) determination of error terms at each node
via the back propagation strategy, and (c) adjustment
of the weights. In the recognition phase of the
network only the forward part is applied, hence the
results may be very fast (Fausett, 1994).
Figure 6: Constant slope moiré fringes recorded over a 3 x
3 version of the pressure sensor.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
568

-50 x 10
--5
psi
*
-45 x 10
--5
psi -40 x 10
--5
psi -35 x 10
--5
psi -30 x 10
--5
psi
Pressure Level 1
-25 x 10
--5
psi -20 x 10
--5
psi -15 x 10
--5
psi -10 x 10
--5
psi -5 x 10
--5
psi
Pressure Level 2
5 x 10
--5
psi 10 x 10
--5
psi 15 x 10
--5
psi 20 x 10
--5
psi 25 x 10
--5
psi
Pressure Level 3
30 x 10
--5
psi 35 x 10
--5
psi 40 x 10
--5
psi 45 x 10
--5
psi 50 x 10
--5
psi
Pressure Level 4
Figure 8: Simulated pressure patterns (levels 1 and 2 correspond to negative pressures, levels 3 and 4 correspond to positive
pressures).
Figure 7: Schematic representation of the back propagation
network utilized to classify and read fringes.
The accuracy of the obtained results depends on the
training phase of the network. The same circuit will
provide different results with different trainings.
There are two important goals to fulfill in the design
of the network:
a) All expected classes of inputs must be represented
in the training process. The separation between
classes must be adequately represented.
b) Within each class, all the possible variations must
be present.
The size of the required training samples depends
on the size of the network. There is a rule of thumb
of having at least twice as many samples as the
number of weights present in the network.
The input to the system is a series of calibration
patterns. Two types of calibrations were performed
in this particular application: static and dynamic
calibrations. In the static calibration, pre-selected
pressures were applied to the sensors, the images
were recorded and stored in the computer memory.
The dynamic pressure calibration was utilized to
verify the static calibration and to see if there is any
dynamic resonant effect in the patterns. The static
calibration patterns were utilized as input for the
neutral network. Figure 8 shows a computer-
generated set of calibration pressures used in the
preliminary developments of the system. In this
preliminary work, the whole process was digitally
simulated. The levels of pressure were subdivided
into four levels with the limits indicated in Figure
8.To analyze the pressure distribution in a given
region, an array containing a number of equally
spaced sensors is utilized. Each sensor gives the
average pressure in a region (area of the sensor). This
area is selected by considerations involving the
physical size of the structures in the flow that one
wants to detect, the sensibility of the individual
sensors, the CCD camera sensor size, the number of
pixels, and the optical system.
Figure 3 showed a computer-generated pressure
field used for implementing the required software.
Figure 9 shows the output matrix corresponding to the
patterns of Figure 3. The neural networks software
used to carry out this operation was NeuralWorks
Professional II/Plus (NeuralWare Inc.).
For purposes of comparing experimental (hot
wire) measurements and numerical computation
values, pressure measurements were done for a 1 x 7
array of the pressure sensor. 1,050 fringe patterns
4 2 2 1 2 1 1 1 1 1 2 1 1 2 2
3 2 2 2 1 1 2 1 1 1 1 2 2 2 2
2 1 2 2 1 1 1 2 1 1 1 1 2 1 2
4 4 4 4 4 3 4 3 4 3 4 4 4 3 4
4 3 3 4 4 4 4 4 4 4 3 4 4 4 3
4 4 3 4 3 3 4 4 4 4 4 3 4 4 3
1 1 2 2 1 1 2 2 2 2 2 2 2 1 1
1 2 1 2 1 1 1 2 1 1 1 1 1 1 1
1 1 2 1 2 2 1 1 2 2 1 1 2 1 1
4 4 4 3 4 4 4 4 3 4 3 4 4 4 4
4 3 3 2 3 3 4 4 4 4 4 3 4 3 4
4 4 3 4 3 3 4 3 2 4 3 3 3 4 4
1 1 2 2 1 1 1 2 1 1 1 1 2 1 1
1 1 2 1 1 1 1 1 1 1 1 1 2 1 1
1 1 2 2 1 1 1 1 1 2 1 1 1 1 1
Figure 9: Output of the neural network corresponding to the
pressure field shown in Figure 3.
Hidden layer
Input layer
Output layer
1
x
x
x
x
x
j
y y y y
y
i
z
1
z
2
z
3
z
k
Pattern Recognition in Real Time using Neural Networks: An Application for Pressure Measurement
569

1 2 3 4 5
1 2 3 4 5 6 7 8 9 10
from the array with known pressures in the range of
±0.0005 psi were recorded. Each record consisted of
24 positive integers ranging from zero to 255 which
were the minimum and maximum pixel values in an
eight-bit frame. These numbers were input to a back
propagation neural network with 24 processing
elements in the input layer. Figure 10 shows the input
to the back propagation neural network from each
individual sensor.
1 2 3 4 5 .................. 22 23 24
Processing elements
in the input layer
1 2 3 4 5 ............................................. 22 23 24
Pixels
Pixel
Sensor area
Figure 10: Input data from a sensor to the input layer of the
back propagation neural network for pressure classification.
Number of samples were doubled by writing the
input vector in normal {a
1
, a
2
, a
3
, ... , a
24
} as well as
in reverse order {a
24
, a
23
, a
22
, ... , a
1
}, where a
represents the pixel value. By doing so, not only the
number of samples was increased, but also phase
differences arising from the different sensors and
possible noise were also included. These patterns
were used to train and test the back propagation
neural network. 1,750 of the records (out of the total
of 2,100) were used for training while the remaining
350 records were used to test the performance of the
network. The network consisted of an input layer,
one output layer, and one hidden layer as shown in
Figure 11.
Figure 11: The back propagation neural network used for
the pressure classification.
There were 24 processing elements in the input
layer, ten processing elements in the hidden layer, and
five processing elements in the output layer which
were fully interconnected (connections are not shown
in Figure 11). The input consisted of positive integers
ranging from zero to 255. The input data was first
mapped to lie between +1 and -1 (bipolar format) by
selecting the “Bipolar Inputs” and “MinMax Table”
Figure 12: RMS error of the back propagation network used
for pressure classification.
options from the neural networks software
(NeuralWare, 1993). The “SoftMax Output” option
was also used to force the components of the desired
output to add up to one (one of n code). The tangent
hyperbolic function was used as the activation
function while normalized cumulative delta rule was
used as the learning rule. Compared to other
activation functions such as sine or sigmoid
functions, tangent hyperbolic gave better results.
Epoch was also set to 350, which was approximately
the number of training records in each pressure level.
By doing so, weights were updated after 350 learning
cycles. This resulted in a better performance by the
network as compared to selecting 1750 (total number
of training records) or using the default setting value
of 16. Figure 12 shows the Root Mean Square (RMS)
error during the training session (RMS error is a
common measure of the performance of a network).
The RMS error adds up the squares of the errors for
each processing element in the output layer, divides
by the number of processing elements in the output
layer to obtain an average value, and then takes the
square root of that average value. The network ceased
to learn after the RMS error converged to
approximately 0.10. This may be in part due to
inaccuracies in the input data used for training the
network. Inaccuracies are mainly due to the pressure
fluctuations in the air in the lab which is of the same
order of magnitude as the pressures set for calibration.
Output (pressure levels
1, 2, 3, 4, or 5)
Hidden
layer
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Input (gra
y
levels 0 to
255)
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
570

(a) (b) (c)
Figure 14: (a) Computer generated pressure field, and the (b) corresponding classified pressure field output from neural
networks. (c) output signals from pattern recognition neural networks.
Figure 12 shows that the RMS error has converged
during the learning session, which means that input
patterns are learned by the network in spite of the
inaccuracies in the input data. In testing, the trained
network gave 56 mistakes out of the 350 records used
for testing (testing was done by pressure patterns with
known pressure levels), that is, 84% correct answers.
The source code generated from the trained network
was then used for the real pressure classification.
To make the operation fast, data from only one
row of each pressure sensor was used for the pressure
measurement. Each row was represented by 24 pixels
per sensor. Images were frozen during the data
acquisition process. Analysis was done sequentially
for each sensor. The output was a 1 x 7 array
consisting of integers 1 through 5 corresponding to
the five pressure levels.
5 PROCESS TO ANALYZE THE
PRESSURE PATTERNS
The pressure pattern is characterized by elongated
features, vortices, in the direction of the flow. In the
transversal direction these features are of the order of
three sensor spacing wide. Through theoretical and
experimental results the shape of the features is
known and only actual dimensions (width and
position of the longitudinal vortices) are not known.
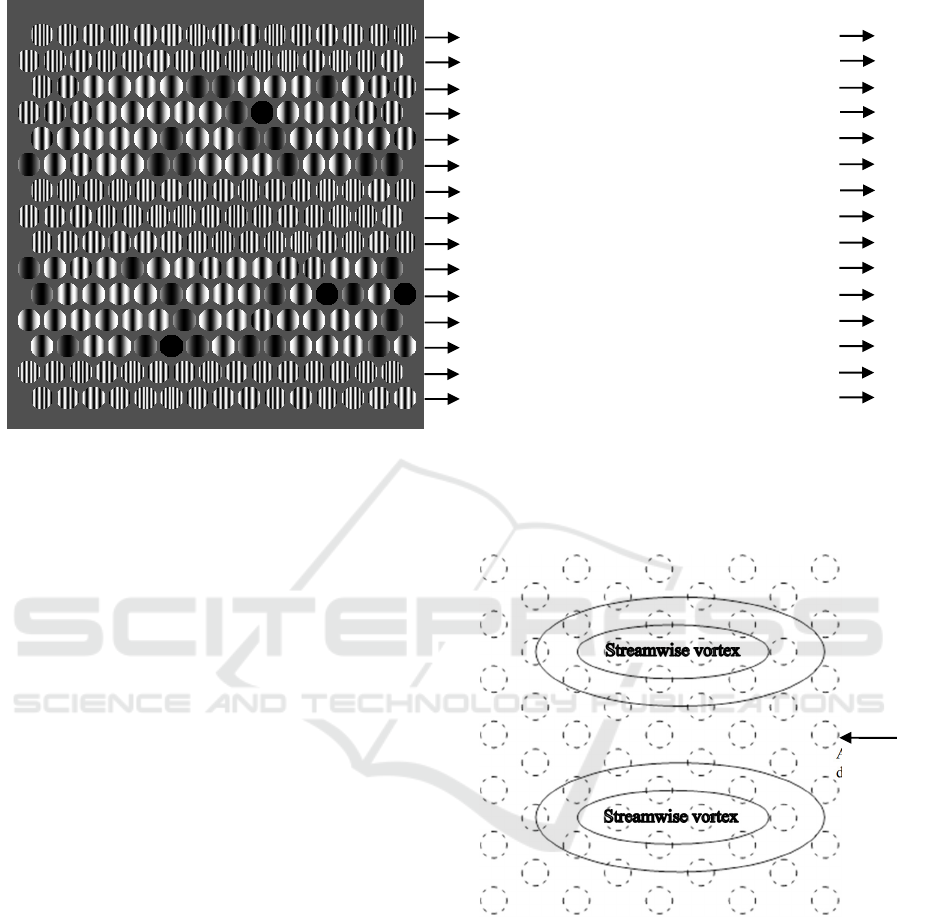
Figure 13 shows the expected pressure field.
Figure 13: The expected pressure field.
The complete process of pressure measurement
and pattern recognition was done by using computer
generated and expected pressure fields for the 15 x 15
array of sensors. Figure 14 shows a sample of the
computer generated pressure field with the
corresponding output from the back propagation
neural networks for pressure classification and
pattern recognition. Pressures were classified into
four levels. The back propagation neural network
used for pressure pattern recognition consisted of an
input layer with 225 processing elements, a hidden
layer with 50 processing elements and an output layer
Airflow
direction
4 4 3 4 3 3 4 3 2 4 3 3 3 4 4
4 4 3 4 3 3 4 4 4 4 4 3 4 4 3
4 2 2 1 2 1 1 1 1 1 2 1 1 2 2
3 2 2 2 1 1 2 1 1 1 1 2 2 2 2
2 1 2 2 1 1 1 2 1 1 1 1 2 1 2
1 1 2 2 1 1 1 1 1 2 1 1 1 1 1
4 4 4 4 4 3 4 3 4 3 4 4 4 3 4
4 3 3 4 4 4 4 4 4 4 3 4 4 4 3
4 3 3 2 3 3 4 4 4 4 4 3 4 3 4
1 1 2 2 1 1 2 2 2 2 2 2 2 1 1
1 2 1 2 1 1 1 2 1 1 1 1 1 1 1
1 1 2 1 2 2 1 1 2 2 1 1 2 1 1
1 1 2 1 1 1 1 1 1 1 1 1 2 1 1
4 4 4 3 4 4 4 4 3 4 3 4 4 4 4
4 3 3 4 4 4 4 3 3 4 3 4 4 3 3
1
1
0
0
0
0
1
1
1
0
0
0
0
1
1
Pattern Recognition in Real Time using Neural Networks: An Application for Pressure Measurement
571

with 15 processing elements. The training patterns
with the desired output vectors were used to train the
back propagation neural network. “Delta-Rule” and
“Sigmoid” function were used as the learning rule and
the activation function. “Bipolar Inputs” was
deselected and Epoch was selected as 16. After about
5,000,000 iterations, the training set converged and
the network was tested with the patterns that the
network had not seen before (these patterns were not
used for training the network). The 15 outputs from
the network were exactly the same as the desired
output vectors as shown in Figure 14 (c).
6 CONCLUSIONS
From the obtained patterns it can be concluded that
the back-propagation neural network used for pattern
classification and pressure measurement proved to
work satisfactorily especially for noisy inputs.
Pressure fluctuations in the boundary layer were
extremely small in the order of ±5.0 x 10
-4
psi. When
dealing with small pressures, calibration (gathering
the training and testing data) proved to be a problem
due to very small random fluctuations in the
atmospheric pressure in the laboratory due to external
causes (wind blowing, opening or closing doors in
neighboring rooms). Calibration and data gathering
must be done with static pressures applied to the
pressure sensor with no pressure fluctuations present
in the surrounding air.
Successful operation of the pressure classification
and pattern recognition to a large extend depends on
the quality of the fringe patterns and the signals
generated by the electro-optical system, in particular,
the pressure sensor. Great care must be taken in the
selection and fabrication of the membrane material.
The computer code used for the pattern
recognition of the 15 x 15 array consists of
approximately 6000 lines of C programming.
Operating systems such as Windows or DOS and C
compilers running on these platforms are not
adequate, or, can handle this job very slowly. It is
recommended to operate the image processing system
and the neural networks on work stations with UNIX
operating system.
Determination of fringe pattern frequencies in real
time has a variety of interesting applications in the
future as viewed from the recent developments
(Sciammarella and Kim, 2005). Neural networks
proved to be a powerful tool which can be utilized for
this purpose.
ACKNOWLEDGEMENTS
The research work presented in this paper was done
in collaboration with Dr. Cesar A. Sciammarella,
Professor of the Department of Mechanical,
Materials, and Aerospace Engineering, Illinois
Institute of Technology, USA, and Dr. Thomas
Corke, Clark Chair Professor of the Department of
Mechanical and Aerospace Engineering, Notre Dame
University, USA. To them goes my deep appreciation
and recognition for their innumerable contributions to
the project.
REFERENCES
Sciammarella, C.A., Kim, T., 2005. Frequency modulation
interpretation of fringes and computation of strains. In
Experiemntal Mechanics 2005;45:393-403.
Sciammarella, C. A., Piroozan, P., 2007. Real-time
determination of fringe pattern frequencies: An
application to pressure measurement. In Optics and
Lasers in Engineering 45 (2007) 565-577.
Piroozan, P., 1997. Pressure sensor to determine spatial
pressure distribution in boundary layer flows. Ph.D.,
Illinois Institute of Technology.
Emmerling, R., 1973. The instantaneous structure of the
wall pressure under a turbulent boundary layer flow.
Max-Planck-Institut Fur Stromungsforschung,
Gottingen, Bericht Nr. 9.
Dinkelacker, A., Hessel, M., Meier, G. E. A., Schewe, G.,
1977. Investigation of pressure fluctuations beneath a
turbulent boundary layer by means of an optical
method. In The Physics of Fluids, Vol. 20, No. 10, Pt.
11.
Ligtenberg, F. K., 1955. The moiré method and new
experimental method in the determination of moments
in small slab models. In Proceedings of the Society of
Experimental Stress Analysis, V, XII, No. 2, pp. 82-98.
Fausett, L., 1994. Fundamentals of Neural Networks:
Architectures, Algorithms, and Applications. Prentice
Hall, Englewood Cliffs, New Jersey.
Freeman, J. A., Skapura, D. M., 1992. Neural Networks:
Algorithms, Applications, and Programming
Techniques. Addison-Wesley Publishing Company,
Inc. Massachusetts.
Masters, T., 1993. Practical Neural Network Recipes in
C++. Academic Press, Inc. San Diego, CA.
Masters, T., 1994. Signal and Image Processing with
Neural Networks: A C++ Sourcebook. John Wiley &
Sons, Inc. New York.
NeuralWare, 1993. Neural Computing, A Technology
Handbook for Professional II / Plus and NeuralWorks
Explorer. NeuralWare, Inc. Technical Publications
Group. Pittsburgh, PA.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
572