Non-linear Distance-based Semi-supervised Multi-class Gesture

Recognition

Husam Al-Behadili

1,2

, Arne Grumpe

and Christian W

ohler

Electrical Engineering, University of Mustansiriyah, Al-Mustansiriyah, Box 46007, Baghdad, Iraq

Image Analysis Group, TU Dortmund University, Otto-Hahn-Str. 4, D–44227, Dortmund, Germany

Keywords:

Data Stream, Nearest Class Mean, Incremental Learning, Semi-supervised Learning, Kernel.

Abstract:

The automatic recognition of gestures is important in a variety of applications, e.g. human-machine-

interaction. Commonly, different individuals execute gestures in a slightly different manner and thus a fully

labelled dataset is not available while unlabelled data may be acquired from an on-line stream. Consequently,

gesture recognition systems should be able to be trained in a semi-supervised learning scenario. Additionally,

real-time systems and large-scale data require a dimensionality reduction of the data to reduce the processing

time. This is commonly achieved by linear subspace projections. Most of the gesture data sets, however, are

non-linearly distributed. Hence, linear sub-space projection fails to separate the classes. We propose an ex-

tension to linear subspace projection by applying a non-linear transformation to a space of higher dimensional

after the linear subspace projection. This mapping, however, is not explicitly evaluated but implicitly used by

a kernel function. The kernel nearest class mean (KNCM) classiﬁer is shown to handle the non-linearity as

well as the semi-supervised learning scenario. The computational expense of the non-linear kernel function

is compensated by the dimensionality reduction of the previous linear subspace projection. The method is

applied to a gesture dataset comprised of 3D trajectories. The trajectories were acquired using the Kinect

sensor. The results of the semi-supervised learning show high accuracies that approach the accuracy of a fully

supervised scenario already for small dimensions of the subspace and small training sets. The accuracy of the

semi-supervised KNCM exceeds the accuracy of the original nearest class mean classiﬁer in all cases.

1 INTRODUCTION

The recognition of gestures has become an impor-

tant element of human-machine interaction. Since the

amount of available gesture data is small and does

not cover all possible manners of performing a ges-

ture, the classiﬁcation system may beneﬁt from semi-

supervised learning to adapt to new users. A large

amount of unlabelled gesture data may be available

or acquired on-line. Semi-supervised learning, i.e.

pre-training the classiﬁer on a supervised dataset and

updating the training set using the labels assigned by

the classiﬁer (Zhu and Goldberg, 2009), solves these

problems in different applications of machine learn-

ing. However, the problems arising here are possibly

non-linearly separable distributions of the data, high

dimensionality, computational complexity of classi-

ﬁer retraining and potentially false labels assigned

by the classiﬁer that will effect the performance of

the classiﬁer after the next training cycle. Hence, it

is desirable to design a system that may operate us-

ing low-dimensional subspace projections of the data

while still being able to separate non-linearly separa-

ble data distributions with high accuracy to guaran-

tee the success of the semi-supervised learning. This

work focuses on the recognition of emblematic ges-

tures which are performed in 3D space with one arm

and acquired with a Kinect sensor.

1.1 Related Work

Metric learning is an important concept for both unsu-

pervised and semi-supervised learning. Examples of

metric learning are k-nearest neighbour (kNN) (Guil-

laumin et al., 2009; Cover and Hart, 1967; Boiman

et al., 2008; Altman, 1992), prototype learning with

adaptive distance metric (Schneider et al., 2009),

Nearest Class Mean (NCM) (Webb, 2003), and Near-

est Class Mean Multi-class Loistic Discrimination

(NCMC) (Mensink et al., 2013a,b). A kNN classiﬁer

determines the distance between a sample to be clas-

siﬁed and each training sample. The method proposed

282

Al-Behadili, H., Grumpe, A. and Wöhler, C.

Non-linear Distance-based Semi-supervised Multi-class Gesture Recognition.

DOI: 10.5220/0005674102800286

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 282-288

ISBN: 978-989-758-175-5

by Schneider et al. (2009) provides a representation of

the training set based on prototype vectors and assigns

a sample to a class based on an appropriately cho-

sen or learned distance metric. In the NCM method

suggested by Webb (2003), the Mahalanobis distance

between the query sample and the class-speciﬁc sam-

ple mean vectors measures the similarity between the

query sample and the classes. The NCMC framework

extends the NCM method applying an optimal projec-

tion that enforces the samples within the same class

to have a smaller distance to its corresponding class

mean than samples from other classes (Mensink et al.,

2013a,b).

1.2 Contribution

The performance of the classiﬁer in semi-supervised

learning scenarios is very sensitive to the classiﬁer ac-

curacy in the previous classiﬁcation process. Hence,

we need to build a classiﬁer that is robust against

outliers, has high accuracy, and is quickly retrained

in near constant time. The NCMC classiﬁer pro-

posed by Mensink et al. (2013a) uses a linear sub-

space projection approximating the covariance matrix

to reduce the computational complexity of modern

high-dimensional classiﬁcation problems. Most ges-

ture datasets, however, are are not linearly separable.

We extend the NCMC towards linearly unseparable

datasets by applying the kernel trick to improve the

performance of the NCMC in such environments and

make it less sensitive to the dimensionality of the data.

To avoid an increased runtime, the kernel function is

applied after the linear subspace projection. The pro-

posed algorithm shows an increased accuracy in both

linear and non-linear system as well as a reduced time

of processing in most cases.

2 FUNDAMENTALS

2.1 Non-linear Nearest Class Mean with

Multiple Class Centroid (NCMC)

The nearest class mean classiﬁer implemented by

Mensink et al. (2013a) looks for the closest centroid

of class c to assign the corresponding class label to

the instance with feature vector x of dimensionality

D. If we have a new sample x, the distance between

this sample and the centroid µ

of class c is d(x, µ

This new sample is labelled by ˆc, corresponding to the

class with the minimum distance among the distances

from N

classes

classes to this sample:

ˆc = argmin

c∈

{

1,...,N

classes

}

d(x, µ

). (1)

The centroid of class c is the mean of the N

instances

of class c:

∑

i=1

. (2)

The squared Mahalanobis distance speciﬁed by the

covariance matrix M

M, i.e.

d(x, µ

) = (x − µ

)

M(x − µ

), (3)

was applied by Mensink et al. (2013a). Further-

more, it is assumed by Mensink et al. (2013a) that

M = W

W , since M

M is a positive semi-deﬁnite ma-

trix. The matrix W

W ∈ R

h×D

is a low-rank metric and

h ≤ D is the effective dimension of the subspace pro-

jection. Consequently,

d(x, µ

) = (x − µ

)

W (x − µ

)

W x −W

W µ

. (4)

The posterior of the class c given an instance x is

deﬁned by Mensink et al. (2013a) as

p(c|x) =

exp



−

d(x, µ

)



classes

∑

˜c=1

exp



−

d(x, µ

˜c

)



(5)

assuming uniformly distributed classes and a

normally distributed likelihood, i.e. p(x|c) =

N (µ

W ). The covariance W

W is shared across

all classes. The log-posterior of the correct prediction

is maximized using a stochastic gradient descent to

obtain the optimal projection matrix W

W (Mensink

et al., 2013a).

For non-linear spaces, the single centroid of each

class is replaced by Mensink et al. (2013a) by multi-

ple prototypes, which are obtained using the k-means

algorithm. The query samples are then assigned to the

class of the nearest centroid. Assuming a mixture of

normal distributions centred at the N

centroids

c, j

, j ∈

{

1, . . . , N

centroids

}

for each class c, the poste-

rior probability of class c is deﬁned by Mensink et al.

(2013a) as

p(c|x) =

centroids

∑

j=1

p(m

c, j

|x), with (6)

p(m

c, j

|x) =

exp



−

d(x, m

c, j

)



classes

∑

c=1

centroids

∑

j=1

exp



−

d(x, m

)



. (7)

2.2 Kernel based Metrics

Kernels are proposed to solve non-linear separation

problems in different types of machine learning algo-

rithms. As described in detail by Theodoridis et al.

Non-linear Distance-based Semi-supervised Multi-class Gesture Recognition

283

Figure 1: Kernel trick. By transforming the original

space (left) into a space of increased dimension (right) the

two classes circle and square become linearly separable.

Adapted from Elmezain et al. (2009).

(2010), the transformation ϕ

ϕ : R

× R −→ R

a generally non-linear transformation of the feature

space R

to a space R

of increased dimension

H . Due to the transformation ϕ

ϕ, a linear separation,

i.e. a separating hyperplane, in R

becomes a non-

linear separating function when projected back onto

the original feature space. Consequently, the classes

may become linearly separable after the transforma-

tion into the space of increased dimension. An exam-

ple is shown in Fig. 1.

Commonly, it is sufﬁcient to compute inner prod-

ucts in the higher dimensional space, e.g. computing

the Euclidean distance of samples from the separating

hyperplane. The so-called “kernel Trick” utilizes this

fact. As shown by Theodoridis et al. (2010), if the

mapping of the vectors x and

x satisﬁes Mercer’s the-

orem it is not required to evaluate or know the map-

ping ϕ

ϕ, and the inner product may be replaced by the

kernel function

K(x,

x) =

ϕ(x), ϕ

ϕ(

= ϕ

ϕ(x)

ϕ(

x). (8)

Consequently, it is possible to evaluate the inner prod-

uct in the high dimensional space by applying a pos-

sibly non-linear kernel function K(x,

x) to the repre-

sentations x and

x in the original space. Examples of

common kernel functions are polynomial kernels or

Gaussian kernels (Theodoridis et al., 2010). In this

work, the kernel function is a radial basis function

(RBF) of Gaussian shape given by

RBF

(x,

x) = exp

−

x −

(2σ

)

, (9)

where σ denotes the predeﬁned width of the ker-

nel function. The Gaussian RBF kernel is shift-

invariant. Consequently, the similarity metric learned

using RBF kernels will be coordinate-independent

(Kung, 2014).

3 PROPOSED KERNEL NCM

(KNCM)

This work extends the work of Al-Behadili et al.

(2015), who proposed a kernel-based distance met-

ric. We extend this idea towards semi-supervised

learning of non-linearly separable classes using a low-

dimensional kernel-based data representation. Recall-

ing the distance proposed by Mensink et al. (2013a)

d(x, µ

) =

W x −W

W µ

and setting

x = W

W x and

= W

W µ

, the distance becomes

d(x, µ

) =

x −

−

x +

. (10)

Applying the transformation to a higher-dimensional

space to

x and

, respectively, yields the kernel based

distance

kernel

(

) = K(

x) − K(

)

− K(

x) + K(

), (11)

which, in case of a Gaussian RBF, is given by

kernel

(x, µ

) = 2 − 2exp

−

W x −W

W µ

2σ

. (12)

Adopting the approach of Mensink et al. (2013a) we

obtain the posterior probability

p(c|x) =

exp



−

kernel

(x, µ

)



classes

∑

˜c=1

exp



−

kernel

(x, µ

˜c

)



(13)

and compute the matrix W

W by maximizing the log-

posterior of the correct prediction using gradient as-

cent.

4 DATASET

Since KNCM is proposed to work with non-linear

systems without losing the key features of NCMC,

i.e. the accuracy and the short processing time, we

apply it to a non-linearly separable gesture dataset.

We will evaluate and compare the recognition perfor-

mance of the KNCM approach with that of the the

NCMC method.

A Kinect sensor has been used by Fothergill et al.

(2012) to acquire a database of gestures which are

mainly performed with both hands simultaneously.

A database of emblematic gestures performed with

a single forearm and hand has been published by

Richarz and Fink (2011), where the 3D trajectories

were inferred from stereo image data. A dataset

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

284

of single-arm emblematic gestures acquired with a

Kinect sensor is described by Al-Behadili et al.

(2014)

. We use the dataset of Al-Behadili et al.

(2014), but since each gesture is repeated three times

in the published version, we performed a subdivision

of the dataset into single repetitions, resulting in 2878

gestures altogether. The ﬁrst six features are adopted

from Al-Behadili et al. (2014): three features for the

x, y and z coordinates of the mean vector, and three

features for the extension along the x, y and z axis.

The motion direction is transformed into the seventh

feature as follows:

• A principal component analysis of the dataset is

performed. A 3D trajectory is considered a two-

axes gesture if the projection on the eigenvec-

tor belonging to the second-largest eigenvalue is

larger than 60% of the projection on the eigen-

vector belonging to the largest eigenvalue. In this

case, the ﬁrst two principal components are kept

for the subsequent analysis. Otherwise, only the

ﬁrst principal component is kept as the gesture

then is a one-axis gesture.

• The signs of the selected principal components are

computed for each coordinate.

• A value of 1 (2) is assigned if more than 80% of

the coordinates are positive (negative). In the case

of no predominant direction, a value of 3 is as-

signed. Principal components not selected by the

described procedure are assigned a value of 0.

• The assigned direction values are concatenated in

the order of the principal components, forming a

base-4 number which is then transformed to a dec-

imal number denoting the direction information.

The total length of the normalized gesture is taken as

the last feature. We found this compact set of fea-

tures to be a favourable choice after having performed

many experiments with more extensive feature sets

proposed by e.g. Bhuyan et al. (2008) and Yoon et al.

(2001) including position, speed, direction, orienta-

tion, curvature, chain code etc.

5 EXPERIMENTS AND RESULTS

5.1 Experimental Setup

Since falsely assigned labels have a strong effect on

the performance of a semi-supervised learning algo-

rithm, we introduce a conﬁdence threshold and re-

ject possible outliers, i.e. samples exceeding a dis-

The complete dataset is available at http://www.bv.e-

technik.tu-dortmund.de

tance threshold. The labels of samples that do not

exceed the threshold are added to the training dataset

of the classiﬁer. The same approach is applied to the

KNCM and the NCMC classiﬁers, respectively. We

used the code of NCMC

as published by Mensink

et al. (2013a).

The threshold is based on an independent valida-

tion dataset. Consequently, the full dataset is subdi-

vided into four parts: a labelled initial training set, a

labelled validation set, an unlabelled learning set and

a labelled test set. At the beginning of the experi-

ment, the classiﬁers are adapted to the initial training

set and the conﬁdence threshold is computed based on

the validation set. The learning set is further subdi-

vided into so-called “buckets” that represent a stream

of data. The buckets are presented to the classiﬁers

one by one. The classiﬁers then assign labels to the

samples contained in the bucket, respectively, and add

the samples that do not exceed the training threshold

with the assigned labels to the training data. Then the

classiﬁers are adapted to the extended training set, and

a new conﬁdence threshold is computed. This process

is repeated until the last bucket has been presented

to the classiﬁers. After each training process of the

classiﬁers, we evaluate the accuracy of the classiﬁers

based on the test set. In addition to the accuracy, we

track the computation time required by each training

and prediction stage and the training set size. Addi-

tionally, we train a second version of each classiﬁer

with the correct labels to evaluate the performance of

a fully supervised learning scenario in each step.

The semi-supervised learning experiment is re-

peated for three different sizes of the initial training

set: 1%, 5% and 10% of the total dataset. In all exper-

iments, the test and the validation set comprise 20%

and 15% of the total dataset, respectively. The re-

mainder is the unlabelled learning set, which is sub-

divided into buckets of 100 samples each. The sets

are formed using a class-wise random partition, i.e.

1% of the training set corresponds to 1% of the sam-

ples from each class, respectively. Since each of the

nine gestures in the dataset is represented by a dif-

ferent amount of samples, the amount of samples in

the initial training set may be as low as two sam-

ples in the case of class nine and an initial training

set comprising 1% of the total data. Each experiment

is repeated for four different dimensions of the sub-

space h =

{

2, 4, 6, 8

}

, respectively, resulting in twelve

different experiments. Due to the random partition

of the data, the results of the experiments may de-

pend on how the initial training set has been selected.

To estimate the expected outcome of the experiment,

each experiment is repeated 100 times with a differ-

https://staff.fnwi.uva.nl/t.e.j.mensink/code.php

Non-linear Distance-based Semi-supervised Multi-class Gesture Recognition

285

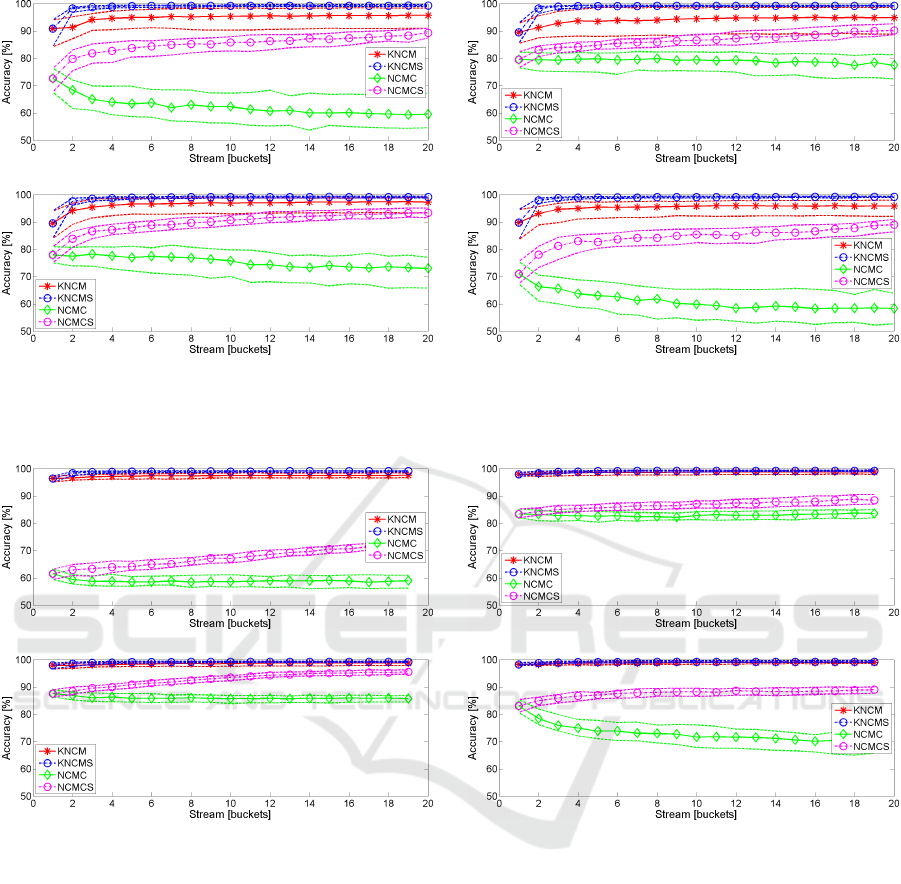
(a) (b)

Figure 2: Median prediction accuracy of the classiﬁers for an initial training set comprising 1% of the total data. KNCMS

and NCMCS denote the supervised version of the KNCM and NCMC, respectively. The dashed lines correspond to the 25%

and 75% quantiles and represent the spread over 100 repetitions. (a) h = 2. (b) h = 4. (c) h = 6. (d) h = 8.

(a) (b)

Figure 3: Median prediction accuracy of the classiﬁers for 5% of the total data used as initial training set. KNCMS and

NCMCS denote the supervised version of the KNCM and NCMC, respectively. The dashed lines correspond to the 25% and

75% quantiles and represent the spread over the 100 repetitions. (a) h = 2. (b) h = 4. (c) h = 6. (d) h = 8.

ent random permutation. Both classiﬁers use the same

random permutation for each experiment during these

100 repetitions.

The NCMC requires the speciﬁcation of the num-

ber of centroids per class N

centroids

. There is, however,

a function within the utilised code package published

by Mensink et al. (2013a) that computes the optimal

number of centroids per class. We apply this code to

specify the best N

centroids

for each projection matrix

dimension. The resulting values were N

centroids

= 2

for the four dimensions of the subspace, respectively.

In case of N

centroids

> N

, i.e. the number of class c

samples in the initial training is smaller than the num-

ber of centroids, we start by setting N

centroids

> N

and

then gradually increase N

centroids

until it equals the op-

timal value.

5.2 Results and Performances Study

Figs. 2–4 show the prediction accuracy of KNCM and

NCMC. Notably, the ﬁrst bucket corresponds to the

initial training set. The remaining results thus may

be directly compared to the result obtained by using

the initial training set. For large training sets (see Fig.

4), the accuracy of the KNCM equals the accuracy

of the supervised version. The high initial accuracy

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

286

(a) (b)

Figure 4: Median prediction accuracy of the classiﬁers for 10% of the total data used as initial training set. KNCMS and

NCMCS denote the supervised version of the KNCM and NCMC, respectively. The dashed lines correspond to the 25% and

75% quantiles and represent the spread over the 100 repetitions. (a) h = 2. (b) h = 4. (c) h = 6. (d) h = 8.

(a) (b)

Figure 5: Time consumed by the classiﬁers. (a) Initial training set: 1% of total data. (b) Initial training set: 5% of total

data. (c) Initial training set: 10% of total data. (d) Runtime (KNCM

and NCMC

) and samples in the training set (KNCM

and NCMC

) for the KNCM and the NCMC, respectively. The initial training set size is 1% of the total data, and the

dimensionality is h = 2.

is kept throughout the learning process. If the size

of the training set is reduced (see Fig. 2–3) the ac-

curacy of the semi-supervised KNCM does not reach

the optimal value of the fully supervised KNCM. It,

however, increases strongly over the ﬁrst few buck-

ets and approaches the fully supervised KNCM. The

difference between the semi-supervised KNCM and

the fully supervised KNCM increases with decreas-

ing dimensions of the projection subspace. However,

the effect of the subspace dimension on the KNCM

accuracy is rather subtle and thus it is possible to use

subspace projections of very low dimension.

The accuracy of the NCMC, in contrast, shows a

larger difference to its fully supervised counterpart if

the number of presented buckets increases. While the

fully supervised NCMC shows an increasing accuracy

in the course of the learning experiment, the accuracy

of the semi-supervised NCMC seems constant in the

best case and exhibits a strong decrease in some ex-

periments. Both the semi-supervised NCMC and the

fully supervised NCMC do not reach the accuracy of

the KNCM in all experiments. The decreasing accu-

racy of the NCMC suggests that the NCMC adds false

labels to the training set. This may be due to the low

initial prediction accuracy. The effect is less notice-

able if the size of the training set increases. Further-

Non-linear Distance-based Semi-supervised Multi-class Gesture Recognition

287

more, this effect seems to be strong for both the full

dimension of the data set and a very small subspace

dimension. The former may be related to the estima-

tion of many parameters while the latter may be due to

in insufﬁcient subspace dimension that does not allow

for a separation of the classes.

In addition to the gain in prediction accuracy, the

runtime of the KNCM is considerably lower than the

runtime of the NCMC, as shown in Fig. 5. The de-

creasing accuracy of the NCMC suggests that the

NCMC method results in the addition of more false

labels to the training set, possibly leading to a larger

total number of samples. However, the opposite is

true. Fig. 5(d) shows the median runtime and the me-

dian of the training set size for an initial training set

comprising 1% of the total data and a dimensionality

of h = 2. This exemplary semi-supervised learning

progress is similar to the other experiments. Fig. 5(d)

clearly shows that the runtime is independent of the

training set size.

6 CONCLUSION

The proposed KNCM shows an increased accuracy

and a lower runtime in comparison to the original

NCMC. The high accuracy is maintained for ex-

tremely small dimensional subspace projections. Fur-

thermore, the KNCM and its ability to reject outliers

has been demonstrated in a semi-supervised learning

scenario of gestures. The semi-supervised KNCM

achieves accuracies that are comparable to a fully su-

pervised learning scenario. Since the proposed algo-

rithm is not limited to gesture data, it is expected to be

applicable to any semi-supervised learning scenario.

REFERENCES

Al-Behadili, H., W

ohler, C., and Grumpe, A. (2014). Semi-

supervised learning of emblematic gestures. AT-

AUTOMATISIERUNGSTECHNIK, 62(10):732–739.

Al-Behadili, H., W

ohler, C., and Grumpe, A. (2015). Non-

Linear Distance Based Large Scale Data Classiﬁca-

tions. In 3’rd International conference on image In-

formation Processing (ICIIP), page In Press. IEEE.

Altman, N. S. (1992). An introduction to kernel and nearest-

neighbor nonparametric regression. The American

Statistician, 46(3):175–185.

Bhuyan, M., Bora, P., and Ghosh, D. (2008). Trajec-

tory guided recognition of hand gestures having only

global motions. International Journal of Computer

Science, Fall.

Boiman, O., Shechtman, E., and Irani, M. (2008). In de-

fense of nearest-neighbor based image classiﬁcation.

In Computer Vision and Pattern Recognition, 2008.

CVPR 2008. IEEE Conference on, pages 1–8. IEEE.

Cover, T. and Hart, P. (1967). Nearest neighbor pattern clas-

siﬁcation. Information Theory, IEEE Transactions on,

13(1):21–27.

Elmezain, M., Al-Hamadi, A., Rashid, O., and Michaelis,

B. (2009). Posture and Gesture Recognition for

Human-Computer Interaction. In Jayanthakumaran,

K., editor, Advanced Technologies, pages 415–440.

InTech, Rijeka, Croatia.

Fothergill, S., Mentis, H., Kohli, P., and Nowozin, S.

(2012). Instructing people for training gestural inter-

active systems. In Proceedings of the SIGCHI Confer-

ence on Human Factors in Computing Systems, pages

1737–1746. ACM.

Guillaumin, M., Mensink, T., Verbeek, J., and Schmid, C.

(2009). Tagprop: Discriminative metric learning in

nearest neighbor models for image auto-annotation. In

Computer Vision, 2009 IEEE 12th International Con-

ference on, pages 309–316. IEEE.

Kung, S. Y. (2014). Kernel Methods and Machine Learning.

Cambridge University Press.

Mensink, T., Verbeek, J., Perronnin, F., and Csurka, G.

(2013a). Distance-based image classiﬁcation: Gener-

alizing to new classes at near-zero cost. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

35(11):2624–2637.

Mensink, T., Verbeek, J., Perronnin, F., and Csurka, G.

(2013b). Large scale metric learning for distance-

based image classiﬁcation on open ended data sets. In

Advanced Topics in Computer Vision, pages 243–276.

Springer.

Richarz, J. and Fink, G. A. (2011). Visual recognition of

3d emblematic gestures in an hmm framework. Jour-

nal of Ambient Intelligence and Smart Environments,

3(3):193–211.

Schneider, P., Biehl, M., and Hammer, B. (2009). Adap-

tive relevance matrices in learning vector quantiza-

tion. Neural Computation, 21(12):3532–3561.

Theodoridis, S., Pikrakis, A., Koutroumbas, K., and

Cavouras, D. (2010). Introduction to Pattern Recog-

nition: A Matlab Approach. Academic Press.

Webb, A. R. (2003). Statistical pattern recognition. John

Wiley & Sons.

Yoon, H.-S., Soh, J., Bae, Y. J., and Yang, H. S. (2001).

Hand gesture recognition using combined features of

location, angle and velocity. Pattern recognition,

34(7):1491–1501.

Zhu, X. and Goldberg, A. B. (2009). Introduction to Semi-

supervised Learning. Synthesis lectures on artiﬁcial

intelligence and machine learning. Morgan & Clay-

pool Publishers.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

288