Neural Network based Novelty Detection for Incremental

Semi-supervised Learning in Multi-class Gesture Recognition

Husam Al-Behadili

1,2

, Arne Grumpe

and Christian W

ohler

Electrical Engineering, University of Mustansiriyah, Al-Mustansiriyah, Box 46007, Baghdad, Iraq

Image Analysis Group, TU Dortmund University, Otto-Hahn-Str. 4, D–44227, Dortmund, Germany

Keywords:

Data Stream, Neural Network, Extreme learning Machine (ELM), Novelty Detection, Incremental Learning,

Semi-supervised Learning, Extreme Value Theory (EVT), Conﬁdence Band.

Abstract:

The problems of inﬁnitely long data streams and its concept drift as well as non-linearly separable classes

and the possible emergence of “novel classes” are topics of high relevance for gesture data streaming based

automatic recognition systems. To address these problems we apply a semi-supervised learning technique

using a neural network in combination with an incremental update rule. Neural networks have been shown

to handle non-linearly separable data and the incremental update ensures that the parameters of the classiﬁer

follow the “concept-drift” without the necessity of an increased training set. Since a semi-supervised learning

technique is sensitive to false labels, we apply an outlier detection method based on extreme value theory and

conﬁdence band intervals. The proposed algorithm uses the extreme learning machine, which is easily updated

and works with multi-classes. A comparison with an auto-encoder neural network shows that the proposed

algorithm has superior properties. Especially, the processing time is greatly reduced.

1 INTRODUCTION

When people start a conversation, they commonly use

hand motions. These motions of the hand may also

be used to communicate with machines in Human-

Machine Interaction (HMI). In this context, they are

called “gestures”. Since gestures are considered an

intuitive, fast and save way in HMI, they are included

in many applications ranging from computer games to

applications in the medical industry (e.g. Yusoff et al.

(2013)). Gestures of the same class, however, may

be performed in a different manner by different per-

sons or by the same individual if she/he performs the

gesture more than once. Hence, the classiﬁer should

be trained with all possible gestures to get an accept-

able recognition rate. Unfortunately, manually la-

belled data are scarce. Unlabelled data, in contrast,

may be streamed continuously. Consequently, semi-

supervised learning may be applied to solve this prob-

lem. Semi-supervised learning corresponds to ﬁrst

training a classiﬁer on a labelled data set in a super-

vised manner and updating the training set using the

labels assigned by the classiﬁer itself (Zhu and Gold-

berg, 2009). However, the problems arising from the

usage of streamed data are the “inﬁnite length” and

the “concept-drift”. They were addressed by most of

the existing on-line algorithms (Masud et al., 2011).

In addition, non-linearly separable distributions of the

data, the emersion of new classes or outliers, and the

computational complexity are possible problems. To

address these problems we apply a semi-supervised

learning technique using a neural network in combi-

nation with an incremental update rule. Neural net-

works have been shown to handle non-linearly sep-

arable data and the incremental update ensures that

the parameters of the classiﬁer follow the “concept-

drift” without the necessity of an increased training

set. Since a semi-supervised learning technique is

sensitive to false labels, we apply an outlier detec-

tion method based on the concepts of extreme value

theory and conﬁdence bands interval to suppress false

labels that will potentially affect the performance of

the classiﬁer after the next training cycle.

2 RELATED WORK

There have been several research studies on semi-

supervised learning (Zhu and Goldberg, 2009). The

semi-supervised techniques are categorized in three

main types, which are: First, guessing the unlabelled

data and subsequently retraining the classiﬁer using

Al-Behadili, H., Grumpe, A. and Wöhler, C.

Neural Network based Novelty Detection for Incremental Semi-supervised Learning in Multi-class Gesture Recognition.

DOI: 10.5220/0005674202870294

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 289-296

ISBN: 978-989-758-175-5

289

these labels, e.g. EM, co-training, and transductive

SVM (Zhu and Goldberg, 2009). Second, ﬁnding

additional features derived from the unlabelled data

(Johnson and Zhang, 2015). Third, manifold reg-

ularization has been used to leverage the labelled

and unlabelled data (Huang et al., 2014). Recently,

the extreme learning machine was applied to semi-

supervised learning, since it has favourable features.

Huang et al. (2014) constructed the Laplacian graph

from labelled and unlabelled data to extend the ex-

treme learning machine for semi-supervised learning.

They, however, supposed all unlabelled data to be

available together at the beginning of the training.

Hence, it is not suitable for data streams. A new ap-

proach by Li et al. (2013) applied co-training to train

the ELM in a semi-supervised manner. Since, this al-

gorithm repeatedly trains several ELMs, it is consid-

ered computationally costly. Since neural networks

have the ability to approximate the non-linear map-

ping from features to classes directly from the input

samples, several researchers proposed different algo-

rithms of incremental neural networks. Huang et al.

(2006a) introduced the “incremental extreme learn-

ing machine” (IELM) by adding randomly generated

nodes to a single-layer feed-forward network (SLFN)

and computed the output weight analytically for the

new nodes only. Since semi-supervised learning is

sensitive to false labels, the proposed algorithm needs

to detect and reject the outliers which may affect on

the performance of the algorithm. Pimentel et al.

(2014) describe methods solving the novelty detec-

tion problem by using statistical techniques or neu-

ral networks. Applications of neural networks have

been implemented in many domains (Hugueny et al.,

2009). Due to the large variety of artiﬁcial neural

networks many different neural network approaches

may be used for novelty detection. Tax (2001) used

the auto-associative neural networks (AANN) as an

one class classiﬁers within the data discretion, out-

lier and novelty detection toolbox (ddtools)

(Tax,

2015), where the auto-encoder function is called “au-

toenc dd”. It is a reference for our work and is ex-

plained in detail in the next section.

3 REFERENCE METHODS

3.1 Extreme Learning Machine (ELM)

The concept of the ELM is described in detail by

Huang et al. (2006b), whose description we follow

here. According to their approach, for a SLFN with L

http://prlab.tudelft.nl/david-tax/dd tools.html

hidden neurons the output is given by

(~x

) =

∑

i=1

G(~a

,~x

) ~x

∈ R

,~a

∈ R

(1)

with β

as the output weight, ~a

and b

as the learn-

ing parameters, G(~a

,~x

) as hidden neuron output i,

and ~x

as the feature vector associated with training

sample j. It is

G(~a

,~x

) = g(~a

·~x

+ b

), b

∈ R (2)

with ~a

and b

as the ith neuron’s input weight vector

and bias. For hidden neurons with radial basis func-

tion (RBF) characteristic it is,

G(~a

,~x

) = g(b



−~a



) b

∈ R

(3)

with~a

and b

as the centre and width of RBF neuron i.

refers to all positive real numbers (Huang et al.,

2006b).

The ELM is a SLFN network, and the equations

above apply to it. Following Huang et al. (2006b),

suppose we have m arbitrary distinct sample (~x

∈ R

) consisting of a feature vector ~x

and a tar-

get vector

containing one value for each of the c

classes, respectively. Notably, it is

= +1 for the

output neuron belonging to the class of the sample

and

= −1 for the other output neurons, respectively.

The ELM has L neurons. An error-free approximation

of the m samples by this ELM then implies the exis-

tence of a set of parameters β

, ~a

and b

fulﬁlling

(~x

) = t

, j = 1 · · · m, (4)

which can be written as a matrix

H · β

β = T

T (5)

H =







G(~a

,~x

) ··· G(~a

,~x

)

G(~a

,~x

) ··· G(~a

,~x

)







m×L

(6)

β =













L×c

and T

T =













m×c

(7)

where

denotes the vector containing the ith neu-

ron’s output weight for all classes and the mtrix H

denotes the hidden layer output. According to Huang

et al. (2006b), the procedure of training the ELM is as

follows:

• The ﬁrst step is to assign the input parameters (i.e.

, and b

, i = 1, . . . , L) randomly.

• Analytical computation of the matrix H

H is per-

formed according to Eq. (7).

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

290

• The output weights are then estimated using (5).

As shown by Huang et al. (2006b), the problem here

is to minimize the error in (5), i.e.

H · β

β − T

. Since

(5) is a linear system in the output weights, the output

weights are estimated by Huang et al. (2006b) using

the pseudoinverse of the output matrix of the hidden

layer according to H

†

= (H

−1

(Rao and Mi-

tra, 1971):

β = H

†

· T

T (8)

As suggested by Huang et al. (2006b), the singular

value decomposition (SVD) (Rao and Mitra, 1971) is

used to compute the pseudoinverse H

†

. The labels of

the new samples can then be obtained by using the

estimates

β and H

†

in (7).

3.2 Extreme Value Theory (EVT)

The conventional approaches of the novelty detec-

tion mostly require one threshold or a set of class-

wise thresholds computed by additional manually la-

belled data or by using the cross-validation process,

which are either need additional labelled data or are

time consuming. In contrast, the extreme value the-

ory (EVT) as described by Roberts (1999) and Clifton

et al. (2008) avoids these problems. It is a statistical

theory used to model the extreme values, i.e. maxima

or minima in the one-dimensional case, in the tails of

the distributions. Following Roberts (1999), let there

be a set of m i.i.d. random samples X =

{

,~x

...,~x

}

each of them is n-dimensional and distributed as given

by the probability density function f (~x). Further-

more, let the extreme value of X be ~x

max

. Given the

set X , the probability of ~x being more extreme than

max

is the extreme value probability which expressed

as P

(~x|X ) = P(~x

<~x). There are three types of dis-

tributions of the EVD as stated by the Fisher-Tippett

theorem (Fisher and Tippett, 1928): the Gumbel dis-

tribution, the Frechet distribution and the Weibull dis-

tribution (Roberts, 1999). As described by Roberts

(1999) and Clifton et al. (2008), the Gumbel distri-

bution models the EVD of data originating from the

one-dimensional one-sided normal distribution with

a mean value of zero and a variance of 1, i.e. D =



N (0, 1)



. According to Clifton et al. (2008), the

Gumbel distribution for a one-dimensional variable x

Gumbel

(x|X ) = exp



−exp



−

x − µ



, (9)

is deﬁned by the location parameter

= (2 ln(m))

0.5

−

ln(ln(m)) + ln(2π)

2(2ln(m))

0.5

(10)

and the scale parameter

= (2 ln(m))

0.5

. (11)

Both parameters depend only on m, i.e. the number

of samples drawn from D. These minimize or absorb

the effect of the amount of training data on the ﬁnal

results and thus the threshold remains unchanged with

an increasing amount training data.

We deﬁne a threshold P

that is based on the ex-

treme values of the known classes. A novelty is de-

tected if P

exceeds this threshold. As may be ver-

iﬁed from the equations above, the threshold in EVT

has a direct statistical interpretation and does not de-

pend on the distribution of the classes whereas the

conventional thresholds depend on the distribution of

the classes.

3.3 Auto-associative Neural Networks

Auto-associative neural networks (AANN) or auto-

encoder networks (AutoENC), as they are called by

Tax (2001), are neural networks that learn a data rep-

resentation (Hertz et al., 1991), i.e. an AANN recon-

structs the input pattern at their output layer. In this

work, we apply the auto-encoder from the toolbox

presented by Tax and Duin (1999). In this toolbox the

auto-encoder architecture has only one hidden layer

with h

auto

hidden units. Sigmoid transfer functions

are used for the hidden neurons. It is trained by min-

imizing the mean squared deviation of the input from

the output. The error is used as a measure for the nov-

elty detection. It is supposed that the target patterns

will be reconstructed with smaller errors than outliers.

The error E

AANN

of an input ~x is

AANN

(~x,~w) −~x

(12)

where f

ANN

is transfer function of the AANN and ~w

is a vector containing its parameters. The problems of

the AANN to novelty detection are the same problems

as those arising from the conventional application of

neural networks to classiﬁcation problems: It requires

a pre-deﬁned number of neurons, a learning rate, and

stopping criteria from an expert user. In our experi-

ments, the best number of neurons is 5, which is the

default number in the function of the toolbox. We also

used the default outlier percentage 5% that is used to

compute the threshold of the novelty.

3.4 Conﬁdence Bands

Since measurements are affected by noise, models

derived from these measurements differ for each ac-

quired set of new data. The conﬁdence band en-

closes all models obtained from the measurements

with a speciﬁed probability (Kardaun, 2005). Con-

ﬁdence bands are computed in several approaches

Neural Network based Novelty Detection for Incremental Semi-supervised Learning in Multi-class Gesture Recognition

291

(e.g. Kendall et al., 2007). In the context of semi-

supervised learning, the conﬁdence bands of a poly-

nomial classiﬁer are used by Al-Behadili et al. (2014)

to detect outlier samples.

4 THE PROPOSED ALGORITHM

Here, we propose a method to update the ELM in-

crementally and to apply the outliers detection using

the EVT and the conﬁdence band to the output of the

ELM to reject the outliers. The proposed algorithm

extends the approach of Al-Behadili et al. (2015),

which uses only EVT for detecting the outliers. It

consists of two phases.

4.1 Incremental Learning Phase

The incremental updating rule is derived based on the

pseudoinverse method introduced by Lan et al. (2009)

according to

M = H

H and P

P = H

T . (13)

Hence, β

β = M

−1

P. (14)

The dimension of M

M is L × L and the dimension of

the P

P is L × c, where L corresponds to the number of

hidden neurons and c to the number of classes.

Suppose that we have m

(0)

labelled samples for

initial training. We then compute M

(0)

= H

(0)

and P

(0)

= H

(0)

according to (13). Hence, β

(0)

−1

(0)

Incremental learning is achieved by adding

chunks of samples to the training set. If the number

of samples

ˆx in the chunk k + 1 is ˆm then the hidden

layer output matrix

H corresponding to the new chunk

of data is

H =







G(~a

ˆx

) ··· G(~a

ˆx

)

G(~a

ˆx

ˆm

) ··· G(~a

ˆx

ˆm

)







ˆm×L

(15)

From (15) and (13) it follows that

M =

H and

P =

T corresponding to the new chunk data. Then

(k+1)

= M

(k)

M and P

(k+1)

= P

(k)

P (16)

Finally, using (14) the updated output is β

(k+1)

−1

(k+1)

4.2 Novelty Detection Phase

4.2.1 Novelty Detection using EVT

According to Huang et al. (2006b), the output of the

ELM is around +1 for the class that the sample be-

longs to it and around −1 for the other classes. This

follows immediately from the target values used for

the training of the ELM. If the output of the winner

class is exactly +1 then this result is similar to the

training data and thus highly believable. The conﬁ-

dence of the result decreases with an increasing dis-

tance of the winner output class from the ideal value

of +1. Furthermore, the linear least squares optimiza-

tion applied in the training yields mean-free normally

distributed residuals. Consequently, the absolute dif-

ference between the ELM output and the ideal value,

i.e. a vector that contains +1 at the position of the

winning neuron and −1 at all other positions, will

originate from a mean free one-sided normal distribu-

tion. Additionally, we divide the absolute difference

by the standard deviation of the residuals, i.e. the sum

of the squared residuals, to arrive at a N (0,1) distri-

bution.

Recalling (5) and substituting (8), we arrive at the

prediction D

D of the training set

D = H

H(H

−1

T . (17)

Notably, each column of D

D contains the predicted val-

ues for one class. Let

and

be the vector contain-

ing the predicted values and the target values of class

c, respectively. The sum of the squared residuals is

then given by

−

(18)

H(H

−1

. (19)

Notably, H

H = M

M and H

is the cth column of P

Consequently, the ﬁrst summand on the right side of

(19) may be incremented using (16). The term

the sum of the squared target values. Consequently, it

may be incremented by adding the squared target val-

ues of additional samples. Dividing r

by the number

of samples and taking the square root results in the

standard deviation of the residuals. Notably, this ap-

proach yields a class-wise standard deviation which

represents the different models formed by the output

layer of the ELM.

After division by the class-wise standard devia-

tion, the absolute difference of the ELM output and

the ideal value originates from a one-sided normal

distribution and is thus modelled by the Gumbel dis-

tribution of the extreme value theory (Clifton et al.,

2008). Accordingly, the highly believable samples

have P

= 0 and the ideal novel sample yields P

= 1.

Thus we set P

= 0.9 and ﬂag a sample to be novel if

at least two output neurons detect a novelty.

To ensure only trusted labels in the new training

set, we apply additional conditions. If at least one out-

put neuron detects a novelty, we do not consider the

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

292

label trustworthy and do not add it to the training set.

Furthermore, since in the ideal case the winner class

output value should be +1 and all other neurons out-

put −1 and the difference between the winning neu-

ron and the second largest output value is supposed

to be 2. We have noticed that the ELM outputs two

positive values in case of unseen classes, resulting

in a difference less than 1. Therefore, the newly la-

belled samples should fulﬁll another condition to be

accepted in the next training phase: The difference be-

tween the ﬁrst and second largest output values should

exceed speciﬁc threshold. Here, we set the threshold

to 1.

4.2.2 Novelty Detection using Conﬁdence Bands

Equation (5) is a system of linear equations for the

output weights, i.e. the output of the ELM is a

weighted linear combination of the hidden layer acti-

vations, where the weights represent the parameters of

a linear model (Huang et al., 2006b). The conﬁdence

band intervals of the output decision can thus be esti-

mated. Based on the general derivation of the conﬁ-

dence bands of a linear multivariate regression func-

tion given by Kardaun (2005), the conﬁdence band

η(~q) of the neural network output ~q for a test sample

~x can be estimated according to

η(~q) = t

v,α

−1

/v, (20)

where r

= d(~x

) − t(~x

) is the residual of sample i,

v = m − N

is the number of degrees of freedom, with

as the number of free parameters of the model,

v,α

is the critical value of the t-distribution which de-

pends on v and the probability threshold α. A similar

expression is obtained by Al-Behadili et al. (2014) for

the conﬁdence band of a polynomial classiﬁer, where

the mathematical framework described by Kardaun

(2005) is used as well. Here, the number of free pa-

rameters N

is equal to the hidden neuron number.

Since H

H = M

M and the residuals r

= d(~x

) − t(~x

)

appear in the squared sum, we apply Eq. (16) and Eq.

(19) to incrementally update the conﬁdence bands.

The standard value 0.05 of α is used.

The sample ~x is taken to be novel if the inequality

(~x) − d

(~x) < z · [η

(~x) + η

(~x)] (21)

is fulﬁlled, where d

(~x) and d

(~x) are the largest and

second largest decision values of the classiﬁer of the

sample ~x, η

(~x) and η

(~x) the corresponding conﬁ-

dence band widths and z is a given constant (here

z = 75). The condition (21) has been proposed by Sa-

kic (2012), who used it for the identiﬁcation of unre-

liable sample labels in the context of semi-supervised

learning.

Finally, the sample~x has been considered as novel

if both conditions P

≥ P

and Eq. (21), which corre-

spond to the EVT and conﬁdence band, respectively,

indicate it as novel.

5 GESTURE DATA SET

The database by Richarz and Fink (2011) comprises

emblematic gestures of single-hand gestures acquired

by a pair of asynchronous stereo cameras used to

compute the 3D trajectories. A data set which com-

prises 3D trajectories performed with a single hand

acquired by a Kinect sensor is described by Al-

Behadili et al. (2014). Using that data set

, we seg-

ment the original three repetitions per gesture into

single repetitions, yielding a total number of 2878

gestures. In addition, we adopt six features from Al-

Behadili et al. (2014): the mean and extent in x, y and

z direction, respectively. The remaining two features

are modiﬁed. The seventh feature is a code which is

extracted from the direction of movement:

• The principal components of the 3D trajectory are

computed and analysed. Let λ

and λ

be the

largest and the second largest eigenvalues of the

covariance matrix of the 3D coordinates, respec-

tively. If λ

> 0.6 λ

the gesture is considered a

two-axis gesture. Otherwise the gesture is con-

sidered a one axis gesture. In the former case we

keep the ﬁrst two principal components and in the

latter case we keep only the ﬁrst principal compo-

nent for the remaining analysis.

• The 3D coordinates are projected onto the se-

lected principal components and the sign of the

velocity of each projected coordinate is computed.

• Based on the amount of positive and negative val-

ues, we assign the following value to each princi-

pal component, respectively. We assign a value of

1 or 2 if more than 80% of the coordinates are pos-

itive or negative, respectively. Otherwise, the ges-

ture has no predominant direction and is assigned

a value of 3. Furthermore, a value of 0 is assigned

to principal components that were not selected in

the ﬁrst step.

• The three direction values are then interpreted as

a base-4 number, and the corresponding decimal

representation is computed to combine all direc-

tions in one numerical value.

Finally, the last feature represents the total length of

the normalised gesture. This feature set has been cho-

The complete data set is available at http://www.bv.e-

technik.tu-dortmund.de

Neural Network based Novelty Detection for Incremental Semi-supervised Learning in Multi-class Gesture Recognition

293

sen after many experiments with other, more exten-

sive feature sets. Furthermore, a compact feature set

is desirable in the context of online learning.

6 EXPERIMENTAL SET-UP

The normal ELM neural network has been proven to

be a fast neural network (Huang et al., 2006b). More-

over, the incremental ELM is faster than normal ELM.

Hence, the main comparison will focus on the ac-

curacy rather than the time of processing. To show

the additional features of the proposed algorithm we

compare its results with the auto-encoder neural net-

work in the PRToolbox

(Tax and Duin, 1999). Sim-

ilar to our algorithm, this auto-encoder algorithm has

the ability to detect outliers. Hence, we used it in

the semi-supervised process to compare the two al-

gorithms.

The 2878 samples of the nine classes are ran-

domly divided into three disjoint data sets with frac-

tions 40%, 40%, and 20% for the training, the learn-

ing and the test set, respectively. The training set con-

tains all nine classes and each class is divided sepa-

rately, i.e. the training set contains 40% of the samples

of all classes. The novel class is then introduced by

excluding one class from the initial training set. The

learning set is split into chunks, so-called “buckets”,

of 100 samples.

Both classiﬁers are trained on the initial training

set. Then the accuracy and other measures are evalu-

ated based on the test set. Since the learning set emu-

lates the data stream, it is presented to the classiﬁer in

buckets, i.e. subsequent chunks of data. The buckets

are labelled by each classiﬁer. The data in the bucket,

which is considered an “outlier” or not believable, is

then removed and the classiﬁers are updated based on

the remaining data, i.e. we modify the training set by

adding the remaining samples, and update both classi-

ﬁers. The process is then repeated for the next bucket

of samples. Since the auto-encoder algorithm is not

incremental, the algorithm is retrained using the mod-

iﬁed training set while we use the proposed incremen-

tal update rule for the ELM. The procedure is repeated

until all buckets have been presented to the classiﬁers.

The modiﬁcation of the training set is done in two

steps. First, the sample is tested for novelty and then

the sample is tested for trusted predictions. We intro-

duce two ﬂags for the requirements to the proposed

ELM algorithm. New samples are considered novel if

the ﬁrst ﬂag set, i.e. the EVT output exceed the thresh-

old of 0.9. The selection of the samples which are in-

PRTool is available at http://prtools.org/software/

cluded into the training set is controlled by the second

ﬂag. This second ﬂag is set if the difference between

the winner class and the second class exceeds 1.

The auto-encoder labels the new sample with the

winner class label or as an “outlier”. Originally, the

auto-encoder is an one-class classiﬁer. However, us-

ing the function “multic” in the toolbox by Tax (2015)

allows for the classiﬁcation of multiple classes. This

is achieved by training one classiﬁer for each class.

Each classiﬁer outputs a real number between 0 and

1 similar to a probability. If this number is less than

a predeﬁned threshold, which was set by selecting the

ratio of the outliers in the training set to be 5%, it in-

dicates the new sample as an “outlier”. Otherwise,

the new sample is labelled as “target”. The “multic”

function labels the new sample as “outlier” if it does

not match any class, i.e. if it is indicated as “outlier”

by all classiﬁers, and it labels the new sample with the

most probable class, i.e. the maximum output class, if

more than one class is labelled as “target”.

Due to the different novelty detection approaches,

each algorithm will indicate different outliers. Fur-

thermore, the classiﬁers may assign different labels to

each sample. Consequently, the classiﬁcation prob-

lem solved by each classiﬁer may change after each

bucket of samples from the data stream has been anal-

ysed. It is thus possible that the training sets of the

different classiﬁers diverge, i.e. contain different sam-

ples and possibly false labels. The corresponding

changes in the classiﬁer architecture also have a se-

vere inﬂuence on the run time. The whole procedure

is thus repeated for 100 random subdivisions of the

data per class, i.e. each class is omitted from the train-

ing set once. We enforce identical random permuta-

tions for both classiﬁers, respectively, during each of

the 100 runs.

In addition to the accuracy, we track some nov-

elty detection metrics and the time required for the

update/retrain. We used the metric proposed by Ma-

sud et al. (2011) to evaluate both algorithms with re-

spect to their rates of novelty detection and classiﬁca-

tion errors. The novelty detection metrics are M

new

, and E

total

, which represent the fraction of novel

class samples that are incorrectly classiﬁed as existing

classes, the fraction of samples belonging to existing

classes that are mistaken as belonging to a novel class,

and the total misclassiﬁcation rate. Following Masud

et al. (2011), these metrics can be computed using

new

= F

· 100 (22)

new

= F

/(N − N

) · 100 (23)

total

= (F

+ F

)/N · 100 (24)

The results of the individual runs are available at

http://www.bv.e-technik.tu-dortmund.de

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

294

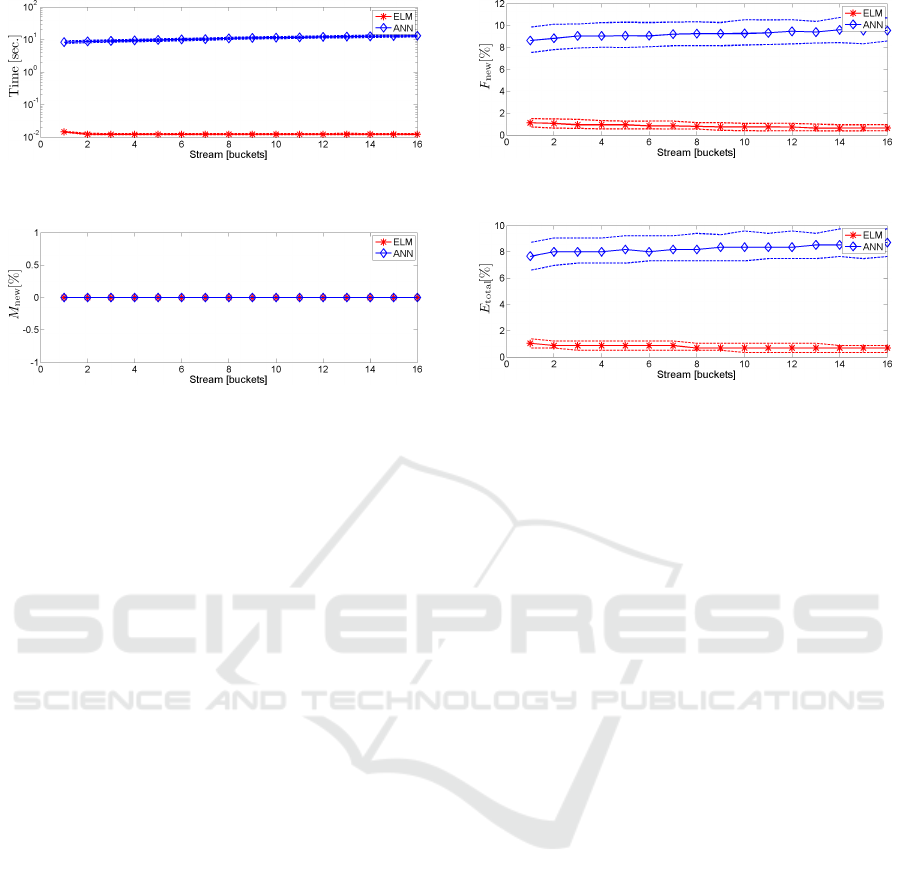
Figure 1: The time required for each bucket, i.e. classiﬁca-

tion and retraining of both classiﬁers.

Figure 2: The rate of missed novelties for the incremental

ELM and the AANN, respectively.

is the number of novel class samples that the clas-

siﬁer fails to detect and falsely labels them as existing

classes. It corresponds to the number of false nega-

tives for one class classiﬁers. N

represents the num-

ber of samples which belong to the novel class within

the presented samples. F

is the number of existing

class samples which are wrongly indicated as outliers

by the classiﬁer. It corresponds to the number of false

positives for one class classiﬁers. The total number of

samples presented to the classiﬁer is denoted by N. F

is the number of existing class samples that are mis-

classiﬁed as other existing classes. As seen from (24),

it is not necessary that E

total

corresponds to the sum of

new

and F

new

(Masud et al., 2011).

7 RESULTS

The run time of the classiﬁer matches the expectations

(Fig. 1). Since the proposed algorithm is incremental,

it requires less time to adapt. In any case the process-

ing time of the incremental ELM is of the order of

some milliseconds which helps to apply it to online

data streams.

Fig. 2 shows that the values M

new

of both algo-

rithms are zero, i.e. no outlier or novelty has been

missed. This is important since the outliers are sup-

posed to be near the boundary of the sample distri-

butions of all classes and thus accepting them would

signiﬁcantly affect the performance of the classiﬁers

in the next iterations. Fig. 3 shows the value of

new

, which is initially below 2 % for the proposed

algorithm whereas it starts at more than 8 % for the

AANN. The rate of false detections by the incremen-

Figure 3: The rate of falsely detected novelties for the in-

cremental ELM and the AANN, respectively.

Figure 4: The total error rate for the incremental ELM and

the AANN, respectively.

tal ELM decreases with an increasing amount of train-

ing data, reaching a ﬁnal level of less than 1 %. In

the case of the AANN, F

new

is increasing to more

than 9%. Although this means that a small fraction

of about 1–2 % of the samples belonging to known

classes is supposed to be outliers and, consequently,

they are rejected, this is not critical. In fact, this

removes the 1–2 % most extreme samples from the

semi-supervised training set and thus prevents possi-

bly false labels or sloppily performed gestures from

entering the training set. This leads to a slow gradual

adaptation of the learned sample distributions, lead-

ing to a ﬁnal stabilised value reﬂected by E

total

(Fig.

4). This behaviour is favourable in slowly concept-

drifting data streams where the sample distributions

change slowly over time. The auto-encoder, in con-

trast, rejects more samples, which leads to a very slow

adaptation. The effect of this novelty detection step is

directly apparent in the total error E

total

of both clas-

siﬁers. Initially, the error of the proposed approach

is around 1 % and decreases to less than 1 %. On

the other side, the total error of the auto-encoder is

initially around 8 % and increases with an increasing

new

8 SUMMARY AND CONCLUSION

We have presented an incremental neural network in

a semi-supervised learning scenario. In particular, we

have applied it to data streaming of emblematic arm

gestures, where it is possible that new classes appear

based on the continuously streamed data. This re-

laxes the need for a large and costly manually labelled

Neural Network based Novelty Detection for Incremental Semi-supervised Learning in Multi-class Gesture Recognition

295

data set. Using EVT, the algorithm uses a class-wise

statistical threshold for the rejection of outliers. It

thus does not require additional labelled data to de-

rive thresholds. More important, it works with mul-

tiple classes, and the normalisation prior to the EVT

ensures a class-wise threshold. Additionally, it is able

to separate the linearly unseparable gesture data. Im-

provements in the accuracy and processing time are

expected when applying this method to other types of

data. It might also be helpful for online fault detection

in industrial production processes.

REFERENCES

Al-Behadili, H., W

ohler, C., and Grumpe, A. (2014).

Semi-supervised learning of emblematic gestures. At-

Automatisierungstechnik, 62(10):732–739.

Al-Behadili, H., W

ohler, C., and Grumpe, A. (2015). Ex-

treme learning machine based novelty detection for

incremental semi-supervised learning. In 3’rd Inter-

national conference on image Information Processing

(ICIIP), page In Press. IEEE.

Clifton, D. A., Clifton, L. A., Bannister, P. R., and

Tarassenko, L. (2008). Automated novelty detec-

tion in industrial systems. In Advances of Computa-

tional Intelligence in Industrial Systems, pages 269–

296. Springer.

Fisher, R. A. and Tippett, L. H. C. (1928). Limiting forms

of the frequency distribution of the largest or smallest

member of a sample. In Mathematical Proceedings

of the Cambridge Philosophical Society, volume 24,

pages 180–190. Cambridge Univ Press.

Hertz, J., Krogh, A., and Palmer, R. G. (1991). Introduction

to the theory of neural computation, volume 1. Basic

Books.

Huang, G., Song, S., Gupta, J., and Wu, C. (2014).

Semi-supervised and unsupervised extreme learn-

ing machines. IEEE Transactions on Cybernetics,

44(12):2405–2417.

Huang, G.-B., Chen, L., and Siew, C.-K. (2006a). Universal

approximation using incremental constructive feed-

forward networks with random hidden nodes. IEEE

Transactions on Neural Networks, 17(4):879–892.

Huang, G.-B., Zhu, Q.-Y., and Siew, C.-K. (2006b). Ex-

treme learning machine: theory and applications.

Neurocomputing, 70(1):489–501.

Hugueny, S., Clifton, D. A., and Tarassenko, L. (2009).

Novelty detection with multivariate extreme value the-

ory, part ii: An analytical approach to unimodal esti-

mation. In Proc. MLSP, pages 1–6. IEEE.

Johnson, R. and Zhang, T. (2015). Semi-supervised learn-

ing with multi-view embedding: Theory and applica-

tion with convolutional neural networks. Proc. CoRR.

Kardaun, O. J. (2005). Classical methods of statistics: with

applications in fusion-oriented plasma physics, vol-

ume 1. Springer Science & Business Media.

Kendall, W. S., Marin, J.-M., and Robert, C. P. (2007). Con-

ﬁdence bands for brownian motion and applications

to monte carlo simulation. Statistics and Computing,

17(1):1–10.

Lan, Y., Soh, Y. C., and Huang, G.-B. (2009). Ensemble of

online sequential extreme learning machine. Neuro-

computing, 72(13):3391–3395.

Li, K., Zhang, J., Xu, H., Luo, S., and Li, H. (2013). A semi-

supervised extreme learning machine method based

on co-training. Journal of Computational Information

Systems, 9(1):207–214.

Masud, M. M., Gao, J., Khan, L., Han, J., and Thuraising-

ham, B. (2011). Classiﬁcation and novel class detec-

tion in concept-drifting data streams under time con-

straints. IEEE Transactions on Knowledge and Data

Engineering, 23(6):859–874.

Pimentel, M., Clifton, D., Clifton, L., and Tarassenko, L.

(2014). A review of novelty detection. Signal Pro-

cessing, 99:215–249.

Rao, C. R. and Mitra, S. K. (1971). Generalized inverse of

matrices and its applications, volume 7. Wiley New

York.

Richarz, J. and Fink, G. A. (2011). Visual recognition of

3d emblematic gestures in an hmm framework. Jour-

nal of Ambient Intelligence and Smart Environments,

3(3):193–211.

Roberts, S. J. (1999). Novelty detection using extreme value

statistics. IEE Proceedings-Vision, Image and Signal

Processing, 146(3):124–129.

Sakic, D. (2012). Semi-supervised learning using ensemble

methods gestures recognition. Master’s thesis, Uni-

versity of Dortmund.

Tax, D. (2001). One-class classiﬁcation: concept-learning

in the absence of counter-examples. PhD thesis, TU

Delft, Delft University of Technology.

Tax, D. (2015). Ddtools, the data description toolbox for

matlab.

Tax, D. M. J. and Duin, R. P. W. (1999). Support vector do-

main description. Pattern Recognition Letters, 20(11-

13):1191–1199.

Yusoff, Y. A., Basori, A. H., and Mohamed, F. (2013). In-

teractive hand and arm gesture control for 2d med-

ical image and 3d volumetric medical visualization.

Procedia-Social and Behavioral Sciences, 97:723–

729.

Zhu, X. and Goldberg, A. B. (2009). Introduction to semi-

supervised learning. Synthesis lectures on artiﬁcial

intelligence and machine learning, 3(1):1–130.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

296