Novel Ways to Estimate Homography from Local Afﬁne Transformations

Daniel Barath and Levente Hajder

MTA SZTAKI, Distributed Event Analysis Research Laboratory, Budapest, Hungary

Keywords:

Homography Estimation, Afﬁne Transformation, Perspective-invariance, Stereo Vision, Epipolar Geometry,

Planar Reconstruction.

Abstract:

State-of-the-art 3D reconstruction methods usually apply point correspondences in order to compute the 3D

geometry of objects represented by dense point clouds. However, objects with relatively large and ﬂat surfaces

can be most accurately reconstructed if the homographies between the corresponding patches are known. Here

we show how the homography between patches on a stereo image pair can be estimated. We discuss that these

proposed estimators are more accurate than the widely used point correspondence-based techniques because

the latter ones only consider the last column (the translation) of the afﬁne transformations, whereas the new

algorithms use all the afﬁne parameters. Moreover, we prove that afﬁne-invariance is equivalent to perspective-

invariance in the case of known epipolar geometry. Three homography estimators are proposed. The ﬁrst

one calculates the homography if at least two point correspondences and the related afﬁne transformations

are known. The second one computes the homography from only one point pair, if the epipolar geometry is

estimated beforehand. These methods are solved by linearization of the original equations, and the reﬁnements

can be carried out by numerical optimization. Finally, a hybrid homography estimator is proposed that uses

both point correspondences and photo-consistency between the patches. The presented methods have been

quantitatively validated on synthesized tests. We also show that the proposed methods are applicable to real-

world images as well, and they perform better than the state-of-the-art point correspondence-based techniques.

1 INTRODUCTION

Although computer vision has been an intensively

researched area in computer science from many

decades, several unsolved problems exist in the ﬁeld.

The main task of the research behind this paper is to

discover the relationship among the afﬁne transfor-

mation, the homography, the epipolar geometry, and

the projection matrices using the fundamental formu-

lation introduced in the pioneering work of Molnar

at al. (Moln

ar and Chetverikov, 2014) in 2014. The

aim of this study is to show how this theory can be

applied to solve real-life computer vision tasks like

estimating the homography and afﬁne transformation

between planar patches more accurately than it can

be done by classical methods (Hartley and Zisserman,

2003).

A two-dimensional point in an image can be rep-

resented as a 3D vector, it is called the homogeneous

representation of the point. It lies on the projective

plane P

. The homography is an invertible mapping

of points and lines on the projective plane P

. Other

terms for the transformation include collineation, pro-

jectivity, and planar projective transformation. (Hart-

ley and Zisserman, 2003) provide a speciﬁc deﬁni-

tion: A mapping P

→ P

is a projectivity if and only

if there exists a non-singular 3× 3 matrix H such that

for any point in P

represented by vector x it is true

that its mapped point equals Hx.

The correspondence can also be formalized for 2D

lines as l

−T

l where line parameters can be written

as vectors l and l

on the ﬁrst and second images, re-

spectively. If a point p lies on line l, the transformed

location x

must lie on the corresponding line l

It is a very exciting fact that the concept of ho-

mography was already known in the middle of the last

century (Semple and Kneebone, 1952).

There are many approaches in the ﬁeld to esti-

mate homography between two images as it is sum-

marized in (Agarwal et al., 2005). At ﬁrst, we have

to mention the simplest method called Direct Linear

Transform (Hartley and Zisserman, 2003) (DLT). In

that case one wishes to estimate 8 unknown param-

eters of the homography H based on known point

correspondences by solving an overdetermined sys-

tem of equations generated from the linearization of

the basic relationship x

∼ Hx, where the operator ∼

means equality up to scale. The linearization itself

434

Barath, D. and Hajder, L.

Novel Ways to Estimate Homography from Local Afﬁne Transformations.

DOI: 10.5220/0005674904320443

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 434-445

ISBN: 978-989-758-175-5

distorts the noise, therefore optimization for the orig-

inal nonlinear projective equations gives more accu-

rate results. This can be done by numerical optimiza-

tion techniques such as the widely used Levenberg-

Marquardt (Marquardt, 1963) optimization. How-

ever, the linear algorithms can also be enhanced if

data normalization (Hartley and Zisserman, 2003) is

applied ﬁrst.

(Kanatani, 1998) proposed a method to minimize

the estimation error within the Euclidean framework

since the noise occurs in image coordinates and not in

abstract higher dimensional algebraic spaces.

Obviously, there are many other ways to esti-

mate the homography: line-based (Murino et al.,

2002), conic-based (Kannala et al., 2006; Mudigonda

et al., 2004), contour-based (Kumar et al., 2004) and

patch-based (Kruger and Calway, 1998) methods ex-

ist. However, the matching of these features is not as

easy as that of points. Nowadays, there are very efﬁ-

cient feature point matchers (Morel and Yu, 2009).

Despite the fact that so many kind of homography

estimation techniques available in the ﬁeld, we have

not ﬁnd any dealing with local afﬁne transformation-

based homography estimation.

Application of Homographies. There are many

cases in computer vision where homography is re-

quired. First of all, one has to write about camera

calibration (Zhang, 2000). If the homographies be-

tween the 3D chessboard coordinates and the pro-

jected ones is computed for several images, then the

intrinsic camera parameters can be computed as it is

proved by (Zhang, 2000).

Camera calibration is the process of determining

the intrinsic and extrinsic parameters of the camera,

where intrinsic parameters are camera-speciﬁc: focal

length, lens distortion, and the principal point. Extrin-

sic parameters describe the camera orientation, and its

location in 3D space.

Estimation of surface normals is also an impor-

tant application of plane-plane homographies. If the

homography is known between the images of a plane

taken by two perspective cameras, then the homog-

raphy can be decomposed into camera extrinsic pa-

rameters, the plane normal, and the distance of the

plane w.r.t. the ﬁrst camera (Faugeras and Lustman,

1988; Malis and Vargas, 2007). Molnar et al. (Moln

et al., 2014) and Barath et al. (Barath et al., 2015)

showed that the afﬁne transformation is enough in or-

der to compute the surface normal, and it can be com-

puted from the homography by derivating that as it is

described in the appendix.

A very important application area of homography

estimation is to build 3D models of scenes where

relatively large ﬂat planes are present. Typical ex-

ample for such tasks is the reconstruction of urban

scenes that is a challenging and long-researched prob-

lem (Musialski et al., 2012; Tan

acs et al., 2014).

Nowadays, 3D reconstruction pipelines uses point

correspondences to compute the sparse (Agarwal

et al., 2011; Pollefeys et al., 2008) or dense (Fu-

rukawa and Ponce, 2010; Vu et al., 2012) reconstruc-

tion of the scenes. However, patch-based approaches

has recently proposed (B

odis-Szomor

u et al., 2014;

Tan

acs et al., 2014).

The main contributions of the paper are as follows.

The ﬁrst part of the paper deals with homography es-

timation when the fundamental matrix is unknown.

In this case, the afﬁne parameters can be calculated

from corresponding patches in stereo images. (i) It is

described that the homography can robustly be esti-

mated using the afﬁne transformations. In the second

part, we focus on the presence of the known funda-

mental matrix. (ii) It is proven that the homography

can be calculated only from one point correspondence

and the related afﬁne transformation if the epipolar

geometry is known. Finally, a novel algorithm is de-

scribed. (iii) We show here that homography can be

estimated using only two point correspondences and

the neighboring image patches if the cameras are fully

calibrated.

2 METHODS TO ESTIMATE

HOMOGRAPHY FROM AFFINE

TRANSFORMATION

The main contribution of this paper is to introduce dif-

ferent techniques in order to estimate the homography

if afﬁne transformations are known at different loca-

tions. We also show here that more efﬁcient estima-

tors can be formed if the epipolar geometry is known

as well. The main geometric terms and concepts are

summarized in this section ﬁrst.

2.1 THEORETICAL BACKGROUND

Homography and Afﬁne Transformation. The

standard deﬁnition of homography is applied here

which was mentioned in the introduction: a homog-

raphy H is the mapping P

→ P

which maps each

vector x

(1)

= [u

(1)

]

to its corresponding location

(2)

= [u

(2)

]

as [u

(2)

,1]

∼ H[u

(1)

,1]

(The upper and lower indices denote the index of the

current image, and the number of the current feature

point, respectively.) (Moln

ar and Chetverikov, 2014)

Novel Ways to Estimate Homography from Local Afﬁne Transformations

435

showed that the afﬁne transformation

A =





(1)

can be expressed from the parameters of the homo-

graphies as it is discussed in the appendix. These four

parameters are responsible for horizontal and verti-

cal scales, shear and rotation. The last column of the

afﬁne transformation A gives the offset.

Extracting Homography with Fundamental Ma-

trix. Relationship, which is well-known from epipo-

lar geometry (Hartley and Zisserman, 2003) led us to

make estimation process easier, and decrease the DoF

of the problem if the fundamental matrix is known.

This relationship is formulated as follows (Hartley

and Zisserman, 2003):

(2)

H = λF (2)

where e

(2)

= [e

(2)

,1]

denotes the epipole in the

second image, and λ is the scale of the fundamental

matrix F. The operator [v]

is the well-known matrix

formula representing the cross product with vector v.

Remark that the rank of matrix [v]

is two, therefore

the third row of the matrix can be determined as the

linear combination of the ﬁrst two ones.

The basic relationship deﬁned in Eq. 2 shows how

the knowledge of fundamental matrix decreases the

DoF of the estimation problem. The last row is re-

dundant as the rank of [e

(2)

]

is two. Therefore, only

the ﬁrst two rows contain useful information. They

can be written as



0 −1 e

1 0 −e











= (3)





This equation shows that the DoF can be reduced

to 3 since the elements in the ﬁrst two rows of the

homography can be expressed by those in the third

one (h

, and h

), if the fundamental matrix is

known:

= e

+ λ f

= e

+ λ f

= e

+ λ f

= e

− λ f

(4)

= e

− λ f

= e

− λ f

Remark that both the fundamental matrix and the

homography are determined up to an arbitrary scale.

Therefore, one scale is allowed to be set to an arbi-

trary value. In our algorithms, λ = 1.

If Equation 4 is substituted into the relationship

of the DLT method (p

(2)

∼ H p

(1)

), then the homog-

raphy can be computed. Remark that one point pair

gives only one equation as the fundamental matrix re-

duces the DoF of the correspondence problem to one

since the point pairs have to lie on the related epipolar

lines. This homography estimation method is called

3PT in this study because the estimation can be car-

ried out if at least three point correspondences (and

the fundamental matrix) are given.

2.2 Homography Estimation from

Afﬁne Transformation (HA)

Based on the elements of the afﬁne matrix a linear

system of equations can be formed. The relationship

between the afﬁne transformation A

belonging to the

i-th point pair and the corresponding homography is

discussed in the appendix. For the linearization, the

Eqs. 9, 11- 13 have to be multiplied by the projective

depth s (see Eq. 10). The obtained linear equations

are as follows:

− h



(2)

+ a

i,11

(1)



(5)

−h

i,11

(1)

− h

i,11

= 0

− h



(2)

+ a

i,12

(1)



−h

i,12

(1)

− h

i,12

= 0

− h



(2)

+ a

i,21

(1)



−h

i,21

(1)

− h

i,21

= 0

− h



(2)

+ a

i,22

(1)



−h

i,22

(1)

− h

i,22

= 0

Thus, the estimation can be written as a homoge-

nous system of linear equations. However, all the el-

ements of homography H cannot be estimated since

elements h

, and h

are not present in the equations.

This is trivial as these elements code the offset of the

planes. Fortunately, the well-known (Hartley and Zis-

serman, 2003) Direct Linear Transformation (DLT)

method can compute the offset as well. It gives two

additional linear equations for the elements of the ho-

mography. They are as follows:

(1)

+ h

(1)

+ h

− h

(1)

(2)

− (6)

(1)

(2)

− h

(2)

= 0

(1)

+ h

(1)

+ h

− h

(1)

(2)

−

(1)

(2)

− h

(2)

= 0

Equations 5, and 6 give the linear relationship among

the elements of the afﬁne transformation, homogra-

phy, and point locations. Six equations are obtained

for each point correspondence. They can be written

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

436

B =







1 0 0 0 0 0 −



(2)

+ a

i,11

(2)



i,11

(1)

−a

i,11

0 1 0 0 0 0 −a

i,12

(1)

−



(2)

+ a

i,12

(2)



−a

i,12

0 0 0 1 0 0 −



(2)

+ a

i,21

(1)



−a

i,21

(1)

−a

i,21

0 0 0 0 1 0 −a

i,11

(1)

−



(2)

+ a

i,22

(1)



−a

i,22

(1)

1 0 0 0 −u

(1)

(2)

−v

(1)

(2)

−u

(2)

0 0 0 u

(1)

1 −u

(1)

(2)

−v

(1)

(2)

−v

(2)







(7)

h = [h

]

as a homogeneous linear form Bh = 0 where the vec-

tor h, and matrix B contain the elements of the ho-

mography, and the corresponding coefﬁcients, respec-

tively. They are expressed in Eq. 7. The optimal so-

lution (Bj

orck, 1996) subject to |h| = 1 is obtained as

the eigenvalue of B

B corresponding to the smallest

eigenvalue. If at least two point correspondences are

given, the homography can be estimated. This is a

notable advantage of HA algorithm compared to the

classical DLT one as the latter one requires at least

four correspondences.

2.3 Homography Estimation from

Afﬁne Transformation with Known

Fundamental Matrix (HAF)

In this section, we show that the estimation method

becomes much simpler if the epipolar geometry is

known. Equation 4 shows the basic relationship of

the plane-plane homography and the epipolar geom-

etry of the stereo camera setup. The afﬁne transfor-

mation can be computed from the homography. (It

is written in the appendix in detail.) By considering

both relationship, the estimation of homography can

also be written in a linear form even if the epipolar

geometry is known. It is as follows:



i,11

(1)

+ u

(2)

− e



i,11

(1)

+ h

i,11

= f



i,12

(1)

+ u

(2)

− e



i,12

(1)

+ h

i,12

= f



i,21

(1)

+ v

(2)

− e



i,21

(1)

+ h

i,21

= − f



i,22

(1)

+ v

(2)

− e



i,22

(1)

+ h

i,22

= − f

This is an inhomogeneous system of linear equations,

thus it can be formed as Cy = d , where matrix C

consists of the coefﬁcients, d = [ f

, f

,− f

]

while y = [h

]

is the vector of the unknown

parameters. The optimal solution in the least squares

sense is given by y = C

†

d where C

†

is the Moore-

Penrose pseudo-inverse of matrix C. The elements of

matrix C are as follows:



i,11

(1)

+ u

(2)

− e



= a

i,11

(1)

= a

i,11

= a

i,12

(1)



i,12

(1)

+ u

(2)

− e



= a

i,12



i,21

(1)

+ v

(2)

− e



= a

i,21

(1)

= a

i,21

= a

i,22



i,22

(1)

+ v

(2)

− e



= a

i,22

(8)

This method gives an overdetermined system for only

one corresponding point pair, and an afﬁne transfor-

mation. More equations can be added trivially to the

system. It means, that if one has only a single point

pair and the related afﬁne transformation, one is able

to compute the homography. Of course, it can be eas-

ily completed by other methods (e.g. DLT algorithm)

exactly the same way as we showed in the previous

section.

2.4 Improvements

Nonlinear Reﬁnement. The methods proposed here

are solved by linear algorithms since the original

problems are linearized by multiplying with the de-

nominator. However, this multiplication distorts the

original signal-noise ratio. If the denominator is rel-

atively small, the distortion can be signiﬁcant. For

this reason, the nonlinear version of the proposed al-

gorithms have to be formed. We used the classi-

cal Levenberg-Marquardt (Marquardt, 1963) numeri-

cal technique in order to compose nonlinear methods.

To distinguish the linear and nonlinear versions of the

methods, the names of the linear versions begin with

’LIN’.

Normalization. Normalization of the input data is

usual in homography estimation (Hartley and Zisser-

Novel Ways to Estimate Homography from Local Afﬁne Transformations

437

man, 2003). Here we show how the normalized coor-

dinates and the normalized afﬁne transformation can

be obtained.

Let us denote the normalizing transformations

which are applied to the 2D point clouds in each im-

age with T

, and T

. The normalized points are calcu-

lated on the ﬁrst, and second images as p

(1)

= T

(1)

and p

(2)

= T

(2)

, respectively.

It is not enough to normalize only the points, both

the fundamental matrix and the afﬁne transformations

have to be normalized. The normalization formula for

the fundamental matrix can be written (Hartley and

Zisserman, 2003) as F

= T

−T

−1

The afﬁne transformations can also be normalized,

as it is described in the appendix in details.

To distinguish the normalized versions of the

methods, the names of the normalized algorithms be-

gin with ’Norm.’.

Robustiﬁcation. It is unavoidable in real application

that the input dataset contains both inliers and out-

liers. We apply the RANSAC (Fischler and Bolles,

1981) paradigm in order to make the proposed meth-

ods robust. The names of RANSAC-based methods

contain the word ’RSC’.

2.5 Theoretical Contribution

It can be seen from the theory of HAF algorithm

that if the fundamental matrix is known, then the ho-

mography and the afﬁne transformation can unequiv-

ocally be calculated from each other in an observed

point. This property of perspective projection states

that afﬁne-invariance is equivalent to perspective-

invariance if the epipolar geometry is known between

stereo images. In order to take the advantages of this

property, fully calibrated camera setup is not needed,

only the fundamental matrix between the cameras is

required.

3 Homography Estimation based on

Photo-consistency and Point

Correspondences (RHE – Rotary

Homography estimation)

The homography estimation (Agarwal et al., 2005)

can be carried out using usual features in images such

as point or line correspondences. Another approach

is to use pixel intensities to estimate the plane-plane

transformation between image patches (Habbecke

and Kobbelt, 2006; Z. Megyesi and D.Chetverikov,

2006; Tan

acs et al., 2014). The study of (Habbecke

Figure 1: Rotating plane.

and Kobbelt, 2006) proposes to estimate the four

spatial plane parameters, while (Z. Megyesi and

D.Chetverikov, 2006) and (Tan

acs et al., 2014) reduce

the DoF of plane estimation problem to three using

rectiﬁed images. Remark that rectiﬁcation can be car-

ried out if the fundamental matrix is known, the two

projection matrices themselves does not have to be

known.

Other possible solution is to use point correspon-

dences in order to compute the homography (Hart-

ley and Zisserman, 2003). If the fundamental ma-

trix is known, the estimation can be calculated from

three correspondences. If the epipolar geometry is not

known, four points are required at least.

We show here that homography can also be es-

timated if both point correspondences and photo-

consistency are considered. For the algorithm pro-

posed in this section, two point correspondences are

taken. The projection matrices of the stereo images

are known, therefore, the spatial coordinates of the

two points can be calculated via triangulation (Hart-

ley and Sturm, 1997).

It is trivial that three spatial points determine the

plane as they are enough to determine the homogra-

phy. Two of those are calculated by triangulation, the

remaining task is to determine the third one. The

DoF of the problem is only one since an angle α

(∈ (0,π]) determines the plane as it is visualized in

Fig. 1. This angle is determined via a brute-force (ex-

haustive) search in our approach. For each candidate

value α, a spatial patch can be formed that consists of

the two triangulated points p

and p

, and the angle

of the patch is α. The cameras are calibrated, there-

fore the homographies between the projected patches

can be calculated. Then this homography is evalu-

ated. Its score is calculated as the similarity

of the

corresponding pixels around the projected locations

of points p

and p

. (The pixel correspondences are

obtained by the homography.) The 3D patch with the

highest similarity score gives the best estimation for

We use normalized cross correlation (Sonka et al.,

2007) (NCC) for this purpose.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

438

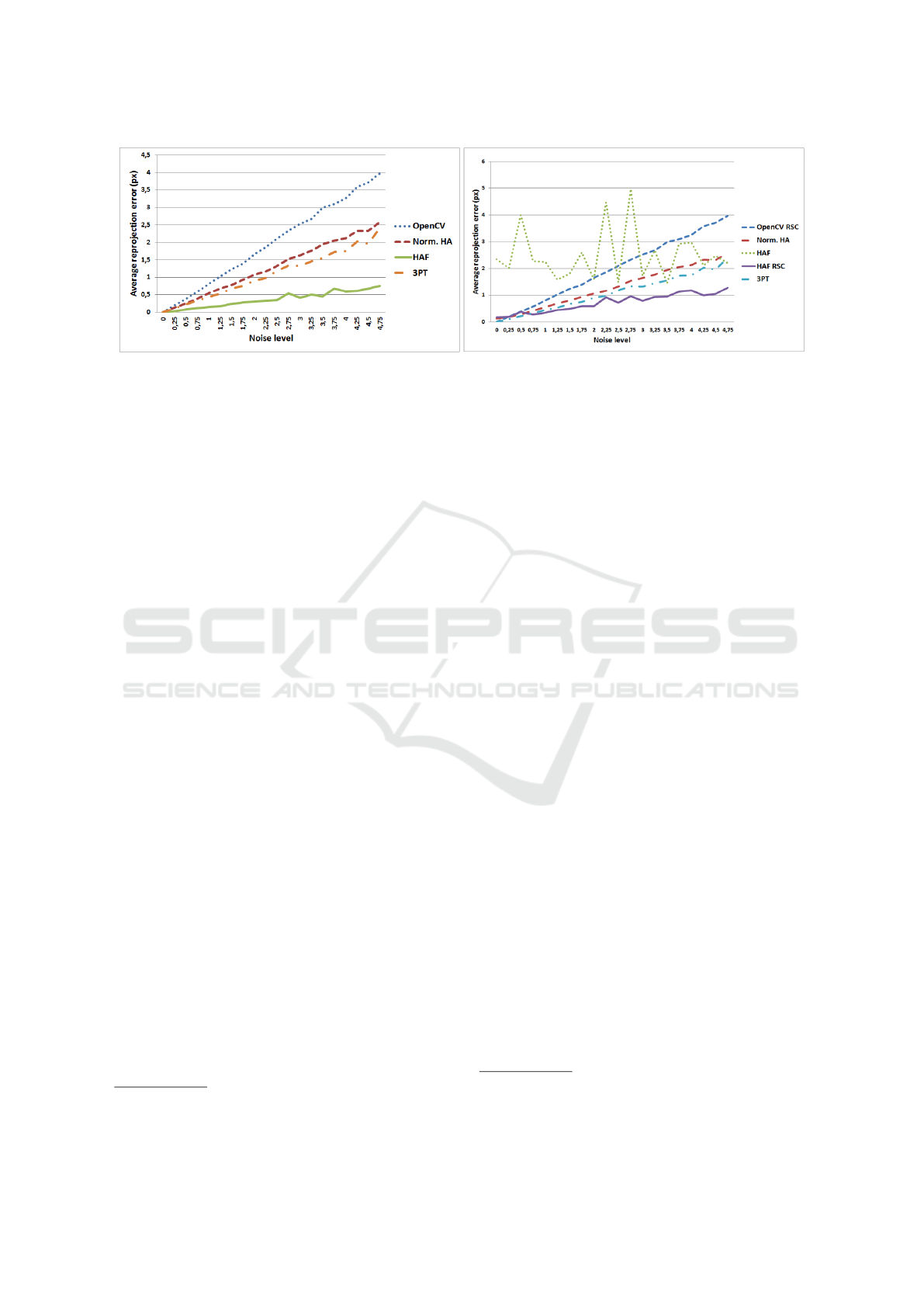
Figure 2: The left and right plots shows the average errors of the methods with noisy point coordinates and noisy afﬁne trans-

formation, respectively. The vertical axis are the average reprojections errors in pixels. The horizontal ones are the σ (spread)

of the Gaussian-noise added to point coordinates. Afﬁne error appears by multiplying the original afﬁne transformation with

a relatively small random transformation.

the 3D patches. The obtained homography is deter-

mined by this 3D patch.

The proposed algorithm is as follows:

1. Calculate point p

related to the current α value,

and the homography H

. Then for the i-th (i ∈

[1,2]) point pair compute A

α,i

between the vicini-

ties of the point projection using H

2. Compute the similarity (NCC) related to each

point and afﬁne transformation. If the sum of the

similarities in the two observed points is greater

than the currently best candidate then α

opt

:= α.

3. If α < π increase α, and continue from Step 2.

Otherwise, terminate with H

4 EXPERIMENTAL RESULTS

The proposed homography estimators are tested both

on synthesized data and real world images.

4.1 Test on Synthesized Data

The main goal of the tests is to generate different

cases where homographies have to be estimated. For

this reason, a stereo image pair represented by pro-

jection matrices is generated ﬁrst. Their orientation

are constrained, and the positions are randomized

a 30 × 30 plane that is 60 unit far from the origin on

axis Z. The generated cameras look at the origin. The

remaining one DoF of the camera orientation is ran-

domized as well. Then a 3D plane is generated at the

origin with a random normal vector. Then 50 points

We applied zero-mean Gaussian noise for random num-

ber generation.

are randomly sampled, and they are perspectively pro-

jected onto the two cameras. The ground truth ho-

mography between the projections of the plane is cal-

culated as well.

The error values are deﬁned as the average/median

reprojection errors of the points.

All the proposed methods are tested

in the syn-

thesized environment except for the RHE which re-

quires real images for photo-consistency calculation.

For each test, 100 different planes are generated on

every noise level.

The proposed methods are compared to the

OpenCV-implemented ‘ﬁndHomography’ function,

which is a normalized DLT algorithm (Hartley and

Zisserman, 2003) and a reﬁnement stage using

Levenberg-Marquardt algorithm (Marquardt, 1963)

that minimizes the reprojection error. The other ri-

val method is the normalized 3PT. The latter one is

implemented by us.

Test with Noisy Point Coordinates. In the ﬁrst

test case, 2D point coordinates are contaminated by

zero-mean Gaussian noise, but the afﬁne transforma-

tions do not. Two kinds of methods can be seen in

the left plot of Fig 2: the ﬁrst one uses the funda-

mental matrix, the second one does not. Within the

ﬁrst group, it can be observed that normalized HA

performs better than OpenCV implementation. The

second group which uses the fundamental matrix con-

sists of HAF algorithm and the normalized three point

(3PT) method. It can be seen that HAF performs sig-

niﬁcantly better.

Test with Noisy Afﬁne Transformations. The

next test case (left plot of Fig. 2) is with noisy afﬁne

transformations. Noise in the afﬁne transformation

All the tests have been implemented both on Mat-

lab, and C++. It can be downloaded from webpage

http://web.eee.sztaki.hu

Novel Ways to Estimate Homography from Local Afﬁne Transformations

439

appeares as a nearly identity random transformation.

Every afﬁne matrix is multiplied with such a trans-

formation. Note that the horizontal axis in the charts

shows only the noise of point coordinates. It can be

seen that the original HAF is very sensitive to the

afﬁne noise, however, its RANSAC version balances

this behaviour.

Figure 3: The average reprojection errors of the variants

of HA, and HAF method are shown in the top, and bot-

tom rows, respectively. The point are contaminated by

Gaussian-noise, which σ value is denoted by the horizon-

tal axis. The vertical one shows the average error in pixels.

In the top plot of Fig 3, the variants of HA can

be seen with contaminated point coordinates. It is

evident that the normalized, numerically reﬁned ver-

sion gives the most accurate result. The bottom ﬁgure

shows the different versions of the HAF. The normal-

ized HA is also visualized for the sake of comparison.

The average error seems to be very chaotic, however,

the numerically reﬁned version seems to be the best.

It is unequivocal that the proposed methods give

more accurate results than the rival ones. Without

the knowledge of the epipolar geometry, the normal-

ized version of HA method performs better than the

numerically reﬁned normalized DLT. All methods is

outperformed by HAF.

4.2 Test on Real Data

Our algorithms are tested on the sequences of Oxford

dataset

Calculation of the Afﬁne Transformation for Real

Tests. In order to apply the proposed algorithms to

real data, the knowledge of the afﬁne transforma-

tion is required between every single point correspon-

dences. There are several ways to compute the afﬁne

transformation: brute-force algorithms, or afﬁne in-

variant feature trackers (Mikolajczyk and Schmid,

2004). During our experiments the following method

is used:

(1.) Big planar surfaces are segmented using se-

quential RANSAC. For each planar patch the con-

tained 2D point cloud are triangulated by Delaunay

triangulation (B., 1934; Lee and Schachter, 1980).

(2.) Then, for each point pair we iterate through all

the corresponding triangles. The homography is com-

puted between every triangle pair (on the ﬁrst and

the second images) using 3PT method, then the afﬁne

transformation is decomposed from that as it is de-

scribed in the appendix. (3.) This method computes

many slightly different afﬁne transformations for ev-

ery single point pair. Remark that all of them are used

during the homography estimation as an overdeter-

mined system of equations.

To visualize the quality of the proposed algo-

rithms, the surface normals are computed, and they

are drawn into the images. There are several normal

estimators (Faugeras and Papadopoulo, 1998; Malis

and Vargas, 2007; Barath et al., 2015) in the ﬁeld,

we choose the method of Barath et al. (Barath et al.,

2015) due to its efﬁciency and simplicity. This es-

timator calculates the surface normal from the afﬁne

transformation related to the observed point instead

of the homography in order to avoid the ambiguity of

the homography decomposition (He, 2012).

The Oxford data set contain point correspon-

dences, but we use ASIFT method (Morel and Yu,

2009) to detect and track points instead of the original

data. The Hartley-Sturm triangulation (Hartley and

Sturm, 1997) is applied to each point pair ﬁrst. Pla-

nar regions are selected using sequential RANSAC,

however, it could be done by J-Linkage (Toldo and

Fusiello, 2010), or other multi-homography ﬁtting al-

gorithm as well. Then fundamental matrix are cal-

culated by the RANSAC 8-point technique (Hart-

ley and Zisserman, 2003). The tests are both qual-

itatively and quantitatively evaluated. For the latter

one, the error values are calculated as follows: 50%

of the point correspondences are separated, and the

Dataset can be downloaded from http://www.robots.

ox.ac.uk/∼vgg/data/data-mview.html

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

440

homography is computed using only them. Then the

reprojection error of the homography is computed for

all the features. The ﬁnal value was the RMS (Root

Mean Squares) of the errors.

Another error metric have to be used for testing

the RHE method. RHE computes the homography

from only two feature correspondences. Therefore,

the edges of the mentioned Delaunay triangulation

are chosen as point pairs, and the homography related

to the pair is computed by RHE. Then the reprojec-

tion error of every homography is calculated for all

the feature points. The ﬁnal reprojection error of the

method is calculated as the average of these errors.

In the following comparisons, the minimum reprojec-

tion error is also shown. Note that photo-consistency

calculation processed on patches are of sizes from

60 × 60 up to 120 × 120.

Figure 4 shows an example that demonstrates how

the homography can be estimated by the proposed

methods using many feature points. In this example,

the baseline of the stereo setup is short, and the two

main walls are segmented. The list of the obtained re-

projection errors is written in Table 1. It is clear that

the proposed algorithms (HA and HAF) outperform

the rival ones (robust version of 3PT and OpenCV

methods). HAF gives more accurate reconstruction

than HA since it uses the fundamental matrix as ad-

ditional information for the estimation. The obtained

surface normals are perpendicular to each other (see

the bottom of Fig. 4) as it is expected.

Delaunay triangulation is applied to the points of

each wall (see the top of Fig. 4). Then RHE algo-

rithm runs on every edge. The reprojection error of

each estimated homography is calculated w.r.t. to ev-

ery point pair selected from the current planar patch

(both for the walls ’Left’ and ’Right’). From the aver-

age of these reprojection errors, this algorithm yields

less accurate results since it is calculated using only

two point pairs. Even so, we have many estimated ho-

mographies (one for each edge of the triangulation)

and we choose the one with the lowest reprojection

error. It is turned out that it provides accurate estima-

tion. Its results are the best and second one among

all the other methods for the ’Left’ and ’Right’ walls,

respectively.

The next two examples are seen in Figures 5 and 6.

The ﬁrst one is the sequence ’Model House’. The

segmentation ﬁnds two large planes on the scene: the

wall and the ground. The next normal reconstruction

example is called the sequence ’Library’. Two large

planes are found in this scene: the wall and the roof.

Then the proposed and rival homography estimators

are applied. The normals reconstructed by the RHE

algorithm are visualized in these ﬁgures, therefore the

Figure 4: The top row visualize the delaunay triangulation

of the points. The bottom row shows reconstructed surface

normals using homography of large walls on sequence ’Col-

lege’.

Table 1: Reprojection errors (px) for sequence ’College’.

Left Right

OpenCV RSC 3.824 2.668

3PT RSC 3.586 2.604

HA RSC 3.589 1.759

HAF RSC 3.585 1.677

RHE AVG 7.881 8.768

RHE MIN 3.442 1.692

estimated normals are independent of each other.

The proposed and rival homography estimators

are compared in Table 2. (Note that the patch size of

the RHE algorithm was set to 60 × 60 for sequences

’Building’ and ’Model House’.) It is clear that the

proposed methods outperform the rival ones in these

cases. The HAF algorithm yields the best results ex-

cept for only one example when HA method is the

most accurate.

Table 2: Reprojection errors (px) for sequences ’Model

House’ and ’Library’.

Model House Library

Wall Ground Wall Roof

OpenCV RSC 1.554 2.750 1.422 1.693

3PT RSC 1.400 1.569 1.513 1.399

HAF RSC 0.864 1.635 1.317 1.320

HA RSC 0.759 1.736 1.338 1.422

RHE Avg. 2.911 4.819 7.889 2.445

RHE Min. 0.780 2.378 1.384 1.514

The proposed methods are tested on 60 different

planes, as it is shown in Table 3. The showed value is

as follows: for every test plane homography is calcu-

lated by all the examined methods. Then the reprojec-

Novel Ways to Estimate Homography from Local Afﬁne Transformations

441

Figure 5: Reconstructed surface normals using RHE algo-

rithm on sequence ’Model House’. Left: reconstructed wall

Right: reconstructed ﬂoor. Top: ﬁrst image. Bottom: sec-

ond image.

Figure 6: Reconstructed surface normals using RHE al-

gorithm on sequence ’Library’. Left: reconstructed wall

Right: reconstructed roof. Top: ﬁrst image. Bottom: sec-

ond image.

tion error of the homography computed by OpenCV

is labeled with 100%. Other values in the table such

as 66% related to HAF, means that the ratio of the

average reprojection errors of HAF and OpenCV is

0.66.

4.3 Processing Times

The processing time of each method is discussed here.

HA and HAF methods are based on the solution of a

homogeneous, and inhomogeneous linear system of

equations, respectively. These systems consists of 6

and 4 equations per point pair. Therefore, HA is a bit

slower than DLT, however, not signiﬁcantly. HAF is

as fast as DLT since the equation number per point is

equal.

Even though, RHE is a numerical optimization in

a 1-DoF search space, our implementation is not ap-

plicable to online tasks since its processing time is

Table 3: Error percentage compared to OpenCV on 60 dif-

ferent planes.

OpenCV 3PT HA HAF RHE

Avg.

RHE

Min.

100% 79% 67% 66% 119% 57%

around half a second. However, it could be paral-

lelised on GPU straighforwardly.

5 CONCLUSION

Novel homography estimator methods (HA and HAF)

have been proposed here that can estimate the homog-

raphy if the afﬁne transformations are known between

the surrounding regions of the corresponding point

pairs. We have also proposed an algorithm to estimate

the homography based on both point correspondences

and photo-consistency.

HA method does not need the knowledge of

epipolar geometry, however, it gives better results

than the standard homography estimation techniques

in most of the situations. As a minimal problem, it

is computable from only two point correspondences

and the related afﬁne transformations. The HAF al-

gorithm requires the knowledge of the fundamental

matrix, and at least one point correspondence and the

related afﬁne transformation have to be known to cal-

culate the homography. It is usually the most efﬁ-

cient method. Their RANSAC variants are recom-

mended to use for contaminated input data, because

afﬁne transformations are signiﬁcantly more sensitive

to noise than point correspondences.

It is proven that afﬁne-invariance is equivalent to

perspective-invariance in the case of known funda-

mental matrix. We think it is a signiﬁcant contribution

to the theory of 3D stereo vision.

The novelty of the proposed RHE algorithm is to

reduce homography estimation to a one-dimensional

search in a half unit circle when both point correspon-

dences and camera parameters are known. The simi-

larity function for the minimization problem is based

on photo-consistency.

The synthetic and real tests have shown that all

the proposed methods (HA and HAF) give more ac-

curate results and use similar amount of resources as

the state-of-the-art point correspondence-based tech-

niques. Therefore the novel and standard algorithms

can be easily replaced for each other. RHE algorithm

also gives appropriate results using only two corre-

sponding point pairs. Moreover, RHE gives accurate

estimation in ofﬂine applications by repeating the op-

timization for many possible pairings. Then the point

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

442

pair which supplies the best homography by RHE are

usually more accurate than the results of all the other

methods. It is important to note that if many point

correspondences (hundreds of points) are given from

the observed plane, the original point-based homog-

raphy estimation methods give nearly the same result

as the proposed ones.

ACKNOWLEDGEMENTS

The research was partially supported by the Hungar-

ian Scientiﬁc Research Fund (OTKA No. 106374).

REFERENCES

Agarwal, A., Jawahar, C., and Narayanan, P. (2005). A Sur-

vey of Planar Homography Estimation Techniques.

Technical report, IIT-Hyderabad.

Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Curless,

B., Seitz, S. M., and Szeliski, R. (2011). Building

rome in a day. Commun. ACM, 54(10):105–112.

B., D. (1934). Sur la sphere vide. Izvestia Akademii

Nauk SSSR, Otdelenie Matematicheskikh i Estestven-

nykh Nauk, 7:793–800.

Barath, D., Molnar, J., and Hajder, L. (2015). Optimal Sur-

face Normal from Afﬁne Transformation. In VISAPP

2015, pages 305–316.

orck,

A. (1996). Numerical Methods for Least Squares

Problems. Siam.

odis-Szomor

u, A., Riemenschneider, H., and Gool, L. V.

(2014). Fast, approximate piecewise-planar modeling

based on sparse structure-from-motion and superpix-

els. In IEEE Conference on Computer Vision and Pat-

tern Recognition.

Faugeras, O. and Lustman, F. (1988). Motion and struc-

ture from motion in a piecewise planar environment.

Technical Report RR-0856, INRIA.

Faugeras, O. D. and Papadopoulo, T. (1998). A Nonlin-

ear Method for Estimating the Projective Geometry of

Three Views. In ICCV, pages 477–484.

Fischler, M. and Bolles, R. (1981). RANdom SAmpling

Consensus: a paradigm for model ﬁtting with appli-

cation to image analysis and automated cartography.

Commun. Assoc. Comp. Mach., 24:358–367.

Furukawa, Y. and Ponce, J. (2010). Accurate, dense, and

robust multi-view stereopsis. IEEE Trans. on Pattern

Analysis and Machine Intelligence, 32(8):1362–1376.

Habbecke, M. and Kobbelt, L. (2006). Iterative multi-view

plane ﬁtting. In Proceeding of Vision, Modelling, and

Visualization, pages 73–80.

Hartley, R. I. and Sturm, P. (1997). Triangulation. Computer

Vision and Image Understanding: CVIU, 68(2):146–

157.

Hartley, R. I. and Zisserman, A. (2003). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press.

He, L. (2012). Deeper Understanding on Solution Ambigu-

ity in Estimating 3D Motion Parameters by Homogra-

phy Decomposition and its Improvement. PhD thesis,

University of Fukui.

Kanatani, K. (1998). Optimal homography computation

with a reliability measure. In Proceedings of IAPR

Workshop on Machine Vision Applications, MVA,

pages 426–429.

Kannala, J., Salo, M., and Heikkil, J. (2006). Algorithms for

computing a planar homography from conics in cor-

respondence. In Proceedings of the British Machine

Vision Conference.

Kruger, S. and Calway, A. (1998). Image registration using

multiresolution frequency domain correlation. In Pro-

ceedings of the British Machine Vision Conference.

Kumar, M. P., Goyal, S., Kuthirummal, S., Jawahar, C. V.,

and Narayanan, P. J. (2004). Discrete contours in mul-

tiple views: approximation and recognition. Image

and Vision Computing, 22(14):1229–1239.

Lee, D.-T. and Schachter, B. J. (1980). Two algorithms

for constructing a delaunay triangulation. Interna-

tional Journal of Computer & Information Sciences,

9(3):219–242.

Malis, E. and Vargas, M. (2007). Deeper understanding of

the homography decomposition for vision-based con-

trol. Technical Report RR-6303, INRIA.

Marquardt, D. (1963). An algorithm for least-squares esti-

mation of nonlinear parameters. SIAM J. Appl. Math.,

11:431–441.

Mikolajczyk, K. and Schmid, C. (2004). Scale & afﬁne in-

variant interest point detectors. International journal

of computer vision, 60(1):63–86.

Moln

ar, J. and Chetverikov, D. (2014). Quadratic transfor-

mation for planar mapping of implicit surfaces. Jour-

nal of Mathematical Imaging and Vision, 48:176–184.

Moln

ar, J., Huang, R., and Kato, Z. (2014). 3d recon-

struction of planar surface patches: A direct solution.

ACCV Big Data in 3D Vision Workshop.

Morel, J.-M. and Yu, G. (2009). Asift: A new framework for

fully afﬁne invariant image comparison. SIAM Jour-

nal on Imaging Sciences, 2(2):438–469.

Mudigonda, P. K., Kumar, P., Jawahar, M. C. V., and

Narayanan, P. J. (2004). Geometric structure compu-

tation from conics. In In ICVGIP, pages 9–14.

Murino, V., Castellani, U., Etrari, A., and Fusiello, A.

(2002). Registration of very time-distant aerial im-

ages. In Proceedings of the IEEE International Con-

ference on Image Processing (ICIP), volume III, pages

989–992. IEEE Signal Processing Society.

Musialski, P., Wonka, P., Aliaga, D. G., Wimmer, M., van

Gool, L., and Purgathofer, W. (2012). A survey of

urban reconstruction. In EUROGRAPHICS 2012 State

of the Art Reports, pages 1–28.

Pollefeys, M., Nist

er, D., Frahm, J. M., Akbarzadeh, A.,

Mordohai, P., Clipp, B., Engels, C., Gallup, D., Kim,

S. J., Merrell, P., Salmi, C., Sinha, S., Talton, B.,

Wang, L., Yang, Q., Stew

enius, H., Yang, R., Welch,

G., and Towles, H. (2008). Detailed real-time urban

3d reconstruction from video. Int. Journal Comput.

Vision, 78(2-3):143–167.

Novel Ways to Estimate Homography from Local Afﬁne Transformations

443

Semple, J. and Kneebone, G. (1952). Algebraic Projective

Geometry. Oxford University Press.

Sonka, M., Hlavac, V., and Boyle, R. (2007). Image Pro-

cessing, Analysis, and Machine Vision. CENGAGE-

Engineering, third edition edition.

Tan

acs, A., Majdik, A., Hajder, L., Moln

ar, J., S

anta, Z.,

and Kato, Z. (2014). Collaborative mobile 3d recon-

struction of urban scenes. In Computer Vision - ACCV

2014 Workshops - Singapore, Singapore, November 1-

2, 2014, Revised Selected Papers, Part III, pages 486–

501.

Toldo, R. and Fusiello, A. (2010). Real-time incremen-

tal j-linkage for robust multiple structures estimation.

In International Symposium on 3D Data Processing,

Visualization and Transmission (3DPVT), volume 1,

page 6.

Vu, H.-H., Labatut, P., Pons, J.-P., and Keriven, R. (2012).

High accuracy and visibility-consistent dense multi-

view stereo. IEEE Trans. Pattern Anal. Mach. Intell.,

34(5):889–901.

Z. Megyesi, G. and D.Chetverikov (2006). Dense 3d re-

construction from images by normal aided matching.

Machine Graphics and Vision, 15:3–28.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22(11):1330–1334.

APPENDIX

Afﬁne Transformation from

Homography

The afﬁne parameters can be obtained from homog-

raphy between corresponding patches in stereo image

pairs. Let us assume that the homography H is given.

Then the correspondence between the coordinates in

the ﬁrst (u and v) and second (u

and v

) images is

written as

[u,v, 1]

where the 3 × 3 homography matrix H is written as

H =

















The afﬁne parameters come from the partial deriva-

tives of the perspective plane-plane transformation.

The top left element a

of afﬁne transformation ma-

trix is as follows:

∂u

[u,v,1]

−h

[u,v,1]

(

[u,v,1]

)

= (9)

−h

where

s = h

[u,v, 1]

(10)

The other components of afﬁne matrix are obtained

similarly

∂u

∂v

− h

(11)

∂v

∂u

− h

(12)

∂v

− h

. (13)

Normalization of Afﬁne

Transformation

Given corresponding point pairs x

(1)

and x

(2)

, the

goal is to determine the related afﬁne transforma-

tions if the points are normalized as x

0(2)

= T

(2)

and

0(1)

= T

(1)

. The normalization is the concatenation

of a scale and a translation. Therefore, the transfor-

mation matrices can be written as





(1)

0 t

(1)

0 s

(1)

0 0 1









(2)

0 t

(2)

0 s

(2)

0 0 1





. (14)

For an arbitrary 2D point x

(i)

= [u

(i)

] on the i-

th image, the transformed coordinates can be written

0(i)







(i)

0 t

(i)

0 s

(i)

0 0 1











(i)











(i)







If the homography of a plane is denoted by H using

the original coordinates, it connects the coordinates

on the ﬁrst and second image as x

∼ Hx

. If the nor-

malized coordinates are used, the relationship modi-

ﬁes as T

−1

0(2)

∼ HT

−1

0(1)

Therefore, the homography using the normalized

coordinates is H

= T

−1

. The deviations are writ-

ten in Eqs.15 – 18.

For the sake of simplicity, we do not determine the

last two elements of the ﬁrst row as they do not affect

the afﬁne transformation. They are denoted by stars

(’*’). The elements of the afﬁne transformation are

written in Eqs. 9 – 13. The normalized scale s

written as

(1)



0(1)

−t

(1)



(1)



0(1)

−t

(1)



= u

(1)

+ v

(1)

+ h

= s

Therefore, the normalization does not modify the

scale as it is expected. Now, the numerator for the ﬁrst

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

444

−1







1/s

(1)

0 −t

(1)

0 1/s

(1)

−t

(1)

0 0 1







(15)

= T

−1







(2)

0 t

(2)

0 s

(2)

0 0 1





















1/s

(1)

0 −t

(1)

0 1/s

(1)

−t

(1)

0 0 1







(16)







(2)













1/s

(1)

0 −t

(1)

0 1/s

(1)

−t

(1)

0 0 1







(17)







(2)

(1)

(2)

(1)

(2)

(1)

(2)

(1)

∗

(2)

(1)

(2)

(1)

(2)

(1)

(2)

(1)

∗

(1)

−h

(1)

− h

(1)

+ h







(18)

afﬁne transformation can be expressed as follows:

− h

0(2)

(2)

(1)

(2)

(1)

−

(1)



(2)



(2)

(1)

−

(2)

(1)

(2)

The other three components of the transformation can

be computed similarly:

− h

0(2)

(2)

(1)

−

(2)

(1)

(2)

− h

0(2)

(2)

(1)

−

(2)

(1)

(2)

− h

0(2)

(2)

(1)

−

(2)

(1)

(2)

By rearranging the equations the following formulas

are given:



(1)

+ h

(2)

+ h



(2)

(1)

−

(2)

(1)

(2)

(19)



(1)

+ h

(1)

+ h



(2)

(1)

−

(2)

(1)

(2)



(1)

+ h

(1)

+ h



(2)

(1)

−

(2)

(1)

(2)



(1)

+ h

(1)

+ h



(2)

(1)

−

(2)

(1)

(2)

These equations are linear w.r.t. the elements of the

homography. Therefore, these formulas compose a

homogeneous, linear system of equations. In order

to apply afﬁne normalization to the proposed meth-

ods, the equations refer to the afﬁne transformations

have to be replaced in the coefﬁcient matrix of each

method. For HAF a few modiﬁcations are required

beforehand. Formulas, which describe the connection

to the fundamental matrix (Eq. 4) have to substituted

into Eq. 19. The given equations are inhomogeneous

due to the elements of matrix F. After a few modiﬁca-

tions these can also be substituted into the coefﬁcient

matrix of HAF (Eq. 8).

Novel Ways to Estimate Homography from Local Afﬁne Transformations

445