
An External Memory Algorithm for the Minimum Enclosing Ball
Problem
Linus K
¨
allberg
1
, Evan Shellshear
2
and Thomas Larsson
1
1
M
¨
alardalen University, V
¨
aster
˚
as, Sweden
2
Fraunhofer Chalmers Centre, Gothenburg, Sweden
Keywords:
Minimum Enclosing Ball, Smallest Bounding Sphere, External Memory Algorithm, Big Data.
Abstract:
In this article we present an external memory algorithm for computing the exact minimum enclosing ball of a
massive set of points in any dimension. We test the performance of the algorithm on real-life three-dimensional
data sets and demonstrate for the first time the practical efficiency of exact out-of-core algorithms. By use of
simple heuristics, we achieve near-optimal I/O in all our test cases.
1 INTRODUCTION
External memory algorithms have become an essen-
tial part of data collection and processing due to the
inexorable data flood engulfing today’s applications.
Each year the amount of data collected increases, and
in 2020 the world’s data content is estimated to reach
44 zettabytes (IDC, 2014). Thus, it is clear that big
data skills are becoming essential, and that old algo-
rithms need to be adapted for the data deluge.
A key part of many external memory problems is
the minimum enclosing ball (MEB) problem. The
problem is to find the ball (or circle or sphere) with
minimum radius enclosing a given set of objects, such
as points or balls. Such a functionality is essential
for numerous applications in statistics, machine learn-
ing, computer graphics, environmental science, etc.
In many computer graphics applications such as cre-
ating bounding volume hierarchies, performing colli-
sion detection, etc. being able to find the MEB of a
set of triangle vertices is also a critical part of many
algorithms.
Formally, given c ∈ R
d
and r ∈ R, let B(c,r) de-
note the ball of points in R
d
with a Euclidean distance
of at most r from c, i.e., {x ∈ R
d
:
k
x − c
k
≤ r}. We
say that a finite set of points P = {p
0
, p
1
,..., p
n−1
} ⊂
R
d
is enclosed by B(c, r) if
p
j
− c
≤ r holds for
all j = 0,1, .. ., n−1. The MEB, which we denote by
MEB(P), is the unique ball with minimum radius that
encloses P.
It is well-known that MEB(P) is defined by at
most d +1 points from P that coincide with its bound-
ary. This makes the MEB problem a combinatorial
optimization problem, and a number of algorithms
based on locating these support points have been pre-
sented (Welzl, 1991; G
¨
artner, 1999; Fischer et al.,
2003). In high dimensions, it is often more practical
to settle for approximate solutions. Based on the pop-
ular concept of core-sets (B
˘
adoiu et al., 2002), several
strategies to obtain approximations with guaranteed
error bounds have been devised (Kumar et al., 2003;
B
˘
adoiu and Clarkson, 2008; Yıldırım, 2008; Larsson
and K
¨
allberg, 2013).
Currently there exist a number of methods that
utilize the well-known streaming model to com-
pute approximate MEBs for massive quantities of
data (Zarrabi-Zadeh and Chan, 2006; Agarwal and
Sharathkumar, 2010; Chan and Pathak, 2014). In this
paper, we instead turn to an external memory model,
which allows more than one pass over the data and en-
ables computing the exact MEB with limited space (at
the price of more I/Os). In addition, for our intended
applications, an external memory model is more ap-
propriate. Our primary focus is the three-dimensional
case, although the presented techniques are valid also
in general dimensions.
The algorithm presented here works by reading in
chunks of point data from disk and running any ap-
plicable MEB algorithm on these points in internal
memory, while maintaining the set of support points
found so far. It continues chunk by chunk until all
points are guaranteed to be contained in the computed
ball. We test variations of this to improve the practi-
cal performance of the algorithm by storing additional
information about each chunk of point data on disk.
Källberg, L., Shellshear, E. and Larsson, T.
An External Memory Algorithm for the Minimum Enclosing Ball Problem.
DOI: 10.5220/0005675600810088
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 83-90
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
83

We show that by using this extra information, we can
further reduce the number of I/O operations for an ad-
ditional doubling of performance. In fact, on several
massive input examples, our algorithm achieves simi-
lar performance using only a few megabytes of mem-
ory, as a standard MEB solver running with enough
memory to fit the entire point data in-core.
The contributions of this article are 1) an exact
external memory MEB algorithm for massive point
clouds, 2) new heuristics to further reduce the I/O traf-
fic in said algorithm, and 3) an empirical verification
of the quality of the algorithm, focusing on massive
three-dimensional point clouds.
2 RELATED WORK
The MEB problem is well-studied in computational
geometry. The problem goes back at least to the 19th
century, when English mathematician James Joseph
Sylvester posed it for points in the plane. Since
then there has been a significant amount of work on
the general d-dimensional problem; summaries are
given in, e.g., (Nielsen and Nock, 2009; Larsson and
K
¨
allberg, 2013). However, while many other prob-
lems from computational geometry have been stud-
ied in the external memory setting (Breimann and
Vahrenhold, 2003), no such studies of the MEB prob-
lem appear to exist.
For MEB algorithms not based merely on internal
memory, the focus so far has been on streaming ver-
sions of approximate MEB algorithms. In the stream-
ing model, algorithms are typically allowed only one
pass over the input data and have limited storage (of-
ten polylogarithmic). The purpose of these restric-
tions is to model, for example, the arrival of points
one at a time over a network connection. Zarrabi-
Zadeh and Chan (2006) give a streaming algorithm
that requires only O(d) memory and computes a 3/2-
approximation of the MEB in O(d) time per point in
the stream. Agarwal and Sharathkumar (2010) give
an algorithm that uses O(d/ε
3
log(1/ε)) space and
computes a (1.22 + ε)-approximate MEB (this bound
was given subsequently by Chan and Pathak (2014)).
The worst-case time complexity of this algorithm is
O(d/ε
5
) time per point. However, a practical evalua-
tion of these algorithms is still lacking.
To compute exact MEBs in low dimensions,
which is the focus of this paper, one of the best known
algorithms with a high practical value is the Miniball
algorithm by Welzl (1991). It relies on randomiza-
tion to achieve expected O(n) running times in fixed
dimension d. A na
¨
ıve out-of-core adaptation of this
algorithm, however, would likely exhibit poor I/O be-
havior due to its recursive nature and frequent revis-
iting of points in an unpredictable manner. G
¨
artner’s
variation of Miniball makes use of a pivoting heuristic
to improve the performance as well as the numerical
robustness of the algorithm (G
¨
artner, 1999). It works
by maintaining a candidate set of support points as
well as the exact MEB of these points. In each pivot
step, the farthest point lying outside of the current
MEB is found, and then this point is appended to the
support set and the MEB of the new support set is up-
dated using Welzl’s algorithm as a subroutine. This
typically causes one or more of the previous support
points to be removed, since the true support set can
have at most d + 1 points. The algorithm terminates
when no more outliers exist, which means that the
current support set and MEB constitute the final so-
lution. Contrary to the original algorithm, this algo-
rithm exhibits highly predictable and regular access
patterns in the point data and therefore makes a better
candidate for external memory operation. However, it
may still require many passes over all input points.
3 EXTERNAL MEMORY
ALGORITHM FOR MEB
3.1 I/O Memory Model
Our I/O model follows the well-known one presented
in (Aggarwal et al., 1988). In this model, any consec-
utive set of B records can be loaded from or stored to
external memory in one I/O, while the internal mem-
ory can hold up to M records at a time, where M is
a multiple of B. Other recently developed I/O models
include the unit-cost flash model presented in (Ajwani
et al., 2009), although the main characteristics of even
such more modern models are still captured well by
the aforementioned model (one needs to reinterpret
the meaning of B, etc.). Hence, we use that simple
and general model here. Compared to the streaming
model, this I/O model avoids limitations caused by al-
lowing only a single pass over the data and enables us
to compute an exact MEB using limited memory.
3.2 The Algorithm
Our algorithm is listed in Algorithm 1. It is optimized
to compute the MEB for points stored on the hard disk
and not in RAM. For example, we avoid the copying
and moving of points on the hard disk. On Line 1, the
input set is conceptually partitioned into K = dn/Be
blocks on disk, each containing B input points (ex-
cept the block H
K−1
, which stores fewer points if n is
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
84

not a multiple of B). As discussed previously, it is as-
sumed that each such block can be loaded in one I/O
transaction. On Line 2, an internal memory buffer A
with space for M points, or M/B blocks, is defined.
Of course, we assume that M < n in general, which
means that A can contain only parts of the input set at
any given time. On Line 3, a candidate solution, con-
sisting of a center point c ∈ R
d
, a radius r ∈ R, and
a support set S ⊆ P, is initialized. Similar to A, these
components are kept in-core, at an additional O(d
2
)
memory cost (as there are up to d + 1 support points).
The main loop begins on Line 6. The index i gives
the next block to be fetched from disk, and is up-
dated in a cyclic fashion as i = 0, 1,. .. ,K−1,0, 1,. ..
This means that the next block H
i
is always the block
that has been left out for the longest period of time.
The variable m counts the number of chunks that are
currently guaranteed to be enclosed in the candidate
ball B(c,r). Thus, once m = K, the loop terminates
with the final MEB. Specifically, the loop maintains
the invariant that the m chunks preceding H
i
, that is,
the chunks H
` mod K
for i − m ≤ ` < i, are enclosed in
B(c,r) (here the Euclidean, or “wrapping”, definition
of mod is used). Conversely, any other blocks must
be visited at least once more by the algorithm.
On Lines 7–14, up to M/B new blocks are fetched
from disk and inserted into the buffer A. Meanwhile,
m is speculatively incremented for each block. Then
Algorithm 1: Our exact out-of-core MEB algorithm.
Input: P = {p
0
, p
1
,..., p
n−1
} ⊂ R
d
Output: MEB(P)
1: {H
0
,H
1
,...,H
K−1
} ← P, where K = dn/Be
2: A ←
/
0 (A is internal memory of size M)
3: c,r, S ← (0,0, .. ., 0),−1,
/
0
4: m ← 0
5: i ← 0
6: while m < K do
7: m
0
← m
8: j ← 0
9: while j < M/B and m < K do
10: A ← A ∪ H
i
11: j ← j + 1
12: m ← m + 1
13: i ← (i + 1) mod K
14: end while
15: if A 6⊂ B(c,r) then
16: c,r,S ← INCOREMEB(A ∪ S)
17: m ← m − m
0
18: end if
19: A ←
/
0
20: end while
21: return B(c,r)
on Lines 15–18, it is first checked whether the newly
fetched blocks are enclosed in the current ball. If so,
the algorithm simply continues. Otherwise, the solu-
tion is updated by calling an auxiliary MEB solver in-
core on A as well as the current set of support points
S. Note that this always causes the radius r to grow,
since the new ball encloses the support points of the
previous ball as well as at least one point in A that is
outside of it. Despite this, however, any blocks that
were known to be enclosed by the previous ball are
not guaranteed to be enclosed by the new ball. There-
fore m must be decremented by its previous value,
which is saved in m
0
, to mark that only the blocks in
A are currently known to be enclosed in the ball.
3.3 Filtering Heuristics
To further lower the number of I/O operations and im-
prove performance, we now introduce filtering heuris-
tics that can be easily incorporated into Algorithm 1
with little additional processing cost. These heuristics
are based on skipping over blocks in the inner loop on
Lines 9–14 if they are already enclosed in the cur-
rent ball. In other words, if the condition H
i
⊂ B(c, r)
holds, the block H
i
is not added to A and the index j
is not incremented. Of course, this is beneficial only
if the condition can be evaluated without first having
to fetch H
i
from disk, and we describe below how this
can be accomplished. However, it is crucial to note
that this condition does not guarantee that the block
H
i
will be enclosed in the ball after the next update.
Thus, when filtering a block, m
0
must updated to the
current value of m + 1 so that the block is counted
among those that will later be subtracted from m in
case the ball needs to be updated (Line 17). This
makes sure that the invariant is maintained and that
the filtered block will be considered at least one more
time by the algorithm. However, intuitively the same
block is likely to be filtered on the next visit as well.
In general terms, first note that the condition H
i
⊂
B(c,r) holds if and only if
kq
i
− ck ≤ r,
where q
i
= argmax
p∈H
i
kp − ck, the farthest point in
H
i
from c. While the exact distance kq
i
−ck cannot be
determined without fetching H
i
from disk and finding
the point q
i
, an upper bound can be calculated using
the triangle inequality:
kq
i
− ck ≤ kc − c
0
k + kq
i
− c
0
k
≤ kc − c
0
k + kq
0
i
− c
0
k,
where c
0
denotes some selected reference point and
q
0
i
= arg max
p∈H
i
kp − c
0
k. Replacing the left-hand
side of the original condition by this upper bound
An External Memory Algorithm for the Minimum Enclosing Ball Problem
85

gives the following conservative condition, which can
be evaluated instead of the exact containment test:
kc − c
0
k + kq
0
i
− c
0
k ≤ r. (1)
By selecting c
0
and computing kq
0
i
− c
0
k for each H
i
while the block resides in memory, this condition can
be evaluated completely in-core the next time H
i
is
revisited, before loading it from disk. For clarity, a
replacement for the inner loop on Lines 9–14 in Al-
gorithm 1 that uses this general approach is shown in
Algorithm 2.
Algorithm 2: Filtering version of the inner loop.
while j < M/B and m < K do
if kc − c
0
k + kq
0
i
− c
0
k > r then
A ← A ∪ H
i
j ← j + 1
else
m
0
← m + 1
end if
m ← m + 1
i ← (i + 1) mod K
end while
Provided that H
i
⊂ B(c,r) holds for a significant
portion of the blocks, the effectiveness of the filter-
ing condition (1), in terms of skipped disk transfers,
depends on how tightly the real distance kq
i
− ck is
bounded by the left-hand side. This, in turn, depends
on the selected reference point. We consider two dif-
ferent approaches to do this selection. The first is to
compute and save MEB(H
i
) in-core when each chunk
H
i
is loaded from disk for the first time. Then, each
time chunk H
i
is revisited, the center c
∗
i
of MEB(H
i
)
is inserted as the reference point c
0
in (1) and the con-
dition is evaluated before loading the chunk H
i
. Note
that the term kq
0
i
− c
0
k of (1) is simply given by the
radius r
∗
i
of MEB(H
i
), while the left term needs to be
recomputed each time. Thus, the condition becomes
kc − c
∗
i
k + r
∗
i
≤ r. (2)
In the second approach, (1) is instead evaluated
with c
0
set to the value of c at the time each block H
i
was last loaded and processed. This means that each
time c has been updated on Line 16, an in-core copy
of the new c, call it c
i
, is stored to be employed the
next time any of the blocks currently in A are revis-
ited. Also, before evicting the blocks in A from mem-
ory on Line 19, the point q
0
i
∈ H
i
that is farthest from
c
i
is located for each block (which can be done as a
side effect of INCOREMEB on Line 16) and saved, to
provide the second term in the left-hand side of the
condition:
kc − c
i
k + kq
0
i
− c
i
k ≤ r. (3)
As with (2), the first term needs to be recomputed
with the latest value of c to evaluate the condition. As
each of the heuristics has a fairly negligible overhead,
they can also be combined for additional effects. Each
chunk is then loaded only if both of the conditions (2)
and (3) fail.
Similar filtering techniques have previously been
employed for MEB computations. In (K
¨
allberg and
Larsson, 2013), upper bounds derived using the trian-
gle inequality are used to skip superfluous distance
computations while computing (1 + ε)-approximate
MEBs in internal memory. A challenge present in this
work is that a single bound must be derived for an
entire chunk of points, as opposed to having tighter
bounds at the granularity of individual points in the
chunk. On the positive side, we can afford to use more
sophisticated strategies to select the reference point c
0
,
as the cost of doing this selection is amortized over the
loading and processing of a whole chunk.
3.4 Analysis
The memory requirements of the basic version of Al-
gorithm 1 are O(M) for fixed d. The filtering heuris-
tics, on the other hand, increase the memory require-
ments to Ω(M +n/B), because of the additional infor-
mation stored for each of the dn/Be blocks. However,
in low dimensions this additional memory should not
cause problems. For example, with d = 3, n = 10
9
,
and a chunk size of 1MB, it amounts to only about
17% of a single chunk (assuming single-precision
floating-point values are used).
Given that the exact MEB can be computed in lin-
ear time in fixed dimension, the update step in the al-
gorithm takes O(M) time per iteration. Similarly, the
remaining work per iteration takes O(M) time, with
or without filtering enabled. While the number of it-
erations might be very large in the worst case, most
inputs encountered in practice are likely to require
only a few iterations. Since a rigorous average-case
analysis is non-trivial, however, we settle for an in-
formal discussion here. First note that once all of
the at most d + 1 support points of MEB(P) are en-
closed in the candidate ball B(c,r), it must hold that
B(c,r) = MEB(P). Thus, once this occurs, the algo-
rithm will only need to check the fewer than dn/Be
remaining chunks on disk for containment in the ball.
Furthermore, between each visit of a chunk H
i
, a se-
quence of monotonically growing candidate balls is
generated, and each support point of MEB(P) is en-
closed in at least one of these balls. We propose that
“on average”, one more of the support points is en-
closed in B(c,r) after every k-th such visit, where k is
a constant. Under this assumption, the number of iter-
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
86

ations becomes O(dkn/M). For fixed dimension, the
total time complexity thus becomes O(n). Because
at most M/B chunks are loaded in each iteration, the
total number of I/O transactions becomes O(n/B).
The rationale behind the filtering heuristics is that
for reasonably uniform distributions, a large portion
of the points fall inside the ball throughout most of the
iterations. The blocks containing these points are un-
likely to contain the support points of the final MEB,
and it is therefore beneficial to postpone the loading
of such blocks as much as possible. Our first filter-
ing heuristic can be expected to work well when the
points are stored on file with a structure that matches
their spatial distribution. Given a sufficiently small
chunk size B, the radius r
∗
i
of each MEB(H
i
) then
becomes small, which facilitates the tightness of the
bound used in condition (2). For point sets that are
stored in an unstructured manner on file, on the other
hand, the term r
∗
i
might become too large in gen-
eral for condition (2) to be effective. Then the sec-
ond heuristic, using condition (3), might be a better
choice. As long as the position of the ball center has
not changed by a considerable amount since a block
H
i
was last considered, the term kc − c
i
k in condi-
tion (3) becomes small enough to give a tight bound.
4 EXPERIMENTS
We carried out experiments that focused on using
Algorithm 1, with and without the heuristics from
Section 3.3, for nonsynthetic three-dimensional point
clouds containing tens to hundreds of millions of
points. As a performance baseline, we also included a
relatively straightforward adaptation of G
¨
artner’s al-
gorithm for external memory. Although this algo-
rithm was not designed with external memory scenar-
ios in mind, we deemed it the most competitive alter-
native among the available exact algorithms. In our
adaptation, the farthest point is found in each pass by
loading the chunks one by one and scanning through
them. An obvious optimization is to always start each
pass by scanning the blocks already in memory since
the previous pass, and we incorporated this in our im-
plementation. We based this code on version 3.0 of
the publicly available C++ implementation
1
, which
was also used for the internal memory MEB solver
in our own algorithm.
The platform used for our measurements was a
laptop PC with an Intel Core i7-3820QM (2.7 GHz)
processor running Windows 7. Since this platform
has 16 GB of memory, we simulated smaller mem-
1
http://www.inf.ethz.ch/personal/gaertner/miniball.html
Figure 1: Point clouds used in the experiments: Chalmers,
Lab, Tower, David, St. Matthew, and Atlas. The image of
Tower is due to (Borrmann et al., 2011).
ory sizes in software. To ensure that all file accesses
were served directly by the hard drive, as would be
the case in a real system with limited main mem-
ory, we disabled all file caching on the operating sys-
tem level using the FILE FLAG NO BUFFERING flag
in the Windows I/O API. The hard drive used was
a Samsung PM830 mSATA solid-state drive. This
hard drive is specified as having a peak read through-
put of 500 MB/s. With overlapped I/O turned off,
we measured a peak throughput of roughly 275 MB/s
using the ATTO benchmarking tool (ATTO Technol-
ogy, Inc., 2010), and roughly 260 MB/s in our own
testing framework. These speeds were obtained us-
ing a transfer size of about 4 MB or larger. We
chose a block size B of 2
18
points, which, given that
each point takes 12 bytes, gives a transfer size of
3 MB. Although larger values of B would give slightly
faster transfers, using smaller B facilitates the filtering
heuristics, therefore we chose this compromise.
In all runs we used single-precision floating-point
arithmetic. Unfortunately, this caused the internal
MEB solver (Line 16 in Algorithm 1) to occasionally
return a ball whose radius is slightly smaller than or
equal to the previous radius, although mathematically
An External Memory Algorithm for the Minimum Enclosing Ball Problem
87
Lab
n = 100M
Tower
n = 152.2M
Chalmers
n = 534.2M
0
2
4
I/O/block
0
1
2
3
4
0
1
2
3
4
2
18
2
20
2
22
2
24
2
26
2
27
0
10
20
M
time (sec)
2
18
2
20
2
22
2
24
2
26
2
28
0
10
20
30
M
2
18
2
20
2
22
2
24
2
26
2
28
2
29
0
50
100
M
David
n = 28.2M
St. Matthew
n = 186.8M
Atlas
n = 254.8M
0
2
4
6
I/O/block
0
2
4
6
0
1
2
3
4
2
18
2
19
2
20
2
21
2
22
2
23
2
24
2
25
0
2
4
6
8
M
time (sec)
2
18
2
20
2
22
2
24
2
26
2
28
0
20
40
60
M
2
18
2
20
2
22
2
24
2
26
2
28
0
20
40
M
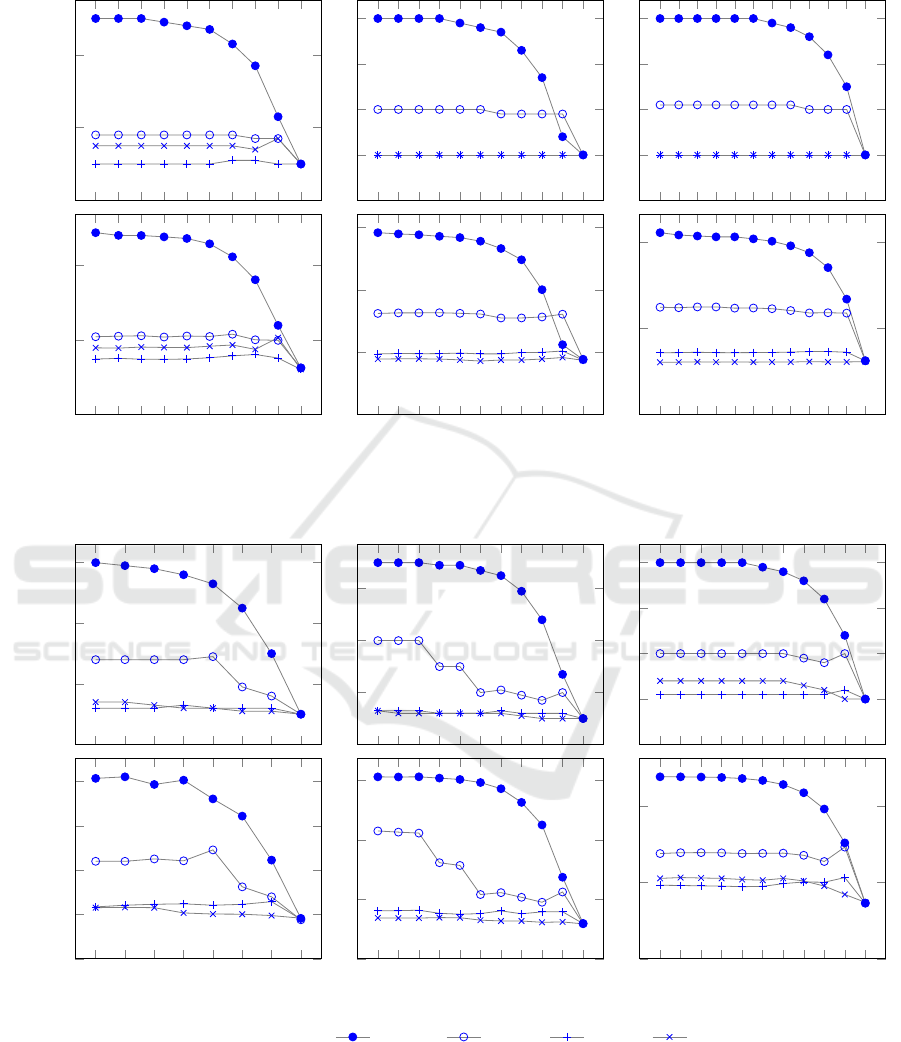
Figure 2: Results from experiments. Legend: Miniball, Algo. 1, Heur. 1, Heur. 2. The horizontal axes
show the simulated memory sizes M, measured in number of points.
it should increase monotonically. To ensure termina-
tion of Algorithm 1, we let the new radius be replaced
by the previous one if it has not increased, while the
updated center point is always kept. Also, when this
happens, it is not counted as an update and m is not
decremented. In the public implementation of Mini-
ball, the analogous problem is tackled by terminating
the algorithm as soon as such a decreased radius ap-
pears.
The point clouds we tested are shown in Fig-
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
88

ure 1. The first point cloud, Chalmers, is a scan
of the Chalmers University of Technology in Swe-
den and contains 534 million points. The next point
cloud, Lab, is a scan of the production laboratory at
the Chalmers University of Technology and contains
100 million points. Both of these scans were made
using a FARO Focus 3D 120. The Chalmers scan
was put together from 21 separate scans from differ-
ent positions, and the Lab scan was put together from
11 scans. A fly-through of the Chalmers point cloud
is available on the web
2
.
The next point cloud is the publicly available
Tower data set by Borrmann et al. (2011), which
contains 152 million points. The remaining three
point clouds were created by extracting the vertices
from triangle meshes from the Digital Michelan-
gelo Project Archive (Stanford Graphics Laboratory,
2015). These three meshes—David, St. Matthew, and
Atlas—contain 28 million, 187 million, and 255 mil-
lion vertices, respectively. Each point cloud was pre-
processed into the binary xyz format to ensure consis-
tent access times over all cases.
The results from our experiments are shown in
Figure 2. Two plots are included for each input set,
the top one showing the average number of I/O trans-
actions performed per block for different memory
sizes, and the bottom one showing the resulting ex-
ecution times. The values of M are sampled start-
ing at 2
18
= B, and then increased by a factor of 2 in
each step until M ≥ n. This means that at the lowest
value of M, only a single block fits in memory, and at
the largest value, the whole point set fits in memory
(which leads to the plots converging at an I/O/block
of 1). Each plot includes Miniball, Algorithm 1, and
Algorithm 1 incorporating heuristics 1 and 2 (based
on conditions (2) and (3) from Section 3.3, respec-
tively).
4.1 Discussion of Results
Perhaps the most important statistic to consider is
the number of I/O operations performed by the al-
gorithms, as this is independent of the type of hard
drive used. For almost any value of M our algo-
rithm reduces I/O considerably over Miniball, up to
three times without the heuristics and up to six times
with the heuristics enabled. Furthermore, by using the
heuristics we achieve close to the optimal I/O of only
one read per block across all values of M. Miniball
requires fewer I/O operations as the memory size in-
creases, because more blocks can be cached between
passes in internal memory (as discussed above). Nev-
2
https://vimeo.com/117913688
ertheless, only at M ≈ n/2 does Miniball start to ex-
hibit competitive I/O and performance.
The basic version of Algorithm 1 performs be-
tween two and four I/O operations per block, indepen-
dently of the number of points. This is in accordance
with our speculation in Section 3.4 that the number
of visits of each block is within a constant factor of
d, and ultimately that the algorithm has a linear time
complexity in n for fixed dimension.
The better I/O performance almost directly trans-
lates one-to-one into faster algorithms. For example,
in the Tower and Chalmers cases, four times better I/O
results in roughly three times better runtimes. The
largest performance gains are seen for St. Matthew,
where the fastest heuristic is up to four times faster
than the Miniball algorithm. As the two heuristics ex-
hibit similar effect on I/O in general, we can see that
the first heuristic has a slightly larger overhead than
the second one. This stems from the relatively high
cost of invoking an additional full MEB computation
for each chunk.
5 CONCLUSION
In this paper we developed an algorithm aimed at effi-
cient out-of-core MEB computations. The presented
algorithm and additional heuristics were able to re-
duce the number of I/O operations by almost an order
of magnitude over a na
¨
ıve out-of-core implementa-
tion of (G
¨
artner, 1999). For our hardware setup this
resulted in up to four times better performance. Most
importantly, this could be achieved with only a few
megabytes of internal memory, which is beneficial for
memory-limited systems such as mobile phones, em-
bedded systems, etc.
In the first version of our algorithm, only the can-
didate support set is carried over between chunks
(apart from the candidate ball, which can be computed
from the support points), and this is arguably the min-
imum amount of information necessary to compute
an exact MEB. However, one can easily imagine diffi-
cult input cases, such as point sets having many points
close to the boundary of the MEB, for which this
strategy would be insufficient and would incur many
passes over the input. It is an interesting direction
for further studies to develop more sophisticated rep-
resentations that can handle such difficult cases ef-
fectively by keeping more information about visited
chunks in a memory-efficient way. Although compact
representations have been proposed for the computa-
tion of approximate MEBs (Agarwal and Sharathku-
mar, 2010), it is not clear that these can benefit exact
MEB computations.
An External Memory Algorithm for the Minimum Enclosing Ball Problem
89

Other directions for future work include more ef-
ficient data fetching techniques, where the processing
of points in memory is overlapped with data trans-
fers from disk, and investigating higher-dimensional
cases. We have done initial experiments up to d = 10
using data sets that were randomly generated from
uniform and Gaussian distributions, with encouraging
results similar to those presented here.
ACKNOWLEDGEMENTS
The Chalmers and Lab point clouds were kindly pro-
vided by Erik Lindskog and Jonatan Berglund from
Chalmers University of Technology. The Tower data
set is courtesy of (Borrmann et al., 2011). We thank
the Stanford Computer Graphics Laboratory for pro-
viding the David, St. Matthew, and Atlas data sets.
Linus K
¨
allberg and Thomas Larsson were supported
by the Swedish Foundation for Strategic Research,
grant no. IIS11-0060. Evan Shellshear was supported
by the Swedish Governmental Agency for Innovation
Systems.
REFERENCES
Agarwal, P. K. and Sharathkumar, R. (2010). Streaming al-
gorithms for extent problems in high dimensions. In
Proceedings of the Twenty-First Annual ACM–SIAM
Symposium on Discrete Algorithms, pages 1481–
1489. Society for Industrial and Applied Mathemat-
ics.
Aggarwal, A., Vitter, J., et al. (1988). The input/output com-
plexity of sorting and related problems. Communica-
tions of the ACM, 31(9):1116–1127.
Ajwani, D., Beckmann, A., Jacob, R., Meyer, U., and
Moruz, G. (2009). On computational models for flash
memory devices. In Experimental Algorithms, pages
16–27. Springer.
ATTO Technology, Inc. (2010). ATTO Disk Benchmark
v2.47. http://www.attotech.com/disk-benchmark/.
B
˘
adoiu, M. and Clarkson, K. L. (2008). Optimal Core-Sets
for Balls. Computational Geometry, 40(1):14–22.
B
˘
adoiu, M., Har-Peled, S., and Indyk, P. (2002). Approx-
imate clustering via core-sets. In Proceedings of the
Thirty-Fourth Annual ACM Symposium on Theory of
Computing (STOC ’02), page 250.
Borrmann, D., Elseberg, J., Houshiar, H., and N
¨
uchter, A.
(2011). Tower data set. http://kos.informatik.uni-
osnabrueck.de/3Dscans/. Jacobs University Bremen.
Breimann, C. and Vahrenhold, J. (2003). External mem-
ory computational geometry revisited. In Meyer, U.,
Sanders, P., and Sibeyn, J., editors, Algorithms for
Memory Hierarchies, volume 2625 of Lecture Notes
in Computer Science, pages 110–148. Springer.
Chan, T. M. and Pathak, V. (2014). Streaming and dynamic
algorithms for minimum enclosing balls in high di-
mensions. Computational Geometry, 47(2):240–247.
Fischer, K., G
¨
artner, B., and Kutz, M. (2003). Fast
Smallest-Enclosing-Ball Computation in High Di-
mensions. In Proceedings of the 11th European Sym-
posium on Algorithms (ESA ’03), pages 630–641.
G
¨
artner, B. (1999). Fast and robust smallest enclosing
balls. In Proceedings of the 7th Annual European
Symposium on Algorithms (ESA ’99), pages 325–338.
Springer.
IDC (2014). The Digital Universe of Opportunities:
Rich Data and the Increasing Value of the Internet
of Things. http://www.emc.com/leadership/digital-
universe/2014iview/.
K
¨
allberg, L. and Larsson, T. (2013). Faster approxima-
tion of minimum enclosing balls by distance filtering
and GPU parallelization. Journal of Graphics Tools,
17(3):67–84.
Kumar, P., Mitchell, J. S. B., and Yildirim, E. A. (2003).
Approximate minimum enclosing balls in high dimen-
sions using core-sets. Journal of Experimental Algo-
rithmics, 8.
Larsson, T. and K
¨
allberg, L. (2013). Fast and robust approx-
imation of smallest enclosing balls in arbitrary dimen-
sions. Computer Graphics Forum, 32(5):93–101.
Nielsen, F. and Nock, R. (2009). Approximating smallest
enclosing balls with applications to machine learning.
International Journal of Computational Geometry &
Applications, 19(5).
Stanford Graphics Laboratory (2015). The Digi-
tal Michelangelo Project Archive of 3D Models.
http://graphics.stanford.edu/data/dmich-public/.
Welzl, E. (1991). Smallest enclosing disks (balls and ellip-
soids). New results and new trends in computer sci-
ence, 555(3075):359–370.
Yıldırım, E. A. (2008). Two algorithms for the minimum
enclosing ball problem. SIAM Journal on Optimiza-
tion, 19(3):1368–1391.
Zarrabi-Zadeh, H. and Chan, T. M. (2006). A simple
streaming algorithm for minimum enclosing balls. In
Proceedings of the 18th Annual Canadian Conference
on Computational Geometry (CCCG ’06).
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
90
