Fast Screen Space Curvature Estimation on GPU

Martin Prantl, Libor V

sa and Ivana Kolingerov

University of West Bohemia, Plzen, Czech Republic

Keywords:

Curvature, Screen Space, GPU, Visualisation, Discrete Differential Geometry, Computer Graphics.

Abstract:

Curvature is an important geometric property in computer graphics that provides information about the be-

havior of object surfaces. The exact curvature can only be calculated for a limited set of surfaces description.

Most of the time, we deal with triangles, point sets or some other discrete representation of the surface. For

those, curvature computation is problematic. Moreover, most of existing algorithms were developed for static

geometry and can be slow for interactive modeling. This paper proposes a screen space method which es-

timates the mean and Gaussian curvature at interactive rates. The algorithm uses positions and normals to

estimate the curvature from the second fundamental form matrix. Using the screen space has advantages over

the classical approach: low-poly geometry can be used and additional detail can be added with normal and

bump maps. The screen space curvature can be easily added to existing rendering pipelines. The proposed

algorithm was tested on several models and it outperforms current state-of-the-art GPU approaches.

1 INTRODUCTION

Visualization of curvature plays an important role in

computer graphics. It can help to better understand

properties of surfaces and their convex and concave

areas. In computer graphics, the basic representation

of geometry is a triangle mesh. It represents only an

approximation of the original geometry and the same

triangle mesh can be obtained for different geome-

tries. Therefore it is only possible to compute an es-

timation of the curvature of the original smooth sur-

face. For triangle meshes, curvature equals to zero

inside triangles, zero or inﬁnity on edges and inﬁn-

ity in vertices. To estimate curvature for a triangle

mesh, various algorithms were proposed, using tri-

angle neighbors and approximations to perform the

estimation. The more triangles a model has, the bet-

ter approximation can we get, but the calculation be-

comes slower. The exact curvature computation can-

not be done for volumetric data sets, height ﬁelds,

point clouds and other discrete representations either.

The curvature approximation can be computation-

ally expensive, especially if the input data are of high

quality (many triangles, high volume resolution, large

point clouds etc.). A recalculation at each frame dur-

ing interactive data changes can substantially slow the

processing down. Existing methods are mostly used

for static geometry and their real-time variants mostly

rely on parallelization using GPU.

In the proposed approach, to mitigate this prob-

lem, the curvature is not estimated directly from the

mesh, but rather from the ﬁnal rendered image in

screen space. Only the currently visible data inter-

esting for the viewer are processed. Calculations are

independent of the triangle count of the original ge-

ometry, the only limitation is the screen resolution.

The advantage is that the curvature can be calculated

from any possible model representation with the same

algorithm. There is no limitation to triangle meshes,

the ﬁnal scene can contain volumetric models, im-

plicit surfaces, procedurally generated geometry and

other screen space generated effects, such as a water

surface.

Screen space techniques can be easily added as

post-process methods or replace an existing rendering

output. Nowadays, these methods are quite popular

for many problems, such as water rendering, lighting,

ambient occlusion and reﬂections. In screen space,

however, some problems may occur, usually on object

edges, where pixel ﬂickering may appear. Another

disadvantage stems directly from the screen space it-

self, where the geometry outside the visible area can-

not contribute to the results.

The proposed screen space algorithm is designed

to be used as the ﬁrst and fast estimation of the curva-

ture. For a more precise solution, the curvature should

be approximated directly from the underlying models,

where connectivity of the triangles can be used to im-

Prantl, M., Váša, L. and Kolingerová, I.

Fast Screen Space Curvature Estimation on GPU.

DOI: 10.5220/0005676801490158

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 151-160

ISBN: 978-989-758-175-5

151

Figure 1: Tangent vectors of surface at point P.

prove the results quality.

Contributions of the proposed solution are:

• it overcomes problems with the interactivity for

a high number of triangles by approximating the

curvature directly in screen space,

• it can be used in screen space as well as in object

space with little or no modiﬁcation,

• it ﬁts directly into existing rendering pipelines and

uses only the usual outputs from deferred render-

ers (positions, normals).

The rest of this paper is organized as follows. Section

2 covers related work. Section 3 explains the pro-

posed solution in object and screen space. Section 4

presents the algorithm results. Section 5 concludes

the paper. Notation used in the article is as follows:

symbol “·” denotes the dot product, “×” denotes the

cross product, |x| is the vector length and det(X) is

the determinant of a matrix X.

2 BACKGROUND AND RELATED

WORK

2.1 Basic Theory

Only a brief introduction to curvature will be pre-

sented. For more details and proofs of theorems, we

refer the reader to (Gray, 1997).

The important surface descriptors are the funda-

mental forms. They describe the ﬁrst and second or-

der derivatives of a parameterization of the surface at

a given point of the surface.

The ﬁrst fundamental form (I) is constructed from

the ﬁrst order derivatives at a surface point, which

give us two tangent vectors (T

, T

), see Figure 1. Vec-

tors T

, T

are in general not orthogonal. They are,

however, orthogonal to the normal vector n to the sur-

face at the given point. Elements of the matrix I are

computed as



E F

F G



E = T

·T

, F = T

·T

, G = T

·T

(1)

The second fundamental form (II) is calculated

from the second partial derivatives (T

, T

) and

the normal vector (n). The elements of the matrix II

are computed as

II =



L M

M N



n =

×T

L = T

·n, M = T

·n, N = T

·n.

(2)

Combining the fundamental forms gives the shape

operator W (also known as the Weingarten operator).

For every point of the surface, it tells us the change

of the normalized normal vector in the direction of a

tangent vector at this point. W is a 2 ×2 symmetric

matrix that can be obtained from the ﬁrst (I) and sec-

ond (II) fundamental forms:

W = I

−1

II.

(3)

The matrix W has two real eigenvalues that corre-

spond to the ﬁrst (λ

) and second (λ

) principal curva-

ture, and its eigenvectors correspond to the principal

curvature directions. Mean (H) and Gaussian (K) cur-

vature are computed from principal curvatures as:

H =

(λ

+ λ

K = λ

(4)

2.2 Related Work

As already mentioned, curvature cannot be exactly

computed for discrete geometry. Instead of that, only

an approximation (or estimation) can be calculated.

There are two main categories of approaches - dis-

crete and surface ﬁtting. Discrete methods calculate

curvature directly from the data, while surface ﬁtting

tries to ﬁnd a local approximation of the surface and

calculates the curvature of this approximation. Usu-

ally, discrete methods are faster but less accurate.

There are many algorithms for the curvature esti-

mation, often varying only in details. A comparison

can be found in (Magid et al., 2007). Algorithms re-

lated to the design of the proposed algorithm are sum-

marized in the next subsections.

2.2.1 Discrete Methods

The discrete method from (Rusinkiewicz, 2004) uses

the second fundamental form to calculate the curva-

ture estimate per triangle. These curvatures are then

distributed to triangle vertices. Uniform or Voronoi

area weights can be used to express the vertex cur-

vature. This step is similar to normal vector calcu-

lation for a triangle mesh. The algorithm (Grifﬁn

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

152

et al., 2012) is used for volumetric datasets. This algo-

rithm is a variation of (Rusinkiewicz, 2004), running

entirely on GPU, and it is optimized for deformable

meshes. The interactive nature of this algorithm is

achieved by a GPU parallelization rather than algo-

rithmically.

An algorithm similar to (Rusinkiewicz, 2004) has

been presented in (Theisel et al., 2004). The triangle

curvature computation is based on triangle vertices

positions and unnormalized normals. By a linear in-

terpolation, a single point and a normal is calculated

for each triangle. The estimated curvature depends on

the length and quality of the normals.

The algorithm to compute curvature estimation di-

rectly from the triangles can be found in (Meyer et al.,

2003). The mean curvature is computed using a dis-

cretization of the Laplace operator. Voronoi areas

of triangles shared by a vertex are used as weight

functions. The Gaussian curvature is calculated from

the sum of vertex incident angles, weighted by same

Voronoi areas as for the mean curvature.

For a regular height ﬁeld, curvature can be cal-

culated directly by using Monge Patch (Gray, 1997).

From a regular height ﬁeld, derivatives can be es-

timated using neighboring points values, which are

then used in a series of equations.

2.2.2 Surface Fitting Methods

Surface ﬁtting methods approximate the surface by

the least squares techniques. An algorithm for point

clouds based on this approach was presented in (Yang

and Qian, 2007).

Surface ﬁtting can also be done by ﬁnding a local

surface approximation, often using a B

ezier patch, see

(Razdan and Bae, 2005). The curvature is computed

at a single vertex directly from the patch approxima-

tion. The computational cost is very low, but if the

selected neighborhood is small, the results can be in-

correct.

Another approach based on B

ezier patch was pre-

sented in (Zhihong et al., 2011). First, a local B

ezier

surface is calculated for every triangle. From this sur-

face, curvature can be directly calculated. The B

ezier

surface patch, however, has no G

continuity between

neighboring surfaces. On the edges, there could be a

steep change in the curvature. An improvement has

been proposed by (F

unfzig et al., 2008), where G

continuous patch is computed as a blend of B

ezier

surfaces over neighboring triangles. From this patch,

curvature can be directly calculated using an analytic

solution as proposed in (Boschiroli et al., 2012). A

drawback of this method is that the second deriva-

tives are much more complex than for a simple B

ezier

patch.

Curvature estimations based on surface ﬁtting in

screen space are not very common. The only algo-

rithm known to us is by (Mellado et al., 2013). They

propose the screen space algorithm using sphere ﬁt-

ting. For each pixel, the best ﬁtting sphere is found.

With this approach, however, only the mean curvature

is calculated, while the Gaussian and principal curva-

tures cannot be computed this way.

3 THE PROPOSED ALGORITHM

The proposed algorithm works in the screen space

and it can also be used for classic triangle meshes.

The core of the algorithm is similar to (Rusinkiewicz,

2004).

First, a description of the proposed algorithm for a

triangle mesh is presented. The screen space version

is discussed next.

3.1 BASIC ALGORITHM

The main idea is to describe every triangle indepen-

dently by the shape operator W (recall Equation (3)).

Elements of the shape operator must be calculated to

ﬁnd eigenvalues of the matrix and the ﬁnal curvatures.

The proposed method uses a local orthonormal ba-

sis. In such a case, the ﬁrst fundamental form (I) be-

comes an identity matrix, which means that the sec-

ond fundamental form (II) is equivalent to the shape

operator, i.e. W = II.

To eliminate one dimension, every triangle is

transformed to a local coordinate system, also known

as the tangent space. Once the triangle is in the local

space, one of the dimensions is constant and repre-

sents the plane of the triangle. In the following calcu-

lations, this dimension is not used and the problem is

reduced from 3D to 2D.

3.1.1 Triangle Conversion to the Local System

For every triangle, given by its vertices V

and

normal vectors V n

,V n

, a local orthonormal co-

ordinate system is built (see Figure 2).

Figure 2: Local triangle transformation.

Fast Screen Space Curvature Estimation on GPU

153

One of the triangle vertices is selected as the basis

origin and subtracted from every triangle vertex. The

matrix which transforms the triangle to the local sys-

tem is created from the three-dimensional basis vec-

tors T

, T

, n. These vectors are obtained using

−V

n =

×(V

−V

)

×(V

−V

×n

×n|

(5)

The original triangle is expressed in this local sys-

tem, resulting in vertices V

and normals

V n

,V n

. Sample conversion of one of the

triangle vertices from the global to the local system is

calculated as:









−V

) . (6)

Normals should be converted using the inverse

transposed matrix. Due to the orthonormality of the

system, the matrix inverse is not needed, since an in-

version of an orthonormal matrix is equal to matrix

transposition.

3.1.2 The Curvature Calculation

The triangle in the local space is used to build the

shape operator (see in Equation (2)), where variables

L, M, N are unknown.

The shape operator describes the change of the

normal along an edge of the triangle. The triangle is

in the local space and one of the coordinates (normal)

is constant. This coordinate is left out, which leads

to 2D vectors instead of 3D. The edges of the triangle

are expressed as 2D vectors

, v

)

= V

−V

L(i+1) mod 3

, (7)

and changes of the triangle normals are 2D vectors

(dNu

, dNv

)

= V n

−V n

L(i+1) mod 3

, (8)

where i = 1, 2, 3 is the triangle edge index.

Changes of normals along the edges of the triangle

are known. These changes together with edge direc-

tion vectors are used to create a system of equations

to ﬁnd the unknown variables L, M, N. For one edge

of the triangle, we get an underdetermined system



L M

M N







dNu

dNv



. (9)

However, by constructing the same system for ev-

ery edge of the local space triangle, an overdeter-

mined system is obtained. The system is in the form

Ax = b, the least squares method is used to obtain un-

known variables:

x =

−1

. (10)

In this particular case, the matrix A is built from

the triangle edge vectors (u

, v

)

, i = 1, 2, 3 and b

is the vector of changes of the triangle normals

(dNu

, dNv

)

, i = 1, 2, 3. Index i denotes the triangle

edge index. The ﬁnal matrices are as follows:

A =







0 u







, b =







dNu

dNv

dNu

dNv

dNu

dNv







, x =









(11)

The total number of numerical operations can be

decreased by optimization. First, a substitution B =

A is introduced. The matrix B is symmetric and its

elements can be represented by variables p, q, r:

B = A

A =





p q 0

q p + r q

0 q r





p = u

+ u

q = u

+ u

r = v

+ v

(12)

The inverse of the matrix B can be computed using

Equation (13). Since B is symmetric, the computation

is fast and easy.

−1

= det(B)





p(r + p) −q

−qr q

−qr pr −pq

−pq p(r + p) −q





(13)

The ﬁnal step is to calculate values for the un-

known vector x. A part of this step can be simpli-

ﬁed, because the inverse of the matrix B is symmetric

(see Equation (14)) and the matrix A has many zero

elements. A simpliﬁed multiplication is expressed by

Equation (15).

−1

= det(B)









(14)

−1

= det(B)∗

























(15)

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

154

Having obtained the ﬁnal vector x, we can con-

struct the desired shape operator. From this matrix,

the eigenvalues λ

, λ

are computed by solving the

characteristic polynomial. These values correspond

to the principal curvature estimated for the triangle.

These curvatures can be used to evaluate the mean and

Gaussian curvature (see Equation (4)).

The presented algorithm computes the curvature

for each triangle. To obtain the curvature at the ver-

tices, we have to use all adjacent triangles at the given

point. The ﬁnal curvature can be estimated as an av-

erage from all adjacent triangles or the curvature can

be further weighted by the triangle area.

In the above calculations, an overdetermined sys-

tem was constructed from all three edges of the trian-

gle. To solve the system, only two edges are sufﬁcient

(values for i = 3 will be zero). Differences in both ap-

proaches are discussed in Section 4.

3.2 Screen Space Version

The screen space version of the proposed algo-

rithm ﬁts directly into an existing deferred render-

ing pipeline. Only normal and depth (from which

the position is reconstructed) is required for every

pixel. There could be probably some quality improve-

ments, if additional information (id of the triangle to

which the current pixel belongs, the triangle size in

the screen space etc.) were available, but this is not

the current target.

The screen space depth buffer can be interpreted

as a 2.5D function with an underlying regular grid and

function values of the depth. In the screen space, there

is a constant step size between neighboring pixels.

Those pixels are triangulated and each pixel center is

taken as a triangle vertex. One possible local triangu-

lation can be seen in Figure 3. This screen space tri-

angulation is converted to the world or camera space

by reconstruction of the position and the normal for

each pixel. This creates a simple triangulated mesh

and the curvature is estimated on this mesh using the

technique described in Section 3.1.

Figure 3: 1-ring neighborhood pixels.

The algorithm from Section 3.1 can be used di-

rectly in the screen space. It can run entirely on the

GPU, using a pixel shader. The inverse matrix can

be computed very fast (Equation (13)) and only six

values have to be stored due to the matrix symmetry.

If all three edges of each triangle are used, there

is a limitation in Equation (15) caused by shaders,

where maximal dimension of the native data type can

be four, but 3 ×6 matrix and 6 ×1 vector are needed.

If the simpliﬁed matrices from Equation (15) are used,

the calculation can be split into two parts. Each of

these parts has a halved dimension (Equation (16)) of

the original matrix.





+ v

g +v









+ v





x = det(B)









dNu

dNv

dNu





+ B





dNv

dNu

dNv









(16)

If only two edges are used, calculations can be

computed even more efﬁciently on the GPU:

x = det(B)





+ v

g +v

+ v











dNu

dNv

dNu

dNv







(17)

All calculations are based on triangles that need

to be reconstructed in the screen space. They are ob-

tained directly from the currently rendered pixel and

its neighbors, see again Figure 3. However, if the

neighborhood width is only one pixel (as in Figure

3), according to our tests, a single triangle sufﬁces to

compute the curvature estimation.

3.3 Level of Detail

In the screen space, visible details often depend on the

camera distance from the scene. Small triangles in the

world space may occupy almost all the pixels of the

rendered image if the camera is very close to the sur-

face. If the camera is far away, the same triangle can

take only one pixel of the ﬁnal image. Considering

this, a level of detail technique can be used to improve

the visual quality of the estimated curvature.

If only a basic 1-ring neighborhood is used (see

Figure 3), triangles of the original mesh can be seen

in the estimated curvature (see Figure 4(a)). The es-

timated curvature within every triangle is constant.

GPU interpolates normals and positions during ren-

dering, leading to smooth Phong shading, but the pro-

posed method uses differences in the positions and

Fast Screen Space Curvature Estimation on GPU

155

normals which are constant (except for the numeri-

cal errors) for the ﬂat geometry. It leads to constant

curvature at every pixel of each triangle.

To mitigate this problem, level of detail (LOD)

sampling can be used. For closer points, triangles

are constructed from a wider neighborhood. Using

this approach, the curvature should be computed from

more than one triangle. A maximal number of eight

triangles per pixel, creating a triangle fan, is sufﬁcient

according to our experiments. The ﬁnal curvature is

calculated as an average value from all triangles. The

result with LOD is shown in Figure 4(b).

(a) Without LOD (b) With LOD

Figure 4: Screen space curvature.

3.4 Limitations

Similarly to other screen space techniques, the pro-

posed algorithm has its disadvantages. When two

neighboring pixels do not come from the same part

of the surface, there appears a surface discontinuity

between those pixels and an artifact in the computed

curvature may appear.

If only 1-ring neighborhood is used, this problem

is not signiﬁcant and can be sometimes ignored. It

causes incorrect curvature on edges, but those incor-

rect values are only one pixel wide.

Incorrect values are more problematic when LOD

is used. The reconstructed triangles may consist of

points, which come from a discontinuous surface.

This situation cannot be distinguished directly in the

screen space. To solve this problem, conditions based

on the depth can be used. If the depth value of a

screen space triangle is bigger than a threshold, the

triangle is rejected and not used in further computa-

tions. If all triangles are rejected, we use only one tri-

angle without LOD to estimate the curvature for the

current pixel. This approach is not optimal and in the

future, we would like to improve it in the future by

using a different triangle reconstruction technique or

by detecting problematic cases more accurately than

by a threshold.

4 EXPERIMENTS AND RESULTS

To test the proposed method, a PC with the following

conﬁguration was used: Intel Core i7 CPU running

at 4GHz, 32GB of RAM memory, nVidia Geforce

960GTX graphics card with 2GB of video memory.

The algorithm was implemented in C++ and OpenGL

4.4 with GLSL shaders.

The implementation of the algorithm by (Mellado,

2015), based on (Mellado et al., 2013), was done us-

ing GLSL instead of CUDA used in the original paper.

The color gradient used for all visualisations goes

from a blue for negative values to a red color for pos-

itive values. A green color in the middle represents

zero. See Figure 5.

Figure 5: Color gradient used in presented visualizations.

4.1 Curvature Error

In this section, comparison of the proposed method

for a triangle mesh, as deﬁned in Section 3.1, and

exactly computed curvature from analytic surfaces is

provided. Every test uses exact unit-length normals

computed from the function itself. In the compar-

isons, two and three edges were used to create the

overdetermined system of equations.

The proposed method on the triangle mesh has

been also tested against the B

ezier triangles algorithm

from (Zhihong et al., 2011).

First, a sphere was tested. A sphere has a con-

stant mean and Gaussian curvature, dependent on the

sphere radius r. Curvatures on the sphere can be cal-

culated as H =

and K = −

. As a discrete repre-

sentation of the sphere, a subdivided icosahedron with

an exact normals and radius 6 was used. The pro-

posed method in both variations has a constant mean

squared error (MSE) with value 8.2 ∗10

−16

for Gaus-

sian and 7.8 ∗10

−17

for mean curvature. For different

radii, MSE has a similar behavior.

Next, two analytic functions were tested (see Fig-

ure 6). The function f

has convex and concave parts,

a high peak at its center, and it is undeﬁned at the point

[0, 0] (at this point, division by zero would occur).

Function f

has a saddle shape with minor bumps.

For tests, the functions were tessellated using a

Delaunay triangulation in the XY plane using uni-

formly distributed points with x, y ∈ [−10, 10]. The

MSE value gives the error of the proposed method on

the triangle mesh in comparison with the curvature

analytically computed from the input function. See

Figure 7.

Results of the comparison are in Figure 8. Small

peaks in the graph are caused by randomness of the

point positions. It is more visible for f

due to its

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

156

Figure 6: Tested functions f

= 10

sin(

√

)

√

)

, (x 6= 0), (y 6=

0), f

= sin(x)cos(y) +0.1(x

−y

), x, y ∈< −10;10 >.

(a) Mean curvature (b) Gaussian curvature

Figure 7: Curvatures of f

calculated from the triangle

mesh.

peak around the point [0, 0]. For denser tesellations,

there is a small difference in using two or three edges

of the triangle to solve the system. In some cases, two

edges offer better results and vice versa.

Another comparison of the proposed method was

done against the algorithm (Zhihong et al., 2011) us-

ing B

ezier triangles. This algorithm was chosen ac-

cording to the promising results published in the orig-

inal paper. The algorithm has worse results on the tri-

angle meshes created using random points, see Figure

9. The MSE values were varying from 0.5 to almost

Figure 8: MSE of the method for the triangle mesh com-

pared to the analytically computed curvature evaluated di-

rectly from the implicit function.

(a) (Zhihong et al.,

2011)

(b) Proposed method

Figure 9: The comparison of the curvature of f

, compared

on a tessellation created on random points.

40. For most of the triangles, the calculated curvature

gives the error comparable with our proposed method,

however, large error values appeared for some small

or sliver triangles resulting in too arched B

ezier tri-

angles. This problem is not present in the proposed

method.

4.2 Screen Space Comparison

The comparison of the screen space method is done

against the curvature calculated by the proposed

method using three edges directly on the triangle

mesh with and without the LOD active. Even with

only two edges, the results were almost identical

(about 2% difference in calculated values). The pro-

posed algorithm was also compared with (Mellado

et al., 2013), the only other screen space technique

known to us.

The tested models are: Stanford Dragon (300 000

vertices), MaxPlanck (152 403 vertices), Function f

(15 000 vertices) and Subdivided icosahedron (vary-

ing number of vertices). In the screen space, the qual-

ity of the computed curvature depends on the camera

distance from the model. If we compute the curva-

ture for the triangle mesh and render the result, with

the camera moving away from the model, the trian-

gles become smaller and more triangles can be ren-

dered in the same pixel. This can cause an incorrect

curvature to be visualized. In the proposed screen

space method, the problem associated with rasteriza-

tion cannot happen, because only the visible parts are

used to calculate the result and only one value is used

for the ﬁnal pixel. In every test, the model was tested

as fully visible on the screen and the camera was mov-

ing away from the model. The dependency of MSE

on the distance between the viewer and the model is

shown in the following graphs.

The test with recursively subdivided icosahedron

sphere with radius 6 showed a similar behavior to the

per vertex computed values from tests in Section 4.1.

The only difference was a small noise between edges

of the model and the background of the scene.

Fast Screen Space Curvature Estimation on GPU

157

Figure 10: Comparison of the screen space MSE for the

mean curvature calculated directly from the triangle mesh.

The proposed method with, without LOD and algorithm

from (Mellado et al., 2013) (Mellado) were tested.

In all other tests, remaining models were used.

From the graphs in Figure 10 it can be seen that the

quality of both screen space algorithms is comparable

for the mean curvature. For the dragon model, using

LOD has a little or no effect at all. The original model

has a dense tessellation and LOD can skip ﬁne details.

On the other hand, for the model of the function, the

proposed method with LOD achieves better quality.

Gaussian curvature comparison was done only

with and without LOD, since there is no other screen

space method known to us that calculates the Gaus-

sian curvature. See results in Figure 11. The behav-

ior is similar to Figure 10, with a roughly doubled

amount of the MSE error. This is caused by the cur-

vature calculation, where the mean curvature is only

a sum of the principal ones, while the Gaussian is

computed by multiplying principal curvatures. In that

case, the errors of both values are multiplied as well.

The visual comparison of the proposed method

with (Mellado et al., 2013) can be seen in Figure

12. Both algorithms have a comparable visual quality.

The proposed method results look sharper, (Mellado

et al., 2013) is more blurry. See Figure 13 for com-

parison of the quality of the proposed method in the

screen space against the same method in the object

space.

No LOD is used to show real differences based on

the camera distance. For the camera at a greater dis-

tance (full model), there is almost no visible differ-

ence. With camera closer to the surface (the detailed

model), the triangles of the mesh begin to appear in

the screen space curvature.

The effect of LOD can be seen in Figures 14 - 16.

Figure 11: Comparison of the proposed screen space MSE

for the Gaussian curvature calculated directly from the tri-

angle mesh.

(a) Proposed method

(b) (Mellado et al., 2013)

Figure 12: Comparison of the mean curvature. As (Mellado

et al., 2013) has no LOD, the presented comparison also

uses none.

If the camera is moving away from the mesh, there

is a distance, from which further there is a small or

no difference between using and not using LOD. In

some cases, using LOD can bring worse results as it

smooths out ﬁne details (see Figure 14). On the other

hand, in the example of the Gaussian curvature in Fig-

ure 15, the use of LOD improved the result consider-

(a) Object space (b) Screen space without

LOD

Figure 13: Comparison of the mean curvature for the Max-

Planck model.

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

158

(a) Object space (b) Screen space without LOD (c) Screen space with LOD

Figure 14: Comparison of the mean curvature.

(a) Object space (b) Screen space without LOD (c) Screen space with LOD

Figure 15: Comparison of Gaussian curvature using function f

from Section 4.1.

(a) Object space (b) Screen space

without LOD

with LOD

Figure 16: Detail of the mean curvature.

ably. Another comparison can be seen in the closeup

in Figure 16. If the camera moves very close to the

surface, LOD is required to obtain a smooth result.

Without LOD, the computed curvature appears as ran-

dom colors. In some cases, e.g., in wireframe view,

this visualization can be sometimes enough to see the

shape. To set a suitable distance for LOD is, however,

difﬁcult - the same value does not work for all models.

4.3 Performance

The proposed method runs at interactive frame rates.

Due to the independence on the geometry, all tested

models brought nearly the same results. In the tests,

the method was computed for pixel coverage of 2 −

100 per cent of the screen. The depth value of the

remaining pixels was set to inﬁnity to discard these

pixels. The comparison was done against the screen

space method from (Mellado et al., 2013).

The resulting performance can be seen in Fig-

ures 17 and 18. In both tests, a decrease of perfor-

Figure 17: Frame time based on screen pixel coverage. The

proposed algorithm in version with only two edges (with

and without LOD) against (Mellado et al., 2013) (Mellado)

were tested.

mance is partially caused by LOD computation itself

but mostly by the need of branches in the pixel shader

to decide if the triangle can be used or will be rejected

as described in Section 3.3. With a comparable visual

quality as (Mellado et al., 2013) (no LOD used), the

proposed algorithm is much faster if calculations use

only two edges of the triangle.

In Figure 18, the same scene was tested with all

three edges used for computation. This version is con-

siderably slower, due to the solution of Equation (16).

In the two edge solution, only one matrix is needed

(Equation (17)).

Fast Screen Space Curvature Estimation on GPU

159

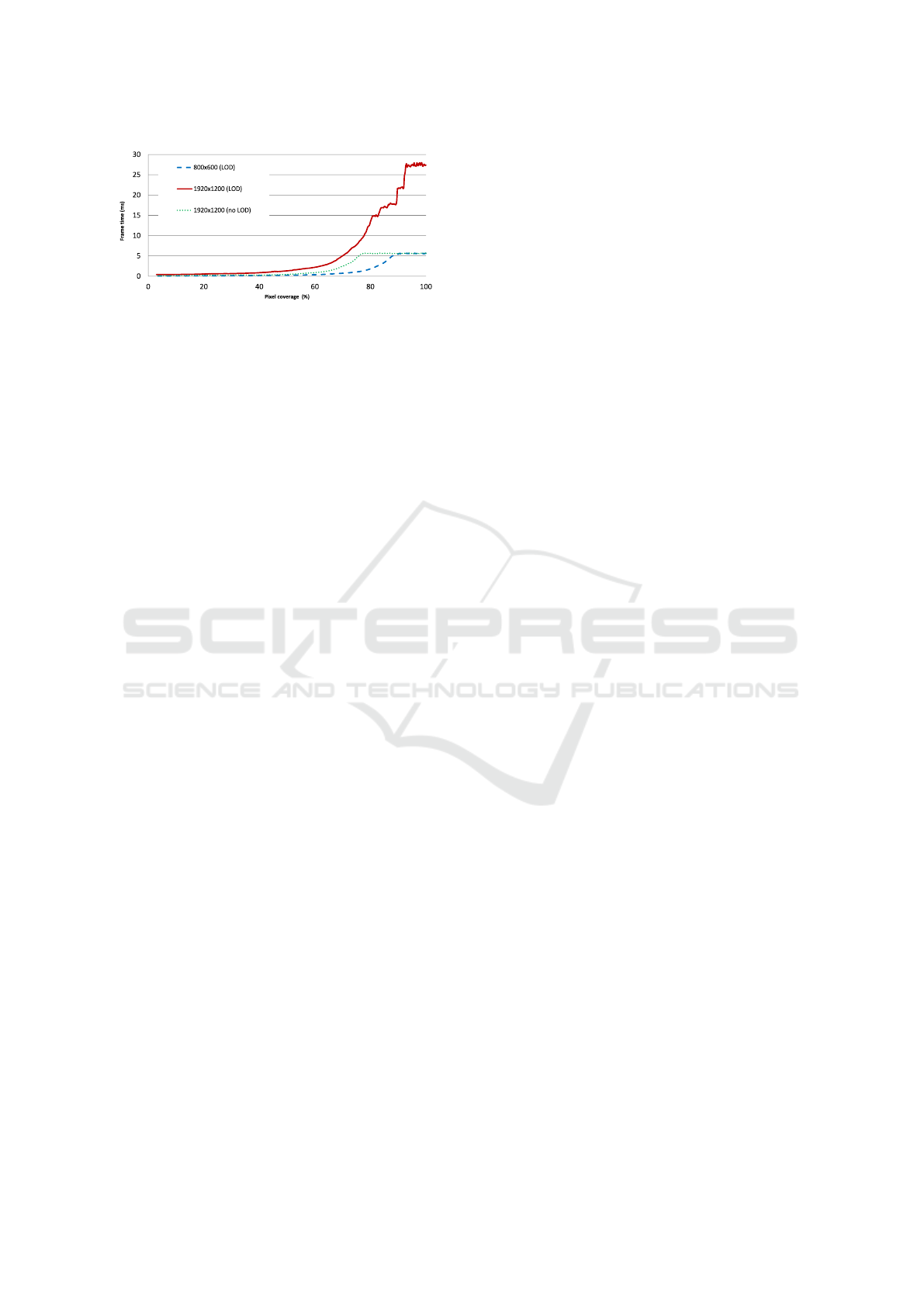
Figure 18: Proposed algorithm tested with all 3 edges of the

triangle used for the curvature calculation.

5 CONCLUSIONS

This paper presented an algorithm for estimating cur-

vature in screen space which can compute principal

curvatures, is easy to implement and runs in real-time.

It can be easily added to existing rendering pipelines.

Apart from the screen space, the same algorithm can

be used to compute the curvature directly from the tri-

angle meshes.

The limitations of this technique are similar to

other screen-space algorithms. There are possible

problems with surface discontinuities. Estimated cur-

vature depends on the distance of the mesh from the

camera, where small details are smoothed if camera

is far away from the surface.

In the future work, further LOD improvement and

stability during view changes are planned.

We would also like to use the algorithm for the

ambient occlusion estimation. Some research has

been done on this topic by (Hattori et al., 2011), but

the curvature was precalculated from the model in ob-

ject space.

A reference implementation of the proposed

method (shader source code and test application) is

available at http://graphics.zcu.cz/ sscurvature.html.

ACKNOWLEDGEMENTS

This work was supported by the Czech Ministry of

Education, Youth and Sports - the project LO1506 and

University spec. research - 1311; and by the UWB

grant SGS-2013-029 Advanced Computer and Infor-

mation Systems.

REFERENCES

Boschiroli, M., F

unfzig, C., Romani, L., and Albrecht, G.

(2012). {G1} rational blend interpolatory schemes: A

comparative study. Graphical Models, 74(1):29 – 49.

unfzig, C., M

uller, K., Hansford, D., and Farin, G. (2008).

Png1 triangles for tangent plane continuous surfaces

on the gpu. In Proceedings of Graphics Interface

2008, GI ’08, pages 219–226, Toronto, Ont., Canada,

Canada. Canadian Information Processing Society.

Gray, A. (1997). Surfaces in 3-dimensional space via math-

ematica. In Modern Differential Geometry of Curves

and Surfaces with Mathematica, chapter 17, pages

394–401. CRC Press, Inc., Boca Raton, FL, USA, 2nd

edition.

Grifﬁn, W., Wang, Y., Berrios, D., and Olano, M. (2012).

Real-time gpu surface curvature estimation on de-

forming meshes and volumetric data sets. IEEE

TVCG, 18(10):1603–1613.

Hattori, T., Kubo, H., and Morishima, S. (2011). Real time

ambient occlusion by curvature dependent occlusion

function. In SIGGRAPH Asia 2011 Posters, SA ’11,

pages 48:1–48:1, New York, NY, USA. ACM.

Magid, E., Soldea, O., and Rivlin, E. (2007). A comparison

of gaussian and mean curvature estimation methods

on triangular meshes of range image data. Computer

Vision and Image Understanding, 107(3):139 – 159.

Mellado, N. (2015). Screen space curvature using cuda/c++

(algorithm implementation from patate library).

Mellado, N., Barla, P., Guennebaud, G., Reuter, P., and

Duquesne, G. (2013). Screen-space curvature for

production-quality rendering and compositing. In

ACM SIGGRAPH 2013 Talks, SIGGRAPH ’13, pages

42:1–42:1, New York, NY, USA. ACM.

Meyer, M., Desbrun, M., Schr

oder, P., and Barr, A. (2003).

Discrete differential-geometry operators for triangu-

lated 2-manifolds. In Hege, H.-C. and Polthier, K., ed-

itors, Visualization and Mathematics III, Mathematics

and Visualization, pages 35–57. Springer Berlin Hei-

delberg.

Razdan, A. and Bae, M. (2005). Curvature estimation

scheme for triangle meshes using biquadratic bzier

patches. CAD, 37(14):1481 – 1491.

Rusinkiewicz, S. (2004). Estimating curvatures and their

derivatives on triangle meshes. In Proceedings of

the 3DPVT ’04, 2Nd International Symposium, pages

486–493, Washington, DC, USA. IEEE Computer So-

ciety.

Theisel, H., Rossi, C., Zayer, R., and Seidel, H.-P. (2004).

Normal based estimation of the curvature tensor for

triangular meshes. In CG&A, 2004. PG 2004. Pro-

ceedings. 12th Paciﬁc Conference on, pages 288–297.

Yang, P. and Qian, X. (2007). Direct computing of sur-

face curvatures for point-set surfaces. In Botsch, M.,

Pajarola, R., Chen, B., and Zwicker, M., editors, Eu-

rographics Symposium on Point-Based Graphics. The

Eurographics Association.

Zhihong, M., Guo, C., Yanzhao, M., and Lee, K. (2011).

Curvature estimation for meshes based on vertex nor-

mal triangles. CAD, 43(12):1561 – 1566.

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

160