
Efficient Culling Techniques for Interactive Deformable NURBS
Surfaces on GPU
Raquel Concheiro
1
, Margarita Amor
1
, Emilio J. Padr
´
on
1
and Michael Doggett
2
1
Computer Architecture Group, Universidade da Coru
˜
na, A Coru
˜
na, Spain
2
Lund University Graphics Group, Lund University, Lund, Sweden
Keywords:
NURBS, Real-time and Interactive Methods, Culling Techniques, Deformable Surfaces.
Abstract:
NURBS (Non-uniform rational B-splines) surfaces are the standard freeform representation in Computer-
Aided Design (CAD) applications. Rendering NURBS surfaces accurately while they are interactively manip-
ulated and deformed is a challenging task. In order to achieve it, the elimination from pipeline in early stages
of back-facing surfaces or surface pieces is a key advantage. Furthermore, an effective interactive manipula-
tion implies that all the culling computations should be performed for each frame, facing the possibility of fast
changes in occlusion information. In this paper, different interactive culling strategies for NURBS surfaces
are presented and analyzed. These culling techniques are based on the exploitation of the geometric properties
presented in a NURBS surface, that allow easily to find bounds for it in screen space for each frame. Further-
more, the culling overhead for our proposals is small compared to the computational saving, outperforming a
proposal without culling. An implementation of these strategies using current GPUs is presented, achieving
real-time and interactive rendering rates of complex parametric models.
1 INTRODUCTION
NURBS (Non-uniform rational B-splines) surfaces
(Piegl and Tiller, 1997) are widely employed in
CAD/CAM tools and graphics applications since their
essential features and qualities makes them an opti-
mal solution for modeling complex geometries. Even
though modern GPUs have introduced dedicated
hardware tessellation units (Sch
¨
afer et al., 2014),
these units do not always guarantee to have enough
tessellation level or flexibility to render a NURBS sur-
face with no artifacts, such as cracks, holes or creases.
Furthermore, NURBS surfaces introduce consider-
able advantages to the on-the-fly shape manipulation
of highly detailed geometry, as only a few patch con-
trol points (Smith and Schaefer, 2015) need to be han-
dled (see Figure 1). Clearly, adaptive rendering meth-
ods to avoid the rendering of hidden surfaces or pieces
of surfaces are key for performance. Thus, imple-
menting effective and efficient culling techniques in
the rendering pipeline is definitely important.
Traditionally, there have been two main ap-
proaches to render NURBS surfaces on GPU. The
first alternative is based on the conversion on CPU
of NURBS surfaces to other representations, such
as Catmull-Clark subdivision surfaces (Shen et al.,
Figure 1: Shape manipulation of a NURBS surface
(Killeroo Model) by interactively moving a few control
points.
2014) or B
´
ezier patches (Cohen et al., 1980), that can
be efficiently rendered on GPU (Guthe et al., 2005;
Concheiro et al., 2010; Yeo et al., 2012; Claux et al.,
Concheiro, R., Amor, M., Padrón, E. and Doggett, M.
Efficient Culling Techniques for Interactive Deformable NURBS Surfaces on GPU.
DOI: 10.5220/0005677200150025
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 17-27
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

2014; Nießner et al., 2012). The main disadvantage of
these proposals is that they can not handle deforming
NURBS surfaces interactively, since costly NURBS
surface to other representation conversions should be
performed multiple times per frame as the surface is
being deformed.
The other approach is based on rendering the
NURBS surfaces directly on GPU, with no previ-
ous conversion (Krishnamurthy et al., 2007; Krishna-
murthy et al., 2009; Concheiro et al., 2014). In (Kr-
ishnamurthy et al., 2007) and (Krishnamurthy et al.,
2009), a previous tessellation is performed on the
CPU, that creates a set of grids indicating the surface
evaluation points for different levels of detail, and
these data are sent to the GPU and stored as textures.
In (Concheiro et al., 2014), a solution for the direct
rendering of NURBS surfaces on the GPU without
any previous decomposition or tessellation to B
´
ezier
surfaces is presented. This proposal, called RPNS
(Rendering Pipeline for NURBS Surfaces) is based on
a primitive, KSQuad, which uses a regular and flexi-
ble processing of NURBS surfaces, while maintaining
their main geometric properties to achieve real-time
rendering.
Culling is the process of removing those portions
of the scene that do not contribute to the final render-
ing. The advantage of culling in the early stages of
the rendering pipeline is that entire objects that are
invisible can be removed, saving a great deal of com-
putation in the rest of the pipeline. When dealing
with polygons, one of the most traditional and stan-
dard culling techniques is Backface culling (Akenine-
M
¨
oller et al., 2008), based on removing those poly-
gons which are invisible from the viewpoint as early
as possible.
Backpatch culling (Kumar et al., 1996) is an ex-
tension of backface culling to parametric surfaces,
based on removing these invisible patches as early as
possible. Although backpatch culling is not a novel
idea, up to now it has only been applied to B
´
ezier
patches. There are basically two different groups of
proposals to compute backpatch culling: based on the
popular cone-of-normals approach (Munkberg et al.,
2010; Sederberg and Meyers, 1988; Shirman and
Abi-Ezzi, 1993) and based on the use of bounding
boxes (Kumar et al., 1996; Loop et al., 2011). In
the first group, (Sederberg and Meyers, 1988) pro-
poses a cone-of-normals derived from tangent and bi-
tangent patches, whose main drawback is the coarse
bounds that are obtained. (Shirman and Abi-Ezzi,
1993) presents a preprocessing step to compute a nor-
mal patch for a given B
´
ezier patch and to compute its
bounding cone-of-normals. Next, a simple test is used
to compute the culling on the fly. The main drawback
of this approach is that dynamic models are not ren-
dered in real time owing to the high computational
cost. (Munkberg et al., 2010) is focused on fitting this
algorithm into modern GPUs, which in turn means an
approximation in the computation of the tangent and
bi-tangent cone. With respect to the proposal based on
the computation of the bounding box of the patches,
(Kumar et al., 1996) computes the bounding box of
the normalized vectors of the normal patch, whereas
(Loop et al., 2011) constructs the B
´
ezier convex hull
of the parametric tangent plane. Instead of following
a backpatch culling approach, in (Nießner and Loop,
2012) an occlusion culling of patches is considered.
In contrast to previous alternatives, we present an
alternative solution for culling in the context of real-
time NURBS rendering with the RPNS proposal. Our
approach is based on the use of the KSQuad primitive,
and takes advantage of its strong convex hull prop-
erty. This makes it possible to support real-time an-
imated and deformed models and do not require any
pre-computed scene data structure. Furthermore, as
shown in the next sections, this culling attains an im-
portant reduction in the number of Fragment Shader
computations performed in a DirectX 11 implemen-
tation, which has a high impact on the overall perfor-
mance.
The basic concepts that support our culling pro-
posal and a brief description of RPNS are presented
in Section 2.
2 RENDERING PIPELINE FOR
NURBS SURFACES
The objective of RPNS is the efficient and accu-
rate rendering of NURBS surfaces, preventing arti-
facts in the final image such as cracks and holes,
either inside each surface or between neighbor sur-
faces. This makes it possible to exploit the paral-
lelism of the GPU to perform common operations
such as sketching on surfaces, interactive trimming
or surface-surface intersection. Figure 2 is a block
diagram of the RPNS pipeline. It consists of three
shaders: Geometry, Sampler and Rasterizer.
The input stream of the Geometry shader is a
primitive, denoted as KSQuad, that is based on the
regions defined by the projection on the parametric
cell delimited by the different knot spans. This prim-
itive provides an efficient and accurate evaluation of
NURBS surfaces in RPNS (processed in the Geome-
try stage, as shown in Figure 2). KSQuad needs no
pre-processing stage and intrinsically maintains the
main geometric properties of NURBS surfaces, such
as local support and strong convex hull. The exploita-
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
18
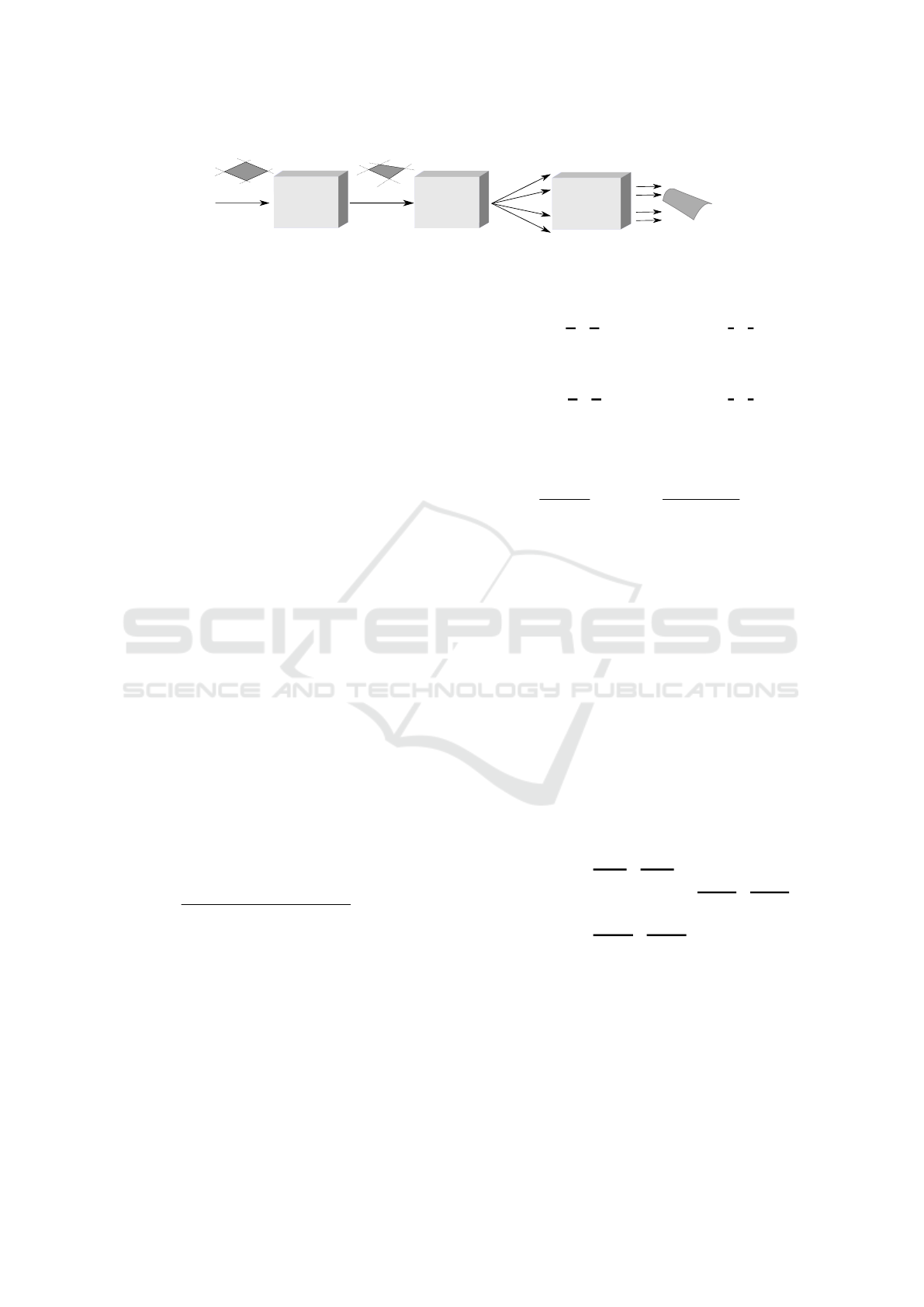
Geometry
KSQuad
Sampler
Rasterizer
.
.
.
.
.
.
KSDice
KSQuad
parametric space geometric space
Figure 2: Basic structure of RPNS’s pipeline.
tion of these properties enables us to improve perfor-
mance by applying acceleration algorithms, such as
the culling techniques described in Section 3.
In the Sampler shader, an adaptive sampling of
the KSQuad primitives is performed according to the
viewpoint, the geometric characteristics of the surface
and the boundary edges between surfaces. This sam-
pling process results in a set of sampled points or dice,
denoted as KSDice and which make it possible to ren-
der the surface without cracks or holes. Each KSDie
consists of a sampled point and additional informa-
tion such as the parametric size of the die and the
degree of the corresponding surface, and it does not
save any explicit connectivity information. Think in
KSDices as an artifact analogous to the idea of surfels
in the context of point rendering (Pfister et al., 2000).
The KSQuad discretization makes it possible to find
an optimal rendering of the geometry of surfaces with
minimum redundancy. Thus, a suitable discretization
is obtained when it can be guaranteed that there is at
least one KSDice projected into the region of each
output pixel for orthographic projection. Therefore,
the objective is to reduce the number of positions to
be evaluated for each KSQuad primitive while keep-
ing the quality of the resulting image.
A NURBS surface is obtained as the tensor prod-
uct of two NURBS curves, parametric curves that are
defined by its degree, a set of weighted control points,
and a knot vector. Thus, using two independent pa-
rameters u and v, the NURBS surface of degree (p,q),
respectively in both parametric directions, is given by
the equation:
S(u,v) =
n
∑
i=0
m
∑
j=0
N
i,p
(u) N
j,q
(v) w
i, j
B
i, j
n
∑
i=0
m
∑
j=0
N
i,p
(u) N
j,q
(v) w
i, j
, 0 ≤ u,v ≤ 1
where B
i, j
are the control points, w
i, j
are the weights,
n + 1 and m + 1 are the number of control points in
u and v parametric directions, respectively, and N
i,p
and N
j,q
are the nonrational B-spline basis function
defined on two knot vectors of r = p + n + 1 and s =
q + m + 1 elements, respectively:
U =
0,··· ,0
| {z }
p+1
,x
p+1
,··· ,x
r−p−1
,1, ···1
| {z }
p+1
V =
0,··· , 0
| {z }
q+1
,y
q+1
,··· , y
s−q−1
,1, ···1
| {z }
q+1
The basis function N
i,p
of degree p is defined for
the parametric direction u as
N
i,p
(u) =
u −x
i
x
i+p
−x
i
N
i,p−1
(u)+
x
i+p+1
−u
x
i+p+1
−x
i+1
N
i+1,p−1
(u)
(1)
with
N
i,0
(u) =
1 if x
i
≤ u < x
i+1
0 otherwise
Analogously, the basis function N
j,p
of degree q is
defined for the parametric direction v.
A NURBS surface can be seen as a grid of cells
in parametric space delimited by the different knot
spans, with each cell containing a part of the sur-
face computed with the non-zero basis functions in
that interval. Knot Span Quad (KSQuad), repre-
sents a half-open interval of the parametric domain,
[x
i
,x
i+1
)×[y
j
,y
j+1
), with non-zero length, and main-
tains the information of q ×p neighboring knot spans,
allowing an efficient evaluation of the NURBS sur-
face in this interval. So, a KSQuad
i, j
of degree q and
p is defined like
KSQuad
i, j
= {
knot span
z }| {
x
i
,x
i+1
,y
j
,y
j+1
, B
i−p, j−q
,··· , B
i, j
| {z }
control points
,
weights
z }| {
w
i−p, j−q
,··· , w
i, j
}
being x
i
6= x
i+1
and y
j
6= y
j+1
.
Each KSQuad
i, j
controls a subset of the paramet-
ric domain, defined by the rectangle parametric sub-
domain with corners (x
k
,y
l
),k ∈ {i,i + 1},l ∈ {j, j +
1}, as illustrated in Figure 3. This sub-domain is
sampled into KSDice (samples) that provide a quality
render with no holes, yet increasing the performance.
Pixel accurate rendering (Yeo et al., 2012), in RPNS
proposal is determined by the level of samples for a
Efficient Culling Techniques for Interactive Deformable NURBS Surfaces on GPU
19

Parametric Space
Model Space
(x
i
, y
j+1
)
(x
i+1
, y
j+1
)
(x
i
, y
j
)
(x
i+1
, y
j
)
S(x
i
, y
j+1
)
S(x
i+1
, y
j+1
)
S(x
i
, y
j
)
S(x
i+1
, y
j
)
Figure 3: KSQuad primitive defined by a knot interval.
given KSQuad. In screen-spacel pixel coordinates,
the samples guarantees a KSDie, by at most µ pixels:
dist(p(S(x
k
,y
k
)) − p(S(x
k+1
,y
k+1
))) < µ,
(x
i
,y
j
) ≤ (x
k
,y
k
) < (x
i+1
,y
j+1
)
(x
i
,y
j
) < (x
k+1
,y
k+1
) ≤ (x
i+1
,y
j+1
)
(2)
where p() means a screen space projection. For in-
stance, µ = 1 implies by at most half a pixel.
3 CULLING TECHNIQUES
One beneficial side effect of bringing forward the ge-
ometry stage prior to the sampling is that we can im-
prove the performance by also moving forward the
application of other techniques in the pipeline, such
as culling. Whereas backface culling is usually per-
formed after a tessellation step, we follow recent pro-
posals (Hasselgren et al., 2009) which cull before tes-
sellation to reduce as soon as possible the number of
primitives to be processed. We have called BackPatch
culling to this strategy, based on the original back-
patch idea for B
´
ezier from (Kumar et al., 1996), but
now applied to NURBS by means of the KSQUAD ar-
tifact. Two different early culling proposals based on
that idea are introduced in RPNS, performing culling
before the discretization stage.
A culling algorithm generates what is called the
potentially visible set (PVS), which is a prediction or
estimation of the exact visible set (EVS) (Akenine-
M
¨
oller et al., 2008). A PVS is conservative if it fully
includes the EVS, so that only invisible geometry is
discarded. Otherwise, a PVS is approximate when the
EVS is not fully included, which results in rendered
images with a certain error.
Our BackPatch culling strategy sends down a PVS
to the next stages in the pipeline, an approximate
set in one proposal and a conservative one in the
other. These solutions are compared to a more clas-
sic sample-based culling solution, that generates an
EVS and we have named BackDice culling, earlier
presented in (Concheiro et al., 2014).
These three culling proposals are based on differ-
ent approaches and placed in different pipeline stages
in RPNS. BackDice culling is carried out at the end
of the RPNS sampler stage (see Figure 2), once the
samples have already been obtained. On the other
hand, BackPatch culling must be placed at the begin-
ning of the geometry stage, the first step in RPNS’
pipeline (see Figure 2). Therefore, BackDice culling
works at sample level (KSDice in RPNS), whereas
the two BackPatch culling proposal do at patch level
(KSQuad in RPNS).
In any case, a previous view frustum culling is ap-
plied using the NURBS’ bounding box at KSQuad
level. This culling, based on the strong convex hull
property removes all KSQuads placed outside of the
viewing cone from being considered in the following
stages.
The strong convex hull property means a NURBS
surface is contained in the convex hull of its control
points. Moreover, if (u,v) is in the parametric rect-
angle defined by the knot spans [x
i
,x
i+1
) ×[y
j
,y
j+1
),
then S(u, v) is in the convex hull defined by the control
points {B
i−p, j−q
,. .. ,B
i, j
}.
3.1 BackDice Culling
BackDice Culling (DC) is the backface culling pro-
posal we have implemented in RPNS. It is based
on the render primitive sampled from a KSQuad:
KSDice. As traditional pipelines are triangle ori-
ented in the rendering stages, culling is usually com-
puted on triangle polygons. However, as RPNS is
based on the rendering of pieces of parametric sur-
faces, specifically KSDice, the DiceCulling proposal
removes those KSDice not turned to the camera as
early as possible.
The BackDice Culling test is placed at the end of
the sampler stage, after the screen-mapping procedure
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
20

(see Figure 2). BackDice Culling decreases the num-
ber of KSDice sent to the rasterizer, since backfaced
KSDice are culled out. However, as backface culling
computations are done in the sampler stage, in this
stage workload is slightly increased meanwhile the
rasterizer workload is reduced.
3.2 BackPatch Culling
By applying a culling technique in the first stages of
the pipeline, the number of primitives to be processed
is dramatically reduced (Hasselgren et al., 2009). To
prove this, two culling algorithms that exploit the ver-
satility and flexibility offered by the use of KSQuad
in the geometry stage have been implemented. These
culling proposals are based on the strong convex hull
property of the NURBS surfaces that is preserved in
the KSQuad primitive, and it efficiently avoids the
evaluation of points of knot spans which do not con-
tribute to the final image.
Therefore, the goal of our culling proposals is to
maintain the effectiveness of a conservative solution
with much less computation, discarding KSQuads as
early as possible in the rendering pipeline to improve
overall performance for deformable surfaces. Fig-
ure 4 shows four frames of an example NURBS sur-
face deformation. In the example, some KSQuads are
fully occluded in the initial frame but visible in the
following ones. As the results depicted in Section 5
prove, our culling proposal outperforms other alter-
natives without introducing any extra data structure,
achieving an effective and efficient interactive expe-
rience when an important deformation is applied to
high-detailed NURBS surfaces.
Unlike Dice Culling, designed to remove KS-
Dice, the two backpatch culling proposals for RPNS,
Lightweight BackPatch Culling (LQC) and Strong
BackPatch Culling (SQC), have been designed to cull
out KSQuads earlier in the pipeline. Both Back-
Patch Culling methods are based on the potentially
visible set (PVS) and independently applied to each
KSQuad, so different KSQuads of a NURBS can be
culled out, whereas other ones are rendered. Conse-
quently, KSQuads are culled before being evaluated
into KSDice. This means higher computation costs in
RPNS’ geometry stage, but reduces the workload in
the sampler and rasterizer stages.
As both techniques have been specifically de-
signed for NURBS surfaces, they are based on the
strong convex hull property previously described.
Hence, the normal to the plane defined by the skeleton
computed for each KSQuad is used instead of com-
puting the normal to the KSQuad, dramatically reduc-
ing the culling computational workload.
The proposed Light Quad Culling algorithm culls
a KSQuad
i, j
by using this simple square:
i, j
= {S(x
i
,y
j
), S(x
i+1
,y
j
), S(x
i
,y
j+1
), S(x
i+1
,y
j+1
)}
(3)
LQC is an approximate PVS technique and al-
though a fast and efficient culling computation is pro-
vided, the EVS is not fully included thus the quality
of the render is slightly decreased as will be detailed
in Section 5.
i, j
cannot guarantee that the normal of
all surface points have the same direction.
On the other hand, the SQC algorithm culls a
KSQuad
i, j
by computing the culling for a set of p ×q
squares
k,l
i, j
= {B
i−p+k, j−q+l
, B
i−p+k+1, j−q+l
,
B
i−p+k, j−q+l+1
, B
i−p+k+1, j−q+l+1
}
(4)
with 0 ≤ k ≤ p −1 and 0 ≤ l ≤ q −1. Each square
is the convex hull polygon corresponding to the ad-
jacent control points. If any of these squares is not
culled, then the KSQuad is not culled. A KSQuad
i, j
is contained in the convex hull defined by the con-
trol points {B
i−p, j−q
,··· , B
i, j
}. That is, the NURBS
surface fragment that defines the parametric subset
KSQuad
i, j
is contained by the control net fragment,
p ×q squares. If any square is oriented to the view-
point, then it is possible that any point in the surface
is frontfaced. The control polygon represents a piece-
wise bilinear approximation to the surface. This ap-
proximation is improved by applying either knot in-
sertion or degree elevation. As a general rule, the
lower the degree, the closer the surface follows its
control polygon, reaching the extreme case with p =
1, when the surface is the control polygon. SQC is
a conservative PVS technique where the EVS is fully
included, as only invisible geometries are discarded,
and a high quality images are rendered.
Figure 5 shows two different scenarios for apply-
ing our culling strategies: for a high-degree surface
(Figure 5a), there are few knots in the NURBS and the
difference between the results obtained by the approx-
imative and the conservative strategies,
i, j
and
k,l
i, j
,
is greater; however, for a low-degree surface (Fig-
ure 5b) the squares
i, j
comes close to the actual sur-
face, so a similar PVS is obtained in both strategies,
although with an marked reduction in performance in
the approximative method (as shown in Section 5).
The introduction of these Quad Culling techniques
in RPNS results in an important reduction in the com-
putational load of the sampler and rasterizer stages,
although this is accompanied by a slight increase in
the computation of the geometry stage.
Efficient Culling Techniques for Interactive Deformable NURBS Surfaces on GPU
21
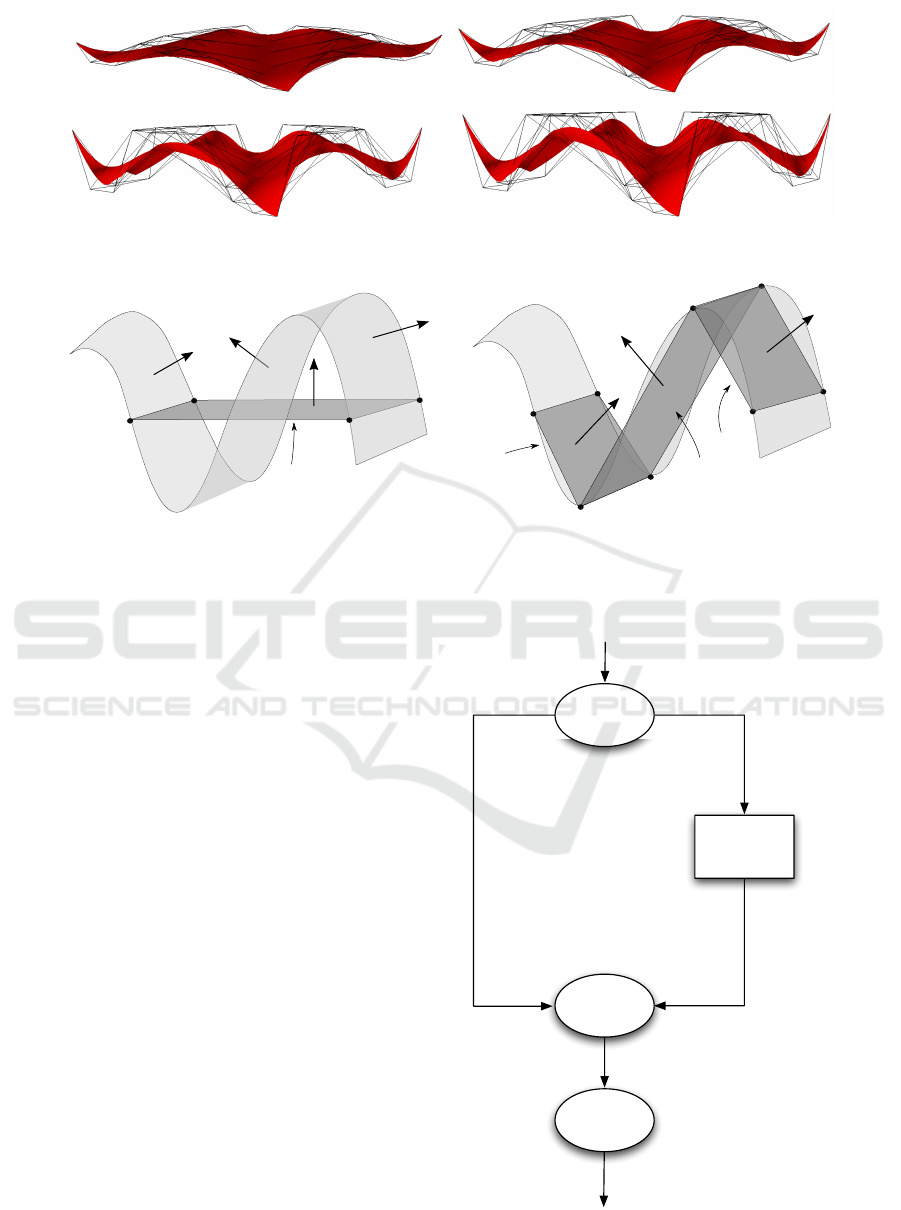
Figure 4: Example of NURBS surface deformation.
KSQuad
S(x
i
, y
j+1
)
S(x
i
, y
j
)
S(x
i+1
, y
j+1
)
S(x
i+1
, y
j
)
(a)
KSQuad
k
KSQuad
k+1
S(x
i
,y
j+1
)
S(x
i
,y
j
)
S(x
i+1
,y
j
)
S(x
i+1
,y
j+1
)
S(x
i+2
,y
j+1
)
KSQuad
k+2
S(x
i+3
,y
j
)
S(x
i+2
,y
j
)
S(x
i+3
,y
j+1
)
(b)
Figure 5: KSQuad-based culling (a) high degree NURBS (b) low degree NURBS.
4 TECHNIQUES OF CULLING
ON CURRENT GPUS USING
DIRECTX11
With DirectX11 three new stages (hull shader, tessel-
lator unit and domain shader) were introduced to sup-
port programmable tessellation (Sch
¨
afer et al., 2014).
These stages are inserted between the vertex and the
geometry shader. The hull shader and the domain
shader are programmable stages, whereas the unit
where the real data expansion happens, the tessella-
tor, is a configurable stage. Figure 6 depicts how
a KSQuad is processed in DirectX11 according to
RPNS proposal.
Hull shader is invocated once for each input primi-
tive, KSQuad in our proposal. It is the first stage of the
tessellation procedure and it configures tessellator and
domain shader execution. Hence, hull shader gener-
ates two different outputs to guide the tessellation pro-
cedure, one output is sent to the domain shader while
the other one is sent to the tessellator. Both outputs in-
clude the tessellation factors which are generated on-
the-fly in the hull shader. In this shader a view frus-
tum culling is applied for each KSQuad. Furthermore,
LQC or SQC could be chosen to cull out KSQuad ear-
lier in the pipeline.
Domain shader receives the parametric coordi-
Hull
Shader
HS input: KSQuad
Domain
Shader
Tessellator
HS output:
if No culling
- KSQuad control points
- Tessellation factors
HS output:
- Tessellation factors
Tessellation output:
- Samples KSDice
(parametric coordinates)
Geometry
Shader
Domain output:
- KSDice
Geometry output:
if no culling
- KSDice Triangles
Figure 6: KSQuad processing in RPNS on DirectX11.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
22

nates from the tessellator as well as the input prim-
itive and the tessellator factors from the hull shader.
According to the received data, these parametric co-
ordinates are evaluated in the domain shader, that is
invocated once for each parametric coordinate gen-
erated in the tessellator. The four corners of each
KSDie, S(x
k
,y
l
), S(x
k
+ δ
x
,y
l
), S(x
k
,y
l
+ δ
y
), and
S(x
k
+ δ
x
,y
l
+ δ
y
), are efficiently evaluated in the DS
by taking advantage of access locality and avoiding
redundant computations. Let us emphasize that like
Reyes vertex shading, RPNS also allows the user to
specify an arbitrary shading rate. In Reyes, shading
rate is expressed in samples per pixel meanwhile we
specify samples per KSDie in RPNS, with a value of
4.0 in our implementation. A more efficient RPNS
implementation would adaptively choose the shading
rate per KSDie, but that objective is beyond the scope
of this paper.
The output from the DS is sent to the Geometry
Shader, where two triangles are generated for each
KSDie due to the triangle-oriented graphics pipeline
of current GPUs. Furthermore, to optimize the ren-
dering of NURBS surfaces we include the evaluation
of EVS in the Geometry shader. This culling stage
has a high impact on the overall performance, since
it achieves an important reduction in the number of
KSDice to get rasterized. On the other hand, in the
Geometry Shader, the KSDie could be sampled again
in order to assure that a higher subdivision level is
applied to non-flat regions. Furthermore, a bound-
ary region test detects the regions of KSDice that are
boundaries to other surfaces and applies the highest
subdivision factor to prevent cracks between adjacent
surfaces.
5 EXPERIMENTAL RESULTS
In this section we present the results obtained with
our culling methods implemented in RPNS. Our test
platform is an Intel Core 2 Duo 2.4GHz with 2GB
of RAM and a NVidia Geforce 580 GTX with Di-
rectX11, Microsoft’s HLSL. The models used in our
tests are shown in Figure 7 and Table 1 depicts the
number of NURBS surfaces and KSQuads, #NS and
#KS, respectively, in the models. As shown in Ta-
ble 1 a high #KS and a low #NS are desirable due to
the fact that a high amount of #KS provides a high
flexibility and adaptivity inside the NURBS surface
meanwhile a low #NS decreases the continuity gaps,
because they can only be introduced on surface edges.
The final images were rendered with a screen resolu-
tion of 2048 ×1152 pixels.
This analysis focuses on the number of primitives
Table 1: Number of surfaces and KSQuad for each test
model.
Test model #NS #KS
Killeroo 89 11532
Head 601 15025
Hinge 427 34891
Car 1364 63000
generated, the quality of the rendered images, as well
as the frame rate achieved. The results obtained from
the tests are shown in detail in Table 2, Table 3, Ta-
ble 4. The experiments were carried out for the four
test models for different culling strategies and with
different values of the threshold µ (maximum pixel-
size for each KSDice, see Equation 2).
Table 2 depicts the thousands of KSDice that are
rendered, #KS, and Table 3 shows the PSNR value
(Peak Signal-to-Noise Ratio in dB) for each config-
uration to provide performance in terms of quality.
Peak Signal-to-Noise Ratio is the distortion between
the maximum possible power of a signal and the
power of corrupting noise that affects the fidelity of its
representation. In this case, the distortion is measured
with respect to the model rendered with the maximum
tessellation factor PSNR = 20 ·log
10
(MAX/
√
MSE).
As can be observed, similar results have being ob-
tained in all cases. Finally, the frame rate achieved,
FPS, is shown in Table 4 to provide performance in
terms of rendering time.
For each culling technique implemented, Table 2
shows the percentage of KSDice eliminated. The
Strong Quad Culling approach culls up to 44.45%
of primitives, but there are still 1.4 times more KS-
Dice than the strictly necessary for the rendering. The
Lightweight approach culls some KSDice that should
be in the rendering, so the quality of the render (PSNR
value) decreases slightly. Anyhow, as PSNR tables
depicts, good quality results are obtained with the
three culling solutions, always over 30dB and close to
40dB for all µ values, with no significant loss of qual-
ity even with the non conservative approach (LQC).
Commonly accepted reference values for PSNR are
between 20 and 40dB (the bigger, the better). A value
higher than 30 dB usually means that a good quality
result has been achieved.
Regarding the frame rate obtained by the differ-
ent culling approaches for the four test models, Ta-
ble 4 shows how SQC achieves the best results. Thus,
for example, speedups of 2.86 and 2.37 are obtained
for µ = 4 by the LQC and SQC, respectively. How-
ever, as the value of µ rises, the number of KSDice
generated for each KSQuad decreases (see Table 2);
this means that for values lower than 300 K KSDice
the high computational cost of the HS software imple-
Efficient Culling Techniques for Interactive Deformable NURBS Surfaces on GPU
23

(a) Killeroo
(b) Head
(c) Hinge
(d) Car
Figure 7: Test models.
Table 2: Thousands of #KS obtained with the different culling techniques for the four test models.
(a) Killeroo
µ = 1 µ = 2 µ = 4
No Culling 1564.79 485.76 178.47
DC
847.16 261.89 95.72
54.14% 53.91% 53.63%
SQC
1564.79 378.63 139.71
100% 77.95% 78.29%
LQC
841.98 259.90 94.82
53.81% 53.5% 53.13%
(b) Head
µ = 1 µ = 2 µ = 4
No Culling 2309.04 742.09 225
DC
1223.83 368.87 131.85
53% 49.71% 58.6%
SQC
1829.71 554.62 199.82
79.24% 47.74% 88.81%
LQC
1211.38 368.28 131.23
52.45% 49.63% 58.33%
(c) Hinge
µ = 1 µ = 2 µ = 4
No Culling 4245.46 1593.56 576.54
DC
1578.48 716.35 252.02
62.81 % 55.04 % 56.28%
SQC
2977.54 907.97 325.36
29.86% 43.02% 43.56%
LQC
2373.27 716.07 251.76
44.09 % 55.06% 56.33%
(d) Car
µ = 1 µ = 2 µ = 4
No Culling 4448.50 1493.51 607.11
DC
2520.33 839.08 311.96
56.66% 56.18% 51.38%
SQC
3444.57 1149.10 459.18
56.81% 56.22% 55.25%
LQC
2527.32 839.68 335.44
77.43% 76.94% 75.63%
mentation, that has a significant degree of divergence,
spoils the advantage achieved by reducing the number
of KSDice to be rendered in cases with similar tessel-
lation factors for all the surfaces, so the frame rate
drops. In this case, the best results are obtained by the
Dice Culling implementation, since the backface KS-
Dice are removed with very simple computations with
no divergence on the GS. Otherwise, the BackPatch
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
24

Table 3: PSNR obtained with the different culling techniques for the four test models.
(a) Killeroo
µ = 1 µ = 2 µ = 4
No Culling 44.51 42.95 40.75
DC 44.50 42.95 40.75
SQC 44.53 42.95 40.75
LQC 39.16 38.64 38.22
(b) Head
µ = 1 µ = 2 µ = 4
No Culling 42.37 43.93 42.97
DC 42.36 43.86 42.57
SQC 42.36 43.95 42.57
LQC 38.88 38.41 38.21
(c) Hinge
µ = 1 µ = 2 µ = 4
No Culling 41.89 41.39 39.77
DC 41.02 41.65 39.94
SQC 41.11 41.42 39.78
LQC 40.60 41.29 39.70
(d) Car
µ = 1 µ = 2 µ = 4
No Culling 38.64 38.35 40.47
DC 38.53 38.34 40.45
SQC 38.54 38.34 40.48
LQC 34.87 34.47 35.25
Table 4: FPS obtained with the different culling techniques for the four test models (speedup against no culling is also shown).
(a) Killeroo
µ = 1 µ = 2 µ = 4
No Culling 27.91 76.14 152.7
DC 26.43 73.1 165.21
0.95x 0.96x 1.08x
SQC 34.46 87.51 162.78
1.23x 1.15x 1.06x
LQC 47.44 107.12 179.9
1.70x 1.41x 1.18x
(b) Head
µ = 1 µ = 2 µ = 4
No Culling 17.90 41.84 113.03
DC 20.66 54.6 158.48
1.15x 1.30x 1.40x
SQC 21.44 49.83 54.56
1.20x 1.19x 0.48x
LQC 33.67 90.24 122.52
1.88x 2.16x 1.08x
(c) Hinge
µ = 1 µ = 2 µ = 4
No Culling 9.27 27.57 35.22
DC 8.55 26.21 64.94
0.92x 0.95x 1.84x
SQC 15.35 44.49 83.42
1.66x 1.61x 2.37x
LQC 19.01 53.73 100.65
2.05 1.95 2.86
(d) Car
µ = 1 µ = 2 µ = 4
No Culling 10.23 20.31 33.3
DC 9.59 29.91 59.18
0.94x 1.47x 1.77x
SQC 12.85 34.9 58.9
1.26x 1.72x 1.77x
LQC 17.06 44.37 70.56
1.67x 2.18x 2.12x
Culling implementations may still be worthwhile for
values between 300 K and 200 K KSDice in mod-
els such as Killeroo. In this model, there are KSDice
with much higher tessellation factors than others as
they have a greater area in the projected image. These
large KSQuads are an important bottleneck, so perfor-
mance dramatically improves when they are culled.
Thus, 182.7 K KSDice are generated without culling
with µ = 4 for the Killeroo model, achieving 179.9
and 165.21 f ps with the LQC and the DC solutions,
respectively. Therefore, BackPatch Culling attains the
best performance results for the more complex mod-
els, those for which the profit of culling is more no-
ticeable.
Regarding the performance attained with our im-
plementations in the pipeline of current GPUs, Ta-
Efficient Culling Techniques for Interactive Deformable NURBS Surfaces on GPU
25
0
100
200
300
400
1 2 4
0
100
200
300
400
Noculling
LQC
SQC
DC
F P S
µ
(a) Killeroo
0
100
200
300
400
1 2 4
0
100
200
300
400
Noculling
LQC
SQC
DC
F P S
µ
(b) Head
0
50
100
150
1 2 4
0
50
100
150
F P S
Noculling
LQC
SQC
DC
µ
(c) Hinge
0
20
40
60
80
100
1 2 4
0
20
40
60
80
100
F P S
Noculling
LQC
SQC
DC
µ
(d) Car
Figure 8: Frame rate with the different culling approaches for the four test models.
(a)
(b)
Figure 9: Model Head rendered (a) without any culling (b) with culling.
ble 4 shows the good results in terms of frame rate
obtained with µ ≥ 1 for the four test models. These
results are also depicted in the graphs of Figure 8.
The tables and the graphs show that the introduc-
tion of BackPatch culling dramatically improves the
performance of the pipeline, with speed-ups of more
than 2x in the frame rate in some cases, and with-
out decreasing the quality in the rendering, since the
PSNR values are mostly identical. In these cases,
the number of primitives culled in an early stage of
the pipeline is not worth the additional computation
introduced with these backpatch strategies such as
LQC and SQC. Backpatch culling strategies are ap-
plied to KSQuad primitives in an early pipeline stage,
while KSDice primitives are culled out in a latter GPU
pipeline stages in a more classical backface culling
approach. Consequently, backpatch culling strategies
evaluate considerable fewer primitives than the back-
face culling strategy. In any case, the final render-
ing obtained by RPNS is a high quality image, as
proved by the PSNR results. Two different renders of
the model Head are shown in Figure 9, without any
culling on the left and with it on the right.
To sum up, the culling techniques proposed in this
work remove an average of around a 20% of the KS-
Dice generated in the case of the SQC method and
over a 41% when the LQC is applied. Both strategies
achieve good results in terms of quality, always over
30 dB, as has previously been mentioned.
6 CONCLUSIONS
In this paper, we provide culling techniques to
NURBS surfaces which cull earlier stage of the
pipeline to reduce as soon as possible the num-
ber of primitives to be processed. Specifically, we
have developed two new efficient culling techniques,
Lightweight BackPatch Culling (LQC) andStrong
BackPatch Culling (SQC), based on the strong convex
hull property of NURBS surfaces that allows a small
culling overhead compared to the computational sav-
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
26

ings, Our proposals have been implemented in Di-
rectX11 to achieve interactive handling of NURBS
surfaces. SQC achieves up to 2.37x speedup over
non-culling proposal whereas LQC up to 2.86x.
As future work, our primary focus is to apply our
culling proposal to handle motion blur rasterization
(Gribel et al., 2013). We also plan to extend our pro-
posal to consider self-collision detection (Wong et al.,
2014).
ACKNOWLEDGEMENTS
This research has been supported by the Gali-
cian Government (Xunta de Galicia) under the
Consolidation Program of Competitive Reference
Groups, cofunded by FEDER funds of the EU (Ref.
GRC2013/055); and by the Ministry of Economy and
Competitiveness of Spain and FEDER funds of the
EU (Project TIN2013-42148-P).
REFERENCES
Akenine-M
¨
oller, T., Haines, E., and Hoffman, N. (2008).
Real-Time Rendering. A. K. Peters.
Claux, F., Barthe, L., Vanderhaeghe, D., Jessel, J.-P., and
Paulin, M. (2014). Crack-free rendering of dynam-
ically tesselated B-rep models. Computer Graphics
Forum, 33(2):263–272.
Cohen, E., Lyche, T., and Riesenfeld, R. (1980). Discrete B-
splines and subdivision techniques in computer-aided
geometric design and computer graphics. Computer
Graphics and Image Processing, 14(2):87–111.
Concheiro, R., Amor, M., and B
´
oo, M. (2010). Synthe-
sis of B
´
ezier surfaces on the GPU. In Richard, P.,
Braz, J., and Hilton, A., editors, Proceedings of the
GRAPP’10: International Conference on Computer
Graphics Theory and Applications, pages 110–115.
INSTICC Press.
Concheiro, R., Amor, M., Padr
´
on, E. J., and Doggett, M. C.
(2014). Interactive rendering of NURBS surfaces.
Computer-Aided Design, 56:34–44.
Gribel, C. J., Munkberg, J., Hasselgren, J., and Akenine-
M
¨
oller, T. (2013). Theory and analysis of higher-order
motion blur rasterization. In Proceedings of the 5th
High-Performance Graphics Conference, HPG’13,
pages 7–15.
Guthe, M., Bal
´
azs,
´
A., and Klein, R. (2005). GPU-based
trimming and tessellation of NURBS and T-Spline
surfaces. ACM Transactions on Graphics, 24(3).
Hasselgren, J., Munkberg, J., and Akenine-M
¨
oller, T.
(2009). Automatic pre-tessellation culling. ACM
Trans. Graph., 28(2):19:1–19:10.
Krishnamurthy, A., Khardekar, R., and McMains, S. (2007).
Direct evaluation of NURBS curves and surfaces on
the GPU. In Proceedings of SPM’07: The 2007 ACM
Symposium on Solid and Physical Modeling, pages
329–334.
Krishnamurthy, A., Khardekar, R., McMains, S., Haller, K.,
and Elber, G. (2009). Performing efficient NURBS
modeling operation on the GPU. IEEE Transactions
on Visualization and Computer Graphics, 15(4):530–
543.
Kumar, S., Manocha, D., and Lastra, A. (1996). Inter-
active display of large-scale NURBS models. IEEE
Transactions on Visualization and Computer Graph-
ics, 2(4):323–336.
Loop, C. T., Nießner, M., and Eisenacher, C. (2011). Effec-
tive back-patch culling for hardware tessellation. In
Proceeding of the VMV 2011: Vision, Modeling, and
Visualization Workshop, pages 263–268.
Munkberg, J., Hasselgren, J., Toth, R., and Akenine-M
¨
oller,
T. (2010). Efficient bounding of displaced B
´
ezier
patches. In Proceedings of the Conference on High
Performance Graphics, HPG’10, pages 153–162. Eu-
rographics.
Nießner, M. and Loop, C. (2012). Patch-based occlusion
culling for hardware tessellation. In Proceedings of
the Computer Graphics International 2012, CGI’12.
Nießner, M., Loop, C., Meyer, M., and DeRose, T. (2012).
Feature adaptive GPU rendering of Catmull-Clark
subdivision surfaces. ACM Transactions on Graphics,
31(1).
Pfister, H., Zwicker, M., van Baar, J., and Gross, M. (2000).
Surfels: surface elements as rendering primitives. In
Proceedings of the SIGGRAPH’00: 27th annual con-
ference on Computer graphics and interactive tech-
niques, pages 335–342, New York, NY, USA. ACM
Press/Addison-Wesley Publishing Co.
Piegl, L. and Tiller, W. (1997). The NURBS Book. Springer.
Sch
¨
afer, H., Nießner, M., Keinert, B., Stamminger, M., and
Loop, C. (2014). State of the art report on real-time
rendering with hardware tessellation. In Eurograph-
ics, State of the Art Reports.
Sederberg, T. W. and Meyers, R. J. (1988). Loop detection
in surface patch intersections. Computer Aided Geo-
metric Design, 5(2):161–171.
Shen, J., Kosinka, J., Sabin, M. A., and Dodgson, N. A.
(2014). Conversion of trimmed NURBS surfaces to
CatmullClark subdivision surfaces. Computer Aided
Geometric Design, 13(7–8):486–498.
Shirman, L. A. and Abi-Ezzi, S. S. (1993). The cone of nor-
mals technique for fast processing of curved patches.
Computer Graphics Forum, 12(3):261–272.
Smith, J. and Schaefer, S. (2015). Selective degree elevation
for multi-sided B
´
ezier patches. Computer Graphics
Forum, 34(2).
Wong, S.-K., Lin, W.-C., Wang, Y.-S., Hung, C.-H., and
Huang, Y.-J. (2014). Dynamic radial view based
culling for continuous self-collision detection. In Pro-
ceedings of the 18th meeting of the ACM SIGGRAPH
Symposium on Interactive 3D Graphics and Games,
I3D’14, pages 39–46.
Yeo, Y. I., Bin, L., and Peters, J. (2012). Efficient pixel-
accurate rendering of curved surfaces. In Proceedings
of the i3D’12: ACM SIGGRAPH Symposium on Inter-
active 3D Graphics and Games, pages 165–174, New
York, NY, USA. ACM.
Efficient Culling Techniques for Interactive Deformable NURBS Surfaces on GPU
27
