
Content based Computational Chromatic Adaptation
Fatma Kerouh
1,2
, Djemel Ziou
3
and Nabil Lahmar
3
1
Institute of Electrical and Electronic Engineering, M’Hamed BOUGARA University, Boumerdes, Algeria
2
USTHB, Image Processing and Radiation Laboratory, Algiers, Algeria
3
D
´
epartement d’Informatique, Universit
´
e de Sherbrooke, Sherbrooke, Qc., J1K 2R1, Canada
Keywords:
Computational Chromatic Adaptation, von Kries Transform, Bradford Transform, Sharp Transform, Spatial
Content.
Abstract:
Chromatic adaptation is needed to accurately reproduce the color appearance of an image. Imaging systems
have to apply a transform to convert a color of an image captured under an input illuminant to another output
illuminant. This transform is called Chromatic Adaptation Transform (CAT). Different CATs have been pro-
posed in the literature such as von Kries, Bradford and Sharp. Both these transforms consider the adjustment
of all the image spatial contents (edges, texture and homogeneous area) in the same way. Our intuition is that,
CATs behave differently on the image spatial content. To verify that, we prospect to study the well known
CATs effect on the image spatial content, according to some objective criteria. Based on observations we
made, a new CAT is derived considering the image spatial content. To achieve that, suitable requirements for
CAT are revised and re-written in a variational formalism. Encouraging results are obtained while comparing
the proposed CAT to some known ones.
1 INTRODUCTION
The Human Visual System (HVS) has the partic-
ularity of dynamically adapting to the changing
of light conditions. In fact, HVS is able to carry
out automatically a chromatic adaptation in order
to preserve color constancy. However, imaging
systems as scanners and digital camera have not
the ability to adjust their sensors relative response
as the HVS. In this case, a transform is needed. It
is called Chromatic Adaptation Transform (CAT).
Computational color adaptation refers to the use of
algorithms to predict the real color of an object when
it is seen and captured under different light sources.
It is a basic operation in the color appearance model
(Fairchild, 2005) (Madin and Ziou, 2014), where
the goal is to provide complete and faithful color
information that fulfils the requirements of real
world applications including, white balance (Wilkie
and Weidlich, 2009), (Laine and Saarelma, 2000),
(Lee and Goodwin, 1997), (Hirakawa and Parks,
2005), (Spitzer and Semo, 2002), color reproduction
(Fairchild, 2005), and color based skin recognition
(Bourbakis et al., 2007). Assuming the light sources
known, a deterministic prediction is possible if the
image formation model allows to write an output
image as a function of an input image. According
to the von Kries chromatic adaptation theory (Kries,
1970), a color prediction of an object is reached by
independently scaling each sensor output value by
the output to input ratio in the RGB color space. The
implementation is straightforward. The output image
is obtained by multiplying the input image and the
diagonal matrix of ratios
X
0
Y
0
Z
0
= M
−1
α 0 0
0 β 0
0 0 γ
M
X
Y
Z
(1)
A linear CAT can be written as M
−1
DM, (equation
(1)), where M is a matrix related to the used color
space and D stands for the von Kries transform. Any
CAT can be seen as a linear transform of a color space
to another one of the same dimension. Where, the
columns of M are the basis of the color space and D
is a diagonal matrix specifying colors dispersion ac-
cording to each element of the basis. Given the input
color space and the von Kries transform, another is-
sue concerns the choice of the output color space. In
some previous works, the space is obtained experi-
mentally by color matching paradigms where the cri-
teria to choose the color space are implicit. However,
Kerouh, F., Ziou, D. and Lahmar, N.
Content based Computational Chromatic Adaptation.
DOI: 10.5220/0005678100390047
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 2: IVAPP, pages 41-49
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
41

some criteria were established. According to Lam
(Lam, 1985), the CAT should maintain constancy for
all neutrals, work with different adapting illuminant,
and it should be reversible. More theoretical studies
were conducted to identify the requirements to select
the suitable color space for color prediction (Gortler
et al., 2007; West and Brill., 1982). Among these
requirements, narrowing the sensor spectral sensitiv-
ity leads to more accurate color prediction. Based
on these findings, Finlayson et al proposed the Sharp
transform (Finlayson et al., 1994). A quantitative
evaluation and comparison between some existing
transforms can be found in (Luo, 2000; Holm et al.,
2010; Bianco and Schettini, 2010). According to
these evaluations, the Bradford, Bartleson, Sharp, and
CMCCAT2000 transforms perform better than many
others. Note that the experimental data set used to
derive the transform is another issue. The available
data sets are chosen according to some protocols and
viewing conditions to reflect realistic situations (Luo,
2000). However, the image content effect on color
prediction is not understood because in most previ-
ous works the whole data are transformed into XY Z
color space coordinates and used to derive a CAT. To
summarize, four research area can be discussed in the
color adaptation field. The first one concerns the best
color space used to implement a CAT. The second is-
sue is about the used transform to adapt the image
color appearance. The third one refers to the choice
of the best output color space and the last research
area concerns the experimental datasets. The purpose
of this work falls under the second research area. Our
aim is to propose a new color adaptation transform
that fulfils some particular requirements.
The image content refers to spatial information
such as edges and textures at low abstraction level
and to events such as objects, their relationships and
context at high abstraction level. For example, the
color prediction at a pixel is independent from the
color of the other pixels. Ignoring spatial correlation,
the transform accuracy can be high in some areas of
an image and low in others. In this paper, we em-
pirically studied the influence of CATs on the low
level image content (which we call the spatial con-
tent) that are colors, edges, textures and homogeneous
areas. Based on conclusions we made and inspired
by the Sharp transform proposed earlier by Finlayson
et al.(Finlayson et al., 1994), we propose new con-
straints and formulate the derivation of CAT as a vari-
ational problem. The resulting transform is compared
to some existing transforms based on the von Kries
theory. The next section is devoted to studying the
CATs influence on image spatial information. In Sec-
tion 3, we present a new proposed approach to derive
a CAT. Experimental results are addressed in Section
4. The last section concludes this work with some
valuable issues.
2 COMPUTATIONAL
CHROMATIC ADAPTATION
EFFECT ON THE IMAGE
CONTENT
In this section, a series of tests are conducted allowing
to understand the von Kries-based CATs effect on im-
ages spatial content. In our experiments, we pay par-
ticular attention to edges, texture and homogeneous
areas. Texture is characterized by its form, coarse-
ness and complexity while edges are characterized by
their sharpness and orientation.
2.1 Test Data
The reliability of experiments on chromatic adapta-
tion depends on the test data accuracy. In our experi-
ments, the used images are built using the image for-
mation model. For a surface with a reflectance func-
tion R(λ) and an illuminant E(λ), the discrete image
formation model is given by:
X = C
700
∑
λ=400
E(λ)R(λ)VW X(λ) (2)
Y = C
700
∑
λ=400
E(λ)R(λ)VWY(λ) (3)
Z = C
700
∑
λ=400
E(λ)R(λ)VW Z(λ). (4)
Where,
• VW X , VWY and VWZ are considered as the VW
sensor sensitivities (Finlayson et al., 1994).
• Reflectance images R, are taken from the G. Fin-
layson et al. collection (Finlayson et al., 2004).
This collection consists of a set of reflectance im-
ages of everyday objects with high spatial and
spectral resolutions.
• The incandescent illuminant A and daylight D65,
which are experimental illuminant approved by
the CIE (CEI, 1998), are used.
• The constant C = 100
.
∑
700
λ=400
E(λ)VWY (λ) is
used for normalization, yielding a value of Y =
100 for a perfect diffuser, which means that the re-
flectance is equal to one for all wavelengths (Lee
and Goodwin, 1997). The wavelengths are sam-
pled by an increment of 10nm in the visible inter-
val [400,700]nm.
IVAPP 2016 - International Conference on Information Visualization Theory and Applications
42

• Finally, to display the image, the sRGB space is
used. This color space is proposed by Hewlett-
Packard and Microsoft via the International Color
Consortium ICC (Stokes et al., 1996).
Having the reflectance multispectral images R, vari-
ous test images could be constructed, according to the
image formation model, using different light sources
E and VW sensors sensitivity.
2.2 Methodology
The aim now is to study the CATs effect on the image
content (homogeneous area, edges and texture). To
achieve that, the following steps are followed.
• Twenty-three reflectance images of various ob-
jects and two standard illuminant (illuminant
”D65” and illuminant ”A”) are used to construct
test images using the image formation model as
explained before. Altogether, there are 46 test
images categorized in groups, which we will call
groupA and groupD65.
• Consider a pair of images of the same scene
taken under the standard illuminant ”D65” and
”A”. The aim is to transform the test image un-
der ”D65” to the estimated image under ”A” by
using the von Kries based CATs. According to
our experimentation, we found that the Bradford
transform (CAT
B
) provides the smallest distortion
of the estimated images. Consequently, in the
remainder of this section we will present only
the scores of CAT
B
. Hence, a third set of im-
ages, groupD65A, is built from groupD65 by us-
ing CAT
B
.
• To evaluate distortions on step edge pixels, we
consider the edge magnitude and orientation. For
this purpose, we compute the mean ν, the vari-
ance σ
2
and the phase θ of the gradient images as
follows:
ν =
1
N × M
∑
i
∑
j
|||G(i, j)|| − ||G
re f
(i, j)||| (5)
σ
2
=
1
N × M
∑
i
∑
j
(|||G(i, j)||−||G
re f
(i, j)|||−ν)
2
(6)
θ = arccos
G · G
re f
kGkkG
re f
k
(7)
where G and G
re f
are the gradient vectors of the
estimated and reference N × M images, respec-
tively and · is the dot product. Note that, the gra-
dient is estimated by using the first partial deriva-
tives of Gaussian.
• To assess the CAT
B
effect on texture, a quanti-
tative evaluation requires to use texture descrip-
tors that allow measuring deformation. For this
purpose, we use nine descriptors estimated from
four cooccurrence matrices, corresponding to dis-
placements equal to one in directions 0, π/4, π/3,
and 3π/2. The computation rules for these de-
scriptors can be found in (Haralick et al., 1973).
The squared Euclidean distance between the tex-
ture descriptors of the estimated and reference im-
ages is used to measure the CAT
B
effect.
• To quantify the distortion between the adapted
and the reference image, S-CIELAB error pre-
diction metric is considered. However, for com-
plex scenes, it should be noted that the varia-
tion of CIELAB ∆E
94
is greater than the variation
of S-CIELAB ∆E
s
(Aldaba et al., 2006), but the
shape of both variations is similar. Hence, we pro-
pose to use the color difference formula CIELAB
∆E
94
between the adapted and the reference im-
age. The ∆E
94
between two colors (L
1
,a
1
,b
1
)
and (L
2
,a
2
,b
2
) is computed as follows (Green and
MacDonald, 2002):
∆E
94
=
"
∆L
k
L
S
L
2
+
∆C
ab
k
C
S
C
2
+
∆H
ab
k
H
S
H
2
#
1
2
(8)
Where ∆L = L
1
− L
2
stands for the luminosity,
∆C = C
1
− C
2
the chroma and ∆H = {(∆a)
2
+
(∆b)
2
− (∆C)
2
}
1
2
the hue.
C
1
=
q
a
2
1
+ b
2
1
, C
2
=
q
a
2
2
+ b
2
2
, ∆a = a
1
− a
2
,
∆b = b
1
− b
2
, k
H
= 1, S
L
= 1, S
C
= 1 + 0.045C,
S
H
= 1 + 0.015C, k
C
= k
L
= 1.
Note that, a ∆E
94
of 1.0 is the smallest color dif-
ference that the human eye can notice.
2.3 Experimental Results
For the quantitative evaluation of the adapted images,
∆E
94
color difference is computed between original
and adapted images by considering, all pixels, ho-
mogeneous area and edge pixels. Note that, for the
caused distortion to both texture and edge areas, grey
level images have been considered. Table 1 shows
the mean of ∆E
94
according to the image content. We
can notice that, the metric value changes according
to the image content; it is not the same for edge pix-
els, homogeneous areas and overall the image pixels.
In fact, compared to all pixels, the estimated error
from homogeneous area and edges is about 7% and
3% greater, respectively. Thus we conclude that, the
chromatic adaptation influence depends on the image
spatial content.
Content based Computational Chromatic Adaptation
43
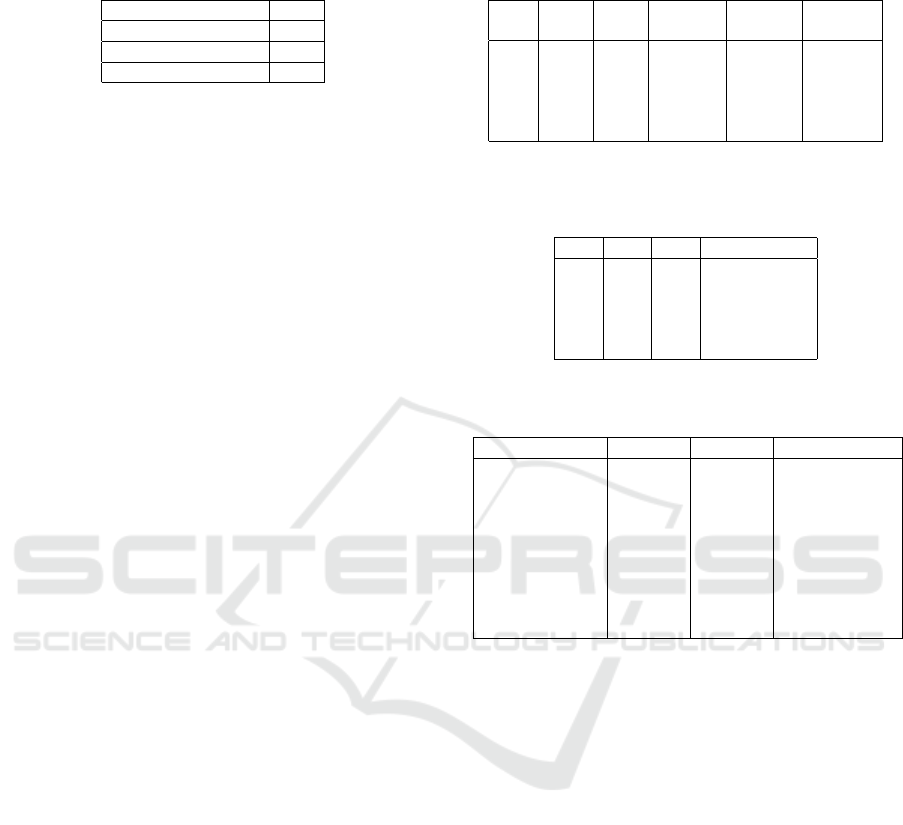
Table 1: Mean of ∆E
94
metric for CAT
Bd f
as a function of
image content.
Image content ∆E
94
All pixels of the image 1.487
Edge pixels 1.535
Homogeneous area pixels 1.589
Our purpose now is to detect which specific char-
acteristics are affected in texture and edges (strength
or orientation or both). For that, as explained in the
methodology sub-section, separate deformation mea-
surement was defined for each image content. Table 2
presents the absolute difference in gradient magnitude
of the two groups of images, groupA and groupD65A,
according to a certain threshold, which is a percent-
age of the maximum value of the gradient magnitude.
Thus a threshold of 5% corresponds to 5% of the max-
imum value of the gradient magnitude in the differ-
ence image. We noticed that, for a threshold (Th)
of 5, 27.473% of all the edge pixels provides a mean
value of 1.183 and a variance value of 0.788; this is
not negligible relatively to the min and the max val-
ues of gradient magnitude, which are 0.454 and 9.078,
respectively. Furthermore, for a threshold of 10, the
percentage of eligible edge pixels is 14.084%, with
a mean value of 1.687 and the associated variance is
1, which is also significant. Based on the obtained
values, we can notice that the mean and the variance
values increase with the threshold, while the percent-
age of eligible edge pixels decreases. Thus, the chro-
matic adaptation transformation produces an image
with less contrast than the reference image, since the
difference in image edges is not negligible. As con-
clusion, edge strength is modified while applying a
CAT.
Table 3 shows the mean and variance of the angle
between the gradient vector of the two groups of im-
ages, according to a certain threshold T h. We notice
a considerable deviation in the gradient. In fact, from
the threshold 5 to 25, the mean of the deviation ranges
from 9.9 to 6.13 degrees. This is significant consider-
ing the percentage of eligible gradient vectors which
are between 36.85% and 6.85%. To summarize:
• While increasing the threshold value, both the
mean and the variance of the absolute difference
in magnitude of gradients increase. However, the
percentage of eligible edge pixels decreases.
• The mean over the smallest and highest gradient
magnitudes ratios show that, the CAT
B
effect is
stronger for details than it is for obvious edges.
• Both the mean error and variance of edge orien-
tation decrease when the smallest gradient magni-
tude increases. Again, details are the most vulner-
able.
Table 2: Mean and variance of in gradient magnitude of the
two image groups, according to empirical threshold.
T h ν σ
2
Max grad Min grad % of edge
pixels
5% 1.183 0.788 9.078 0.454 27.47
10% 1.687 1.000 9.078 0.908 14.08
15% 2.215 1.313 9.078 1.362 7.362
20% 2.875 1.773 9.078 1.816 3.644
25% 3.592 2.084 9.078 2.270 1.998
Table 3: Mean and variance of gradient angle between gra-
dient vectors of the two image groups, according to empiri-
cal threshold.
T h ν σ
2
% of edge pixels
5% 9.90 0.23 36.85
10% 8.62 0.20 22.43
15% 7.54 0.25 14.64
20% 6.63 0.19 10.15
25% 6.13 0.17 6.85
Table 4: Texture characteristics for displacement equal to 1
in the direction 0
◦
.
Features Ref Ad Euclidean distance
Mean 15.248 14.762 0.486
Variance 52.115 50.544 1.571
Energy 0.031 0.030 0.001
Entropy 4.138 4.140 0.001
Contrast 2.086 2.238 0.152
Homogeneity 0.779 0.775 0.004
Correlation 51.073 49.426 1.647
Cluster Shade 1137.740 954.656 183.080
Cluster Prominence 73821.300 66636.700 7184.660
Obtained texture features using groupA and
groupD65A image sets are tabulated on Table 4. The
Euclidean distance is used to perform a one-to-one
comparison of these characteristics computed on a
reference image (Ref) and an adapted one (Ad). No-
tice that, the two features that undergo a significant
change are the shade and the prominence. The vari-
ation in cluster shade implies that the image loses its
symmetry. While change in prominence means that,
the number of pixels having grey levels close to the
mean changes.
To conclude, CAT
B
depends on the image spa-
tial content. Indeed, homogeneous areas colors are
more distorted than edge areas colors. The orienta-
tion and magnitude of weak edges are more distorted
than those of obvious edges. For texture, the shade
and prominence are the most deformed. Hence, our
aim in the next section is to propose a new CAT tak-
ing the image spatial contents into consideration.
IVAPP 2016 - International Conference on Information Visualization Theory and Applications
44

3 SPATIAL COMPUTATIONAL
CHROMATIC ADAPTATION
An image can be seen as the summation of several
cues such as shading, shadow, blur, edges and tex-
tures originating from physical phenomena which are
illumination, reflectance and sensor sensitivity. Based
on observations we made in the previous section, we
can reasonably assume that, the cues behave differ-
ently when a CAT is applied. One can derive a CAT
for each cue. For example, a step edge CAT can be
estimated and used to transform pixels having a high
gradient magnitude. To estimate a CAT, we propose
to revisit the variational formulation of Finlayson et
al. (Finlayson et al., 1994) and include the image data
d(λ) in the new CAT constraints. In addition, the CAT
must fulfil the following requirements:
• Preserving the sensor gamut: This requirement
allows the preservation of the sensed set of col-
ors. Reducing this set, implies a reinforcement of
metamerism. Increasing it may lead to output col-
ors that are not physically realizable on the sensor.
• Reducing the overlap between spectral sensitiv-
ity of colored sensors: As showed in (Finlayson
et al., 1994), this requirement allows a better color
constancy. It can be formalized as a sharpening
problem of sensors spectral sensitivities. Unlike
the formalism of Finlayson et al., the sharpening
of one sensor sensitivity function is related to the
sharpening of the other sensitivity functions of the
same sensor.
• Having a positive sensor response to a given data:
It has been shown that this constraint leads to
more accurate CAT (Drew and Finlayson, 2000).
• Being insensitive to noise: Noise insensitivity is
beneficial, especially, when the CAT is estimated
from real samples that can be noisy. We wish that,
the transform remains unchanged when changing
the variance of a white noise image. However, the
energy of a spectral sensitivity function increases
with the white noise variance because it is equal
to the variance of its response to the centred white
noise. Consequently, the last requirement can be
fulfilled by setting the energy of sensitivity func-
tions to a constant.
More formally, we denote the original sensor sen-
sitivity functions as {b
k
(λ)}
3
k=1
. The sharpening of
this sensor through a linear transform provides new
sensitivity functions noted c
k
(λ) = β
k
B(λ)
t
, where
B(λ) is the original sensor sensitivity functions vec-
tor and β is the linear sharpening transform. In what
follows, we will show how to estimate the sharpening
transform in the case of the k
th
sensitivity function.
The same procedure is applied for the two other sen-
sitivity functions. The response of the k
th
sharpened
sensitivity function to the data d(λ) is given by:
d(λ)c
k
(λ) = d(λ)B(λ)
t
β
k
= D(λ)
t
β
k
.
where β
k
is the vector of sharpening coefficients. Let
Γ be the entire visible interval; Γ = Ω
k
∪Φ
k
, where Φ
k
is the sharpening interval associated with the k
th
sen-
sitivity function. The above mentioned requirements
are translated to:
• Preserving the new sensor Gamut by minimizing
the difference between the responses to the input
data of the original and the new sensitivity func-
tion, that is:
min
β
k
R
Φ
k
(D(λ)
t
β
k
− d(λ)b
k
(λ))
2
dλ
• Reducing the overlap between spectral sensitivi-
ties by minimizing the contribution of the other
spectral sensitivities within the sharpening inter-
val Φ
k
, that is:
min
β
k
R
Φ
k
∑
j6=k
(D
j
(λ)
t
β
j
)
2
dλ and minimizing the
spectral response outside the sharpening interval,
that is:
min
β
k
R
Ω
k
(D(λ)
t
β
k
)
2
dλ
• Reaching a positive solution when
min
β
k
B(λ)
t
β
k
≥ 0, ∀λ ∈ Γ
• Setting the filter energy to one ensuring a robust-
ness of the sharpening transform to the additive
white noise:
R
Ω
k
(B(λ)
t
β
k
)
2
dλ = 1
We will write the discrete version of the variational
problem used to find the optimal β
k
. The combination
of the first, the second and the fourth requirement into
a variational formulation by additive rule is straight-
forward. However, the positivity constraint is not in
an integral form. We propose to use an interior point
formulation, where a logarithm slack function ensur-
ing positivity is used, (Forsgren et al., 2002). Let
us assume that we have N images (or image areas)
taken under different illuminant. We consider ρ and
µ Lagrange multipliers and ε > 0 a barrier parameter
of the slack variables r
k
(λ), assumed positive. More-
over, the importance of each of the above measures is
not defined. One can use a weighted combination of
these measures and estimate the weights. However,
the number of unknowns increases and the estimation
may be under conditioned. We then propose to use
binary weights allowing to identify the relevance of
each measure. Given the color triplets {d
n
}
N
n=1
and
B(λ), the sharpening transform is estimated by mini-
mizing the following objective function:
Content based Computational Chromatic Adaptation
45

Table 5: The four transfer matrices obtained with the image
content-based method.
a
1
a
2
Matrix CAT
1 1 1.1160 −0.045 −0.071 CAT
d11
−0.568 1.3970 0.1710
0.0290 0.0800 0.8910
0 1 1.1260 −0.060 −0.066 CAT
d01
−1.074 1.8470 0.2270
0.0180 0.0820 0.9000
1 0 2.0250 −1.092 0.0670 CAT
d10
−1.716 2.8450 −0.128
0.0440 −0.189 1.1450
0 0 2.1590 −1.206 0.0470 CAT
d00
−1.094 2.1610 0.0670
0.0270 −0.201 1.1740
Ψ
k
(β,µ) = a
1
N
∑
n=1
∑
i∈Φ
k
(D
n
(λ
i
)
t
β
k
−
d
n
(λ
i
)b
k
(λ
i
))
2
δλ +
a
2
N
∑
n=1
∑
i∈Φ
k
∑
j6=k
(D
n
j
(λ
i
)
t
β
j
)
2
δλ +
N
∑
n=1
∑
i∈Ω
k
(D
n
(λ
i
)
t
β
k
)
2
δλ +
ρ(
∑
i∈Γ
(B(λ
i
)
t
β
k
)
2
δλ − 1) +
∑
i∈Γ
µ
i
(B(λ
i
)
t
β
k
− r
k
(λ
i
))δλ − (9)
ε
∑
i∈Γ
log(r
k
(λ
i
))δλ
where D
n
(λ) = d
n
(λ)B(λ) and a
1
anda
2
are the
weighting parameters that have been added to select
the best requirements. The above equations are solved
by using the Newton method to determine β
k
, the La-
grange multipliers µ, ρ, and ε as well as the slack
function r
k
(λ). Note that, the earlier formulation pro-
vided by Finlayson et al. can be obtained by setting
a
1
= a
2
= 0, ρ = 1, ε = 0, µ = 0, and d
n
(λ) = 1. The
formulation with the positivity constraint described
in (Drew and Finlayson, 2000) can be obtained by set-
ting a
1
= a
2
= 0, ρ = 1 and d
n
(λ) = 1. In addition, the
transformation of an image under illuminant a to an
other illuminant b is given by β
−1
D
a,b
β, where D
a,b
is
the von Kries diagonal matrix, and β is the sharpening
matrix where the columns are {β
k
}
3
k=1
. By resolving
the above equation, four transformation matrices are
obtained by combining coefficients a
1
and a
2
which
may be 0 or 1 (Table 5).
Figure 1A depicts the VW sensors and the four
new sensors, obtained by combining both coefficients
a
1
and a
2
. Note that, the combination a
1
= a
2
= 0
corresponds to the sharp transform of Finlayson et al.
According to this figure, two cases are distinguish-
Figure 1: The new sensors in dotted lines compared to the
VW sensor in solid line for each transfer matrix obtained by
the proposed approach.
able, depending on whether coefficient a
1
is 0 or 1.
In the first case (i.e., a
1
= 0), the resulting sensors are
narrower and have greater amplitudes compared to the
VW sensor. In the second case, in contrast, the sen-
sors are larger and their amplitude is smaller than that
of the VW sensor. Another significant remark relates
to the negative values of the spectral distributions of
the sharpened sensors, which are due to negative val-
ues of the calculated transfer matrices. This can cause
color saturation problems during the imaging process.
4 EXPERIMENTAL RESULTS
In this section, we aim to evaluate the four proposed
chromatic adaptation transforms performance. First,
we start by producing test images under illuminants
A and D65. Example of test images are depicted
in figures 2 and 3. Then, we change the illumi-
nant of images under D65 toward illuminant A us-
ing various CAT s (proposed and existing). The com-
parison is carried out between test images generated
using the image formation model under illuminant A
(ground truth) and the adapted ones using different
CAT s. This comparison is achieved following two
evaluation criteria. The first one is related to the per-
ceptual degradation assessment using the color differ-
ence metric presented earlier called ∆E
94
. The second
one is intended to measure the CAT
0
s effect on the im-
age contents defined by edges and texture properties.
IVAPP 2016 - International Conference on Information Visualization Theory and Applications
46

Figure 2: Examples of test images under illuminant D65.
Figure 3: Examples of test images under illuminant A.
Figure 4: ”Freeform” images obtained with the different
CAT transforms, under illuminant A.
Figure 4, illustrates one example of corresponding
images obtained by various CAT s on Freeform image.
4.1 Colorimetric Evaluation
CIE∆E
94
color difference is used, in Lab space, to
estimate the perceptual color difference between the
ground truth and the adapted image. It calculates an
ellipsoid tolerance around the target color, such that
the color belonging to this ellipsoid will be considered
identical. This metric is recommended by CIE for the
color difference quantification. Computed ∆E
94
on
obtained images illustrated in Figure 4 are tabulated
on Table 6. We can notice that, the transformations
CAT Brad f ord( CAT
B
), CAT
d11
, CAT
d10
in that order
provide the best results in terms of perception. How-
ever, the CAT Sharp(CAT
S
) quantitative evaluation is
less acceptable. From ∆E
94
metric stand of point, a
∆E
94
value less than or equal to four is considered to
be satisfactory (CEI, 2004).
Thus we conclude that, the proposed image content
based transform CAT
C11
provides more accurate per-
formance compared to both CATVonKries(C AT
V
) and
CAT
S
. Furthermore, a competitive performance are
noticed against CAT
B
.
4.2 Content-based Evaluation
This evaluation involves calculating some charac-
teristics related to the image content (edges and
texture area) as explained previously. The considered
characteristics are computed on the adapted images
using the proposed CATs and the considered existing
ones (Sharp, Von Kries and Bradford transforms).
Then, the error is quantified using some specific
criteria.
Edge Evaluation
We compute the edge map of the adapted and the
ground truth images. The comparison concerns edges
strength and orientation, as explained previously. Ta-
bles 7, 8 and 9 present the mean and the variance
of the absolute difference between the gradient mag-
nitude of the adapted and the reference images, for
each transformation. Each table is related to a given
threshold. This threshold stands for the percentage of
a gradient magnitudes maximum. It is especially used
to assess the significance of the gradient magnitude
difference, which can be manifested as a difference in
contrast between two image groups. Table 7 presents
the obtained results for a threshold of 5% of the max-
imum value of the gradient magnitude difference in
images. It can be seen that, the CAT
B
transform per-
forms better than the other transformations in terms
of mean values. We note that, Compared to CAT
B
, the
CAT
d11
transform obtains very close results in terms
of mean value and performs better in terms of vari-
ance value and maximum magnitude value. Concern-
ing Tables 8 and 9 which list the results for larger
thresholds, namely 15% and 25%, the CAT
d11
trans-
form obtains the best results in term of mean, variance
and maximum value. All in all, the proposed content-
based transform performs slightly better than the oth-
ers in preserving image edges.
Table 10 shows the mean and the variance values
of the angle between the gradient vectors of the two
image groups for each transformation. The CAT
d11
gradient vector deviation is about 3.431 degrees com-
pared to 6.551 and 8.68 degrees for CAT
B
and CAT
S
,
respectively. According to these results we can argue
that, the proposed CAT
d11
provides the best perfor-
mance in terms of edge pixels orientation preserva-
tion.
Texture Evaluation
We compare the texture descriptors of the reference
and the adapted images as explained in the previous
section. Table 11, shows the Euclidean distance of
Content based Computational Chromatic Adaptation
47
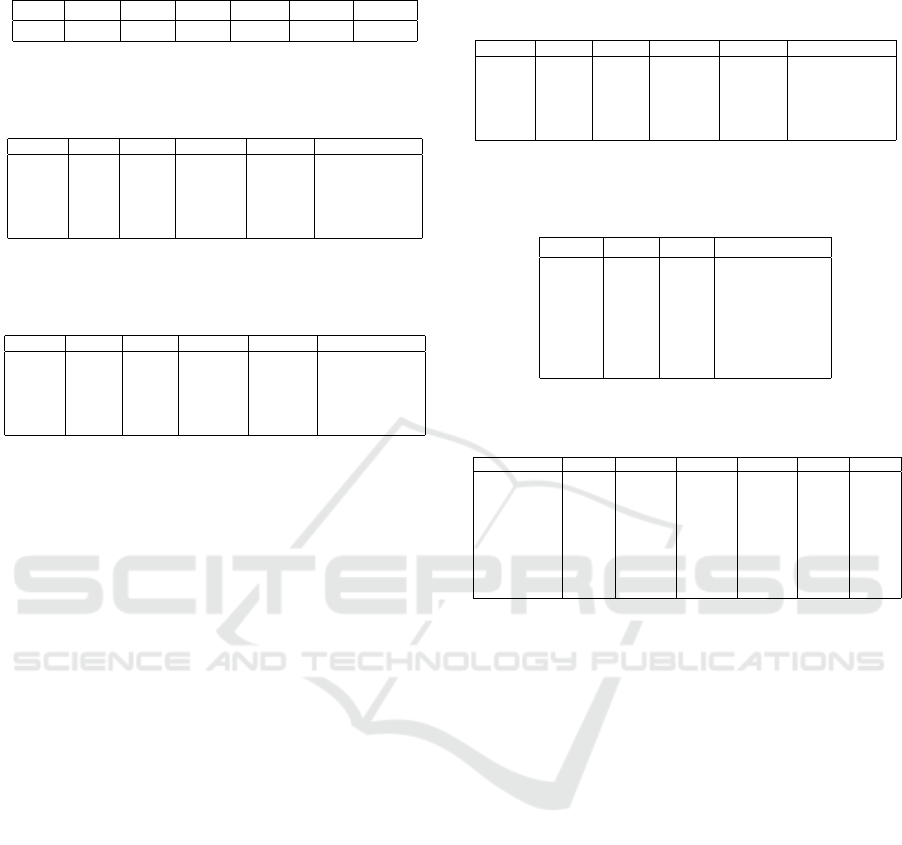
Table 6: Computed color error on images of Figure 4.
CAT
B
CAT
V
CAT
S
CAT
10
CAT
d10
CAT
d11
∆E
94
1.487 2.285 6.377 2.438 2.080 1.92
Table 7: Mean and variance of the absolute difference
in gradient magnitude between the ground truth and the
adapted images for threshold equal to 5%.
ν σ
2
Max grad Min grad % of edges pixels
CAT
S
6.160 21.427 40.083 2.004 23.52
CAT
d01
1.978 2.242 12.347 0.617 35.28
CAT
d10
1.449 1.585 10.085 0.504 23.99
CAT
d11
1.148 0.673 8.989 0.449 29.77
CAT
V
1.804 1.590 11.583 0.579 28.76
CAT
B
1.183 0.788 9.078 0.454 27.47
Table 8: Mean and variance of the absolute difference
in gradient magnitude between the ground truth and the
adapted images for a threshold of 15%.
ν σ
2
Max grad Min grad % of edges pixels
CAT
S
11.222 21.152 40.083 6.013 8.07
CAT
d01
3.362 2.500 12.644 1.897 14.52
CAT
d10
3.940 3.3860 13.254 1.988 15.26
CAT
d11
2.072 1.054 8.988 1.349 9.53
CAT
V
3.070 1.483 11.583 0.738 10.82
CAT
B
2.215 1.313 9.078 0.362 7.362
the texture features, for each transformation matrix.
An ordered ranking of the transformations accord-
ing to the number of texture features where they per-
form, provides (in descending order): CAT
d11
, CAT
B
,
CAT
d10
, CAT
d01
, CAT
V
and CAT
S
. Thus, CAT
d11
is
more accurate in terms of texture mean, contrast,
homogeneity. Especially, cluster shade and cluster
prominence which are the most affected texture prop-
erties according to the previous section. That means
that, these properties are better preserved by the pro-
posed CAT
d11
.
5 CONCLUSION
This paper presents a new chromatic adaptation trans-
forms transform (CAT ) by considering the content in-
formation of a given image. Two main contributions
are proposed. First, the authors prove that the chro-
matic adaptation transform affects differently the im-
age contents, especially edges and texture area which
are two essential elements in the human visual sys-
tem. Second, the authors propose a new reformu-
lation of chromatic adaptation transform (CAT) that
considers the image content information. To achieve
the first purpose, some well knowns CAT s are con-
sidered. According to a perceptual color difference
metric, results prove that these transforms depend
on the image spatial content. Indeed, the homoge-
neous area colors are more distorted than those of
edge areas. Furthermore, edge orientation and mag-
nitude of weak edges are more distorted than those
of obvious edges. For texture, the shade and promi-
Table 9: Mean and variance of the absolute difference
in gradient magnitude between the ground truth and the
adapted images for a threshold of 25%.
ν σ
2
Max grad Min grad % of edges pixels
CAT
S
13.249 18.226 40.083 8.017 5.47
CAT
d01
3.982 2.690 12.644 2.529 9.5
CAT
d10
4.665 3.839 13.254 2.651 10.58
CAT
d11
2.689 1.618 8.988 2.247 4.31
CAT
V
3.658 1.320 11.583 2.317 6.96
CAT
B
2.875 1.773 9.078 2.27 3.64
Table 10: Mean and variance of absolute difference in gra-
dient angle between the the ground truth and the adapted
images for a threshold of 5%.
ν σ
2
% of edge pixels
CAT
S
8.680 0.685 23.52
CAT
d01
5.574 0.197 35.28
CAT
d10
5.913 0.268 23.99
CAT
d11
3.431 0.160 29.77
CAT
V
7.249 0.365 28.76
CAT
B
6.551 0.384 27.47
Table 11: The Euclidean distance of texture features for
each CAT .
Features CAT
S
CAT
d01
CAT
d10
CAT
d11
CAT
B
CAT
V
Mean 0.336 0.283 0.152 0.070 0.174 0.486
Variance 5.993 0.687 0.592 0.462 0.308 1.571
Energy 0.002 0.001 0.001 0.001 0.001 0.001
Entropy 0.107 0.011 0.042 0.006 0.011 0.001
Contrast 0.213 0.106 0.027 0.071 0.072 0.152
Homogeneity 0.022 0.004 0.006 0.000 0.002 0.004
Correlation 5.384 0.740 0.605 0.426 0.343 1.647
Shade 279.2 112.6 77.8 59.61 68.35 183.0
Prominence 10330 4044 2825 900.5 2526 7184
nence features are the most deformed features. Based
on these conclusions, the authors reformulate the
sharp transform considering new CAT
0
s requirements.
From the variational formulation, four transforms
have been proposed. Their performances are quan-
titatively evaluated against some well known trans-
forms (Sharp, Bradford and von Kries). Experimental
results showed that one of these transforms, namely
CAT
d11
, preserves better edges and texture features
than the considered existing CAT s. Thus, taking the
image content into account, to derive CAT s, can im-
prove the preservation of both the color and the spa-
tial content of the adapted images. Future works will
involve the consideration of a large database and es-
pecially noisy data. In addition, the authors prospect
to use other evaluation criteria.
REFERENCES
Aldaba, M. A., Linhares, J. M., Pinto, P. D., Nascimento,
S. M., and K. Amano, D. H. F. (2006). Visual sensi-
tivity to color errors in images of natural scenes. In
Visual Neuroscience, 23:555-559.
Bianco, S. and Schettini, R. (2010). Two new von kries
based chromatic adaptation transforms found by nu-
IVAPP 2016 - International Conference on Information Visualization Theory and Applications
48

merical optimization. In Color Research and Applica-
tion, 35(3):184-192,.
Bourbakis, N., Kakumanu, P., Makrogiannis, S., Bryll, R.,
and Panchanathan, S. (2007). Neural network ap-
proach for image chromatic adaptation for skin color
detection. In Int. Journal of Neural Systems, 17(1):1-
12.
CEI (1998). Commission internationale de l’eclairage.
interim colour appearance model (simple version,
ciecam97s). In Technical Report, 131.
CEI (2004). Commission internationale de l’eclairage. a
review of chromatic adaptation transforms. technical
report, 160. In Visual Neuroscience.
Drew, M. S. and Finlayson, G. (2000). Spectral sharpening
with positivity. In J. Opt. Soc. Am. A, 17:1361-1370,.
Fairchild, M. D. (2005). Color appearance models. In Sec-
ond Edition, Wiley.
Finlayson, G., Drew, M., and Funt, B. (1994). Spec-
tral sharpening: Sensor transformations for improved
color constancy. In J. Opt. Soc. Am. A, 11(5):1553-
1563.
Finlayson, G., Hordley, S., and Morovic, P. (2004). A multi-
spectral image database and an application to image
rendering across illumination. In Int. Conf. on Image
and Graphics, 8-20, Hong Kong.
Forsgren, A., Gill, P., and Wright, M. (2002). Interior meth-
ods for nonlinear optimization. In SIAM Rev, 44:525-
597.
Gortler, S. J., Chong, H. Y., and Zickler, T. (2007). The von
kries hypothesis and a basis for color constancy. In
ICCV, 1-8.
Green, P. and MacDonald, L. (2002). Colour engineering:
Achieving device independent colour. In Wiley.
Haralick, R., Shanmugan, K., and Dinstein, I. (1973). Tex-
tural features for image classification. In IEEE Trans-
actions on Systems, Man, and Cybernetics, 6(3):610-
621,.
Hirakawa, K. and Parks, T. W. (2005). Chromatic adapta-
tion and white-balance problem. In IEEE ICIP, 984-
987.
Holm, J., Susstrunk, S., and Finlayson, G. (2010). Chro-
matic adaptation performance of different rgb sensors.
In SPIE, 172-183.
Kries, J. V. (1970). Chromatic adaptation. In In D.L.
MacAdam, (ed.) Sources of Color Science, The MIT
Press, Cambridge MA, 120-127.
Laine, J. and Saarelma, H. (2000). Illumination-based
color balance adjustments. In Color Imaging Confer-
ence: Color Science, Engineering Systems, Technolo-
gies and Applications, 202-206.
Lam, K. M. (1985). Metamerism and colour constancy. In
Ph.D. Thesis, University of Bradford.
Lee, H. C. and Goodwin, R. M. (1997). Colors as seen by
humans and machinesy. In Recent Progress in Color
Science, 18-22.
Luo, R. (2000). Color constancy: a biological model and its
application for still and video images. In Coloration
Technology, 30:77-92.
Madin, A. and Ziou, D. (2014). Color constancy for visual
compensation of projector displayed image. In Dis-
plays 35, 617.
Spitzer, H. and Semo, S. (2002). Color constancy: a bi-
ological model and its application for still and video
images. In Pattern Recognition, 35:1645-1659.
Stokes, M., Anderson, M., Shandrasekar, S., and Motta, R.
(1996). A standard default color space for the internet
- srgb. In Version 1.10.
West, G. and Brill., M. H. (1982). Necessary and sufficient
conditions for von kries chromatic adaptation to give
colour constancy. In J. Math. Biol, 15:249-258.
Wilkie, A. and Weidlich, A. (2009). A robust illumination
estimate for chromatic adaptation in rendered images.
In Eurographics Symposium on Rendering.
Content based Computational Chromatic Adaptation
49
