Person Re-identiﬁcation based on Human Query on Soft Biometrics

using SVM Regression

Athira Nambiar, Alexandre Bernardino and Jacinto C. Nascimento

Institute for Systems and Robotics, Instituto Superior T

ecnico,

Av. Rovisco Pais, 1, 1049-001, Lisbon, Portugal

Keywords:

Soft biometrics, Shape Context, SVM Regression, Re-identiﬁcation, Silhouettes, Retrieval, Surveillance.

Abstract:

We propose a novel methodology for person re-identiﬁcation (Re-ID) based on the biometric description of

the upper-torso region of the human body. The proposed methodology leverages soft biometrics via Support

Vector Regression (SVR) and Shape Context (SC) features obtained from the upper-torso silhouette of the

human body. First, mappings from the upper-torso Shape Context to soft biometrics are learned from virtual

avatars rendered by computer graphics engines, to circumvent the need for time consuming manual labelling

of human datasets. Second, it is possible to formulate a human query of a given suspect against a gallery of

previously stored soft biometrics. At this point, the proposed system is able to provide a ranked list of the

persons, based on the description given. Third, an extensive study on the different regression methodologies

to achieve the above mentioned mappings is carried out. We also conduct real time Re-ID experiments in an

existing Re-ID dataset, and promising results are reported.

1 INTRODUCTION

In order to re-identify a person in a video surveillance,

we usually rely on previously stored image/videos of

the person or a verbal description of its biometric fea-

tures. In this paper, we focus on the latter case via

soft-biometric descriptions. Soft biometrics are the

human characteristics providing categorical informa-

tion such as age, gender, height, weight, length of

arms and legs, skin/ hair color, gait and gestures, ac-

cent, etc. (Jain et al., 2004). In contrast to “hard” bio-

metrics, such as ﬁngerprint, retina, that encode unique

and permanent personal characteristics, soft biomet-

rics provide vague physical or behavioral information

which may not be permanent or distinctive. How-

ever, there are certain advantages that make soft bio-

metrics well suited to surveillance applications: they

are usually easier to capture from a distance or from

low quality data, and do not require cooperation from

the subjects. Since these features are human inter-

pretable, people can use them to refer to other people

in re-identiﬁcation (Re-ID) scenarios e.g., eyewitness

of the suspect in a criminal scene (long face, fat, bald

person).

With the arrival of sophisticated measurement sys-

tems such as 3D sensors (Kinect) and high deﬁni-

tion cameras, several applications of soft biomet-

rics for video surveillance were reported in the last

decade. (Barbosa et al., 2012) presented a set of 3D

soft biometric cues related to anthropometric mea-

surements, obtained from KINECT RGB-D sensors

and employed in person Re-ID. Many studies on gait

based person recognition and re-identiﬁcation were

reported in (Bedagkar-Gala and Shah, 2014), (Gof-

fredo et al., 2009) and (Nambiar et al., 2012). In (Le-

An. et al., 2013), new methods for improving the Re-

ID performance by re-ranking based on Soft biomet-

ric attributes are discussed. Some works addressed

the issue of person Re-ID based on human query as

well. (Dantcheva et al., 2010) proposed a BoSB bag

of soft biometric traits (e.g., facial and body soft bio-

metrics) for person Re-ID. In (Reid and Nixon, 2011)

a large number of manual annotations of comparative

biometric measurements was collected from numer-

ous human annotators. In (Denman et al., 2012), per-

son matching using semantic description is achieved

using size and colour cues.

Person retrieval based solely on biometrics

presents several challenges: (i) many people may

share similar biometrics; (ii) verbal descriptions are

qualitative and relative among individuals; (iii) it is

difﬁcult to bridge the semantic gap between human

descriptions and real measurements. In this work, we

explore new strategies to tackle these issues by link-

ing these human interpretations to those of machine

representations. With the aid of a machine learning

484

Nambiar, A., Bernardino, A. and Nascimento, J.

Person Re-identiﬁcation based on Human Query on Soft Biometrics using SVM Regression.

DOI: 10.5220/0005679404840492

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 484-492

ISBN: 978-989-758-175-5

technique (Regression), we ﬁnd the relationship be-

tween biometric features of a person and its com-

puter vision features – histograms of Shape Context

(SC) descriptors (Belongie et al., 2002) to encode the

upper-torso silhouette of the humans.

One of the main challenges to train regression

models is the availability of the ground truth biomet-

ric features. Due to the urge for a large datasets, hu-

man annotation of video sequences does not seem a

feasible approach. Instead, we propose the genera-

tion of a database of synthetic avatars, whose bod-

ily proportions can be manipulated easily. Regression

analysis is then achieved via SVM Regression.

With respect to works in the state-of-the-art, our

retrieval system using soft biometrics neither requires

very high image resolution, as for facial features in

(Dantcheva et al., 2010), nor laborious and plenti-

ful manual annotations over real world dataset as in

(Reid and Nixon, 2011). Also, in contrast to (Denman

et al., 2012) and (Dantcheva et al., 2010), our system

doesn’t consider the appearance cues such as clothing

colour, thus enabling towards long-term person Re-

ID. Hence, we propose a novel automatic person Re-

ID system solely based on biometric features, exploit-

ing regression models and modern computer graphics

technology.

The rest of the paper is organized as follows: The

system architecture is explained in Section 2. In Sec-

tion 3, the image features descriptors are explained.

Then, Section 4 explains the regression process we

carried out, including the generation of the dataset of

avatars and the basics of SVM regression. In Sec-

tion 5, the various experiments conducted and their

results are detailed along with a real world case study

of Person Re-ID. We summarize our work and enu-

merate some future work plans in Section 6.

2 SYSTEM ARCHITECTURE

The objective of our proposed system is to re-identify

the person purely based on semantic human descrip-

tions on his/her soft biometric features (BF) of the

upper torso, such as chest width, shape of the face,

neck size etc. We design our system in order to link

these human compliant soft biometric cues with those

of the machine interpretable computer vision features

extracted from people. So, whenever the human query

is provided, our system will provide the list of people

observed in the system with biometric features similar

to that query. Basically, there are two training phases

involved in our procedure. The ﬁrst one is for obtain-

ing the regression model and the second one is the

training for holistic Re-ID system.

Training Regression Model: To gather a large

enough set of data for regression, we generate avatars

in virtual reality based on groundtruth soft biometric

values, and extract the corresponding SC feature

descriptors. Then, regression analysis is carried

out to obtain the regression parameters. A pictorial

representation of the regression block is given in

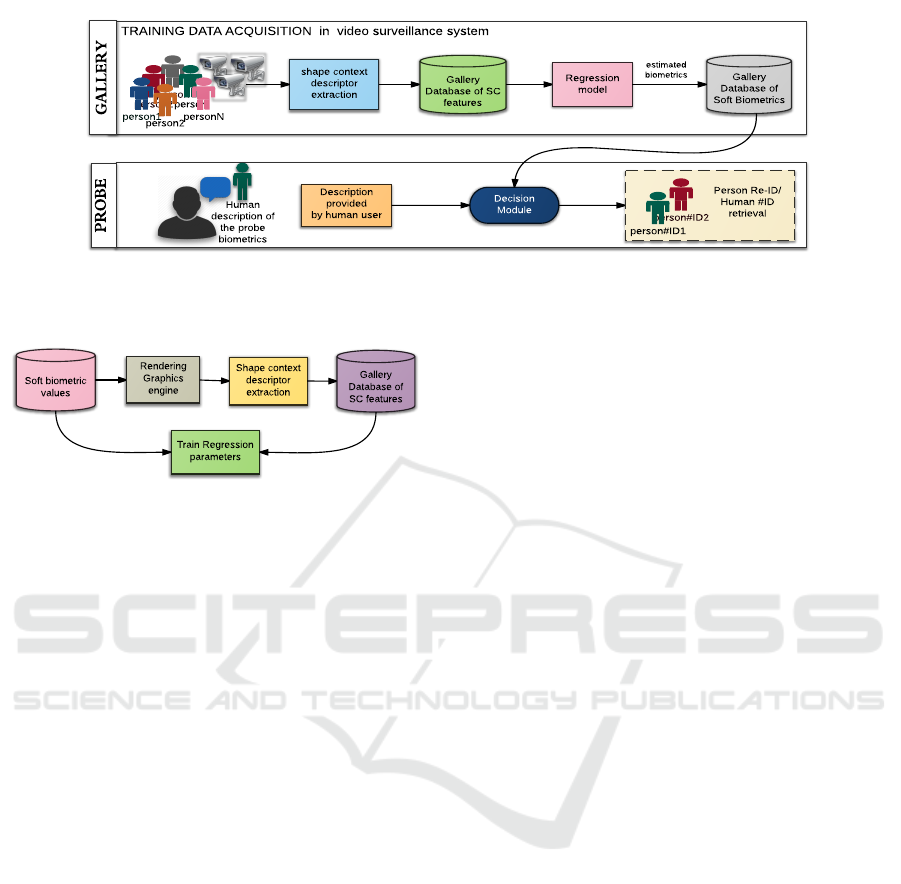
Fig. 2.

Training the Re-ID System: The general framework

of the proposed system is presented in Fig. 1. During

the training stage for the re-identiﬁcation, we acquire

the image data for all people appearing in the surveil-

lance scenario via a number of cameras situated at

various positions in the network. This set is denoted

as “Gallery”. Afterwards, we carry out the feature

extraction from the collected data. We leverage

Shape context (SC) descriptors for the extraction of

features of the upper torso of each person. These

extracted SC features are stored in a Gallery Database

of SC features. A regression block will process the

data on this set. As mentioned earlier, this block

divulges the relation of SC descriptors with soft

biometrics, and it estimates biometric feature (BF)

values corresponding to each sample. Hence, for

each Gallery image, the corresponding biometric

value is estimated and stored in the Gallery Database

of Soft Biometrics. This data is further processed and

a statistical analysis is generated among the whole

population and stored for later use.

Using the Re-ID System: Whenever a human probe

query (in terms of the biometric description of the

suspect) is entered in the system by an operator, the

Biometric gallery is revisited by the system. Based

on the statistical proﬁle of the whole biometric info

as well as the current query, the decision module will

determine the most appropriate category of the sus-

pect. Each category is identiﬁed via range of quartiles

in this statistical chart. More details are explained

later in Section 5.2. Since many people might have

similar semantic labels resulting in subject interfer-

ence, we propose that grouping them into classes with

similar traits could be the best technique to tackle

this scenario. Hence, the output of the system will

be a ranked list of persons that share the similar hu-

man compliant traits. By considering many biometric

cues, we can ﬁne tune the person to be re-identiﬁed.

This is a kind of pruning method, which normally the

security people do manually on receiving the human

queries; we do it here automatically.

Person Re-identiﬁcation based on Human Query on Soft Biometrics using SVM Regression

485

Gallery

Database of SC

features

Decision

Module

Regression

model

Gallery

Database of

Soft Biometrics

Description

provided

by human user

shape context

descriptor

extraction

TRAINING DATA ACQUISITION in video surveillance system

GALLERY

PROBE

person

person2

person1

person

person2

personN

Human

description of

the probe

biometrics

Person Re-ID/

Human #ID

retrieval

person#ID2

person#ID1

estimated

biometrics

Figure 1: The scheme presents the holistic framework of our human re-identiﬁcation (Re-ID) system. Gallery is the storage

of data collected in the training phase, and probe is a human description of the subject provided by a human operator such as

eyewitness statement in a criminal scene.

Soft biometric

values

Rendering

Graphics

engine

Shape context

descriptor

extraction

Gallery

Database of

SC features

Train Regression

parameters

Figure 2: Framework for training the Regression model.

3 IMAGE DESCRIPTORS

Silhouettes: Of the many different image descriptors

that could be used for feature extraction of the person,

we have chosen image silhouettes. Silhouettes have

a number of interesting properties: (i) they yield the

shape of the person which encodes soft biometric

traits such as lengths, curvatures and size ratios in the

human body; (ii) they are insensitive to the surface

attributes such as clothing colour and texture, thus

better for long term based person re-identiﬁcation;

(iii) they are basic image edge information and could

be extracted reliably using many techniques such as

background subtraction, gradient analysis, depth map

in 3D sensors, etc.

Shape Context: In this work, we use shape con-

text descriptors to encode the shape over a range of

scales. The original idea of Shape Context was de-

scribed in (Belongie et al., 2002). In order to com-

pute shape similarity, they introduced a new descrip-

tor called Shape Context which measures the distribu-

tion of points in a shape relative to each point in that

shape. The silhouette shape is thus encoded as a dis-

tribution in the 60-D shape context space, by encod-

ing the local edge pixels into log- polar bins of 12 an-

gular ×5 radial bins. Then, matching silhouettes is re-

duced to matching Shape context descriptors. This is

accomplished by bipartite graph matching technique

as explained in the original paper. In our previous

study (Nambiar et al., 2015), the feasibility of using

Shape context features for person re-identiﬁcation us-

ing SC matching is validated by employing Hungar-

ian algorithm as an instance of Bipartite graph match-

ing, and veriﬁed by achieving a higher performance

accuracy of 95% in virtual avatars and 92.5% in real

imagery.

4 REGRESSION ANALYSIS

We leverage recent work on Support Vector Regres-

sion (SVR) to test linear as well as nonlinear models

on the ability to predict biometric features from im-

age data. A detailed explanation of our experimen-

tal dataset, SVM regression, the choice of basis, meta

parameters and the cross validation strategies are pro-

vided in this section.

4.1 Database of Generic Avatars

For the learning phase of the regression, we need to

have a benchmark dataset with the image descriptors

and the corresponding soft biometric information. To

collect these information by manually annotating on a

large real world human population is not only a very

strenuous task, but also prone to segmentation errors.

Thus, we simulated a large number of virtual silhou-

ettes using the graphics engine Unity3D

, with the

standard avatars viz. Male character pack and female

character pack (shown in Fig. 3) from Mixamo 3D

character animation service, as the baseline avatars.

Then the rest of the avatars were created by impos-

ing variations to the biometric features with respect

to these standard models, as explained in (Nambiar

et al., 2015).

For the standard avatars models, we assumed a

unitary scale factor of each biometric measurement

(see Fig. 4(a)). The soft biometric parametrization

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

486

Figure 3: Six standard avatars used in the synthetic platform

for the generation of large dataset by changing the biomet-

ric features. We make use of only the upper-torso region

including head, shoulder and chest.

imposed for simulating the generic avatar population

is shown in Table 1, where each value corresponds

to the scale applied to the standard model counterpart

of that anthropometric measurement. These scale pa-

rameters were deﬁned by analysing the variability in

real world human population. Fig. 4 shows an ex-

ample of the different virtual avatar samples gener-

ated out of a single basic standard avatar, by changing

each biometric feature individually. So, altogether 9

variations were generated out of each of the 6 stan-

dard avatars. Then, we executed walking animations

and captured random 4 frames for each person which

resembled the video surveillance image acquisition.

Thus we created our Generic avatar dataset consisted

of 216 images.

(a) (b) (c) (d) (e)

(f) (g) (h) (i)

Figure 4: The nine variations of biometrics simulated in the

generic avatars. Only the upper torso region is shown since

it is the region of our interest. Please refer to Table 1 for

measurement details.

4.2 Dataset for Regression

Let the regression be carried out from an input space

of dimension IR

to an output space of dimension IR.

Each element in the input space is a feature vector of

size p × 1. i.e. x =



,··· , x



. We collect n such

samples and represent them as a matrix X ∈ IR

n×p

X = [x

| · · · | x

]

(1)

Each row in the X matrix represents a feature vec-

tor corresponding to the n’th sample in the dataset.

We collect the response variables y

corresponding to

Table 1: Chart showing the soft biometric scale factors for

the simulated avatar versions in Fig. 4. Values highlighted

in bold characters in each row represents the modiﬁcation

imposed for that particular avatar.

Avatar

Index

Neckness

(N)

Chestsize

(C)

Bodysize

(B)

Head-

length

(HL)

Head-

width

(HW)

Human

description

label

(a) 100% 100% 100% 100% 100% Standard

(b) 200% 100% 100% 100% 100% Large neck

neck

(d) 100% 200% 100% 100% 100% Large chest

(e) 100% 300% 100% 100% 100% Very large

chest

(f) 100% 100% 50% 100% 100% Thin body

(g) 100% 100% 200% 100% 100% Fat body

(h) 100% 100% 100% 125% 100% Long head

(i) 100% 100% 100% 100% 125% Wide head

each input sample x

and represent them as a vector

y ∈ IR

n×1

, as follows:

y =



...,y



(2)

In our case, X contains the input SC descriptors and y

holds the Biometrics values of the simulated avatars.

We have 216 avatar samples corresponding to 4 dif-

ferent views of each of the 54 different avatars. The

Shape Descriptors are composed of 40 points across

the edge of the upper torso silhouette, each with 60D

shape context descriptor and thus producing a 2400

dimensional feature vector corresponding to a person,

i.e., input matrix X is of dimension IR

216×2400

. The

output biometric consists of 5 biometrics say, BF= (N,

C, B, HL, HW). In our experiment, we conduct regres-

sion analysis individually for each of the biometrics in

the set BF. More speciﬁcally, y in equation (2) will be

a vector of dimension 216 containing a given biomet-

ric feature for all the avatars. Thus, each regression

analysis will be from IR

216×2400

matrix to IR

216

vec-

tor.

4.3 Support Vector Regression

Support Vector Machines (Cortes and Vapnik, 1995)

can be applied not only to classiﬁcation problems but

also to the case of regression (Smola and Schlkopf,

1998), (Chapelle and V., 1999).

Training the original SVR as per (Smola. and

Schlkopf., 2004) is mentioned below. Suppose the

training data {(x

),....(x

)} ⊂ X × R where, X

denotes the space of the input patterns. (e.g. X = R

)

Consider linear functions f, taking the form

f(x) =< w,x > +b, w ∈ X ,b ∈ R (3)

where < .,. > denotes the dot product in X . Solv-

ing this convex optimization problem yields the

formulation below. In order to cope with the in-

feasibile constraints of the optimization problem,

slack variables ξ

,ξ

∗

are introduced to perform the

minimization of the following cost function:

Person Re-identiﬁcation based on Human Query on Soft Biometrics using SVM Regression

487

minimize

||w||

∑

i=1

(ξ

+ ξ

∗

s.t.











− < w,x

> −b ≤ ε + ξ

< w,x

> +b − y

≤ ε + ξ

∗

,ξ

∗

≥ 0

(4)

The constant C > 0 determines the trade-off be-

tween the ﬂatness of such a function f and the amount

up to which deviations larger than ε are tolerated.

To extend this towards nonlinear functions, the main

strategy is dual formulation. Hence, the optimization

problem could be transformed into a dual problem

and its solution is given by:

f (x) =

∑

i=1

(α

−α

∗

)K(x

)+b, s.t.,

(

0 ≤ α

∗

≤ C,

0 ≤ α

≤ C

(5)

where, α

,α

∗

are the dual variables and K(x

) is the

Kernel function.

4.4 Meta Parameters

The performance of Support Vector Regression

(SVR) depends on a good setting of meta parameters.

We tested two kinds of regression kernels: (i) Linear

Kernels

K(x

) ≡< x

> (6)

which implies that the regressor is linear with respect

to the input vector ; (ii) Radial basis kernel, where

K(x

) ≡ exp(−γ||x

− x

), γ =

2σ

(7)

To determine which values of C and γ are best

for our problem we use grid search with cross-

validation. We used logarithmic grids both for C (C

-15

-13

.....,2

) and γ (γ=2

-15

-13

.....,2

). For each

pair, we measure the prediction error (Mean Square

Error- MSE) and the lowest MSE corresponds to the

best parameters. We conducted two different cross

validation techniques:

(a) K-fold Cross Validation: We ﬁrst divide the

training set into k subsets of equal size. Sequentially,

one subset is tested using the regressor trained on the

remaining k-1 subsets. This rotation estimation will

go on k times, and ﬁnally, the prediction errors over k

folds will be averaged to produce a single estimation.

(b) Stratiﬁed K-fold Cross Validation: In strati-

ﬁed k-fold cross validation, the folds are selected such

that each set contains approximately the same per-

centage of samples of each target class as the com-

plete set. “Stratiﬁed” cross-validation is a simple vari-

ant of classical k fold cross-validation. It basically

makes sure that we choose a division that has approx-

imately the right representation of class values in each

of the folds. It helps reduce the variance in the esti-

mate a little bit more.

After the cross validation is done, we will get a

single estimation of the measure of ﬁt viz., the aver-

age MSE Train and the corresponding meta parame-

ters. Based on this model, we train the whole system

so that whenever the test data enters, it will estimate

the output variables.

5 EXPERIMENTAL RESULTS

We conducted experiments using the database of 54

avatars, with 4 samples each. The regression analysis

is conducted from the input space of IR

2400

to out-

put space of IR. Among the output biometrics to be

estimated say, BF= (N, C, B, HL, HW), we perform

regression analysis individually for each of them i.e.,

we regress the scalar estimate of each biometric from

a 2400-D shape context vector. In our experiments,

we selected 2 random avatars, each with 4 samples

(total 8 samples), as the test set and the remaining 52

people, each with 4 samples as the training set (total

208 samples).

5.1 Regressor Performance

We conducted 6 different experiments on our data,

over different kernels as well as different cross valida-

tion schemes. Out of these experiments, we report the

Mean Squared error viz., MSE Train and MSE Test in

both the training and test sets, as well as the best meta

parameters (the ones leading to the least MSE Train).

Table 2 summarizes the test and train set perfor-

mances of the various regression methods studied on

a single biometric feature (Neckness). Linear and ker-

nelized basis versions were tested with different cross

validation schemes, at manual and optimal regularizer

settings. MSE

Train corresponds to the Mean Square

Error obtained for the training set obtained via Cross

validation, and the MSE Test is the the Mean Square

Error obtained for the test set. In the default param-

eter setting, the default meta parameters are activated

(C=1, γ=1/num features, ε=0.1), whereas in exhaus-

tive grid search, the optimal values of meta param-

eters are selected as the pair of (C,γ) producing the

least MSE Train in the training set. A sample grid

search selection of optimal meta parameters for Exp.5

(in Table 2) is depicted in Fig. 5(a).

In order to verify the repeatability/consistency of

the measure of ﬁt, we executed 10 runs of random tri-

als (with Cross validation of 2 fold) for the same bio-

metric. The boxplot representation of the variability

of regression performance in terms of Mean Squared

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

488

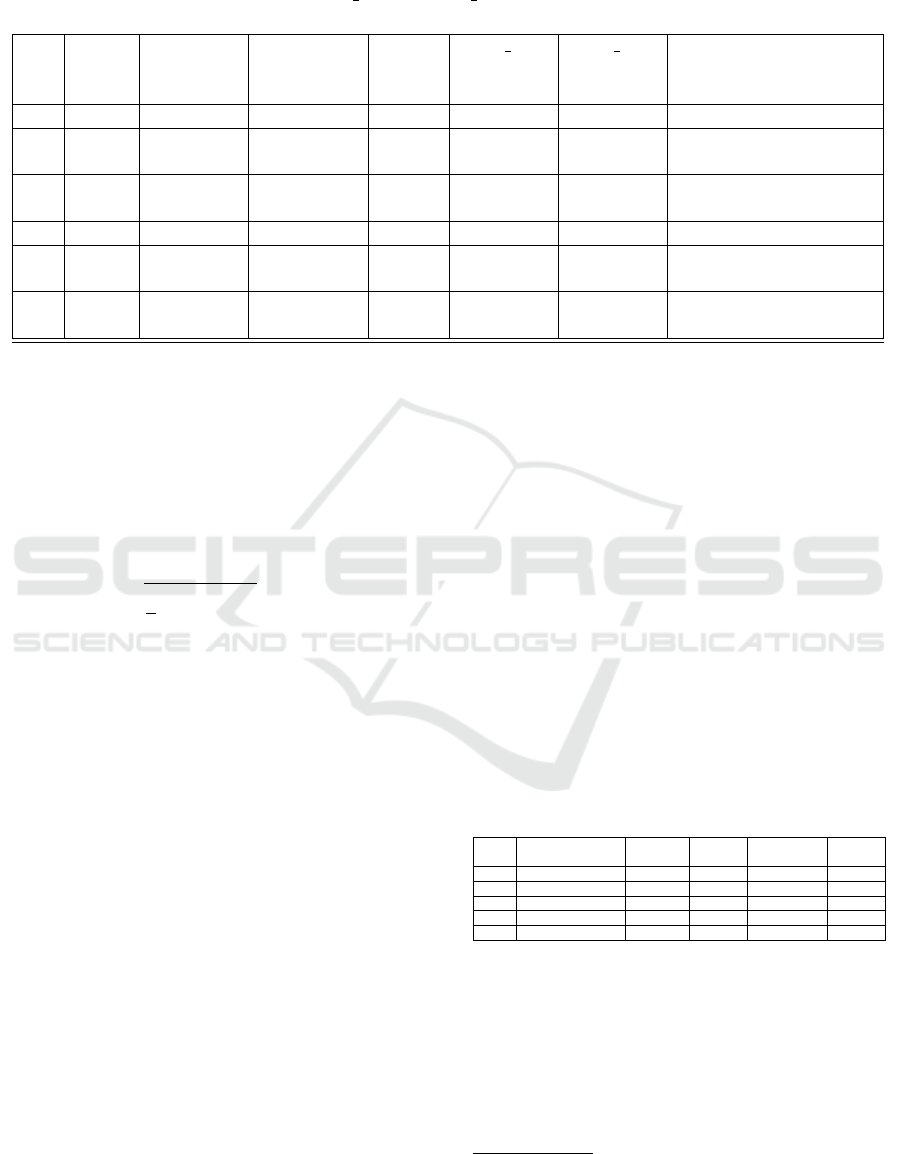
Table 2: Performance of Linear and Nonlinear regression models studied in this work on biometric1 (Neckness), for different

parameter settings as well as cross validation schemes. The experimental results over 2-fold as well as 4-fold cross validation

settings are shown below. Least values of MSE Train and MSE Test are shown in bold characters and the second least in

italics.

Exp Kernel Parameter

Setting

Cross

validation

(CV)

No.

of CV

fold

MSE Train MSE Test Meta parameter

(1) Linear Default - - 0.0100 1207.5 default

(2) Linear Gridsearch Stratiﬁed 2 17.2178 991.1524

C= 0.5; γ= 9.5367e-07

4 94.1696 1319.5

(3) Linear Gridsearch K-fold 2 95.24996 1347.6

C= 0.25; γ=3.0518e-05

4 468.1726 2986.8

(4) RBF Default - - 4726.4 19211 default

(5) RBF Gridsearch Stratiﬁed 2 0.3974 985.2449

C=1024; γ=0.00024414

4 0.00010061 1240.0

(6) RBF Gridsearch K-fold 2 41.5721 1033.1433

C=1024; γ= 4.8828e-4

4 0.5671 1924.0950

Error for both train and test sets are shown in Fig. 5(b)

and Fig. 5(c) respectively.

Next, we try to extend the case studies conducted

on a single biometric feature (Neckness), over all the

5 biometrics say (Neckness, Chest width, Body size,

Head length and Head width). Since the ranges of

the various biometrics features are different, we use

the normalized root mean square error NRMSE for the

evaluation of our regressor.

NRMSE =

∑

i=1

( ˆy

− y

)

/(y

max

− y

min

) (8)

The visualization of the NRMSE values for all the

regression methods over all biometrics under consid-

eration, is given in Fig. 6.

Following are the main ﬁndings from our experi-

ments conducted above:

1) Grid-search on meta parameters can ﬁne tune

the measure of ﬁt, and thus the optimal nonlinear

experiments outperforms the others in all the cases:

Our experiments with linear function and RBF kernel

show that kernelization gives a slight improvement in

performance. For e.g., referring to Table 2 as well as

Fig. 6 we can observe that the default values of param-

eters produce very bad results for RBF kernel (worst

results among all) whereas the grid search of the meta

parameters could ﬁne tune the performance. Simi-

larly, applying grid search in linear regression also

can reduce the estimation error to some extent.

2) We observed a nearly Linear Relationship be-

tween SC descriptors and the corresponding Biomet-

rics; In other words, Linear Regression lies very close

to cross validated nonlinear regression modalities: In

the boxplots of Fig. 5 as well as the barplot in Fig. 6,

we could observe that linear kernels as well as the

cross-validated RBF kernel produced more or less the

same range of estimation errors. Also in terms of con-

sistency of estimation errors also similar results are

observed. So we conclude that, the nonlinear kernel-

ization could bring only a small advantage over purely

linear regression against our descriptor set. This intu-

itively indicates that there exists a nearly linear re-

lationship between the Shape Context descriptor and

the corresponding Biometrics.

3) Cross Validation Inﬂuences in the System Per-

formance: Among two types of cross validation

schemes we applied on our data, we could observe

that Stratiﬁed k-fold CV outperforms the k-fold CV,

in terms of accuracy and consistency. After learning

the relationship among the Shape Context descriptors

and the Soft Biometrics, we built the best regression

model for our Re-ID system using Nonlinear regres-

sion with RBF stratiﬁed CV.

Table 3: Chart showing the meta parameters settings of RBF

for the best regression performance.

Index Biometric Kernel

type(t)

Cost

(C)

Gamma

(γ)

Epsilon

(ε)

1 Neckness(N) RBF 1024 0.00024414 0.01

2 Chestsize(C) RBF 1024 0.00048828 0.01

3 Bodysize(B) RBF 128 0.00024414 0.01

4 Headlength(HL) RBF 64 0.00048828 0.01

5 Headwidth(HW) RBF 64 0.00048828 0.01

5.2 Person Re-ID in Real World

After pondering various regressor models on our

Virtual Generic avatar dataset, we employ it in a real

world dataset for person re-identiﬁcation. In this

work we conducted a pilot study using 20 people

from RGB-D Person re-identiﬁcation Dataset

. A

http://www.iit.it/en/datasets-and-code/datasets/rgbdid.ht

Person Re-identiﬁcation based on Human Query on Soft Biometrics using SVM Regression

489

(a) (b) (c)

Figure 5: (a) Contour and Surface plots of the MSE Train distribution for various C and γ meta parameters. Blue corresponds

to lowest MSE Train. log

(C)= 10 and log

(γ)= -12 produces the least prediction error (lowest MSE Train) (b) MSE for the

trainset (MSE Train) over 10 random runs (c) MSE for the testset (MSE Test) over 10 random runs.

Figure 6: A summary of our various regressors’ perfor-

mance on different biometrics estimation.

(a)

#P1

(b)

#P2

(c)

#P3

(d)

#P4

(e)

#P5

(f)

#P6

(g)

#P7

(h)

#P8

Figure 7: A sample real world dataset for the retrieval test

based on human queries on biometric info.

subset of our real world dataset is given in Fig. 7.

Characterising the Gallery Soft-Biometrics: Refer-

ring to our proposed system in Fig. 1, the image de-

scriptors for each person in the dataset are used in

the training phase of Re-ID system in terms of SC

descriptors of upper torso, and stored in the system

gallery. Afterwards, these SC descriptors are pro-

cessed using the Regression block designed as per Ta-

ble 3, and the corresponding biometric estimation for

each individual is made. Finally, a statistical distri-

bution analysis of the stored biometrics is carried out

in the same module and stored along with the biomet-

ric values, for later use. This statistical proﬁle is the

distribution chart of each biometric values observed

among the whole population. The statistical analysis

of estimated biometric values among our real human

dataset is presented in Fig. 8.

Figure 8: Biometric data distribution predicted for the real

dataset, using the regression model learned using simulated

avatars.

We can observe a range of variances along the

biometrics estimated among the dataset. The distri-

bution of Neckness ranges between 100% to 130% of

the trained simulator models. The parameter distri-

bution of chestsize ranges between 120% and 230%,

with median close to 190%. Bodysize, Headwidth

and Headlength are centered near the 100%, and have

lower variances. Largest variance is observed for

Chest size and least variances are observed for head

length and head width. It is important to have certain

biometrics with large variance in the population in

order to avoid the problem of subject interference

and to improve the distinctiveness among people.

They act as the most discriminative features. In our

case, Chest size is the most discriminative biometric

feature.

Re-identiﬁcation from Verbal Queries: When the

query probe in terms of description of the human bio-

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

490

metric is entered into the system (for instance, person

with large chest and short neck), our system will anal-

yse the biometric distribution of the training samples

as in Fig. 8. The most acclaimed semantic categories

are interpreted in terms of data ranges in this distribu-

tion proﬁle as follows: Short (S-less than lower quar-

tile), Medium (M-lower quartile to upper quartile) and

Large (L-above upper quartile). Then, the biometric

description in the query is compared against the afore-

mentioned semantic categories, and the valid cate-

gory of interest is retrieved. As an example, we will

select the list of people with the biometric traits of

chestsize≥200% (more than the upper quartile of bio-

metric C) and neckness≤110% (less than the lower

quartile of biometric N). In our case study of real

dataset in Fig.7, person ID’s (f) #P6 and (h) #P8 were

correctly re-identiﬁed under the query made, and their

corresponding frames in the camera network were re-

trieved.

6 CONCLUSIONS

In this work, we presented a novel method for re-

identifying people in a video surveillance system by

means of verbal queries describing human compliant

soft biometric labels. This was done by exploiting

regression techniques associating Shape context fea-

tures to Soft biometric values. In order to provide

the best model for the Regression analysis, we con-

ducted an extensive study on the impact of various re-

gression schemes as well as cross validation schemes

on Shape Context- biometrics pairs of our simulated

dataset of Virtual reality avatars. We observed that the

grid search for the best meta parameterized model can

ﬁne tune the system for the best performance. In our

experiments nonlinear kernel (RBF) basis with strati-

ﬁed Cross validation excels in performance compared

to all the other schemes. Interestingly, linear regres-

sion models are also found to provide good and fast

results. This gives us the intuition that the correla-

tion between the SC and biometrics are nearly linear.

We trained our system with the best regression model

RBF kernel with Stratiﬁed cross validation. Using the

meta parameters obtained, we experimented for the

biometric estimation not only in the simulated plat-

form, but also in real imagery. We showed that, based

on the statistical distribution of these biometrics, our

system could retrieve promising results for person re-

identiﬁcation based on human query. In the future

work, we plan to extrapolate our proposed method-

ology from upper torso towards full human body i.e.

to extract the features over full body and to exploit

a large set of soft biometrics deﬁning the full body

speciﬁcations such as height, weight, lengths of hands

and legs, waist width etc. In addition to that, we also

intend to combine other biometric cues such as gait,

face etc. along with the current shape features using

multi-modal fusion techniques.

ACKNOWLEDGEMENTS

This work was partially supported by the

FCT projects [UID/EEA/50009/2013], AHA

CMUP-ERI/HCI/0046/2013, doctoral grant

[SFRH/BD/97258/2013] and by European Com-

mission project POETICON++ (FP7-ICT-288382).

REFERENCES

Barbosa, B. I., Cristani, M., Del Bue, A., Bazzani, L., and

Murino, V. (2012). Re-identiﬁcation with rgb-d sen-

sors. In Computer VisionECCV.

Bedagkar-Gala, A. and Shah, S. (2014). Gait-assisted per-

son re-identiﬁcation in wide area surveillance. In

Computer Vision - ACCV 2014 Workshops, Singapore.

Belongie, S., Malik, J., and Puzicha, J. (2002). Shape

matching and object recognition using shape contexts.

IEEE Transactions on PAMI.

Chapelle, V. and V., V. (1999). Model selection for support

vector machines. In Advances in Neural Information

Processing Systems, Vol 12.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine Learning.

Dantcheva, A., Velardo, C., D’angelo, A., Dugelay, and

Jean-Luc (2010). Bag of soft biometrics for person

identiﬁcation: New trends and challenges. Mutimedia

Tools and Applications, Springer.

Denman, S., Halstead, M., Bialkowski, A., Fookes, C., and

Sridharan, S. (2012). Can you describe him for me? a

technique for semantic person search in video. In Dig-

ital Image Computing : Techniques and Applications.

Goffredo, M., Bouchrika, I., Carter, J., and Nixon, M.

(2009). Performance analysis for automated gait ex-

traction and recognition in multi-camera surveillance.

Journal of Multimedia Tools and Application.

Jain, A. K., Dass, S. C., and Nandakumar, K. (2004). Can

soft biometric traits assist user recognition? In Pro-

ceedings of SPIE.

Le-An., Chen, X., Kafai, M., Yang, S., and Bhanu, B.

(2013). Improving person re-identiﬁcation by soft bio-

metrics based reranking. In ACM/IEEE International

Conference on Distributed Smart Cameras (ICDSC).

Nambiar, A., Bernardino, A., and Nascimento, J. (2015).

Shape context for soft biometrics in person re-

identiﬁcation and database retrieval. PRLetters.

Nambiar, A. M., Correia, P. L., and Soares, L. D. (2012).

Frontal gait recognition combining 2d and 3d data. In

Proceedings of the on Multimedia and Security.

Person Re-identiﬁcation based on Human Query on Soft Biometrics using SVM Regression

491

Reid, D. and Nixon, M. (2011). Using comparative human

descriptions for soft biometrics. In In The ﬁrst Inter-

national Joint Conference on Biometrics.

Smola, A. and Schlkopf, B. (1998). A tutorial on support

vector regression. NeuroCOLT Technical Report NC-

TR-98-030, Royal Holloway College, UK.

Smola., A. and Schlkopf., B. (2004). A tutorial on support

vector regression. In Statistics and Computing 14 (3).

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

492