Angular Uncertainty Reﬁnement and Image Reconstruction

Improvement in Cryo-electron Tomography

Hmida Rojbani

1,2

Etienne Baudrier

, Benoˆıt Naegel

, Lo¨ıc Mazo

and Atef Hamouda

University of Strasbourg, 67412, Illkirch CEDEX, France

Faculty of Science of Tunis, University El-Manar, 2092, El Manar Tunis, Tunisia

eywords:

Electron Tomography, 3D Structures, Tilt Angles, Angular Uncertainty, Optimization, Conjugate Gradient.

Abstract:

In the ﬁeld of cryo-electron tomography (cryo-ET), numerous approaches have been proposed to tackle the

difﬁculties of the three-dimensional reconstruction problem. And that, in order to cope with (1) the missing

and noisy data from the collected projections, (2) errors in projection images due to acquisition problems, (3)

the capacity of processing large data sets and parameterizing the contrast function of the electron microscopy.

In this paper, we present a novel approach for dealing with angular uncertainty in cryo-ET. To accomplish this

task we propose a cost function and with the use of the nonlinear version of the optimization algorithm called

Conjugate Gradient, we minimize it. We test the efﬁciency of our algorithm with both simulated and real data.

1 INTRODUCTION

For a better understanding of the biological cells, sci-

entists use electron microscopy to investigate their in-

ner structures. The cryo-ET offers the possibility to

reconstruct the three dimensional (3D) volume of a

cell slice. The cryo-ET principle is to acquire two

dimensional (2D) projections with the Transmission

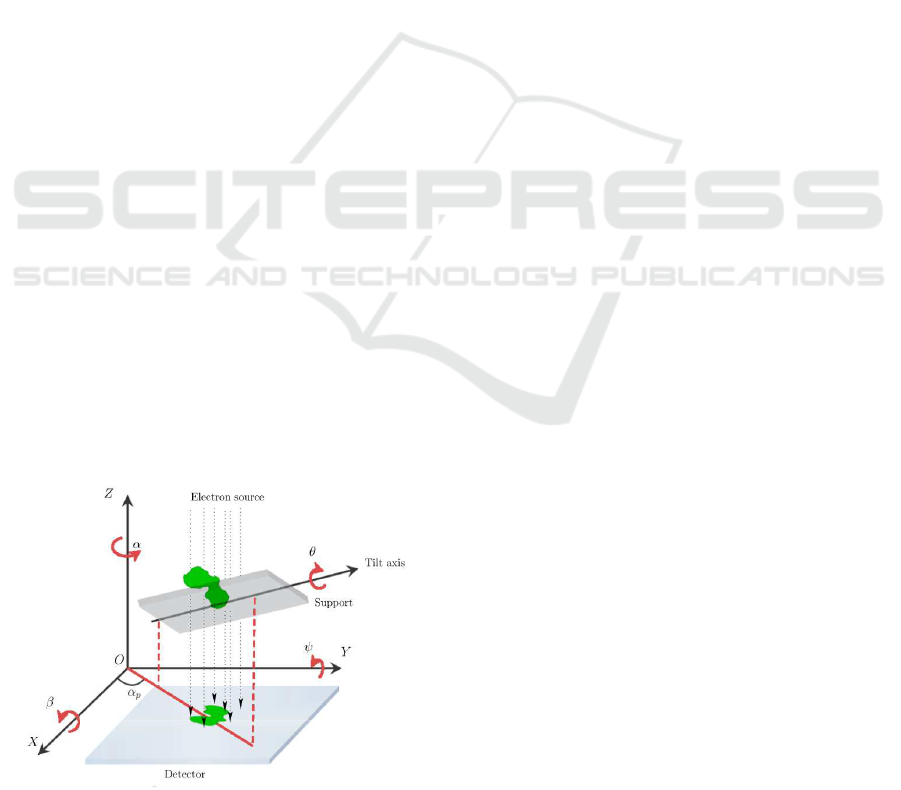
Electron Microscope (TEM) by tilting the sample

around an axis (cf. Figure 1). The tilting range is

[−70

◦

, 70

◦

] with steps between 2

◦

and 5

◦

. Then the

projection angles are known and are used in the re-

construction of the 3D sample. Figure 2 presents the

four different steps of cryo-ET.

Figure 1: Transmission electron microscopy acquisition

mechanism.

Nevertheless, there are several limits to the reso-

lution of the reconstruction: the missing data corre-

sponding to the uncovered projection space, the low

electron dose used during the acquisition to minimize

the weight of radiation damage (Egerton et al., 2004),

the thickness of the ice used in the sample ﬁxation

that affects also the ﬁnal reconstructed volume reso-

lution (Stagg et al., 2006) and the error made on the

projection parameters. The missing data, the electron

dose and the ice thickness are an acquisition phase

problem that we cannot correct them directly in our

work, but we try to minimize their effect on the re-

construct results. The classical reconstruction pro-

cess involves as a ﬁrst step an image alignment pro-

cess. The two well common alignment techniques are

(Frank, 2006): (1) marker tracking, where gold par-

ticles are implanted into the samples before the ac-

quisition of the images and then the calculation based

on these markers is used to align the images (Brandt

and Ziese, 2006), (Sorzano et al., 2009); (2) cross-

correlation methods, where alignment is carried out

by the cross-correlation calculation between each suc-

cessive couple of images (Zheng et al., 2010).

The second step of the cryo-ET is the 3D re-

construction. Numerous reconstruction methods are

used in cryo-ET, mainly belonging to two families.

First, the analytic family, with methods as ﬁltered

back-projection or direct Fourier inversion, imple-

mented in Fourier’s space (Penczek, 2010). The sec-

ond family is the algebraic family, with iterative real-

Rojbani, H., Baudrier, É., Naegel, B., Mazo, L. and Hamouda, A.

Angular Uncertainty Reﬁnement and Image Reconstruction Improvement in Cryo-electron Tomography.

DOI: 10.5220/0005680600940100

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 96-102

ISBN: 978-989-758-175-5

space methods such as ART (Gordon et al., 1970) or

SIRT (Gilbert, 1972).

Besides the reconstruction difﬁculties, the acqui-

sition process rises different type of problems such

as the specimen movement (translation, rotation) over

the carbon support especially when the tilting reaches

the highest values, the blur caused by the Contrast

Transfer Function (CTF), and the uncertainty on the

angular information due to mechanical imprecision of

the microscope (Colliex, 1998). All these problems

affect the quality of resolution of the reconstructed

object. Many approaches are proposed to overcome

all this mentioned problems except for the angular

uncertainty, due to the fact that the resolution of the

reconstruction is mediocre, so the angular uncertainty

does not have the effect over it. Now days, and due to

the improvement of the reconstruction techniques, the

resolution become important especially when we aim

to reconstruct and locate small particles such as ribo-

some and nucleosomes. Treating the angular uncer-

tainty will push as forward to a better reconstruction

resolution.

We begin in our work by concentrating on the

angular uncertainty problem, which we prove in our

tests that even a slight change in the set of angles use

in the reconstruction has its affect over the accuracy

of the resolution of the reconstructed 3D volume. Our

approach is based on optimization problem where we

use a cost function has the set of angles as parameters

to be minimized. To gain more accuracy we include

also the reconstructed object as parameters into the

function. Using the two sets of parameters simulta-

neously in our approach provides more accurate re-

sults than optimizing the angular uncertainty and the

reconstructed object separately.

Figure 2: Different Steps of cryo-ET.

2 RELATED WORK

In recent years, the use of simultaneous optimization

is increased in many ﬁelds. One of those ﬁelds is

the alignment phase in the reconstruction. For exam-

ple, in the ﬁeld of the singular particles reconstruc-

tion, a large set of small projections used in the re-

construction of an object are from unknown orien-

tations. Thus, to improve the estimation of the un-

known projection orientations, Yang et al. (Yang

et al., 2005) proposed to use a Quasi-Newton opti-

mization based algorithm to minimize a cost function

between the projection angles and the reconstructed

3D object starting from a rough reconstruction.

In cryo-ET, the context is different: the data is a

small set of large projections with known tilt angles.

However, this tilt angles can be erroneous due to the

malfunction of the tilt mechanism of the object holder

in the TEM. In this ﬁeld, Tran et al. (Tran et al.,

2013) proposed a hierarchical method to correct the

reconstruction and the alignment problems in alter-

nating way. They treat the transformation parameters

(translation, rotation, scale). Inspiring from the cross-

correlation method of alignment, they begin by ﬁnd-

ing the ﬁrst set of transformationparameters by an op-

timization between each successive pair of projection

images. After that, a ﬁrst reconstruction is applied

followed by reﬁnement of the set of transformation. If

the method has not yet converged,they raise a new re-

construction. Infact, the reconstruction is based on an

optimization between the actual projections and the

resulting projections of the reconstructed object. In

the same way, the phase of reﬁnement of transforma-

tion parameters represents an optimization between

the processing parameters found from the current pro-

jections and those of the previous iteration.

We propose in our work to optimize the recon-

structed object and the transformation parameters si-

multaneously at the same level. In addition, we take

into account the error of the angular uncertainty of

projection. Indeed, we make the correction on the

reconstructed object itself, instead of those made on

projections. The idea is to try for each projection ori-

entation used to reproduce the same projection pro-

vided by the TEM. In this paper, we only present our

work for the reﬁnement of the projection angles and

the reconstructed object.

The rest of the paper is structured as follows: in

Section 3, the projection algebraic model of the ac-

quisition is given; in Section 4, the proposed approach

is detailed and the associated cost function is deﬁned;

the results are shown and discussed in Section 5. Fi-

nally, we summarize and give some perspectives.

Angular Uncertainty Reﬁnement and Image Reconstruction Improvement in Cryo-electron Tomography

3 PROJECTION ALGEBRAIC

MODEL

In the cryo-ET, The reconstruction is three-

dimensional problem, but in the section we will

give a general n-dimensional presentation for the

problem. To see the reconstruction problem as an

algebraic model, we must change the reconstructed

volume f and the projections images p

to their

respective vectors forms.

Let f be the vector representationof n-dimensional

image f, f = (f

, f

, . . . , f

)

. N is the number of vox-

els of f, in other words N = Π

d=1

, where N

is the

size of f in the dimension d.

Let p

= (p

, p

, . . . , p

)

is the vector represen-

tation of the n−1-dimensional projection image p

the image f according to the orientation θ

. M is the

number of pixels of p, in other words M = Π

n−1

d=1

where M

is the size of p

in the dimension d.

In fact, p is an element of a bigger vector P,

which contains all the elements of the S projec-

tions images. S is the numbers of the angles used

in the tilting process. We can assemble these an-

gles in a set called Θ, and then we have P =

, p

, . . . , p

), ∀θ

∈ Θ.

We deﬁne the relation between the projection vec-

tor P and the image vector f as:

P = Wf, (1)

Which can be seen also as :

= W

f, (2)

Thereby, the projection problem is modeled as an

equation system whose matrix W

is sparse. The ma-

trix W

holds the coefﬁcients of the projections ac-

cording to the angle θ

. In fact, each line of this matrix

describes one of the projection lines passing throws

the image. Many methods are proposed to calculate

this matrix such as ”voxel driven” and ”ray driven”

(Joseph, 1982). However, in our work, the calcula-

tion of W

is based on the ”distance driven” method

proposed by (Man and Basu, 2004). Note that the non

null coefﬁcients change when θ

changes but the ma-

trix W

remains sparse. The equation (2) cannot be

straightly inversed. Then we propose thereafter a re-

constructed volume reﬁnement method that simulta-

neously acts on the reconstructed volume and the tilt

angles.

4 PROPOSED APPROACH

When we investigate the reconstruction problem, we

ﬁnd that the only real data that we have it is the pro-

jections images and a set of uncertain angles of pro-

jection. Hence, the idea to create a function that can

calculate the difference or we can call it also the dis-

tance between the real projection data and the projec-

tion data found after re-projecting the reconstructed

volume according to the current set of angles. Thus,

by reﬁning these two, we can assure having a much

accurate reconstructed objet.

We begin by deﬁning the cost function C , which

presents the Euclidian distance between the real set of

projection data Π and the re-projection data from the

reconstructed object P, so we have :

C (f, Θ) =

kΠ − Pk

∑

i=1

kπ

− p

(3)

This equation can be developed to :

C (f, Θ) =

∑

i=1

∑

j=1

(π

− p

)

(4)

∑

i=1

∑

j=1

(π

−

∑

k=1

, j

)

(5)

where w

, j

is the projection coefﬁcient of the k-th

pixel by the j-th projection line according to the θ

The cost function C depends on three parameters,

the actual projections, the current reconstructed vol-

ume and the current tilt angles.

We use the square in the equation (3) to ensure the

positivity of the function. The similarity between the

two types of projections reaches its maximum when

the function C reaches its minimum. In this case, the

solution set of our problem (

Θ) is :

(

Θ) = argmin C (f, Θ) (6)

The equation (6) is convex in f (due to the using of

a quadratic sum) and Θ is close to the solution by hy-

pothesis . We can therefore assume that in this case,

the optimization problem of Eq. (6) is convex. More-

over, it is plain that the cost function C is not linear

according to (f, Θ). Thus, we have to use a non-linear

minimization algorithm. Among the knowndetermin-

istic optimization algorithms mentioned in the litera-

ture (Nocedal and Wright, 2006), we chose the non-

linear version of the Conjugate Gradient (CG) algo-

rithm (Dai and Yuan, 1999). The CG method is the

most prominent iterative method for solving sparse

systems of equations. We preferred this algorithm for

its convergence rate, its simple implementation and

since it appeals only to the ﬁrst order derivative.

The steps below constitute one of the CG itera-

tion of movement along a conjugate direction d

. The

algorithm starts by initializing d

= g

= −∇C (χ

)

(Dai and Yuan, 1999), then :

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

• ﬁnd α

the length of the descent step that mini-

mizes C (χ

+ α

• χ

i+1

= χ

+ α

• g

i+1

= −∇C (χ

i+1

• β

= max{

i+1

−g

)

, 0},

• updating the conjugate direction d

i+1

= g

i+1

The ﬁrst step to use the CG is to calculate the gra-

dient of our cost function C . In order to facilitate this

phase, we have changed the equation (4) by :

C (f, Θ) =

∑

i=1

∑

j=1

(C r(f, θ

, j))

(7)

with C r(f, θ

, j) = π

−

∑

k=1

, j

Now we calculate the ∇C r then we will deduct the

∇C . Due to the discrete nature of the cost function,

we use the ﬁnite difference to estimate the gradient

values.

For h = 1, . . . , N, the f

-th partial derivative of C

is given by

∂C r

∂f

= −w

, j

which leads to,

∂(C r)

∂f

= −2w

, j

−

∑

k=1

, j

Then,

∂C

∂f

= −

∑

i=1

∑

j=1

, j

−

∑

k=1

, j

In the same, we have for the h-th derivative ac-

cording to Θ, ∀h = 1, . . . , M.

∂C r

∂θ

2∆

∑

k=1

(θ

−∆

), j

− w

(θ

+∆

), j

where w

(θ

+∆

), j

, w

(θ

−∆

), j

are the projection coefﬁ-

cients according to θ

+ ∆

, θ

− ∆

, ∆

here is the ﬁ-

nite difference used in the gradient calculation. which

leads to,

∂(C r)

∂θ

∆

∑

k=1

(θ

−∆

), j

− w

(θ

+∆

), j

−

∑

k=1

, j

Then,

∂C

∂θ

2∆

∑

j=1

∑

k=1

(θ

−∆

), j

− w

(θ

+∆

), j

−

∑

k=1

, j

We noticed that according a small value to the pa-

rameter ∆

may produce a null derivative for some

angles because of the discrete nature of the rotation

which may boil down to the identity map for the small

angle changes. Therefore, after many experiments we

found that the most suitable value is 1

◦

After computing the gradient, we can proceed to

the optimization phase. Firstly, we reconstruct the ini-

tial object; in our case, we chose to use the algebraic

reconstruction method SIRT for this phase. However,

any algorithm either analytic or algebraic is can be

used. Secondly, we take the initial reconstructed ob-

ject and the projection data with the tilt angles used in

the acquisition as input for the iterative CG algorithm.

The algorithm of our approach is showed in Alg.1.

Algorithm 1: CG reﬁnement algorithm.

initialization f

= f

init

, Θ

= Θ

init

, cond=0

while iter < iter

max

AND cond=0 do

compute gradient ∇C (f

iter

, Θ

iter

)

compute f

iter+1

, Θ

iter+1

with the CG

∆C = C (f

iter

, Θ

iter

) − C (f

iter+1

, Θ

iter+1

)

if ∆C < ε then

cond=1

end if

iter

← f

iter+1

, Θ

iter

← Θ

iter+1

, iter ← iter+ 1

end while

return f

iter+1

, Θ

iter+1

5 RESULTS

Several experiments were conducted to assess the ef-

ﬁciency of the proposed method on 2D and 3D data.

The tilt angles used for 2D tests are between −70

◦

and 70

◦

with a 2

◦

tilt step. For each angle a random

error in [−1.5

◦

1.5

◦

] is added. For the 3D tests, We

used a different set of angles, one similar to the set

used in cryo-ET. The boundaries are the same, but the

tilt step is different. The step used between −50

◦

and

◦

is 5

◦

and it is 2

◦

for the others. One can notes that

the number of tilt angles for the 3D case is less than

the 2D, which makes the reﬁnement harder. Along

the projection noise, we used three sets of tilt angles:

the real one, one with absolute value of the random

error ≤ 1

◦

and one with random error ≤ 2

◦

Angular Uncertainty Reﬁnement and Image Reconstruction Improvement in Cryo-electron Tomography

To measure the quality of reconstruction, we pro-

pose two evaluation criteria. The ﬁrst is the cross-

correlation coefﬁcient (equation (8)). It is a criterion

to measure the degree of similarity between the orig-

inal image and the reconstructed image. This coef-

ﬁcient is equal to 1 when the reconstructed image

coincides exactly with the original image and zero

otherwise. The second criterion is Normalized Root

Mean Square Error (NRMSE) deﬁned by the equa-

tion (9). Unlike the correlation coefﬁcient, the zero of

the NRMSE means a better result. We use NRMSE to

measure the quality of angles correction produced by

our approach. The equation (10) shows the Measure

of Angle Correction (MAC). More the MAC value is

close to zero, the more the angles found by our ap-

proach are corrects.

Corr =

∑

k=1

− M(f))(

− M(

f))

∑

k=1

− M(f))

∑

k=1

(

− M(

f))

(8)

NRMSE =

∑

i=1

(θ

−

)

max(Θ) − min(Θ)

(9)

MAC = 1 −

NRMSE

init

− NRMSE

final

NRMSE

init

(10)

With NRMSE

init

and NRMSE

final

are respectively

the NRMSE between the true angles, the angles be-

fore the optimization and the angles after the opti-

mization. Thus, if the angles after the optimization

are totally corrected NRMSE

final

will be zero, which

means the MAC will be zero also. However, if the er-

rors are not corrected or even are ampliﬁed, the MAC

will be greater than 1.

The 2D experiments involve 122 2D synthetic

gray-level images randomly generated at different

resolutions N×N with N = 32, 64, 128, 256, 512. A

sample of the synthetic images used are shown in the

ﬁgure 3. The same number of iterations are applied

on all the experiments images.

Figure 3: 2D synthetic images.

All the projections were corrupted with different

levels of Gaussian noise σ and a random error has

been assigned to each of the tilt angles (some samples

are shown in Fig. 5).

The mean results of the synthetic data are gathered

in Tab. 1 and the tilt angles reﬁnements of one of the

tests are presented in Fig. 4.

Figure 4: Error enhancement between the original tilt an-

gles and the corrected ones for one of the test images.

For all the tested resolutions, the error that re-

mains after optimization is under 30% of wrong pix-

els and under 20% of wrong projection angles. In our

future work, we will investigate deeper the relation

between the image size and the number of iterations

to reach the minimum. We notice also that more the

gray-levels we use, more the discrete research space

is connected and more the method is robust to noise.

Table 1: Evaluation of 2D synthetic data.

Noise variance σ 0 2 4 6 8

Corr 0.97 0.93 0.88 0.87 0.83

MAC 0.09 0.12 0.15 0.18 0.19

Sinogram SIRT Our method

σ = 0σ = 4σ = 8

Figure 5: The sinogram of a single image is corrupted with

Gaussian noise of different variances σ. The reconstruction

by SIRT (Penczek, 2010) and our method is shown for each

noise level.

The 3D experiments were done on synthetic

and real data. A set of 3D synthetic gray-level

volumes were created with different resolutions

(N = 16, 32, 64, 128). Fig. 7 shows a 3D volume

with its results. The real data are projections of the

Orf-parapoxvirus: Fig. 6: presents some of those pro-

jections.

Figure 6: Orf-parapoxvirus projections respectively accord-

ing to the angles -60

◦

, -40

◦

, -10

◦

, 20

◦

, and 50

◦

The mean results according to deferent angular er-

ror (AE) and noise variance σ sing the same evalua-

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

100

Figure 7: Reconstruction of a synthetic 3D; left: 3D volume

(N = 32), center: with our method and right: with SIRT.

tion measures used for the 2D evaluation are given in

the Tab. 2 and Tab. 3.

In this two table, one can notice the promising re-

sults, the correlation is very high over all the testing

seniors. The same for the MAC results that are low

for the most of the testing seniors. We notice also,

that when we use the true angles, they are slightly cor-

rupted by our algorithm.

Table 2: Corr results for 3D synthetic data.

◦

≤ 1

◦

≤ 2

◦

0.5 0.97 0.89 0.88

2 0.90 0.84 0.85

5 0.88 0.77 0.75

Table 3: MAC results for 3D synthetic data.

◦

≤ 1

◦

≤ 2

◦

0.5 0.01 0.09 0.08

2 0.05 0.13 0.14

5 0.07 0.18 0.21

For the Orf-parapoxvirus reconstruction, we cal-

culate the improvement rate of resolution, which was

21.86%, which we think it is a good result consider-

ing that we used volume and angular reﬁnement only.

Also, we sought an opinion of an expert in the biol-

ogy ﬁeld and he validate the amelioration of the re-

construction object generated by our approach. Some

of the 2D slice of the reconstructed object by our ap-

proach and SIRT are presented in Tab. 4.

Table 4: Some of the 2D slices of the reconstructed object

by SIRT and our approach.

SIRT

Our approach

6 CONCLUSION

In this paper, we have described a method to reﬁne

the reconstruction of an object from a set of its to-

mographic projections and simultaneously correct the

errors over the used tilt angles. The starting point of

the proposed method is an approximation of the ob-

ject (provided by some reconstruction algorithm) to-

gether with a set of uncertain tilt angles used to ac-

quire the projections. Then, considering both the an-

gles and the values of the reconstructed volume as

parameters, we minimize the Euclidean distance be-

tween our ground truth (the original tomographic pro-

jections) and the re-projections of the estimated object

according to the current corrected set of angles. For

the optimization process, a non-linear conjugate gra-

dient algorithm is used. Our experiments shows that

the proposed method improves the reconstruction of

the object compared to using SIRT directly. Further

improvements of the reconstruction can still be ob-

tained in the frame of our method. In our future work,

we plan also to incorporate the other transform pa-

rameters of the alignment process, also, the correction

of the contrast transfer function in the optimization

process.

REFERENCES

Brandt, S. and Ziese, U. (2006). Automatic TEM im-

age alignment by trifocal geometry. Journal of Mi-

croscopy, 222:1–14.

Colliex, C. (1998). The Electron Microscopy. Presses Uni-

versitaires de France.

Dai, Y. H. and Yuan, Y. (1999). A nonlinear conjugate gra-

dient method with a strong global convergence prop-

erty. SIAM J. on Optimization, 10(1):177–182.

Egerton, R., Li, P., and Malac, M. (2004). Radiation dam-

age in the TEM and SEM. Micron, 35(6):399–409.

Frank, J. (2006). Electron tomography: methods for three-

dimensional visualization of structures in the cell.

Springer.

Gilbert, P. (1972). Iterative methods for the three-

dimensional reconstruction of an object from projec-

tions. Journal of Theoretical Biology, 36(1):105–117.

Gordon, R., Bender, R., and Herman, G. (1970). Al-

gebraic Reconstruction Techniques (ART) for three-

dimensional electron microscopy and X-ray photog-

raphy. J Theor Biol, 29(3):471–481.

Joseph, P. (1982). An improved algorithm for reprojecting

rays through pixel images. Medical Imaging, IEEE

Transactions on, 1(3):192–196.

Man, B. D. and Basu, S. (2004). Distance-driven projection

and backprojection in three dimensions. Physics in

Medicine and Biology, 49(11):2463.

Angular Uncertainty Reﬁnement and Image Reconstruction Improvement in Cryo-electron Tomography

101

Nocedal, J. and Wright, S. (2006). Numerical Optimization.

Springer Series in Operations Research and Financial

Engineering. Springer-Verlag New York, 2 edition.

Penczek, P. (2010). Chapter one - fundamentals of

three-dimensional reconstruction from projections. In

Grant, J., editor, Cryo-EM, Part B: 3-D Reconstruc-

tion, volume 482 of Methods in Enzymology, pages

1–33. Academic Press.

Sorzano, C., Messaoudi, C., Eibauer, M., Bilbao-Castro,

J., Hegerl, R., Nickell, S., Marco, S., and Carazo, J.

(2009). Marker-free image registration of electron to-

mography tilt-series. BMC Bioinformatics, 10(1):124.

Stagg, S., Lander, G., Pulokas, J., Fellmann, D., Cheng, A.,

Quispe, J., Mallick, S., Avila, R., Carragher, B., and

C.S.Potter (2006). Automated cryo-em data acquisi-

tion and analysis of 284742 particles of groel. J Struct

Biol, 155:470–481.

Tran, V.-D., Moreaud, M., Thi´ebaut, E., Denis, L., and

Becker, J. M. (2013). Inverse Problem Approach for

the Alignment of Electron Tomographic Series. Oil &

Gas Science and Technology - Revue d’IFP Energies

nouvelles, 69(2):279–291.

Yang, C., Ng, E., and Penczek, P. (2005). Uniﬁed 3-D struc-

ture and projection orientation reﬁnement using quasi-

Newton algorithm. J Struct Biol, 149(1):53–64.

Zheng, Q., Sedat, J., and Agard, D. (2010). Automated

data collection for electron microscopic tomography.

Methods in Enzymology, 481(10):283–315.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

102