
Improved Model of Social Networks Dynamics
Jiří Jelínek and
Roman Klimeš
University of South Bohemia in Ceske Budejovice, Faculty of Science, Branisovska 1760,
370 05, Ceske Budejovice, Czech Republic
Keywords: Social Networks, Dissemination of Knowledge and Information, Modeling, Simulation.
Abstract: Social networks are currently the most studied structures due to their popularity among IT users. In our paper
we will focus on the dynamics of the dissemination of information in these networks. We will introduce the
advanced heuristic conceptual model of individuals’ behavior in the network which is based on need for
information and knowledge for solving specific problems; the proposed multi-agent model of the social
networks dynamics is based on this concept. This version of the model was adapted for scale-free and growing
networks. Experiments conducted with new model were focused on verifying its behavior with respect to
knowledge about the type of modeled networks and on observation of dynamic effects in them; the results
will be presented as well.
1 INTRODUCTION
Social networks are currently the most studied
structures in the area of exchange of information and
knowledge and their static behavior is often studied,
slightly less their dynamics.
Social network means any group of
interconnected people in which persons are linked by
links. These links may represent a relationship, job,
or even a common hobby. It is therefore an oriented
graph of interconnected nodes (or agents, if we use
multiagent modelling), where nodes represent
individuals and edges of the graph the links between
them. The dynamics of the network is then
represented by changes of nodes and links, both in
their number and behavior or placement in time.
Social networks themselves are not the product of
IT, but these technologies support them more or less.
As a result of high level IT support we can talk about
online social networks (Arnaboldi, 2013) that have
signs of complex growing networks with typical
behavior.
In our previous work we proposed the model of
information dissemination dynamics in social
networks based on closed world assumption with high
preferences of communication between agents
(described below). The model described in this paper
aims to improve the previous one especially in more
real agent’s behavior and in the suitability for
complex and growing networks described with scale-
free models. We also want to introduce experimental
results demonstrating the effect of the improvements
as well as some phenomena which can be observed in
the dynamics of modeled networks.
The model can be used for investigating the
dynamics in complex scale-free networks created or
used for the transmission and dissemination of
information and knowledge (e.g. corporate networks,
online services, etc.), its use is therefore not limited
to online networks and purely electronic transfer of
information.
2 RELATED WORK
As mentioned above, social networks are often
researched structures. Their theoretical models can be
divided into three basic groups - models of random
graph, small world models and models whose
structure is independent on the size of the network,
i.e. scale-free models. Detailed descriptions of all
three groups can be found in (Newman, 2006). More
information about the investigation of static graphs
and their properties using traditional social network
analysis and its methods can also be found in (Klimeš,
2012).
Jelínek, J. and Klimeš, R.
Improved Model of Social Networks Dynamics.
DOI: 10.5220/0005682701410148
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 1, pages 141-148
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
141

2.1 Common Features of Complex
Networks
As complex ones we consider the social networks
with complex topology, whose behavior may vary
over time. Aforementioned scale-free models are best
suited for a description of these networks.
The notion of scale-free networks was introduced
by Barabási and Albert in 1999 (Barabási, 1999).
These networks have common features regardless of
the size and complexity and can be used to describe
so different systems such as the World Wide Web or
citation or metabolic networks. The structure of these
networks is therefore likely to be formed by the same
principle.
The mechanism, that Barabási and Albert proposed
to describe the scale-free networks, had two basic
assumptions. First, network grows and new nodes are
added to it gradually. This assumption is certainly met
for social networks, but was not respected in the
models based on the principles of random graph or
small world, where the network is considered static in
terms of number of nodes. Second, the nodes acquire
new links proportionally to the number of links that
already have. Authors called this process preferential
attachment.
Barabási and Albert suggested model (Barabási,
1999), in which network grows each time step by
adding one node connected with m links to the nodes
selected randomly with a probability proportional to
their degree. Only the results of this process are
monitored, but not its dynamics. The described state
may not occur immediately after adding a new agent,
but may be the result of gradual modification of the
network structure made in accordance with the
objectives of the individual.
Preferential attachment is formally defined by
formula (1). Let k
i
be the degree (number of
connections) of node i. Then, the probability that the
newcomer node connects to node i is defined as the
ratio of the degree of node i and the sum of the
degrees of all nodes in the network.
Π
(
)
=
∑
(1)
As already mentioned, the above mechanism
describes results of the process, our aim was to
examine its dynamics as well.
2.2 Properties of Complex Networks
Examining complex networks, some interesting
information about their structure was discovered. It
should be emphasized that most of these findings
focus on the static description of the network. The
first one concerns the degree of each node.
The considerations about the distribution of
degree values in a network can be found very often
(Arnaboldi, 2013; Kas, 2013). Formally we talk about
the probability distribution P(k) that
a randomly selected node has a degree k.
One wonders whether there is a typical probability
distribution of degree values in the network. It can be
found in the models of random graphs, usually an
equivalent to Poisson distribution. The degree
distribution in real complex networks can be usually
described by power law (Newman, 2006) defined by
formula (2).
(
)
~
(2)
Therefore, in complex networks there are several
nodes with significantly high degree (widely
connected) and the degrees of other nodes are falling
very quickly (poorly interconnected). So it is
a network with a small number of key individuals,
who are connected to most other individuals in the
network. The hyperbolic shape of the distribution
depends on the parameter γ > 1, and usually ranges in
[2, 3] (Newman, 2006). We agree with this principle,
if we don’t take into account personal characteristics
of individuals in the network, which could
significantly affect linking agents and can weaken the
power law application.
Clustering is also the endpoint of social
networking. We can find it in many studies dealing
with social networks (Arnaboldi, 2013; Kas, 2013;
Zhao, 2012; Allodi, 2011). Clustering coefficient
indicates whether or how much the neighbors of a
node are interconnected or simply whether the
individual's neighbors in the network (e.g. friends)
communicate and know each other. Clustering
coefficient is defined by formula (3).
=
(
−1)
(3)
Variable k
v
represents the degree of
a node v and e
v
the number of interconnected pairs of
these neighbors. This formula assumes the oriented
links in the network. Clustering coefficient takes
values in the interval [0, 1], where the value
0 indicates that even one pair of neighbors is not
connected and the value 1 that all neighbor pairs are
interconnected.
2.3 The Original Model
Our work is based on the agent based model described
in (Jelínek, 2011) and further expands and improves
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
142

it. The mentioned model assumes the coexistence and
interaction of individual agents representing persons
and is focused on a detailed examination of their
behavior in the process of acquiring the necessary
knowledge.
The agents “exist” in the given area and they are
exposed to "life" situations requiring their reaction
(solution of the situation). Each situation can be
considered as message of type s that agent randomly
(with given probability in each simulation step) and
repeatedly receives and needs to find the best
response r to it, which can be described as r = f(s).
We assume, that we are able to describe the quality q
r
of reaction as a function q
r
= g(r) with values in the
interval [0, 1]; the value 1 corresponds to best
response. As an example we can present the situation
requiring the writing of the test (message of type s).
The agent reacts to it by answering the test questions
r = f(s) in quality q
r
from [0, 1].
The function f is specific for each agent in
network and is based on: (i) agent’s quality (quality
of his knowledge) and (ii) the information stored in
agent’s memory and also (iii) on reactions on the
same message type adopted in the past by other agents
that communicate with the current one (partners). In
our example the agent can generate the answer to test
questions from his knowledge or can take the
information from memory or tries to find answers
through communication with partners (e.g. friends).
In the process of finding the best reaction to the
given situation plays a crucial role the g function
which defines what is “the best”. This function is
same over the network for every message type. The
model respects the fact that the reaction may not be
evaluated immediately after its adoption, but after
some period of time. The information about
evaluation is represented by a special message sent to
the agent. In our example the agent immediately
doesn’t know how good his answers to test questions
were, but after checking by the evaluator.
Agent stores every used reaction in memory
together with identification of its author. The author
necessarily doesn´t need to be the agent from whom
the reaction was obtained; it could be taken over from
another individual in the network. There is
implemented the forgetting process in the memory –
old, not used and not very good reactions are
continuously removed from memory.
Every agent rates other agents in network that are
in his partner list for his purposes. Authors of the used
reactions are added to this list of partners and their
ratings are updated in the moment of evaluation of
reaction proposed by them. Rating is then used in
situations where any evaluated message reaction is
neither available in the agent’s memory nor obtained
from the network. The rating is decreased when the
partner does not want to communicate and answer
agent’s questions. The length of the partner list
(number of links) is limited and agents with lowest
ratings are deleted.
The model uses a closed world assumption
applied on the number of agents in the network as
well as the size of the set of possible situation types
that both are constant and unchanging over time.
A detailed description of the model can be found in
(Jelínek, 2011).
We can say that this model well describes the
social networks, whose primary purpose is the
distribution and sharing of knowledge (relevant
reactions to messages), as well as the internal
principles in these networks. But experiments show
that closed world assumption is not suitable for
complex and growing networks and that behavioral
algorithms used are not ideally set up and distort the
model behavior in comparison to the one observed on
real networks. The problems were in mechanism of
best reaction selection (preference of communication
with partners before generating own reaction or using
information from agent’s memory) and in partner list
management (storing only authors of used solutions).
Therefore the model was revised and the results of
this process are described in the following chapter.
3 MODEL MODIFICATIONS
As already mentioned, the original model of
knowledge-based social network provides useful
outputs for exploring the dynamics of certain social
network types. This model was further developed in
two directions. First, we made improvements in
internal mechanisms of agent behavior, especially in
communication with other network partners. Second,
there was the restructuring of the model to eliminate
the closed world assumption. The aim of the changes
was to prepare the model for using in scale-free and
growing social networks.
3.1 The Internal Mechanisms
According to experiments with the original model the
internal behavior of the agent was modified in the
phase of finding the best possible response to the
input situation. The old model favored using
knowledge from the social network, but the use of
agent’s parameter which characterizes the
willingness or ability of the agent to establish
communication links with partners is more accurate.
Improved Model of Social Networks Dynamics
143
This parameter takes values from [0, 1] and is
understood to be the probability that an agent will try
to get reactions via communication with the network
partners. If this does not occur, the agent will use his
own generated reaction to a given situation or will use
memory data (previously stored reactions). This
approach respects more the reality of life and the
diversity of agents’ personalities through the used
stochastic element.
The second modification was adding the method
for continuous update of agent’s acceptance
parameter describing the agent's willingness to
respond to other agents’ questions on the best reaction
to certain type of message. This can be understood as
maximum probability which agent answers the
question with. We talk about maximum value because
it is common in the real world that the willingness to
answer will decrease for individuals extremely
overloaded by questions. This phenomenon has been
implemented into the model through continuous (in
each simulation step) parameter updates according to
formula (4).
=
,
1+
−
(4)
Variable a
act
represents the acceptance parameter in
current simulation step, k
a
the coefficient of influence
of deviation from the ideal expected number of
questions in one step n
opt
and n the real number of
questions in the step. The symbol a
orig
indicates the
acceptance value set at the beginning of the
simulation as a personal characteristic of the agent.
The a
new
for the next simulation step is thus moved in
the interval [0, a
orig
].
Next model modification also concerns the agent
communication. If the partner was asked but he did
not answer, his rating in modified model is decreased.
The consequence of this is gradually shifting of the
partner to the bottom of the partner list and in the case
of exceeding of the maximum length removing the
partner from list. This corresponds to real behavior of
individuals – I will not communicate with persons not
responding to my questions.
The last change was made in agents’ partner lists.
The agent asking question that has been answered by
queried agent is now also added to the queried agent
partner list with a minimum rating. This well
simulates the fact, that when we are asked, we are
generally aware of who asked us and we are able to
contact him in future communications.
3.2 Closed World Limit Elimination
Closed world assumption was one of the basic and
most limited features of the original model. The
proposed modification eliminates this assumption,
both in terms of the number of message types and in
the number of agents in the network.
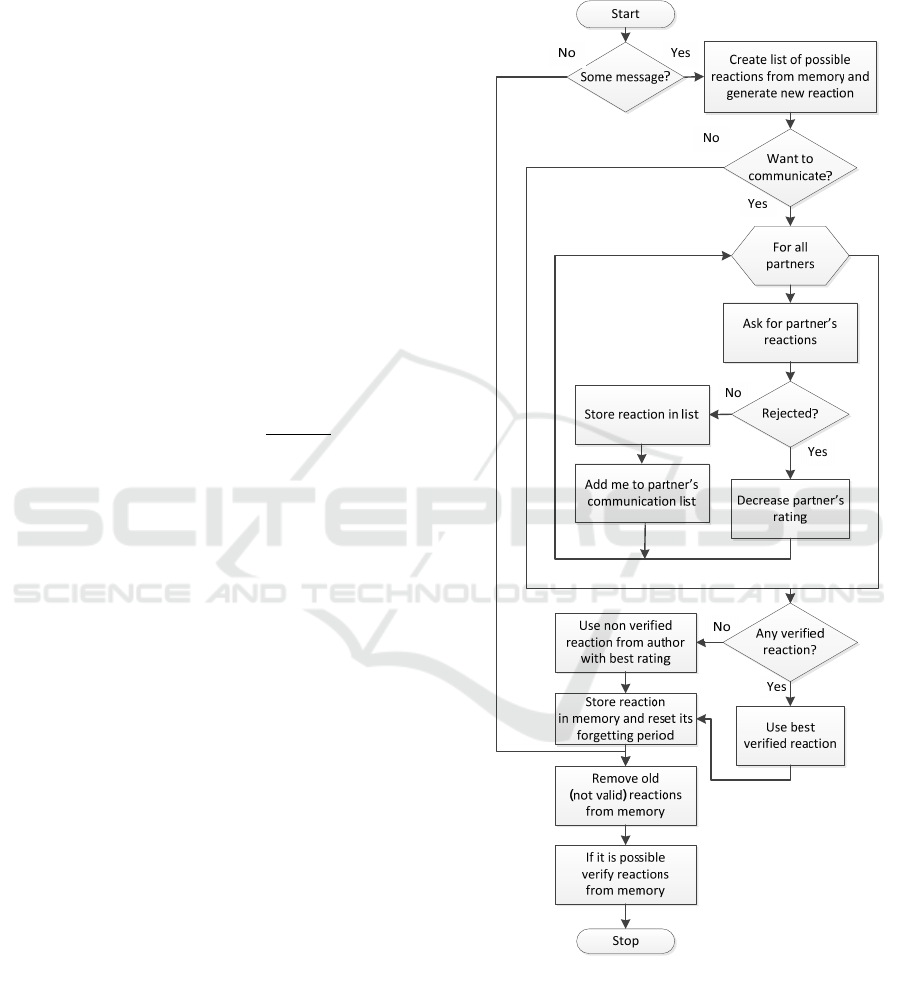
Figure 1: Algorithm for one simulation step of one agent.
The introduction of a flexible number of
situations, the agent must respond, was caused by
efforts to model a reality accurately - we are also
exposed to stimuli or situations that are completely
new for us and we try to deal with them. New
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
144
situations can thus be injected into the model also in
the course of the simulation process.
However, to get closer to reality, it was necessary
to make a substantive change in the agent generation
of new reactions. In original model this process
assumed the setting of one parameter of the agent
which basically expresses agent's level of intelligence
and knowledge and thus the ability to generate good
reactions. But if we start from the assumption, that
different message types need knowledge from
different (knowledge) domain, it is very likely that the
individual will not be able to react to all of these
messages with the same quality level. Therefore the
level of agent’s knowledge is now set separately for
each message type.
The last modification was made to enable network
expansion by adding new agents into it. Usually, in
the scale-free social networks, we assume that
individuals do not leave these networks, but a large
number of new people are coming into them. This
corresponds to large online networks.
Now it is possible to insert a new individual into
modified model at any time of the simulation and
initialize the list of his partners to the m nearest
neighbors in the 2D visualization space (which may
not be necessarily the real geographical one). This
fact is based on the assumption that the agent
embedded in the environment of social networks will
try to establish links and relationships with relatives
or acquaintances first. These starting links will be
subsequently changed during simulation to respect
agent's aim and made the social network the most
beneficial for him. It means he will be able to obtain
reactions of good quality for different message types
(see preferential attachment mentioned above). The
variable m was added to the model as a new adjustable
parameter.
The final algorithm of searching reaction
implemented in the model is shown in Fig. 1.
4 EXPERIMENTS
This chapter presents the results of experiments
realized with the modified model described in chapter
3. The purpose of all experiments was to verify the
behavior of the new model and effect of realized
modifications. All experiments were performed with
1000 simulation steps. The maximum number of
agent’s partners was set to 20 and the number of
initial links for new agents was set to m = 5. Growing
network (mentioned in this chapter) is the network
with only one agent at the beginning growing by one
agent in each step of simulation.
4.1 Degree Distribution
The probability distribution of network nodes degrees
was examined in the first experiment. The links
between the agents in the model are oriented, so we
can talk about two degrees - edges entering the node
(indegree - d
i
) and the degree defined by links
outgoing from the node (outdegree - d
o
). Every agent
keeps a list of his partners, which can be used to find
a reaction in the case of exposure to the message. The
size of the list is defined by d
o
. Degree d
i
represents
the number of agents having given agent as a partner
in their lists.
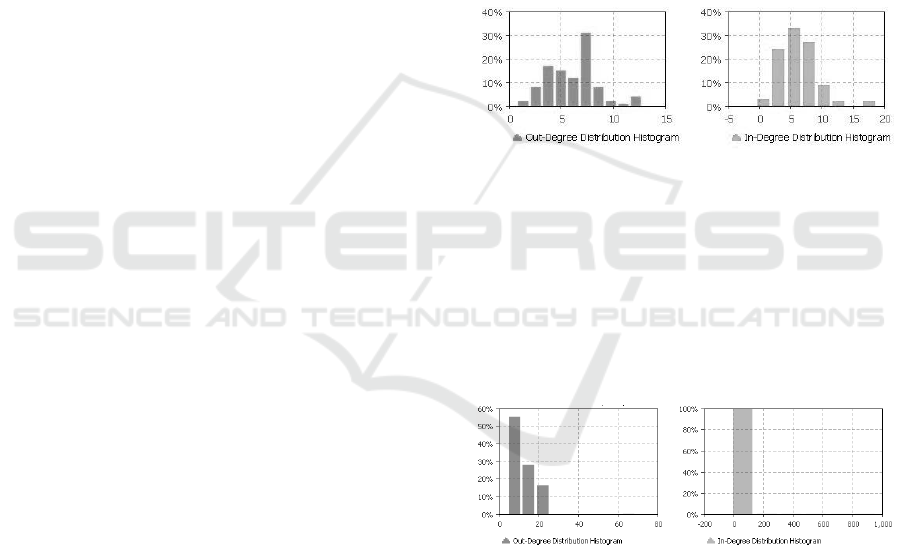
Fig. 2 shows a histogram of the degree
distribution on a static network of 100 agents exposed
to only one situation in the original model.
Figure 2: Degree distributions of static network.
The shape of histograms approximates to the Poisson
or Gauss distribution, which corresponds to random
graphs. From chapter 2.1, however, we know that
large-scale social networks are scale-free and their
degree distribution should be totally different. Fig. 3
shows the degree distribution in the growing network
whose parameters were identical to the previous one,
but the modified model was used.
Figure 3: Degree distributions of growing network.
We can see that the degree distribution has
fundamentally changed and can be reasonably well
approximated by the above-described power law.
Therefore, the model behavior is now closer to real
social networks.
4.2 Preferential Attachment
As already mentioned in chapter 2, through the
research of real social networks the mechanism of
preferential attachment was discovered. The modified
Improved Model of Social Networks Dynamics
145

model allows studying the dynamics of this
mechanism.
After entering the network the agent is connected
to the m nearest neighbors. Thus the effect of
preferential attachment is not shown immediately, but
in the dynamics of the link development which agent
adjusts to achieve maximum profit from membership
in the network. Fig. 4 shows a graph of the time
evolution of the metrics d
norm
defined by formula (5).
=
1
1
(5)
N represents the total number of agents in the network,
P
k
is the size of the partner list of the agent k, d
ij
is
indegree of partner j from the list of partners P
k
. The
d
norm
then shows the average quality (or value) of each
link in the network, respectively the quality of partner
which this link points to. In case of application of
preferential attachment rule this value will be
increasing in the time, which was tested on the above
defined growing network with the result in Fig. 4.
Figure 4: Average quality of outgoing links.
The chart shows that agents were continually
increasing the quality of their outgoing links during
the simulation – the links were redirected to partners
with the highest indegree level. The confirmation of
preferential attachment can be seen in this process,
which is described only in its final state in chapter 2.
The graph shows the ripples of observed value that
were not caused by the changes in model settings.
These could be interpreted as findings of significant
(high indegree) individuals in the network, which are
then used by many other agents to target their links.
4.3 Clustering Coefficient
In a similar manner we investigated also a clustering
coefficient which was affected by model
modifications. Fig. 5 shows the average network
clustering coefficient evolution in time for the
growing network.
Figure 5: Average clustering coefficient in time.
We can see in the graph that the average value was
falling steadily, with ripples corresponding to Fig. 4.
It is obvious that the existing capacity of outgoing
links (limited size of the partner list) is redirected out
of interconnected clusters with the increasing focus
on the best partners (because they do not bring new
knowledge) towards higher quality resources that are
shared with agents unconnected to each other.
We should mention that clustering was measured
on the basis of outgoing links of agents.
4.4 Acceptance Modification
The modification of agents’ behavior in the state of
a large number of incoming questions brought
significant changes in the structure of the network.
Network structure created with the original model can
be seen in Fig. 6.The structure of the network in this
case corresponds to the network with significant
individuals with considerable capacity to respond to
questions (node size corresponds to its popularity in
the network calculated as the sum of ratings of the
agent across all agents in the network – agent not
presented in partner list has rating = 0). The network
also illustrates the preferential attachment very well,
but does not reflect a state when the agent may be
overloaded with incoming questions.
The structure of modeled network has changed
dramatically after modifying the model behavior
reflecting declining willingness to answer questions
in the case of their large number. This better
corresponds with real individuals’ behavior. For this
experiment the ideal number of questions in every
simulation step was set to n
opt
= 1. Results are shown
in Fig. 7.
The effect of overloading on the network structure
is obvious - implemented mechanism does not allow
extreme load of individuals by questions and as a
result also their extreme popularity (rating downgrade
used for agents not answering questions).
Functionality of this mechanism is also shown in the
2D histogram of acceptance values on agent’s
popularity in the state when agents largely acquire
solutions through communication and when
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
146
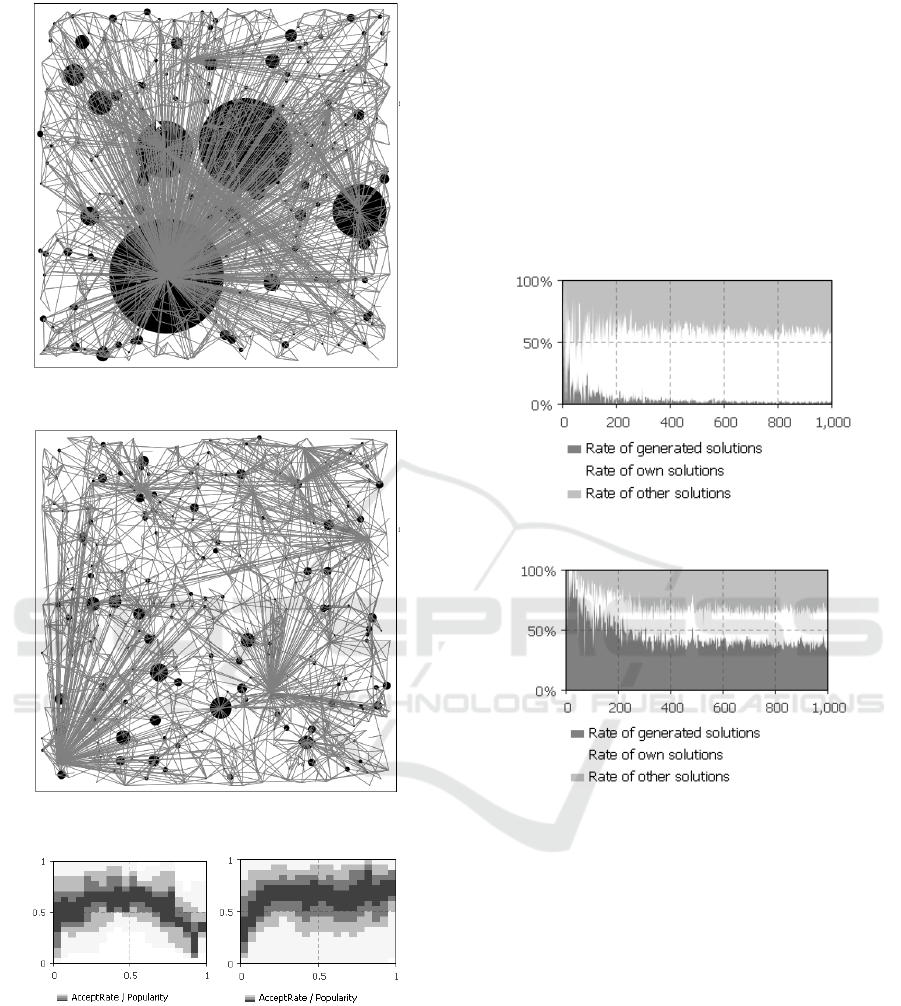
Figure 6: Structure of the network in original model.
Figure 7: Structure of the network in modified model.
Figure 8: 2D Histogram of acceptance on agent popularity.
acceptance value of popular agents is reduced (Fig. 8
left), and in the steady state, when the solutions are
mostly recalled from agent’s own memory and
communication is not so intensive and is not
necessary to regulate it (Fig. 8 right).
4.5 Flexible Number of Message Types
The following experiment was aimed to examine the
impact of model modifications focused on working
with more types of messages, other settings remained
unchanged. Fig. 9 and 10 show the comparison of
ratio of generated solutions, the ones recalled from
the memory and also obtained through the
communication. There is the network with just
1 message type in Fig. 9. Fig. 10 shows the results in
network with 20 message types (time on x-axis).
Figure 9: Ratio of reaction sources for 1 message type.
Figure 10: Ratio of reaction sources for 20 message types.
The chart shows that a larger number of message
types caused a greater need to generate own reactions
especially at the beginning. Adaptation of the
network on more complex task (20 message types)
took longer time. The number of generated reactions
was still higher than in case of one message type even
in a steady state. This corresponds to reality - in the
case of a variety of stimuli, the optimization of list of
partners lasts longer and the overall quality of the
solutions is lower (agents do not generate the same
high quality solutions for all message types, the
number of links is limited).
Improved Model of Social Networks Dynamics
147

5 CONCLUSIONS
In this paper we described the modified model for
simulating the dynamics of the exchange of
information and knowledge within a social network.
Two groups of modifications were implemented on
the original model with the aim to move the behavior
of the model closer to reality of real scale-free and
growing social networks. The first group of changes
was focused on internal agent processes, especially
on communication processes and agent rating
modification. The second group was targeted on
elimination of restrictions connected with the closed-
world assumption.
There were subsequently conducted experiments
with the modified model to verify the effect of the
changes on the behavior of the model and also
experiments investigating the behavior of the model
from the point of view of the known properties of
complex social networks.
Better simulation of power law for degree
distribution that can be found in real networks was
experimentally proven. Experimental results also
show the influence of agents’ quality on clustering
coefficient.
The model was also modified in the simulation of
decision made by agents, where the behavior was
adapted to respect the agent’s communication
preferences; the emphasis on agent’s own intelligence
was also increased.
The mechanism for modeling the growing
networks was implemented and the dynamics of
preferential attachment rule was shown. The
mechanism of agent’s rating could be further
modified towards diversification of partners’ rating
according to the message type.
As a conclusion we can say that the generated
simulation model now better simulates scale-free real
social networks aimed at disseminating knowledge
through implementing several known principles of
these networks.
The model is still constantly being expanded,
modified and investigated. Subsequent work will
focus on further improving the internal mechanisms
of agents’ behavior and exploring the impact of input
parameters on model outputs. Finally we will also try
to validate the model using the data from real-world
social networks.
REFERENCES
Allodi, L., Chiodi, L., & Cremonini, M. (2011, December).
The asymmetric diffusion of trust between
communities: simulations in dynamic social networks.
In Proceedings of the Winter Simulation
Conference (pp. 3146-3157). Winter Simulation
Conference.
Arnaboldi, V., Conti, M., Passarella, A., & Dunbar, R.
(2013, October). Dynamics of personal social
relationships in online social networks: A study on
twitter. In Proceedings of the first ACM conference on
Online social networks(pp. 15-26). ACM.
Barabási, A. L., Albert, R., & Jeong, H. (1999). Mean-field
theory for scale-free random networks. Physica A:
Statistical Mechanics and its Applications,272(1), 173-
187.
Jelínek, J. (2011). Modelování informačních toků v
sociálních sítích. Znalosti 2011 - Czech and Slovak
Knowledge Technology Konference, Stará Lesná, SR,
31. 1. 2011 - 2. 2. 2011. In CEUR Workshop
Proceedings, Vol-802, http://ceur-ws.org/Vol-802/
(online).
Kas, M., Carley, K. M., & Carley, L. R. (2013, August).
Incremental closeness centrality for dynamically
changing social networks. In Advances in Social
Networks Analysis and Mining (ASONAM), 2013
IEEE/ACM International Conference (pp. 1250-1258).
IEEE.
Klimeš, R. (2012). Využití sociálních sítí v organizaci. [The
Use of Social Network in Organization. Bc. Thesis, in
Czech.] – 49 p., Faculty of Science, University of South
Bohemia, České Budějovice, Czech Republic.
Newman, M., Barabasi, A. L., & Watts, D. J. (2006). The
structure and dynamics of networks. Princeton
University Press.
Zhao, X., Sala, A., Wilson, C., Wang, X., Gaito, S., Zheng,
H., & Zhao, B. Y. (2012, November). Multi-scale
dynamics in a massive online social network. In
Proceedings of the 2012 ACM conference on Internet
measurement konference (pp. 171-184). ACM.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
148
