Optimizing Energy Absorption for Ultrashort Pulse Laser Ablation of

Fused Silica

Nicolas Sanner, Maxime Lebugle, Nadezda Varkentina, Marc Sentis and Olivier Utéza

Aix-Marseille Univ., CNRS, LP3 UMR 7341, 163 avenue de Luminy C.917, 13288 Marseille, France

Keywords: Ultrashort Laser-matter Interaction, Dielectric Materials, Ablation.

Abstract: We investigate the ultrafast absorption of fused silica irradiated by a single 500 fs laser pulse in the context

of micromachining applications. As the absorption of the laser energy is rapid (~fs), the optical properties of

the material evolve during the laser pulse, thereby yielding a feedback on the dynamics of absorption and

consequently on the amount of energy that is absorbed. Through complete investigation of energy

absorption, by combining “pump depletion” and “pump-probe” experiments in a wide range of incident

fluences above the ablation threshold, we demonstrate the existence of an optimal fluence range, enabling to

turn transiently the material into a state such that each photon is optimally utilized for ablation.

1 INTRODUCTION

Ultrashort laser pulses are extremely interesting and

powerful tools for laser-matter interaction. The

spatial accuracy of energy deposition into matter

combined with the shortness of the energy

deposition step enable to reach relatively high

intensities (10

-10

W.cm

-2

) while using low

energies, capable to push matter into strongly non-

equilibrium conditions (Gamaly, 2011). The fast

creation of highly excited plasmas at solid densities

provides notably cutting-edge capabilities for

controlled modification of matter. Near-IR

wavelengths of most current femtosecond laser

sources are particularly well adapted to trigger

highly-nonlinear absorption in transparent dielectric

materials (silica, sapphire, diamond…), whose range

of applications for material science and photonics is

extremely extended.

First, the possibility to rapidly transform such

insulating materials into plasmas within 10

-15

second

timescale and on micrometric dimensions is of

strong interest for a vast panel of future ultrafast

applications (Sugioka and Cheng, 2013): change of

electrical properties for ultrafast laser-induced

electronic switches, change of optical properties for

ultrafast plasma mirrors and plasma optics, structural

change of atomic lattice (ultrafast melting) enabling

to change the refractive index, etc. Second, for

intensities above the material ablation threshold, the

final result is highly interesting for material

processing at micro- and nano-scales: voids for

memories, channels for microfluidic,

ophthalmic/neuronal surgery, material cutting,

drilling, surface structuration (e.g. for metamaterials

or plasmonics), etc. All these cutting-edge

applications for future technology and industry are

based on ultrafast laser-induced ionization of

dielectric solids, which provides time- and space-

confinement of energy for matter transformation.

Even for ablation, for which several temporal

orders of magnitude separate the very first stage of

interaction (ionization) and the removal of matter

produced by one single pulse, experimental

observations establish that the result of ablation is

closely linked to and driven by the mechanisms and

the dynamics of absorption (Balling and Schou,

2013). Yet, it turns out that for material ablation, the

total amount of energy that is deposited in the

material is of highest importance, since part of the

interacting energy is not optimally used for ablation

and is finally relaxed into unwanted effects in the

material (recast products, rims, thermal load,

residual mechanical constraints, etc.) (Ben-Yakar et

al., 2007). Although these effects are reduced in the

femtosecond pulse regime compared to longer pulse

durations, they are nevertheless no more negligible

when dealing with the micrometer scale. For the best

control of the outcome of ablation, it is therefore

important to provide no more than the amount of

laser energy necessary to machine the calibrated

modiﬁcation of the material surface.

Sanner, N., Lebugle, M., Varkentina, N., Sentis, M. and Utéza, O.

Optimizing Energy Absorption for Ultrashort Pulse Laser Ablation of Fused Silica.

DOI: 10.5220/0005685300690073

In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 71-75

ISBN: 978-989-758-174-8

In this context, it is important to precisely know

the response of the material, both temporally and

under various intensities of irradiation, to optimize

the result of ablation. Dielectric materials being

initially transparent to near infrared laser light, non-

linear absorption mechanisms are required to bridge

the band gap and promote free electrons in the

conduction band (Stuart et al., 1996). These seed

electrons are further accelerated through inverse

Bremsstrahlung (IB) and multiplied by impact

ionization (II) if their kinetic energy is sufﬁcient,

leading to an avalanche multiplication phenomenon.

Strong laser absorption therefore takes place in the

ﬁrst (hundred) nanometers at the surface of the

material, where the material has been turned opaque.

It may yield to damage or ablation of the material, if

the quantity of laser energy absorbed by the material

is sufﬁciently high and properly adjusted (Jia et al.,

2004, Chimier et al., 2011). At densities higher than

the critical plasma density, the material optical

properties evolve during the laser pulse, thereby

yielding a feedback on the dynamics of absorption

(Chowdhury et al., 2005, Hernandez-Rueda et al.,

2012) and consequently on the amount of energy

that is absorbed. This actually depends on the

characteristics of the plasma layer which is created

at the surface of the sample by the pulse itself.

To explore this, we present here a complete

investigation of energy absorption, by combining

“pump-probe” (Lebugle et al., 2014) and “pump

depletion” (Varkentina et al., 2013) experiments in a

wide range of incident fluences above the ablation

threshold. The first offers the ability to follow in

time the free-electrons plasma buildup and its

transient optical properties, while the latter provides

information concerning the absorbed energy. This

extensive information finally provides a

comprehensive picture of material response and

strategies for optimizing the amount of energy that is

eventually deposited in the material.

2 DYNAMICS OF ABSORPTION

2.1 Setup and Determination of Time

Zero

In order to probe the absorption during the

irradiating pulse, and therefore provide insights into

the mechanisms and dynamics of absorption, two

main conditions must be fulfilled (Lebugle et al.,

2015):

(i) Use a probe pulse much shorter than the pump,

to obtain high temporal sampling

(ii) Accurately determine the ‘time zero’, i.e. the

zero-delay instant between the peaks of the pump

and the probe pulses.

To address the first condition, we use a 500-fs pump

pulse, delivered by a commercial source (emitting at

1025 nm) and a 60-fs probe pulse at the same

wavelength, issued from self-phase modulation in a

microstructured fiber and further compressed by

chirped mirrors. The probe pulse duration is

therefore a factor of eight shorter than the pump

pulse, thus allowing accurate temporal sampling of

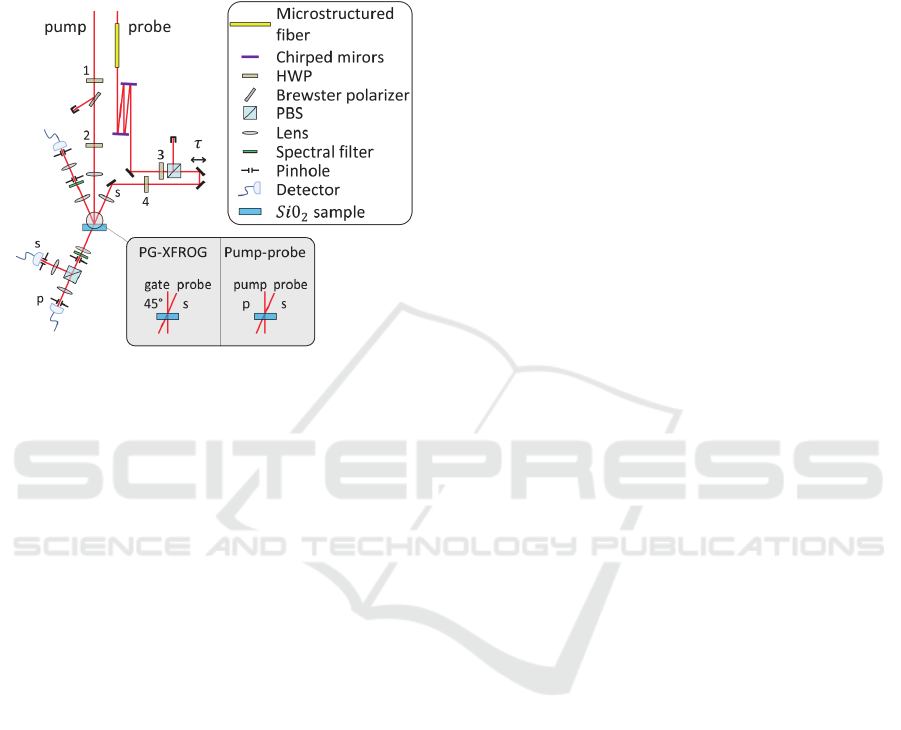
the optical transient states. The experimental setup is

sketched in Figure 1. The pump beam is focused

with normal incidence at the surface of the SiO

sample with horizontal polarization, and probed by

the s-polarized pulse at an angle of 20°. The two

beams are carefully mode-matched, with radii of ~13

µm at 1/e² in intensity, measured by imaging of the

beams onto a CCD camera with adapted

magnification. The reﬂected and transmitted parts of

the probe pulse are recorded by photodiodes after

spectral, spatial (lens and pinhole) and polarization

ﬁltering.

The second condition is of highest importance to

retrieve the exact temporal dynamics of mechanisms

involved in the interaction at the timescale of the

pulse. Instead of using nonlinear crystal in place of

the SiO

sample to perform SHG or THG for

determining the ‘time zero’, we directly rely on the

nonlinear second order coefficient of fused silica

itself (



310



²/). This offers the

advantage to work directly in-situ, and suppresses

the difﬁculty to further position the surface of the

target material exactly in the same plane as the non-

linear crystal used once it has been removed. This

configuration is in fact a polarization-gated cross-

correlation FROG experiment (PG-XFROG). It

enables to characterize in situ the probe pulse

(intensity and phase), but more importantly to

accurately calibrate the temporal overlap between

the pump and probe pulses. For that, the polarization

of the pump pulse is set to be 45° with respect to that

of the probe one, and the photodiode monitoring the

p-component of the polarization of the probe pulse is

also replaced by a spectrometer. Upon irradiation by

a low-energy pump pulse, transient birefringence

appears inside the fused silica sample during the

pump pulse, so that the polarization of the probe

beam is slightly turned to allow spectral analysis by

the spectrometer of the signal coming through the p-

transmitting polarizing beam-splitter. By time

delaying the probe pulse with respect to the pump

pulse, the spectrally resolved PG-XFROG signal is

recorded. We finally retrieve the probe pulse

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

duration of 60 fs, in excellent agreement with

independent measurement performed with a second-

order autocorrelator. More importantly, the zero-

time delay is deﬁned by the instant of superposition

of the peaks of the pump and probe pulses, with a

precision of ± 30 fs.

Figure 1: Experimental set-up. A 500-fs pulse is split into

two arms, and the probe pulse is further compressed down

to 60 fs using spectral broadening in a micro-structured

ﬁbre, with the second-order spectral phase adjusted with a

pair of chirped mirrors. The two pulses are then focused

on the surface of the fused silica target, controlling the

delay between them. This pump–probe set-up, which is

designed to measure the optical dynamics during laser

excitation, makes also possible the direct calibration of the

time zero in a PG-XFROG conﬁguration as well as

measuring the probe pulse (intensity and phase), provided

that the polarizations are properly set (see insets).

2.2 Dynamics of Transient Absorption

Now turning back to pump-probe experimental

configuration, transient optical properties of the

fused silica sample that transforms into plasma

during the pump pulse are measured as a function of

time delay for a set of increasing ﬂuences. Note that

these experiments are performed in single pulse

regime. Moreover, although the peak powers

attained with the highest fluences used here (~60

MW) largely exceed the critical power for self-

focusing in the fused silica sample (~3 MW at this

wavelength), in our experiments we do not detect

any signs of sub-surface or bulk laser-induced

damage.

For pump ﬂuences below the ablation threshold





5.8/², no signiﬁcant variations of the

probe signals are recorded, whereas for all ﬂuences

higher than the ablation threshold the plasma

properties strongly evolve during the pulse. Note

that we use a low-intensity probe pulse, whose

intensity (



210



/²) is well below

any material modiﬁcation threshold for a 60 fs pulse.

Indeed, we veriﬁed that no depletion of the probe

pulse occurs when the pump beam is blocked. We

also experimentally checked that no change is

observable in the response of the plasma as a

function of the probe energy. Thus, the plasma

absorption read by the probe mainly corresponds to

absorption by IB, i.e. the heating of the free carriers

(produced by the pump pulse) through collisions of a

photon with an electron in the ﬁeld of the parent

atom. The magnitude of this one-photon absorption

of the probe is then directly representative of the free

electron density of the plasma.

Transient transmissivity  and reﬂectivity 

recorded during the pulse are shown in Figure 2. A

large set of ﬂuences is explored, from 0.7



3.9



. All the curves show absolute values, so that

their initial values measured before the pump pulse

account for Fresnel reﬂection. With these

measurements, absorptivity can be deduced using

the energy conservation law:   1    .

Temporally, the curves present swift changes in

the second half of the pump pulse. They saturate

after the pulse at a time delay around 0.5 ps for all

ﬂuences. Concerning the reflectivity , we observe

that a plasma mirror effect occurs during the pulse,

and therefore partially limits energy deposition. This

evidences the formation of a transient overdense

plasma during the excitation pulse.

Now concerning absorption and its transient

dynamics, instantaneous absorption is maximal at

the end of the pulse (delay of ~500 fs). Transient

plasma absorption is higher and starts earlier (before

pump maximum) for growing fluences. At this point,

it is important to recall that what is measured is the

absorption of the probe pulse by Inverse

Bremsstrahlung (IB) at 1025 nm, meaning that the

probe pulse “reads” the plasma absorption

properties. Yet, since the probe and pump pulses

have the same wavelength and same spot size, this

demonstrates that IB absorption of the pump pulse

itself has a growing contribution during the second

half of the pulse, beginning earlier and earlier upon

increase of the fluence. The magnitude of IB

absorption reaches 40% for the highest fluence

3.9



, which is an indication that the predominant

mechanism of pump absorption is impact ionization.

However, we must remind that this is a mean value,

averaged on the whole spatial extend of the 2D

Gaussian beam profile. Thus, this effect should be

much more pronounced at the center of the beam.

Finally, these combined observations of R and T

Optimizing Energy Absorption for Ultrashort Pulse Laser Ablation of Fused Silica

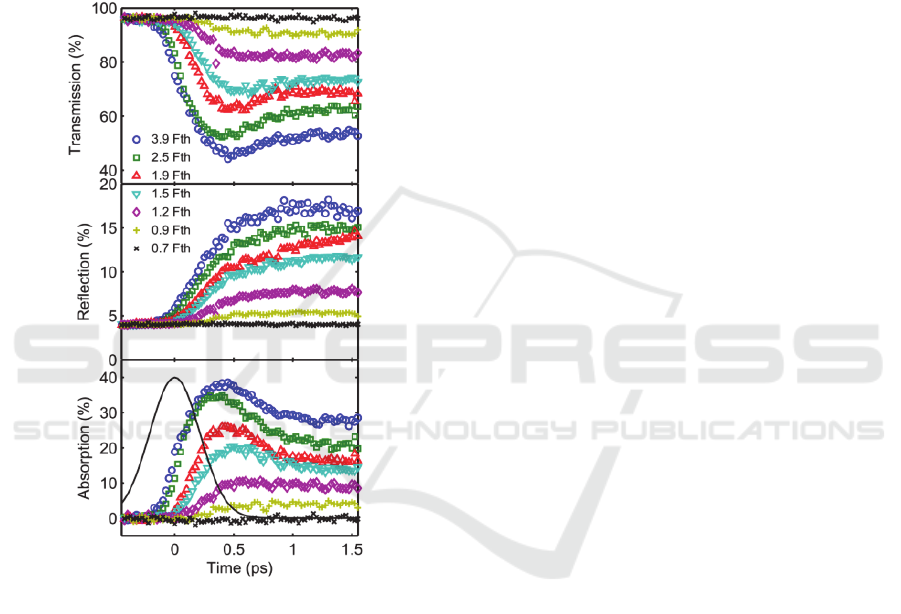
suggest the existence of a ﬂuence range that may

enable to maximize the transfer of energy from the

laser pulse to the material. Ideally, overall

reflectivity should keep moderate, together with high

level of absorption. In this perspective, it is

interesting to point out the saturation of absorptivity

when fluence increases. Indeed, only a small

variation is recorded between the curves for 2.5



and 3.9



. This is analyzed with respect to

integrated measurements in the next section, in order

to identify the optimal fluence range for ablation.

Figure 2: Transient optical properties of the fused silica

sample during the pulse (retrieved from pump-probe

experiments). Each data point is the average of 5

independent measurements. The pump pulse is also

represented with a Gaussian function of 500 fs duration

FWHM (arbitrary vertical units).

3 EFFICIENCY OF ABSORPTION

FOR ABLATION

With the aim to link absorption with ablation, we

also implemented a “pump-depletion” experiment.

In a complementary manner with the pump-probe

experiment, we thus explore the total absorption of

the pump beam, temporally integrated over the

whole pulse length.

This setup uses the same kind of experimental

arrangement as presented in Figure 1, but only the

pump pulse is present. The same incident laser beam

is focused on the sample surface, but here the beam

radius is smaller than in the previously presented

experiment (6.3 µm at 1/e²). However, the measured

fluence for ablation threshold is identical, making

therefore possible to compare directly these two

experiments. The transmitted and reflected fractions

of the incident pump pulse are measured with proper

photodiodes and filtering. Note that here these

signals are integrated both spatially (over the

radially Gaussian beam distribution) and temporally

(over the whole pulse length).

Post-mortem analyses of the ablated craters are

performed by atomic force microscopy, and we

define the absorption efficiency





as the ratio of

the ablated volume V to the absorbed pulse energy:





/



. Note that this quantity is different

from the usual ablation efficiency used in other

works (Utéza et al., 2011) based on incident rather

than absorbed energy. Figure 3 shows that the laser

energy is more and more efficiently absorbed for

growing fluences, until the curve reaches a plateau

(~0.65 µm

/µJ) followed by a slow decrease. This

saturation appears for fluences that are well in

accordance with the saturation of absorption

measured in the in the previous section, i.e. for

fluences around three times the ablation threshold.

A fluence range ΔF

eff,abs

corresponding to

efficient absorption for ablation can be interestingly

identified. Its limits are defined with respect to the

fluences yielding ~90% of the maximum absorption

efficiency. According to that criterion, the

absorption is efficient from ~2 to ~8



. It is

important to determine the range of ΔF

eff,abs

when

one is intended to develop micromachining

applications. Indeed, it helps to define an optimal

working fluence range, where maximal absorption is

attained and the energy deposition is not too strongly

disturbed by the plasma screening effect. From the

viewpoint of efficient material removal, reaching

this precise state of the material optimizes

absorption efficiency, i.e. enables the optimal

utilization of photons for material ablation.

Moreover, the best ablation quality is also obtained

for fluence values corresponding to the ΔF

eff,abs

range, as illustrated by the typical crater morphology

displayed on figure 3 (corresponding to 3.9



Below 2



, the energy is not sufficient to produce a

smooth ablation (high surface roughness), and above

8



we observe a higher level of debris and a lower

efficiency removal, which is often not suitable for

applications.

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

Figure 3: Absorption efﬁciency 



/



, as a

function of normalized laser ﬂuence. ΔF

eff,abs

determines a

ﬂuence zone of high efﬁciency of absorption, by taking a

criterion of 90% of the maximum value. For illustration,

an AFM picture of a typical crater obtained in this range is

shown (corresponding here to 3.9



, with a crater

diameter of 9.3 µm and a maximum depth of 210 nm).

4 CONCLUSIONS

In conclusion, the dynamics of transient optical

properties of silica during a 500-fs laser pulse is

retrieved and compared to time-integrated ones,

obtained by independent energy balance

measurement. The high temporal resolution

achieved in this experiment enables to reveal the

fine dynamics of transient material states. In

particular, for ablation purposes, it appears that an

optimal fluence range (with respect to ablation

efficiency) is identified between two and four times

the ablation threshold. This corresponds to a very

particular situation: the material has already turned

strongly absorbing, whereas its reflective properties

are still low. This is taking place mostly in the

second half of the pulse. In this regime, the incident

laser energy is best absorbed.

By demonstrating that a careful choice of the

incident fluence promotes a large coupling of the

incoming laser energy to the excited material, this

work is of particular importance in the context of

micromachining process, for which a better control

of the material excitation is sought. Our results

highlight the crucial role of transient optical

properties during the laser-matter interaction in the

regime of ablation, and open a comprehensive way

toward designing dedicated user-defined temporal

excitation profiles.

ACKNOWLEDGEMENTS

Financial support of the French National Agency of

Research (ANR) - Nanomorphing-07-BLAN-0301-

03 and the Region Provence-Alpes-Côte d’Azur and

Department of Bouches-du-Rhône is gratefully

acknowledged.

REFERENCES

Gamaly, E., 2011. Femtosecond laser-matter interactions.

Pan Stanford Publishing.

Sugioka, K., Cheng, Y., 2013. Ultrafast Laser Processing:

From Micro- to Nanoscale, Pan Stanford Publishing.

Balling, P., Schou, J., 2013. Femtosecond-laser ablation

dynamics of dielectrics: basics and applications for

thin ﬁlms. Rep. Prog. Phys. 76 036502.

Ben-Yakar, A., Harkin, A., Ashmore, J., Byer, R.L.,

Stone, H.A., 2007. Thermal and ﬂuid processes of a

thin melt zone during femtosecond laser ablation of

glass: the formation of rims by single laser pulses. J.

Phys. D: Appl. Phys. 40 1447–1459.

Stuart, B.C., Feit, M.D., Herman, S., Rubenchik, A.M.,

Shore, B.W., and Perry, M.D., 1996. Nanosecond-to-

femtosecond laser-induced breakdown in dielectrics.

Phys. Rev. B 53, 1749.

Jia, T., Xu, Z., Li, R., Feng, D., Li, X., Cheng, C., Sun, H.,

Xu, N., and Wang, H., 2004. Mechanisms in fs-laser

ablation in fused silica J. Appl. Phys. 95(9), 5166.

Chimier, B., Utéza, O., Sanner, N., Sentis, M., Itina, T.,

Lassonde, P., Légaré, F., Vidal, F. and Kieffer, J.C..

2011. Damage and ablation thresholds of fused-silica

in femtosecond regime Phys. Rev. B 84, 094104.

Chowdhury, I.H., Wu, A.Q., Xu, X., and Weiner, A.M.

2005. Ultra-fast laser absorption and ablation

dynamics in wide-band-gap dielectrics Appl. Phys. A

81, 1627.

Hernandez-Rueda, J., Puerto, D., Siegel, J., Galvan-Sosa,

M., and Solis, J. 2012 Plasma dynamics and structural

modiﬁcations induced by femtosecond laser pulses in

quartz Appl. Surf. Sci. 258(23), 9389.

Lebugle, M., Sanner, N., Varkentina, N., Sentis, M., and

Utéza, O. 2014 Dynamics of femtosecond laser

absorption of fused silica in the ablation regime J.

Appl. Phys. 116, 063105.

Varkentina, N., Sanner, N., Lebugle, M., Sentis, M., and

Utéza, O. 2013 Absorption of a single 500fs laser

pulse at the surface of fused silica: Energy balance and

ablation efficiency J. Appl. Phys. 114, 173105.

Lebugle, M., Utéza, O., Sentis, M., and Sanner, N. 2015

High temporal resolution and calibration in pump–

probe experiments characterizing femtosecond laser–

dielectrics interaction, Appl. Phys. A 120, 455–461.

Utéza, O., Sanner, N., Chimier, B., Brocas, A.,

Varkentina, N., Sentis, M., Lassonde, P., Légaré, F.

and Kieffer. 2011 Control of material removal of fused

silica with single pulses of few optical cycles to sub-

picosecond duration Appl. Phys. A 105, 131.

Optimizing Energy Absorption for Ultrashort Pulse Laser Ablation of Fused Silica